第二类曲面积分的算法研究

汪 叶 范利萍

河南大学数学与统计学院 河南开封 475001

一、概述

高等数学是高等院校非数学专业学生必修的一门公共基础课程，其主要内容是一元函数和多元函数微积分学。多元函数积分学包含了二重积分、三重积分、两类曲线积分和两类曲面积分等六种积分。其中，第二类曲面积分是多元函数积分学教学内容体系中的最后一个积分，是教学的重点和难点。经历了前面五种积分的学习，再加上第二类曲面积分的概念、定理和公式的抽象性，导致部分学生思路混乱，产生畏难情绪。第二类曲面积分的题目综合性强，难度高，方法多变，计算过程复杂而冗长，学生不易掌握。因此，教师要逐步引导学生思考和探索第二类曲面积分不同题型对应的计算方法，鼓励学生及时总结，帮助学生理解和掌握第二类曲面积分的相关知识，提高学生分析和解决问题的能力，培养学生的创新能力。

二、第二类曲面积分的算法

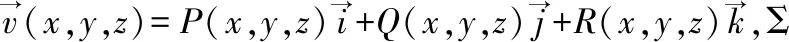
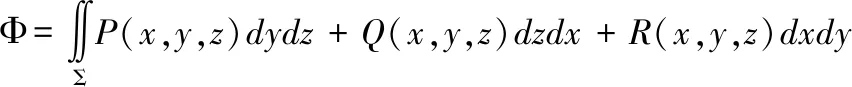
其中，dydz、dzdx和dxdy称为投影元素。要想灵活掌握第二类曲面积分的计算方法，除了深入理解其物理背景和概念之外，还要熟练掌握其性质，例如，利用对称性和奇偶性、轮换对称性[4-5]简化计算，同时要熟悉与高斯公式有关的各种题型。下面主要探讨第二类曲面积分的算法。

(一)直接投影法

当积分的被积表达式中只有一个投影元素时，采用直接投影法将第二类曲面积分转化为二重积分计算。计算口诀是：一投、二代、三定号。一投指根据投影元素确定将曲面Σ投影到哪个坐标面上；二代指将曲面的方程代入被积函数；三定号指由曲面的侧决定二重积分的符号。例如，当被积表达式中含有投影元素dxdy时，首先将曲面Σ往xOy面上投影得到投影区域Dxy，然后将曲面方程z=z(x，y)代入被积函数，最后由曲面的侧判定二重积分的符号，上侧为正，下侧为负。其他两种情形类似可得，这里不再赘述。

例1 设Σ是球面x2+y2+(z-a)2=a2的外侧，计算曲面积分Σz2dxdy。

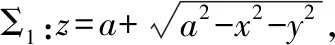
(二)二化一法

当Σ是一张平面时，法向量是常向量，此时利用两类曲面积分之间的联系将第二类曲面积分转化为第一类曲面积分计算更为简便，该方法称为二化一法。公式如下：

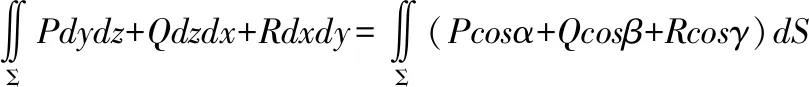
(1)

其中，cosα、cosβ和cosγ是有向曲面Σ在点(x，y，z)处的法向量的方向余弦。

例2 计算曲面积分∬Σxzeydydz-xzeydzdx+zdxdy，其中Σ是平面x+y+z=1在第一卦限部分的上侧。

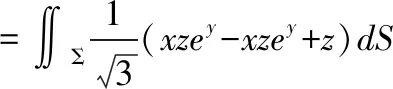
(三)合一法

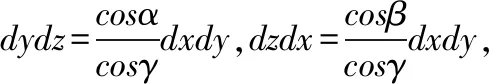
(2)

例3 计算曲面积分∬Σxdydz+ydzdx+zdxdy，其中Σ是曲面z=x2+y2，0≤z≤1在第一卦限部分的上侧。

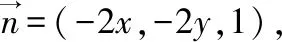
原式=∬Σ[x·(-2x)+y·(-2y)+z]dxdy

=∬Dxy(-x2-y2)dxdy

(四)利用高斯公式将其化为三重积分

当Σ是一张封闭曲面时，可以通过高斯公式将第二类曲面积分转化为三重积分计算。高斯公式如下

(3)

解：由高斯公式:

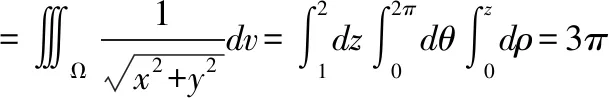
(五)补面法

当积分的被积表达式很复杂，且Σ不是封闭曲面时，不能使用方法一直接投影法，也不能使用高斯公式(因为不满足高斯公式的封闭性)，怎么办呢？联想到格林公式[1]存在类似的问题：当曲线不闭合但还想使用格林公式时，怎么处理呢？解决方法是添加辅助曲线使之闭合后再用格林公式。类似地，这里可以添加辅助曲面使之封闭后再用高斯公式，即补面法。一般地，优先添加平行于坐标面的平面。注意，补面时需要标注曲面的侧。

例5 计算曲面积分

∬Σ(x-1)3dydz+(y-1)3dzdx+(z-1)dxdy

其中Σ是曲面z=x2+y2，0≤z≤1的上侧。

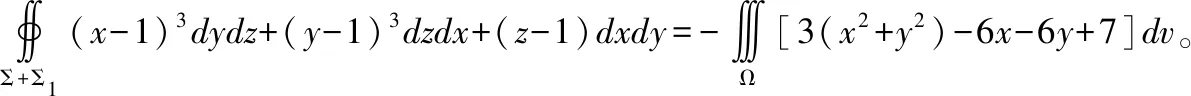
显然有∬Σ1(x-1)3dydz+(y-1)3dzdx+(z-1)dxdy=0。而由对称性和奇偶性可得∭Ω(6x+6y)dv=0。然后采用柱面坐标法计算三重积分，得到：

原式=-∭Ω[3(x2+y2)+7]dv

=-4π

(六)“挖洞”法

当空间闭区域Ω上存在奇点时，高斯公式的第三个条件不满足，怎么办呢？再次联想到格林公式[1]的类似情形，是采用“挖洞”的方法解决的。于是，这里也可以采用“挖洞”的方法将奇点挖去，然后在复连通区域上使用高斯公式。注意复连通区域有两个边界曲面，外边界曲面的侧应取为外侧，内边界曲面的侧应取为内侧。

例6 设Σ是一张不经过点M0(x0，y0，z0)的光滑闭曲面，侧取外侧，计算曲面积分。

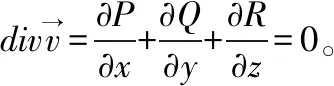
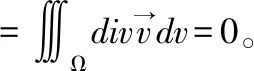
情形2：当M0(x0，y0，z0)∈Ω时，M0是奇点。以M0为中心，以r为半径做小球面Σ1：(x-x0)2+(y-y0)2+(z-z0)2=r2，取内侧。注意r要足够小，使得Σ1包含在Σ内。记Σ和Σ1围成的空间复连通区域为Ω1，Ω1上无奇点，可以使用高斯公式，得到：

故有：

记Σ1围成的小球体为Ω2，在上式的曲面积分中被积函数P=x-x0，Q=y-y0，R=z-z0在Ω2上无奇点，可以再次使用高斯公式。注意曲面Σ1的侧是内侧，于是有：

故，原式=4π。

结语

本文通过实例分析，探讨了第二类曲面积分的六种典型题型和相应的计算方法，加深了学生对该知识点的理解。在教学中，教师要循序渐进地引导学生思考，提高学生化未知为已知的能力，提升学生运用已学知识分析问题和解决问题的能力，培养学生的创新意识。同时，学生在学习时要进行大量的练习，这样才能拥有较强的运算能力、严密的逻辑推理能力，最终达到“运用之妙，存乎一心”的境界。