基于强度折减法判断圆形隧洞围岩稳定性研究
杜怡谦,李美香,何 宁,3,周彦章,3,佘义邦,马昕玥
(1.南京水利科学研究院岩土工程研究所,江苏 南京 210029;2.南京市江宁区水务局,江苏 南京 211112;3.水利部水库大坝安全重点实验室,江苏 南京 210029)
跨区域引调水工程是实现区域水资源优化配置、解决水资源时空分布不均问题和强化供水安全保障的重大战略举措,长距离输水隧洞是实现跨区域引调水工程的重要手段。然而,长距离输水隧洞大多要穿越地质条件复杂的地区,且单洞长、埋深大,不利因素众多,如南京市江宁区新济洲供水工程过江段输水隧洞下穿长江、上覆深厚软土/风化岩地层,采用单层衬砌的盾构法施工,隧洞围岩稳定性判断研究对于工程安全实施运行至关重要,也是亟待解决的科学技术难题。
隧洞开挖后其结构的稳定性主要取决于围岩自身的稳定性,因此隧洞围岩的稳定性是隧洞设计、施工的关键问题[1]。但是,对隧洞围岩的稳定性评价一直缺乏一个合理的评判指标,传统的极限分析法虽然简单易用,但是对岩土体材料的力学性质做了大量简化,如不考虑岩土体本构关系,只考虑材料为均质情况等[2];而传统的有限元法虽然适用性比极限分析法广,但它无法计算出隧洞的极限荷载、安全系数和围岩破坏面,仅凭应力、位移、拉应力区和塑性区很难确定隧洞的安全度与破坏面[3]。为了克服上述两种方法的缺点,极限分析有限元法应运而生,形成一门新的学问。它使极限分析可以由数值分析方法运算,并有现成程序可用,从而扩大了极限分析法的应用范围,同时,也使得有限元法能够直接计算极限荷载与安全系数,并确定破坏面,增加了这一方法的功能。目前公认的最早提出极限分析有限元法的是英国学者Zienkiewicz等[4],认为可以通过增加外荷载或降低岩土强度的方法来计算岩土工程的安全系数。其中,通过对岩土体强度参数的折减,使岩土体处于极限状态的方法也被称作强度折减法,而这种方法在边坡稳定分析中应用颇多。国内学者张黎明等[3]首先尝试了将强度折减法应用于求解隧洞的稳定安全系数中。最初,强度折减法仅用于线性Mohr-Coulomb准则,后推广到非线性强度模型,如Hoek-Brown准则中。
基于此,本文介绍了2种基于广义Hoek-Brown准则的强度折减方法,应用有限差分强度折减法,以某一输水隧洞顶部竖向位移发生突变作为失稳判据,利用FLAC3D软件计算其安全系数,并将其与通过Mohr-Coulomb准则计算得到的结果进行对比,确定其合理性。
1 基于广义Hoek-Brown准则的强度折减方法
1.1 Hoek-Brown准则基本理论
Hoek等[5]认为,岩石破坏判据不仅要与实验结果吻合,其数学表达式也应尽可能简单,并且岩石破坏判据不仅要适用于结构完整且各向同性的理想均质岩体,还要适用于碎裂岩体以及各向异性的非均质岩体,因此,Hoek等[5]通过对大量岩石的破坏包络线进行系统研究,统计分析之后得到了狭义Hoek-Brown经验准则:
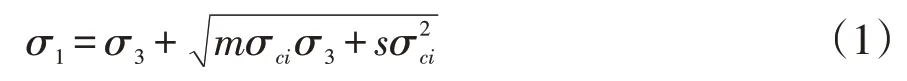
式中:σ1为岩体破坏时的最大主应力;σ3为作用在岩体上的最小主应力;σci为完整岩石单轴抗压强度;m和s为经验参数,m反映岩石的软硬程度,s反映岩体的破碎程度,可由岩体的RMR分值确定。
随着岩土工程的快速发展,基于RMR值的狭义公式经过多次改进、修正,逐渐发展成如下广义形式[6]:
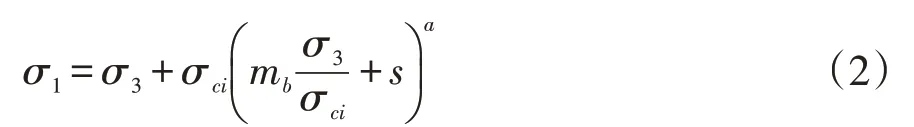
式中:mb,s,a均为刻画岩体特性的半经验参数,并且都可表示为经验参数GSI的函数:
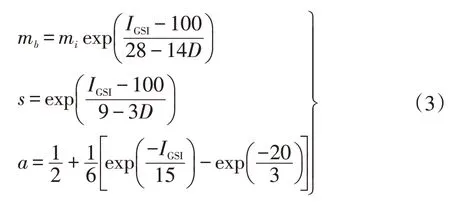
式中:mi为材料常数,由完整岩石三轴压缩试验得出;D(0~1)为考虑工程扰动因素的岩体弱化因子;IGSI为GSI值,根据工程岩体的岩体结构、结构面特征(粗糙度、风化程度、填充物状况等)由经验综合确定[6]。
3.2 基于广义Hoek-Brown准则的强度折减法
现有的强度折减法主要基于Mohr-Coulomb准则实施。假设岩土体处于原始状态时,其内黏聚力为c,内摩擦角为ϕ。当折减系数为K时,折减后参数Ccr,以如下方式计算:

当K=F(F为岩土体的安全系数)时,岩土体达到临界失稳状态。
李远耀等[7]提出,与Mohr-Coulomb准则强度折减法的一致性和能否体现节理岩体的真实破坏特性,是评价Hoek-Brown准则强度折减法优劣的标准。其指出,广义Hoek-Brown准则实质上具有4个基本输入参数,σci、mi、GSI和D。其中D为工程扰动因子,和岩体强度本身无关,无需折减。因此,只需要考虑剩余3个参数如何折减。
对比σci、mi同比折减;σci、GSI同比折减;GSI、mi同比折减3种方法后,通过试算分析,得出第三种方法与Mohr-Coulomb准则强度折减法的等效性更好的结论(简称为HB-LYY法)。
任俊等[8]提出了一种针对抗剪强度的折减方法(简称HB-RJ法)。首先,根据Kumar[9]的研究,知道基于正应力和剪应力的Hoek-Brown准则有如下形式:

若对抗剪强度进行折减,折减系数为f,设则有(Scr、σcicr、mbcr为折减后的Hoek-Brown准则相关参数):
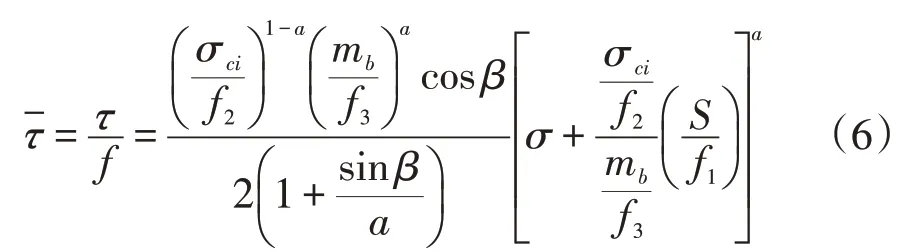
此时,可得f2=f3=f,f1=1。
2 围岩失稳判别方法
实施强度折减法的关键在于判断围岩是否达到了失稳状态,因此,需要首先确定围岩的失稳判据。目前数值计算中关于岩土工程的失稳判据主要有以下几种:
方法1:采用数值计算在规定迭代次数内不收敛;
方法2:以广义塑性应变或者广义剪应变发生整体性的贯通;
方法3:以特征点发生位移突变。
林杭等[10]采用了方法1,使用这种方法时,必须预先设定时步数,若在设定的时步数内数值计算能够收敛,那么就说明围岩没有达到极限状态,需要继续增加折减系数,反之,则说明此时折减系数过大,需要减小折减系数,如此反复便可得到一个安全系数的估计区间。但是,预先设定的时步次数具有很大的主观性,因而可能产生较大的人为误差。同理,方法2中采用的塑性区贯通的客观指标是很难确定的,目前只能通过观察者的主观认识来判断,人为因素的影响很大。
对于方法3,苏永华等[1]认为隧洞的拱顶下沉是实际工程中隧洞监测的必测项目,是围岩稳定性评价的关键变形控制变量,因而采用隧洞拱顶下沉发生突变作为隧洞发生破坏的判据。其实现方法是将不同折减系数条件下的隧洞拱顶沉降绘制成散点图,并用两条斜率不同的直线拟合突变前后两部分的数据,这两条直线的交点所对应的横坐标就是所求的安全系数。但是这种方法在界定突变前后的数据点范围时也有很大的主观性,而这又会造成两条拟合直线的交点发生变化,即安全系数的值会随主观判断的不同而产生差异。
针对这一问题,本文引入了滑动t-检验来确定突变点的位置。该方法常应用于气象学中,如检测气温突变、降水量突变等,其基本思想是把一组数据序列中两段子序列均值有无显著差异看为来自两个总体均值有无显著差异的问题来检验。如果两段子序列的均值差异超过了一定的显著性水平,可以认为均值发生了质变,即突变发生[11]。
滑动t-检验的实现方式说明:对具有n个样本量的顺序序列x,认为设置某一特定自变量值为基准点,基准点前后两段子序列x1和x2的样本分别为n1和n2,两段子序列平均值为x1和x2,方差为S21和定义统计量:
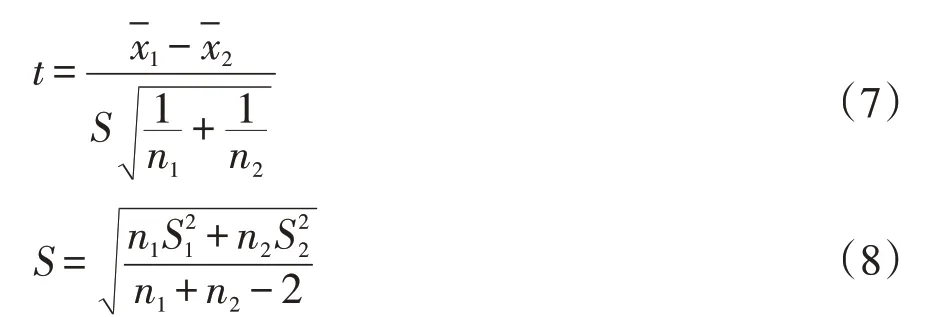
则式(7)遵从自由度v=n1+n2-2的t分布。那么通过滑动t-检验考察“隧洞拱顶沉降-折减系数”图象斜率的变化趋势,并找到斜率发生最明显变化的突变点,则“该点对应的折减系数RF值即为隧洞稳定安全系数值”这一假设为真的置信度最高。此方法降低了确定突变点时的主观因素影响,并且操作简单,逻辑清晰,便于计算机编程实现,提高了确定突变点时的可操作性。
3 算例与分析
为验证基于广义Hoek-Brown准则强度折减法的合理性,对比分析两种不同折减方法(HB-RJ法与HB-LYY法)的优劣,本文通过数值仿真软件FLAC3D进行模拟计算。并且,两种折减方法均采用相同模型和边界条件,只有参数折减方式的不同。
此外,为验证两种方法与基于Mohr-Coulomb准则的强度折减法的一致性,通过Hoek等[12]给出的换算公式,得到了等效的Mohr-Coulomb准则参数,并对其作折减计算作为参考(简称为等效M-C法)。
3.1 算例模型
为便于讨论,选取某一均质围岩深埋圆形输水隧洞作为分析对象,断面半径R=4 m,拱顶埋深H=40 m。计算时按照平面应变问题来处理,模型范围为底部及左右两侧各取五倍硐室跨度[13],向上取到地表,即宽×高=88 m×88 m;边界条件是左右两侧为水平约束,下部为固定约束,上部为自由边界(图1)。相关地质、物理力学参数分别为:重度γ=22 kN/m3,地质强度指标IGSI=45,mi=17,扰动因子D=0.7,完整岩石的单轴抗压强度σci=80 MPa。根据公式(3)即可得到围岩岩体广义Hoek-Brown准则的相关参数。同时,可根据广义Hoek-Brown准则计算岩体的等效Mohr-Coulomb准则抗剪强度参数:内粘聚力c与内摩擦角ϕ(表1)。

图1 计算模型

表1 模型相关参数
3.2 计算分析
分别按照HB-RJ法、HB-LYY法以及等效M-C法对上述模型进行强度折减计算。折减系数K的取值范围为1.0~2.0,步长为0.01,共计101次不同折减系数条件的仿真计算,收集整理每次计算完毕后隧洞拱顶的沉降值,以及对应的不同系数下拱顶沉降曲线斜率,并绘制成图2~3。
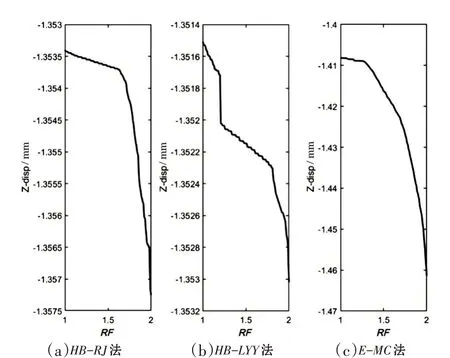
图2 不同折减系数下隧洞拱顶沉降
从图2可以看出,使用3种方法进行强度折减时,隧洞拱顶的竖向位移均出现了明显的突变现象;而从图3可以看出,在折减系数较小时,拱顶沉降曲线斜率能够保持稳定,当折减系数逐渐增大时,曲线斜率出现了明显的突变,说明拱顶沉降变化趋势从线性增大转变为快速地不受控增大。

图3 不同折减系数下隧洞拱顶沉降斜率
为确定发生突变的具体位置,通过滑动t-检验对3种方法的“折减系数-拱顶沉降曲线斜率”序列进行考察,具体步骤如下:
(1)确定基准点前后两子序列的长度,一般取相同长度,本文设置为n1=n2=10;
(2)采取滑动的方法连续设置基准点,依次按照计算统计量,可得统计量序列ti,i=1,2,…,n-(n1+n2)+1;
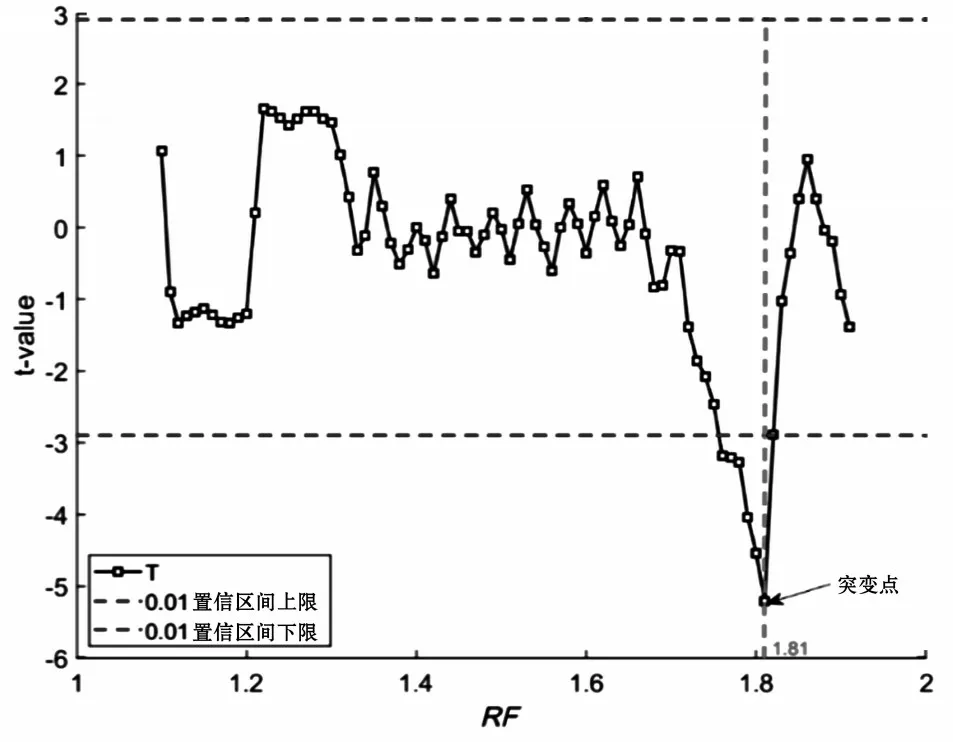
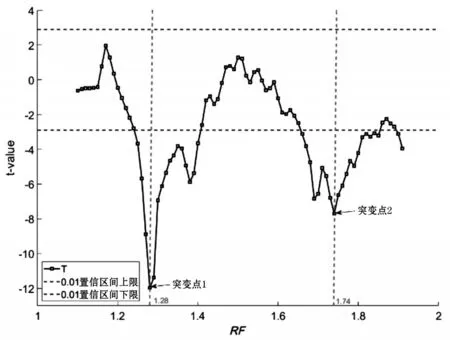
(3)给定显著性水平α,查t分布表得到临界值tα,若||ti (4)将计算得出的统计量序列ti与t0.01=±2.898绘制在同一坐标系中,如图4~图6所示; 图4 HB-RJ法下t统计量曲线 图5 HB-LYY法下t统计量曲线 图6 等效M-C法下t统计量曲线 (5)根据t统计量曲线上的点是否超过t0.01来判断拱顶沉降发生突变这一假设是否有足够的可信度。 从图4~6可以发现,HB-RJ法与HB-LYY法对应的t统计量曲线都呈现出了明显的“平缓-陡峭-平缓”趋势,这说明,在折减系数增大到某一范围时,拱顶沉降曲线斜率出现了剧烈的减小(说明拱顶沉降开始快速增加),导致前后两段子序列均值产生了显著差异。其中,在取折减系数RF=1.71与1.81时,t统计量分别取到了HB-RJ法与HB-LYY法下的最小值,即在此处,曲线斜率发生了最为明显的变化。因此可分别取2种方法对应的安全系数为FRJ=1.71与FLYY=1.81。而在等效M-C法对应的t统计量曲线则出现了2个不同峰值,对应的折减系数RF分别为1.28与1.74,即等效M-C法下的拱顶沉降曲线斜率发生了2次较为明显的变化。 结合图2中的曲线图可以发现,在1.28≤RF≤1.74时,虽然隧洞拱顶沉降趋势增大,但仍然保持着良好的线性,并且实际位移量也非常有限,与RF>1.74时曲线呈现的快速下降趋势有很大不同。此外,分析图6中的t统计量曲线也可以看出,在RF>1.74时,t统计量仍然保持在较低水平,这代表拱顶沉降曲线斜率仍保持快速下降趋势;相对1.28≤RF≤1.74时,t统计量在0附近上下波动,表明此时拱顶沉降曲线斜率没有明显变化。综上所述,取安全系数FEMC=1.74为宜。 对比3种不同方法得到的隧洞安全系数,彼此之间的相对误差如表2所示,可见3种方法得到的安全系数之间相差很小,最大相对误差也只有5%左右,显示出了很好的一致性。此外,对比结果说明HB-LYY法相较于HB-RJ法更为激进,在2种方法本身相对误差并不大的情况下,为保证隧洞结构稳定性有足够安全冗余,推荐选用HB-RJ法作为首选的强度折减法。 表2 安全系数相对误差 (1)基于强度折减法在广义Hoek-Brown准则中的实施,提出了圆形隧洞拱顶沉降发生突变的隧洞围岩失稳破坏判据,并且,通过引入滑动t-检验确定突变点位置,提高了计算隧洞稳定安全系数时的客观性和可操作性。 (2)采用3种不同折减方法,通过FLAC3D软件对同一算例进行计算,结果证明:3种方法得到的安全系数之间,相对误差很小,HB-RJ法、HB-LYY法与基于Mohr-Coulomb准则的强度折减法有很好的一致性,说明基于广义Hoek-Brown准则的强度折减法在圆形隧洞围岩的安全系数求解中是可行的。 (3)HB-RJ法相较于HB-LYY更加保守,在2种方法本身相对误差并不大的情况下,为保证隧洞结构稳定性有足够安全冗余,推荐选用HB-RJ法作为首选的强度折减方法。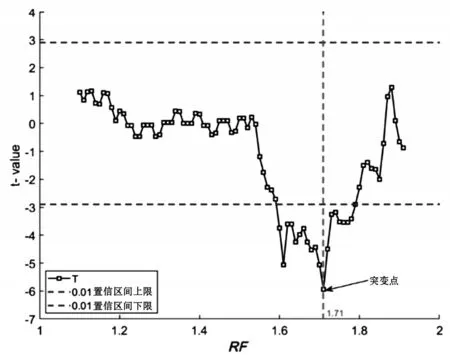

4 结论

