基于自编码器的多模态深度嵌入式聚类

徐慧英， 董仕豪， 朱信忠， 赵建民

(浙江师范大学 数学与计算机科学学院,浙江 金华 321004)

0 引 言

数据聚类的问题涉及场景十分广泛，包括深度学习、模式识别、图像处理及生物信息.聚类的目的是根据相似性度量(如欧氏距离)将相似数据分为一个类.科技的发展使数据收集变得更加方便，产生的数据维度也越来越高，数据间的相关性更加复杂.随着数据集变得越来越大和越来越多样化，需要对现有算法进行调整以保持聚类的质量和效率.传统的聚类算法由于数据维度不高，且为了能够获取所有的信息，所以会考虑数据的所有维度.但在高维数据中，数据的多个维度通常是不相关的，这些无关的维度会在嘈杂的数据中隐藏聚类，使得聚类算法混淆不清.在非常高维度的数据集中，所有对象彼此之间几乎等距，从而完全掩盖了聚类.特征选择方法已在某种程度上成功地用于改善聚类质量.近几年来，深度学习广泛的应用场景，如人工智能、智慧城市、联合医疗等，使得聚类分析有了新的发展空间.

自深度学习广泛且成功地应用以来[1-3]，自动学习最优表示已经成为主流，通过自动学习更好的特征表示在标准任务上获得了较好的结果.自动学习特征表示任务又被称为表示学习.更具体地说，表示学习是学习给定数据最显著特征的任务，即能表达数据底层结构的特征.它隐式地在有监督的深层神经网络中完成，通过使用其隐藏层来学习并为最后一层提供表示，从而使分类或回归等任务变得更加容易.例如，在原始特征空间中,线性不可分的数据点可以通过在隐藏层中的特征表示的组合在最后一个隐藏层处线性可分.因此，相对于特征工程，自动学习表示可以不受任务的影响，学习尽可能好的特征表示，以便在分类、聚类和回归等下游任务中获得更好的性能.为了进一步利用表示学习，可以显式地设计目标函数来学习有利于下游任务的表示，如聚类.深度嵌入聚类巧妙地将自编码器网络与聚类算法相结合，使用深度神经网络同时学习特征表示和聚类指派;变分深度嵌入算法是一种在变体自编码器框架内的无监督生成聚类方法，该模型使用高斯混合模型和深层神经网络对数据生成过程进行建模;生成对抗网络聚类[4]提出了使用生成对抗网络进行聚类的新机制，通过从单热点编码变量和连续潜变量的混合变量中采样潜变量，再加上结合聚类特定损失而训练的逆网络(将数据投射到潜空间)，能够在潜在空间中实现聚类；浅层深度聚类[5]使用浅层聚类算法而不是更深层的网络进行聚类，在原始数据和自动编码的嵌入方面研究了多种局部和全局流形学习方法；分离内部表示聚类[6]提出了一种更简单的方法来优化自编码器的参数学习及解除潜在编码表示的纠缠，将纠缠定义为来自相同类或结构的点对相对于来自不同类或结构的点对的接近程度；深度自监督聚类集成算法[7]首先根据基础聚类划分结果采用加权连通三元组算法计算样本之间的相似度矩阵，基于相似度矩阵表达邻接关系，然后将基础聚类由特征空间中的数据表示变换至图数据表示，在此基础上，将基础聚类的一致性集成问题转化为对基础聚类的图数据表示的聚类问题；深度多网络嵌入聚类[8]以端到端的方式预训练多个异构网络分支，获取各网络的初始化参数，在此基础上，定义多网络软分配，借助多网络辅助目标分布建立面向聚类的KL(Kullback-Leibler)散度损失，与此同时，利用样本重构损失对预训练阶段的解码网络进行微调，保留数据的局部结构性质，避免特征空间发生扭曲.通过随机梯度下降与反向传播优化重构损失与聚类损失的加权和，联合学习多网络表征及其簇分配.

与这些复杂的神经网络结构相比，本研究提出的结构利用自编码器学习数据的潜在表示形式，然后使用该形式进行聚类.本研究在对提取数据的潜在表示形式和融合方式上进行了创新.

1 基于自编码器的深度聚类

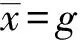
(1)

现有文献已提出了多种自编码器[9]，并应用于深度聚类中，主要改进集中在以下几个方面:

结构：原始的自编码器由多层神经元组成.当输入的数据是图像时，通常使用卷积神经网络构造的卷积自编码器来处理.

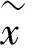
潜在特征的约束：欠完备自编码器(under-complete autoencoder)的潜在特征的维度小于输入样本的维度，能够有效提取原始数据的潜在特征.稀疏自编码器[11]能够施加稀疏约束.

2 基于自编码器的多模态深度嵌入式聚类模型

卷积网络对图像特征的提取明显要优于全连接网络，尽管已提出了残差神经网络用于提高多层卷积网络性能的方法,但多层卷积网络对于图像的整体特征及相关性的把握随着网络的加深却表现得不太理想.本研究通过多模态网络，寻求不同网络结构的相异性来提取相同数据的异向特征，用于提高网络提取图像全局特征与局部特征的能力.

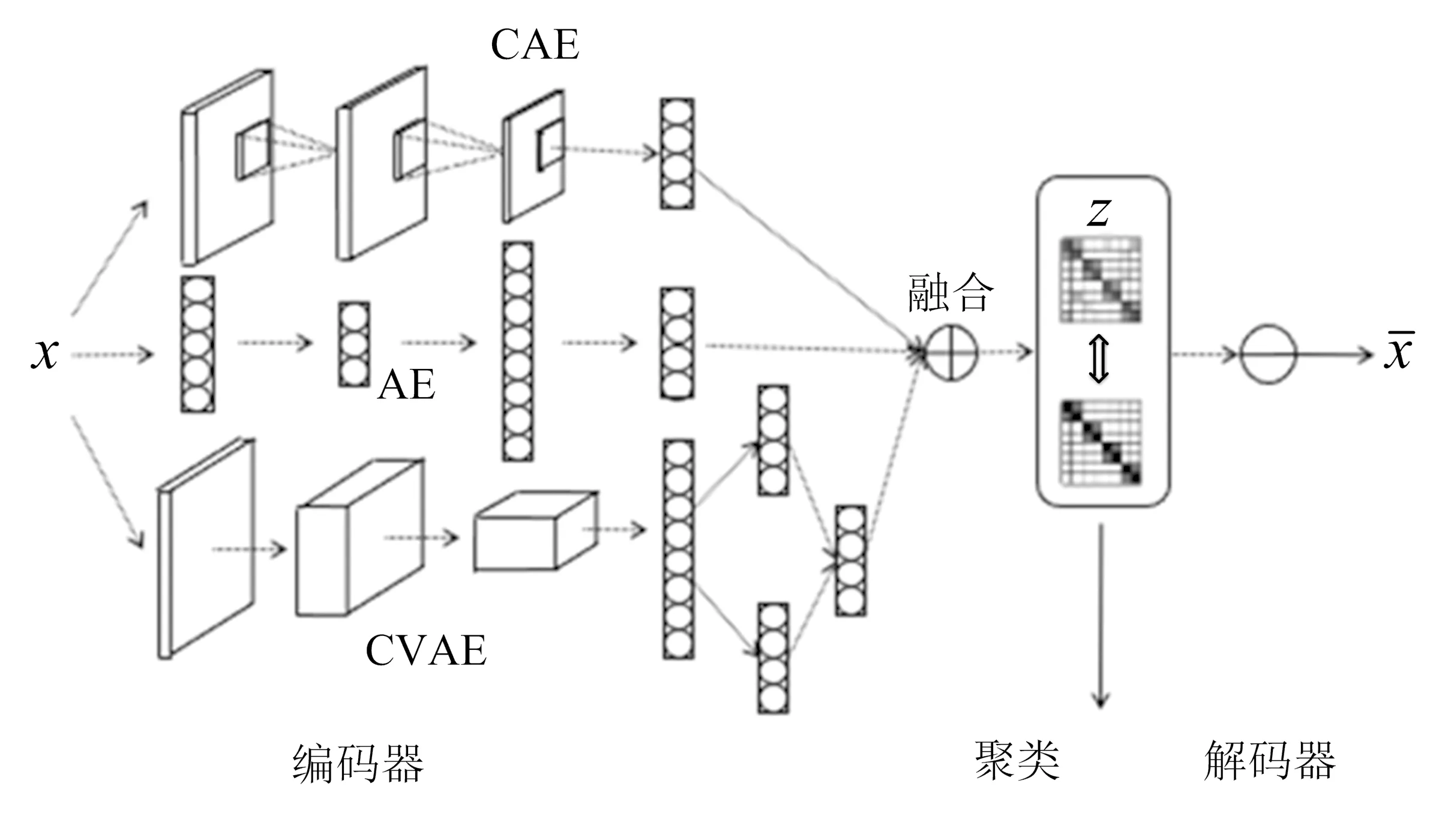
图1 基于自编码器的多模态深度嵌入式聚类结构

基于自编码器的多模态深度嵌入式模型(MDEC)的结构如图1所示，该结构由4部分组成：1)由自编码器(AE)、卷积自编码器(convolutional autoencoders,CAE)、卷积变分自编码器(convolutional variational autoencoder,CVAE)组成的编码器结构；2)多模态自适应融合层；3)深度嵌入式聚类层；4)解码器.

本研究设计的网络基于自编码器、卷积自编码器、变分自编码器这3种最有代表性的自编码器结构，并在此基础上结合深度子空间聚类结构组合而成.通过3种不同编码器获取原始数据的不同模态特征.3种特征存在相同和不同的信息，本研究的目的是将相同的特征信息合并，不同的特征信息相互补充，即多模态自适应融合，设置了融合重要性权重ω来表示3种子空间对融合子空间的不同贡献度，融合权重能通过网络迭代不断调整每个子空间的贡献度，使得融合后的子空间能更好地表征原始数据.将融合后的子空间特征输入深度聚类层得到最终的聚类结果.

2.1 模型定义

1)编码器

Zm=hm(X;θm),m=1,2,3.

(2)

2)多模态自适应融合层

为了获取原始数据更全面的信息，将不同自编码器获取的特征矩阵Zm通过自适应融合的方式进行融合，得到融合特征矩阵Z，对应的特征空间表示为Z，即

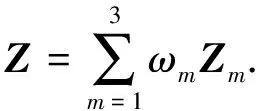
(3)

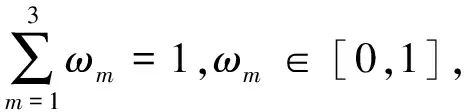
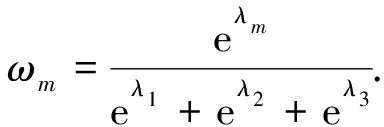
(4)

式(4)中：ωm分别通过使用λm作为控制参数的Softmax函数定义；λm作为可学习的参数，随机初始化后通过标准反向传播进行自动学习.

3)深度嵌入式聚类层

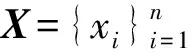
4)解码器

为了能更好地学习到原始数据的特征，本研究使用与编码器镜像对称的结构解码，即

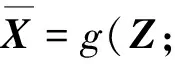
(5)

2.2 损失函数

损失函数由3部分组成：1)重构损失LR通过更新自编码器、卷积自编码器、卷积变分自编码器的网络参数来学习数据的低维嵌入特征；2)聚类损失LC通过更新聚类结果、自编码器参数和融合参数保证低维嵌入特征有利于聚类任务；3)融合损失LF通过更新融合参数ω使得各个模态的特征以最优的方式进行组合.整体损失函数如下：

L=LR+γLC+LF.

(6)

式(6)中，γ为聚类损失的权重系数.

1)重构损失

模型将编码器和解码器输出的平方差函数作为重构损失，一方面用于预训练自编码器，得到一个好的初始化模型;另一方面用于在聚类学习过程中保持数据的几何结构不变，则

(7)

2)聚类损失

使用学生T分布作为核函数计算特征点zi和聚类中心μj的相似度，即

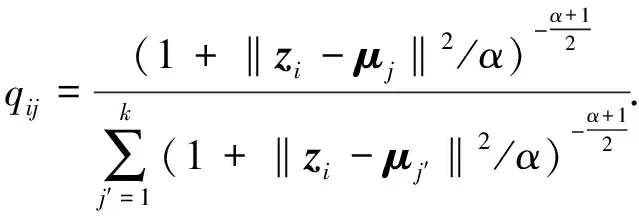
(8)

式(8)中：zi为样本xi的融合特征，即融合特征矩阵Z的第i行；α表示学生T分布[13]的自由度；qij表示第i个样本属于第j类的概率.本研究通过将软分配与目标分布相匹配来训练模型，损失函数定义为软分配qij和辅助目标分布pij之间的KL散度，即

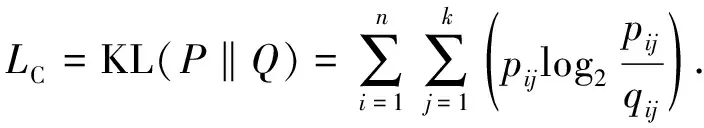
(9)

式(9)中：i=1,2,…,n;j=1,2,…,k;pij定义为

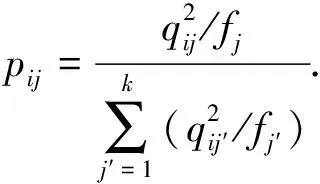
(10)

3)融合损失

从多个编码器获取的不同潜在特征Zm后，采用多模态融合的方法，将公共子空间特征与融合前的特征的平方差函数作为融合损失，使得公共子空间特征能最大限度地表示原始数据，定义为

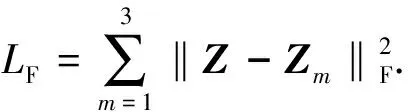
(11)

将训练分为2个阶段，分别是预训练初始化阶段和聚类优化阶段.在预训练初始化阶段，使用下面的损失函数训练模型：

L1=LR+LF.

(12)

聚类优化阶段使用下面的损失函数：

L2=LR+LF+γLC.

(13)

2.3 优化函数

通过带动量的随机梯度下降函数联合优化聚类中心μj和网络参数θ.损失函数关于每个数据点zi和类中心μj的梯度计算如下：

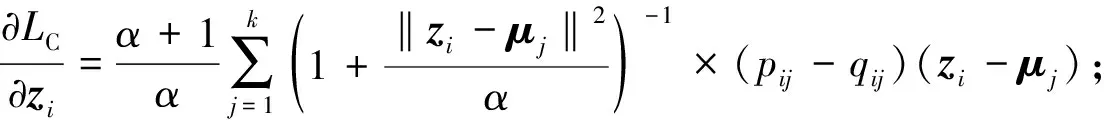
(14)

(15)

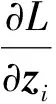
通过不同的编码器提取不同的潜在特征，并将特征融合到公共子空间中.经过预训练后，得到初始化的融合参数和模型参数，然后对融合后的公共子空间执行k-means聚类初始化聚类中心μj.

图2 数据集

3 实 验

实验均在深度学习GPU工作站上完成，工作站配置：CPU i7-9700k，GPU GeForce RTX 2080Ti.操作系统Ubuntu 18.04.5LTS，项目环境Python 3.6和TensorFlow 2.2.0框架来实现模型.设计了5次实验，最终实验结果通过去掉最高和最低的值并取平均，与经典算法和当前表现最好的、具有代表性的算法进行比较，验证本模型的有效性，并在4种公开数据集(见图2)上测试，详细数据集统计见表1.

表1 数据集统计

3.1 数据集

1)MNIST[14]

数据集由70 000个手写数字组成，大小为256像素.这些数字已经居中并进行尺寸规格化.

2)Fashion-MNIST[15]

数据集包含来自10个类别的70 000个时尚产品图片，并且图片大小与MNIST相同.

3)COIL20[16]

数据集收集从不同角度观看的20种类别的1 440个128×128灰度对象图像.

4)USPS[17]

数据集包含9 298个灰度手写数字图像，大小为16×16像素.特征为[0，2]中的浮点数.

3.2 实验设置

参数设置：根据DEC,IDEC[18],DCEC[19],VDEC[20]中网络参数的设置，自编码器网络和解码器网络的配置参数见表2，特征提取空间保持相同，都是1×10的向量.除输入层、输出层和嵌入层外，所有内部层均由ReLU非线性函数激活.编码器网络的预训练设置与IDEC完全相同.在预训练之后，将批大小设置为256个样本,初始学习率为λ=0.001,β1=0.900,β2=0.999的优化器Adam用于MNIST数据集，SGD的学习率λ=0.100，动量β=0.990用于USPS和Fashion-MNIST数据集.收敛阈值设置为δ=0.1%,并且对于MNIST，USPS和Fashion-MNIST，更新间隔分别为140次、30次和3次迭代，γ取0.1.

表2 网络配置

3.3 性能评估标准

评估指标：所有聚类方法均通过聚类精度(ACC)和归一化互信息(NMI)进行评估，这2种类型的方法广泛用于无监督学习场景中.

第1个指标是聚类精度ACC,

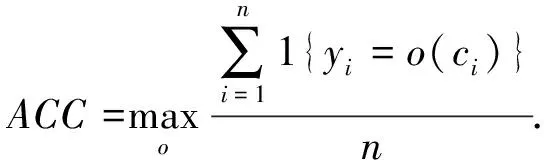
(16)

式(16)中：yi是真实标签；ci是由算法生成的聚类分布；o是一个映射函数，其作用范围是分布和标签之间所有可能的一对一映射.

第2个是归一化互信息NMI,

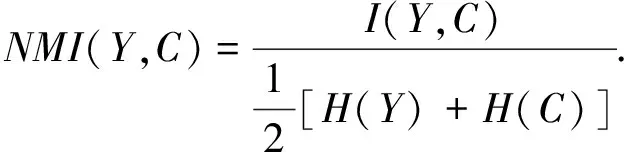
(17)

式(17)中：Y表示真实标签；C表示聚类标签；I表示互信息度量；H表示熵.

3.4 实验结果

实验分为预训练阶段和深度聚类阶段，预训练阶段损失函数变化如图3所示，深度聚类阶段准确率和损失函数如图4所示.图4中，红色曲线为聚类阶段准确率，绿色曲线为聚类损失L2，黄、蓝、青曲线为3种编码器的重构损失.通过预训练，深度聚类阶段的重构损失趋于稳定，通过降低聚类损失最终提高聚类性能.

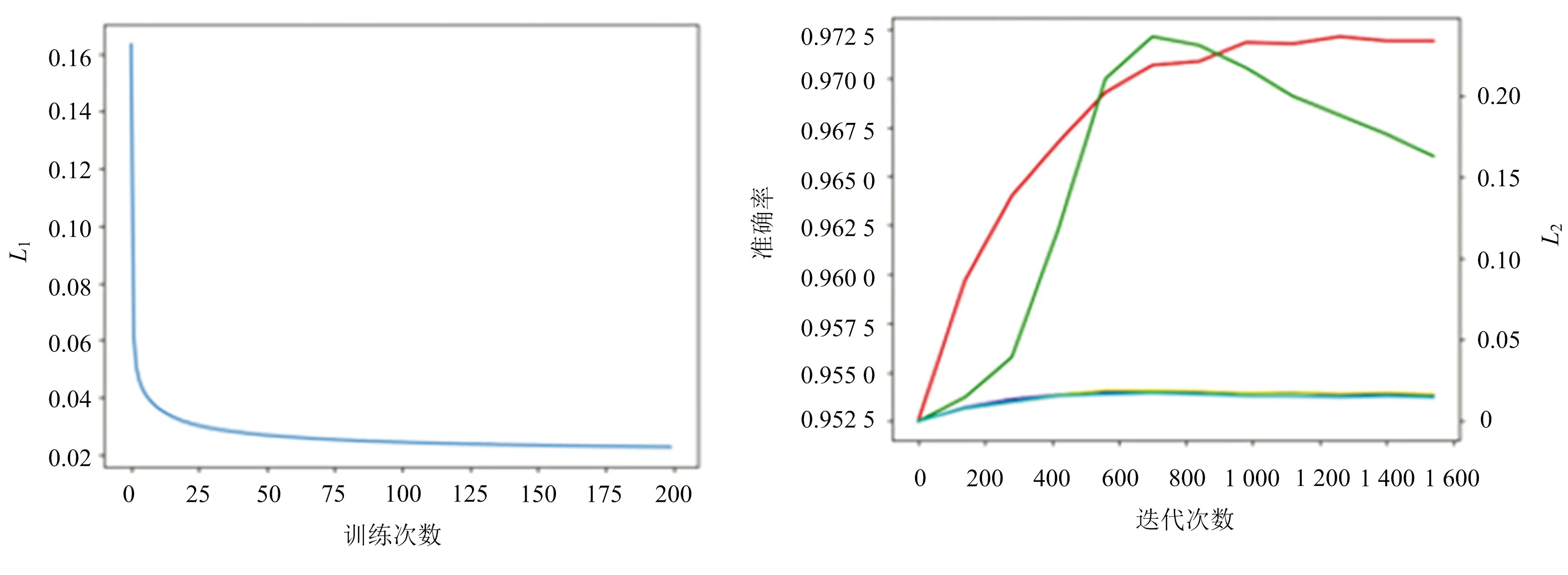
图3 预训练损失 图4 深度聚类阶段准确率、聚类损失、重构损失

通过纵向比较，即对比单独使用自编码器、卷积自编码器、变分自编码器3种深度聚类模型DEC,IDEC,DCEC,VDEC,结果见表3.本研究提出的MDEC算法的确能够很好地融合3种编码器的特征并得到更好的聚类结果.除此之外也对比了一些现在具有代表性的多模态聚类算法，如RMKMC[21],DCCA[22],DCCAE[23],DGCCA[24],DMSC[25],ASPC-DA[26],N2D[5],ClusterGAN[27],SNNL-5[6],SDCN[28],k-DAE[29]，以展示本文模型更好的性能，结果见表4.

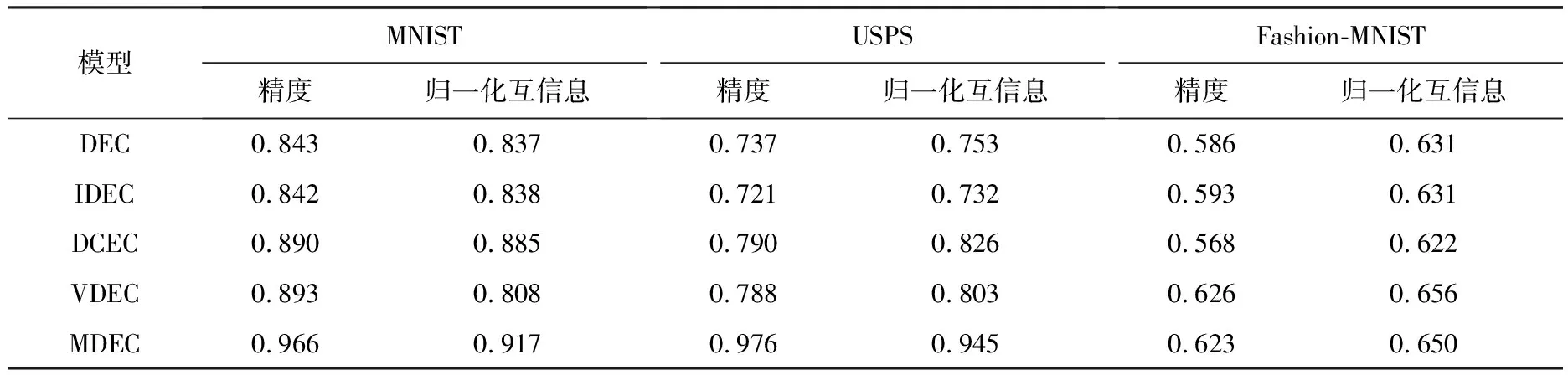
表3 算法比较(纵向)

表4 算法比较(横向)

将MDEC模型3个不同的模态通过不同的组合方式进行消融分析，结果见表5.通过测试单一模态模型、双模态模型和多模态模型，并且在MNIST数据集上进行比较分析.卷积自编码器和卷积变分自编码器都是基于卷积神经网络，对于图像的处理结果要优于一般的自编码器，但在多模态组成的模型中，自编码器模型在一定程度上能够提高整个模型的效果.此外，比较了单个编码模型与多模态融合模型的可训练参数数量、运行时间及显存占用情况,结果见表6.

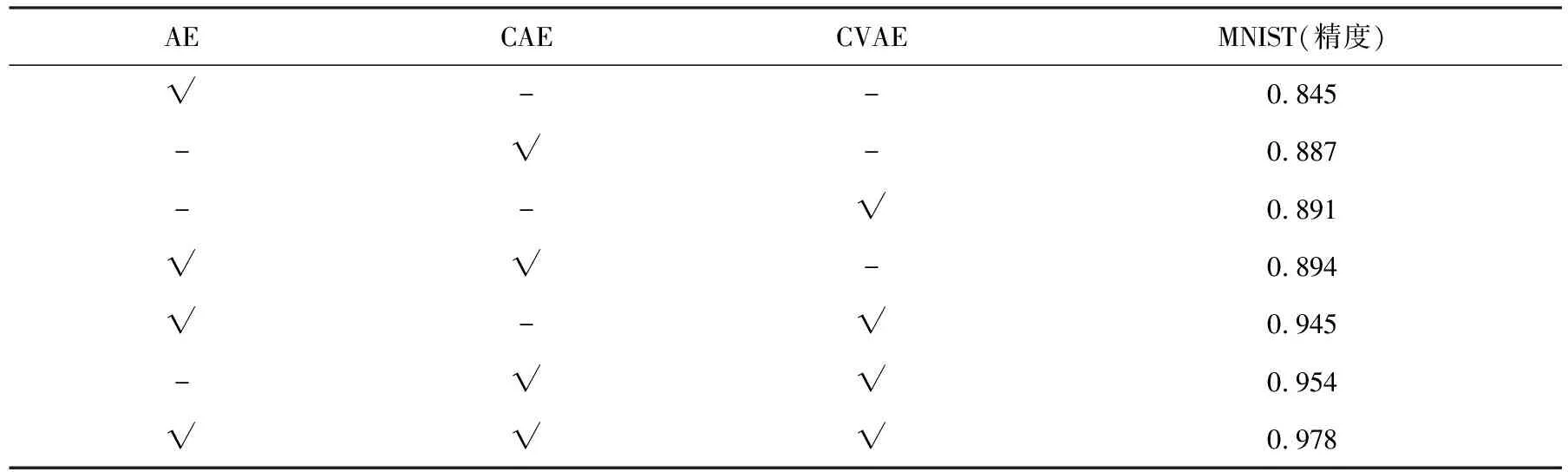
表5 多模态模型消融分析结果比较

表6 多模态与单一模型复杂度比较

4 结 语

随着海量数据的不断积累，传统算法已不能满足对海量高维数据的处理需求.聚类与深度学习的结合在这种情况下应运而生，深度神经网络能更好地学习高维数据的潜在低维特征表示，从而有利于聚类任务.本研究提出了一种新的基于自编码器的多模态深度嵌入聚类算法，并在多个数据集上验证了本模型的有效性.未来研究方向集中在以下几个方面：

1)尽管本研究提出的模型通过结合自编码器结构和嵌入式聚类模型显著提高了聚类性能，但神经网络缺乏可解释性，因此，探索深度聚类的理论保证对指导这一领域未来的研究有着无法忽视的作用.

2)本模型主要是针对图像数据集，而未对语音、文本等时序型数据进行探索，为此，未来将探索其他网络结构(例如递归神经网络)与聚类相结合的可行性.

3)本模型主要将深度神经网络与k-means相结合，而没有考虑其他的聚类任务.未来将研究多任务聚类、自学式聚类(转移聚类)等与深度神经网络相结合的算法.

4)本模型对多模态特征的融合方式局限于自适应特征融合，未来将考虑其他的融合方式，包括一些线性的和非线性的融合方式.