内三角管式快速蓄放热单元的肋片拓扑优化*

黄 河， 高佳徐， 任智彬， 赵 明

（上海理工大学 能源与动力工程学院，上海 200093）

引 言

高效蓄热技术在克服能源供需的不匹配方面发挥着重要的作用.潜热蓄热被认为是最有效的技术之一，凭借储能密度大、工作温度波动小等优势，其在工业余热回收[1]、蓄冷空调[2]和建筑节能[3]等领域中前景广阔.因此，潜热蓄热技术在过去的几十年里一直受到关注.

然而，相变材料(phase change material, PCM)的低导热率限制了储能单元的蓄、放热速率，阻碍了潜热蓄热技术的广泛应用[4].为了提高蓄热单元的传热性能，目前有两种主要的解决方案：一种方案是使用高导热材料，包括添加石墨烯[5]、纳米粒子[6]和金属泡沫[7]等高导热材料来增强导热速率.但是，这种方案通常不经济，材料的制备成本较为昂贵，且优化效果仍然有限.另一种方案是通过添加高导热肋片，改变蓄热器内部结构从而提高蓄热器性能.这种方案具有低成本、易于制造和维护的优点[8].

在蓄热器肋片结构设计方面，Ismail 等[9]通过实验和数值模拟结合的方法研究了传统圆管式蓄热器安装直肋对放热过程的影响，结果表明，增加肋片长度和厚度可以缩短放热时间.Sciacovelli 等[10]通过数值模拟，提出采用树形肋片来提高传统圆管式蓄热器装置的性能，结果表明，优化的分叉肋片结构可以提高系统效率.

连续体拓扑优化方法最初用于实现自动化智能结构设计，近几十年来在传热学领域也得到了广泛应用[11].Han 等[12]将拓扑优化方法用于仿生领域来提高散热器性能，通过实验验证了优化的蜘蛛网散热器在最小温差和压降的设计目标下有最佳的综合散热性能.Tian 等[13]将势能耗散函数作为优化目标，结果表明，优化后的肋片有仿生分形的特征，能显著提升传统圆管蓄热器的传热效率.游吟等[14]通过变密度拓扑优化方法对传统圆管式相变储热单元进行了研究，其结果揭示了自然对流对于肋片优化和系统换热能力的影响规律，并通过几何重构验证了重构模型的准确性和可靠性.

郑宇豪等[15]对比了几种异型管式蓄热器的蓄放热性能，结果表明，三角管式蓄热器有最高的蓄热效率.而目前，肋片的拓扑优化主要针对于圆管式蓄热器结构，对其他管式的拓扑研究还很少见.此外拓扑肋片结构一般较为复杂，制造难度较大.因此，本文将内三角管式蓄热器和拓扑优化相结合，并提出了一种新的肋片设计思路：从拓扑结果中提取拓扑特征以重新设计肋片.本文通过数值模拟的方法，做了如下研究：① 对比了拓扑优化肋片，以拓扑特征设计的肋片和普通垂直肋片的蓄、放热特性，验证了提取拓扑特征设计肋片方法的优越性和可行性.② 研究了蓄热过程中不同肋片模型的换热机理，对自然对流作用进行了分析.③ 运用（火 积）耗散原理对放热过程进行分析.

1 物理模型和数学模型

1.1 物理模型

如图1 所示，模型1 为文献[16]中的无肋片传统内圆管模型，内管半径Rin为 20 mm，外管半径Rout为40 mm；模型2 为设计的内三角管模型，边长ls为53.87 mm，模型2 和模型1 有相同的PCM 填充量；模型3 为模型2 的肋片拓扑优化模型；模型4 为垂直肋片（垂直于内三角管壁）模型；模型5 为发散肋片（由圆心向外发散）模型；模型6 为Y 型发散肋片模型；模型7 为2 倍金属填充量的发散肋片模型.其中，模型5 和模型6 肋片的设计过程将在本文3.2 小节给出，模型4 作为对照组.

图1 相变蓄热器物理模型简图(单位：mm)Fig. 1 Physical model diagrams of phase change accumulators (unit: mm)

1.2 拓扑优化模型

1.2.1 SIMP 密度函数插值模型

1.2.2 目标函数和约束条件

目标函数设为区域内最大或最小平均温度，基于SIMP 方法建立的拓扑优化数学模型为

1.3 相变模型

为便于研究，设立如下假设：

1) 不考虑相变过程中的过冷效应；

2) 相变过程采用低速、非稳态不可压缩的层流模型；

3) 材料均质且各向同性.

基于以上假设，控制方程形式如下：

相变过程中的物性参数如表1 所示.

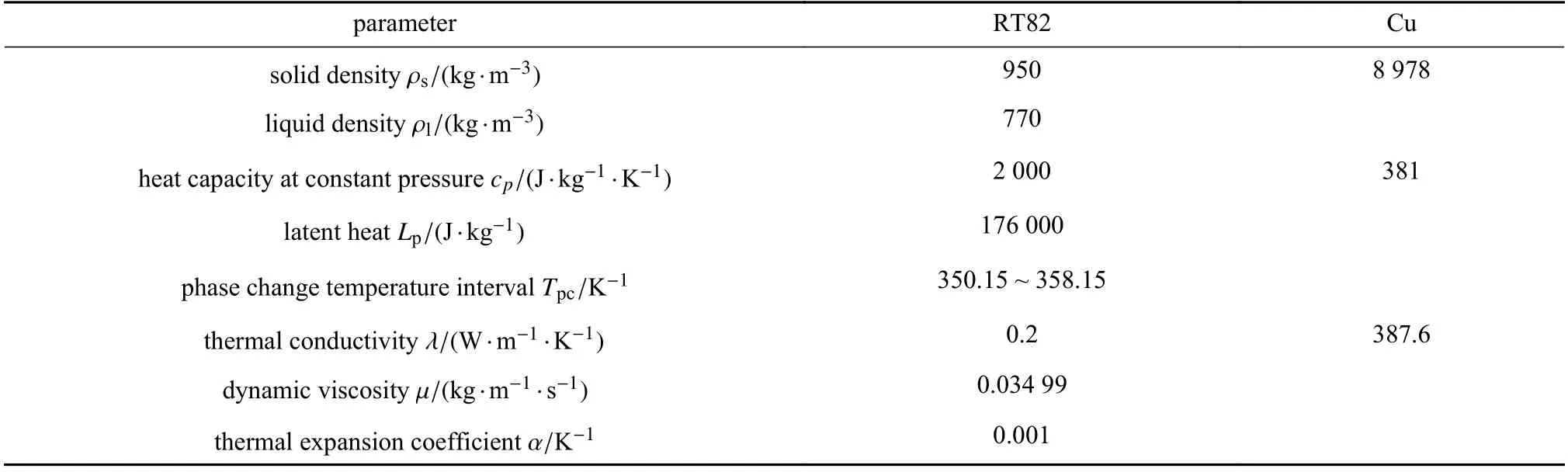
表1 物性参数表Table 1 The physical property parameter table

2 数值计算方法和模型验证

2.1 数值计算方法

优化过程采用COMSOL 软件进行稳态求解.在优化模块中设置初始参数， ρe， φ 和η 分别设为0.5，0.05 和20.根据相变过程热流密度的统计，优化区域热源设置为-18(18) W·m-2，目标函数为求解区域的最大(最小)平均温度.采用移动渐近线法（method of moving asymptotes, MMA）[19]对 ρe进行更新，优化容差为10-4，最大迭代次数为2 000.

采用ANSYS FLUENT 软件对熔化和凝固过程进行模拟.速度与压力求解方法为非稳态隐式的SIMPLEC 算法，压力项采用PRESTO 方法离散，对流项采用QUICK 格式离散，能量为2 阶迎风格式.压力、密度、速度、液相分数和能量亚松驰因子分别设为0.3，0.5，0.7，0.6 和0.9.能量方程和速度方程的收敛标准分别设为10-6和10-3，每个步长的最大迭代次数为200.

2.2 模型验证

网格无关性及时间步长验证考核结果如图2（a）、2（b）所示，综合考虑计算的可靠性和经济性，确定网格数为72 917，时间步长为0.05 s.本文的模型验证是与文献实验数据[16]进行对比完成的，由于其实验结果为无量纲化数据，因此引入Fo数：

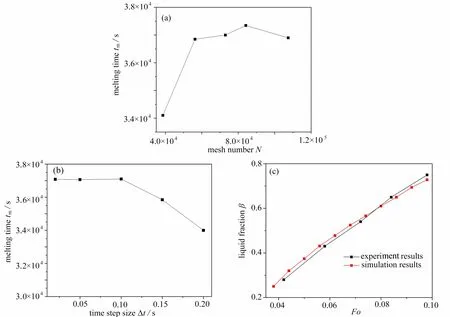
图2 模型验证：(a) 网格无关性验证；(b) 时间步长验证；(c) 模拟与实验结果对比Fig. 2 Model validations: (a) the mesh assessment; (b) the time step assessment; (c) the comparison with experiment results

3 结果与讨论

3.1 拓扑优化结果

采用COMSOL 软件，建立SIMP 拓扑优化模型，边界条件与相变过程相同.从图3 中可以看出，蓄热过程优化结果与放热优化结果具有高度一致性，这是由于优化时仅仅是边界条件和热源的不同，而优化目标和算法一致，所以差别仅仅在于铜材料的假想密度不同，因此蓄、放热过程可采用相同的模型进行分析.经过迭代计算，在蓄、放热过程中，得到其最高和最低平均温度分别为358.15 K 和308.67 K.

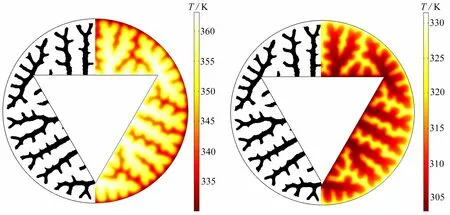
图3 蓄热（左）和放热（右）过程拓扑优化结果Fig. 3 Topology optimization results of thermal storage (left) and release (right) processes

从图3 还可以看出，每个壁面上的拓扑结构具有一致性，且在计算域内分布均匀.肋片材料从内壁面向外延伸，在其主传热路径上肋片较粗，伸展一定长度后经过分叉，虽然减小了肋片厚度，但是增大了换热面积并缩短了传热路径.肋片材料也不是单纯地垂直于壁面伸长，而是有由中心向外发散趋势的结构.综上，我们从中提取了两个拓扑特征：发散特征和分叉特征.

3.2 肋片设计

基于以上两个拓扑特征，考虑到肋片的制造与安装，我们在重构肋片的基础上继续设计了发散特征肋片模型5 和分叉特征模型肋片模型6.为便于分析与比较，分叉处取在内三角管的外接圆处，分叉后肋片厚度为0.2 mm，图4 中，从左到右分别为拓扑结果的几何重构模型3、发散肋片模型5 和分叉肋片模型6.考虑到肋片厚度对模拟结果的影响，控制模型3 肋片最大厚度为0.4 mm.各模型肋片均控制在半径为37.7 mm 的虚线圆内.各肋片模型的设计参数如表2 所示.

图4 肋片重构和特征肋片设计（单位： mm）Fig. 4 The fin reconstruction and the characteristic fin design (unit: mm)

表2 肋片设计参数表Table 2 The fin design parameter table

3.3 蓄热过程

3.3.1 蓄热过程模拟

从图5 和图6（a）中可以看出，对于无肋片模型，三角管模型的温度均匀性虽然不如传统圆管，但是其蓄热面积相比传统圆管增加了28.61%，而且三角管一角朝下的设计能大大提高熔化后期底部难熔区域的熔化速率.因此，相比于传统圆管，三角管的蓄热时间可以缩短62.5%，蓄热效率大大提升.

图5 熔化过程中的液相和温度分布Fig. 5 Liquid fractions and temperature distributions in the melting process

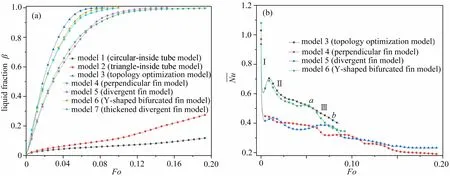
图6 液相分数和平均Nu 数在熔化过程中的变化：(a) 液相分数；(b)NuFig. 6 Changes of the liquid fraction and the average Nu number in the melting process: (a) the liquid fraction; (b)Nu

添加肋片后，蓄热效率进一步提升.为了更好地比较发散肋片的优势，我们设计了均匀分布于内管壁面且垂直壁面布置的肋片，即模型4.结果显示：模型4 管角处的温度梯度均匀性较差，并在管角肋片和垂直肋片间出现局部难熔区；发散肋片模型5 肋片间的温度梯度更为均匀，后期蓄热优势更加明显；而具有发散和分叉拓扑特征的肋片模型6 熔化效率仅次于拓扑重构模型3，分叉的肋片能将热量快速传至肋片外围，使肋片外围区域的PCM 温度和液相更加均匀.综上可知，拓扑发散肋片的特征可以使肋片间的PCM 温度和液相分布均匀，而拓扑分叉肋片的特征可以提高肋片外围PCM 的蓄热均匀性.

文献指出在一定范围内增加肋片厚度可以提高蓄热效率，为了进一步对比增加肋片厚度与分叉拓扑特征设计的不同，将模型5 的厚度增加至0.8 mm，即模型7.结果显示，加厚肋片模型7 与分叉特征模型6 的熔化速率极其接近，但这样增加了金属填充量而减少了PCM 填充量.因此，增加肋片厚度就有很大的局限性，而根据分叉拓扑特征设计的肋片不仅能提高蓄热效率，还具有省金属、低重量与高蓄热容量的优势.

3.3.2 换热的机理分析

图6（b）展示了不同肋片模型Nu随Fo数的变化情况.根据曲线所展示的特征，蓄热过程可大致分为三个阶段：阶段Ⅰ，蓄热开始时，导热作用占主导地位.因为只在壁面和肋片附近生成很薄的液态层，导热热阻小，换热剧烈，Nu数较大.随着熔化过程的进行，液态层增厚，导热热阻增大，因此Nu数急剧减小.阶段Ⅱ，自然对流对换热的影响逐渐增大.随着高温流体的增多，Nu数开始回升或保持平稳.阶段Ⅲ，自然对流作用开始衰减.热流体逐渐增多且温度趋于一致，产生自然对流的动力减弱，Nu数持续下降.

从图6（b）中还可以明显看出，肋片拓扑模型3 和Y 型分叉模型6 的Nu大致相近，且高于同一时刻的其他模型，说明其自然对流作用较强；垂直肋片模型4 只在蓄热前期Nu略高于模型5，而中后期要低于模型5，这是因为垂直布置的肋片间距较小，间距减小在一定程度上加快了肋片间PCM 的熔化速率，从而加速了流动提升对流换热效果，但是这样严重滞后了管角处材料的熔化.

为了进一步探究分叉特征对换热效果的影响，我们对模型5 和6 三角管外接圆内外流体区域（I 区域和O 区域）的平均流速进行了统计与对比，如图7 所示.从图8 中可以看出，模型5 和6 平均流速的衰减点（a，b）与其各自的自然对流作用衰减点（图6（b）中的点a，b）基本一致，这验证了Nu揭示换热机理的可靠性和准确性.对于I 区域，当Fo＜0.05 时，两个模型的平均流速基本一致，其后模型6 平均流速的最大值小于模型5，而当蓄热接近尾声时，两个模型的流速均逐渐减小.这是因为肋片结构在I 区域是相同的，所以蓄热过程只有进行到一定程度时，外围温度场和流场发生明显变化，O 区域结构的差异才会对I 区域的流动产生影响；而当蓄热基本结束时，流场温度差减小，密度趋于一致，产生自然对流的动力减弱，因而流速均逐渐减小.而对于O 区域，分叉结构使得模型6 中O 区域内的PCM 比模型5 熔化得更快，且形成了更多更小的自然对流区域，所以同一时刻模型6 在O 区域的液相率更大，Fo＜0.05 时，同时刻的流速也更大.进入熔化后期时，分叉肋片模型的最大流速小于直肋模型，且考虑液相相近时（如点a和点b处），模型6 的流速也要小于模型5.因此，虽然分叉结构阻碍了流体在大空间上的流动，减小了整体的流速，但是其形成了更多小的自然对流区域，使流动带来的换热更为有效，从而提高了蓄热器的蓄热能力.

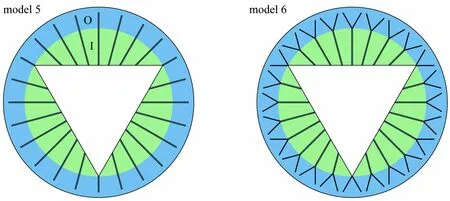
图7 平均速度区域监测示意图Fig. 7 Schematic diagram of the regional monitoring of average velocities

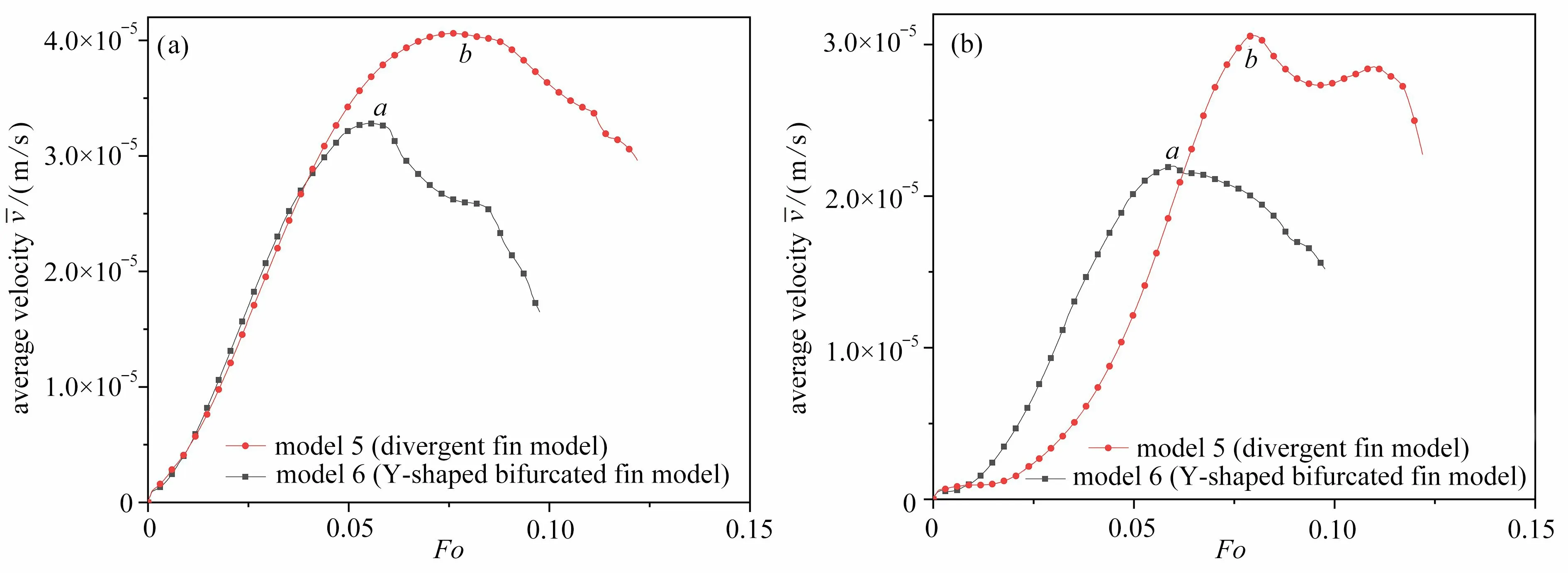
图8 区域平均速度变化对比： (a) 区域I 的平均速度；(b) 区域O 的平均速度Fig. 8 Comparison of regional average velocity changes: (a) the average velocity in zone I; (b) the average velocity in zone O

3.4 放热过程

3.4.1 放热过程模拟

根据模拟结果，在放热过程中，对于无肋片模型，三角管模型凭借着换热面积优势，相比传统圆管减少了16.72%的凝固时间.

如图9 和图10 所示，添加肋片后，凝固速率大大提升.与蓄热过程相似，模型4 管角处温度分布依旧极不均匀，出现难凝固的现象，因此总体凝固时间大大延长；经过拓扑特征优化后，温度场均匀性明显提升，其中分叉拓扑特征模型6 相比于接近2 倍金属填充量的加厚肋片模型7，减少了20.48%的放热时间.因此，拓扑特征设计的优化方案同样适用于放热过程.

3.4.2 放热过程的(火 积)耗散分析

从图10（b）中可以看出，Nu随放热过程的进行逐渐减小.这是因为随着液相PCM 的凝固，液态区域出现衰减，流体流动受到阻滞，这使得自然对流对换热的影响逐渐减小.从图9 还可以看出，添加肋片后，蓄热器上下部分的液相和温度分布较为对称，说明导热作用占据着主导地位.因此，为了更好地分析拓扑特征结构对导热热阻的影响，引入（火 积）耗散[21-22]理论，其中（火 积）耗散的定义如下：

图9 凝固过程中的液相和温度分布Fig. 9 Liquid fractions and temperature distributions in the solidification process

图10 液相分数和平均Nu 数在凝固过程中的变化：(a) 液相分数β；(b)NuFig. 10 Changes of the liquid fraction and the average Nu number in the solidification process: (a) the liquid fraction β; (b)Nu

式中T′为 热源传热温度，T为系统内部温度， δQ为传输的热量.

从式（11）中可以看出，温差传热的过程中必然伴随着（火 积）耗散.对于散热问题，边界条件为绝热或定温时，（火 积）耗散最小，散热体的平均温度最小，传热效果最好.

由图11 可知，模型3 的（火 积）耗散最小，相当于拓扑重构模型热阻最小，放热过程中的温度梯度最为均匀，放热可逆性最好，传递热量的能力最强，其次是Y型拓扑特征肋片模型.此外，垂直肋片模型后期（火 积）耗散率增大，这是因为难熔区的出现，使其局部温度梯度增大，温度梯度均匀性较差，总体热阻较大，放热能力较差.

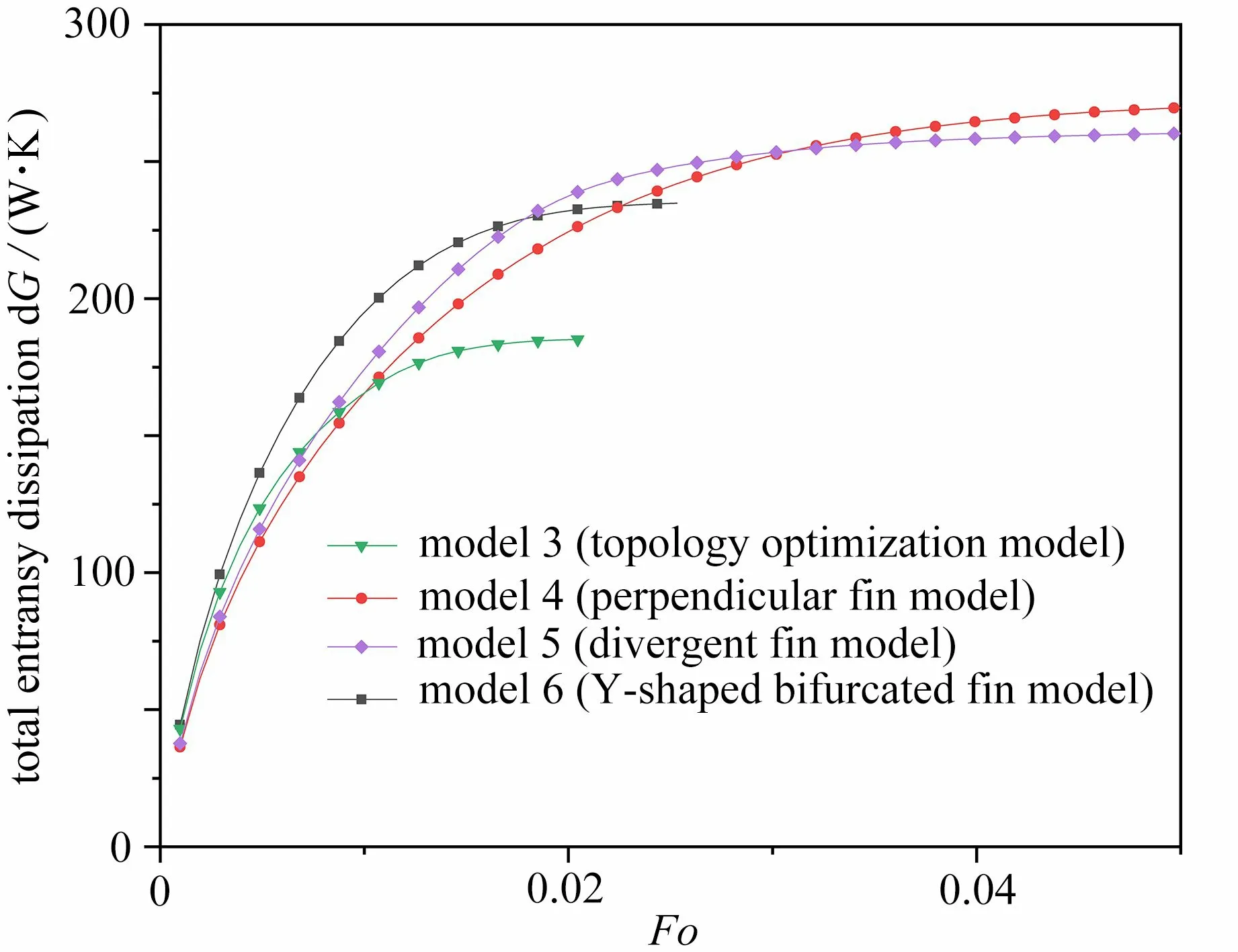
图11 凝固过程中的总(火 积)耗散Fig. 11 Total entransy dissipations in the solidification process

事实上，通过（火 积）耗散原理揭示的导热能力，也能体现拓扑重构及其特征模型的蓄热优势，这也证明了拓扑优化方法的可行性和有效性.

4 总 结

本文通过研究得出了如下结论：

1) 对于无肋片的情况，内三角管式蓄热器相比传统圆管蓄热器更有优势，蓄热时间缩短了62.5%，放热时间缩短了16.72%.

2) 拓扑优化方法在三角管中也有很好的应用.通过提取拓扑特征，一方面简化了拓扑肋片的加工工艺，另一方面提升了蓄热器的蓄放热效率，且具有省金属、低重量与高蓄热容量的优势.

3) 根据蓄热过程的Nu数 随Fo的变化情况，蓄热器蓄热过程可以大致分为3 个阶段，而且根据分叉拓扑特征能形成更多小的自然对流区域，虽然降低了流速，但是使流动带来的换热更为有效；放热过程中，拓扑及其特征设计的肋片模型（火积 ）耗散更小，温度梯度更加均匀，可逆性更好.

参考文献（ References ） ：

［1］JOUHARA H, KHORDEHGAH N, ALMAHMOUD S, et al. Waste heat recovery technologies and applications[J].Thermal Science and Engineering Progress, 2018, 6: 268-289.

［2］BISTA S, HOSSEINI S E, OWENS E, et al. Performance improvement and energy consumption reduction in refrigeration systems using phase change material (PCM)[J].Applied Thermal Engineering, 2018, 142: 723-735.

［3］JIN X, SHI D, MEDINA M A, et al. Optimal location of PCM layer in building walls under Nanjing (China)weather conditions[J].Journal of Thermal Analysis and Calorimetry, 2017, 129（3）: 1767-1778.

［4］AGYENIM F, HEWITT N, EAMES P, et al. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS)[J].Renewable & Sustainable Energy Reviews,2010, 14（2）: 615-628.

［5］ZOU D, MA X, LIU X, et al. Thermal performance enhancement of composite phase change materials (PCM) using graphene and carbon nanotubes as additives for the potential application in lithium-ion power battery[J].International Journal of Heat and Mass Transfer, 2018, 120: 33-41.

［6］SHEIKHOLESLAMI M, HAQ R, SHAFEE A, et al. Heat transfer simulation of heat storage unit with nanoparticles and fins through a heat exchanger[J].International Journal of Heat and Mass Transfer, 2019, 135: 470-478.

［7］ZHENG H, WANG C, LIU Q, et al. Thermal performance of copper foam/paraffin composite phase change material[J].Energy Conversion and Management, 2018, 157: 372-381.

［8］PIZZOLATO A, SHARMA A, MAUTE K, et al. Design of effective fins for fast PCM melting and solidification in shell-and-tube latent heat thermal energy storage through topology optimization[J].Applied Energy, 2017,208: 210-227.

［9］ISMAIL K A R, ALVES C L F, MODESTO M S. Numerical and experimental study on the solidification of PCM around a vertical axially finned isothermal cylinder[J].Applied Thermal Engineering, 2001, 21（1）: 53-77.

［10］SCIACOVELLI A, GAGLIARDI F, VERDA V. Maximization of performance of a PCM latent heat storage system with innovative fins[J].Applied Energy, 2015, 137: 707-715.

［11］ 夏天翔, 姚卫星. 连续体结构拓扑优化方法评述[J]. 航空工程进展, 2011, 2（1）: 1-11. （XIA Tianxiang, YAO Weixing. A survey of topology optimization of continuum structure[J].Advances in Aeronautical Science and Engineering, 2011, 2（1）: 1-11.（in Chinese））

［12］HAN X, LIU H, XIE G, et al. Topology optimization for spider web heat sinks for electronic cooling[J].Applied Thermal Engineering, 2021, 195: 117154.

［13］TIAN Y, LIU X, XU Q, et al. Bionic topology optimization of fins for rapid latent heat thermal energy storage[J].Applied Thermal Engineering, 2021, 194: 117104.

［14］ 游吟, 赵耀, 赵长颖, 等. 相变储热单元内肋片结构的拓扑优化[J]. 科学通报, 2019, 64（11）: 1191-1199. （YOU Yin,ZHAO Yao, ZHAO Changying, et al. The topology optimization of the fin structure in latent heat storage[J].Chinese Science Bulletin, 2019, 64（11）: 1191-1199.（in Chinese））

［15］ 郑宇豪, 赵明. 整体旋转式三角形管相变蓄热器性能及场协同分析[J]. 建模与仿真, 2021, 10（2）: 292-304. （ZHENG Yuhao, ZHAO Ming. Performance and field synergy analysis of integral rotating phase change heat accumulator with triangular tube[J].Modeling and Simulation, 2021, 10（2）: 292-304.（in Chinese））

［16］YUAN Y, CAO X, XIANG B, et al. Effect of installation angle of fins on melting characteristics of annular unit for latent heat thermal energy storage[J].Solar Energy, 2016, 136: 365-378.

［17］TCHERNIAK D. Topology optimization of resonating structures using SIMP method[J].International Journal for Numerical Methods in Engineering, 2002, 54（11）: 1605-1622.

［18］ 孙国民, 张效忠, 孙延华. 基于特征值分析的多尺度结构优化设计方法[J]. 应用数学和力学, 2019, 40（6）: 630-640.（SUN Guomin, ZHANG Xiaozhong, SUN Yanhua. Multi-scale structure optimization design based on eigenvalue analysis[J].Applied Mathematics and Mechanics, 2019, 40（6）: 630-640.（in Chinese））

［19］SVANBERG K. The method of moving asymptotes: a new method for structural optimization[J].International Journal for Numerical Methods in Engineering, 1987, 24（2）: 359-373.

［20］KAMKARI B, SHOKOUHMAND H. Experimental investigation of phase change material melting in rectangular enclosures with horizontal partial fins[J].International Journal of Heat and Mass Transfer, 2014, 78: 839-851.

［21］GUO Z Y, ZHU H Y, LIANG X G. Entransy: a physical quantity describing heat transfer ability[J].International Journal of Heat and Mass Transfer, 2007, 50（13/14）: 2545-2556.

［22］ 韩光泽, 过增元. 导热能力损耗的机理及其数学表述[J]. 中国电机工程学报, 2007, 27（17）: 98-102. （HAN Guangze,GUO Zengyuan. Physical mechanism of heat conduction ability dissipation and its analytical expression[J].Proceedings of the Chinese Society of Electrical Engineering, 2007, 27（17）: 98-102.（in Chinese））