边界骨柱对石膏面板轻木剪力墙抗剪性能的影响研究∗

柏 洁 周 华 丁俊豪 任廷亮

（1.贵州大学土木工程学院，贵州 贵阳 550025；2.贵州电力建设监理咨询有限责任公司，贵州 贵阳550025；3.贵阳人文科技学院，贵州 贵阳 550025）

轻型木结构剪力墙通常由规格材、木基结构板或石膏板制作而成，承受由地震作用和风荷载产生的全部剪力。根据GB 50005—2017《木结构设计标准》相关规定，在剪力墙受剪设计时，木基结构板材剪力墙的抗剪强度设计值和抗剪刚度均应根据面板厚度、钉直径、钉入深度及面板边缘钉间距查表确定，不考虑木骨架对剪力墙抗剪性能的影响，对于剪力墙两侧边界骨柱，按剪力墙平面内弯矩产生的轴向力进行承载力验算。

国内外对轻型木结构剪力墙抗剪性能的研究主要集中在墙体材料、构造方式、边界条件等影响因素。墙体覆面材料的研究主要涉及OSB板、石膏板[1-2]、秸秆板[3-5]、竹面板[6-7]等。有关不同构造对轻木结构剪力墙受力性能的影响研究，主要集中在长高比、钉直径、钉间距、骨柱间距等方面[8-14]。边界条件的研究主要针对竖向荷载[15-16]和上部刚度[17]等。此外，还有对加强措施[18-20]、不同框架混合结构[21-23]、台风荷载响应[24]、数值模拟方法[25-27]的研究等。现有研究尚未涉及边界骨柱对轻型木结构剪力墙抗剪性能的影响。

本课题组的前期试验表明，石膏面板轻木剪力墙的抗剪破坏主要由石膏面板钉连接破坏导致，墙骨柱特别是边界骨柱出现明显的上拔变形。为进一步研究轻木剪力墙边界骨柱对剪力墙抗剪性能的影响，本文在改变边界骨柱数量后进行单调加载试验，对边界骨柱对剪力墙的抗剪强度、抗剪刚度及延性等的影响进行对比研究，推导了边界骨柱对剪力墙抗剪性能的贡献作用，并提出计算公式，为剪力墙的抗剪强度设计值和抗剪刚度提供更为精细的取值依据。

1 剪力墙抗剪性能试验

1.1 墙体设计与制作

依据GB 50005—2017 标准的构造要求，制作4 个轻型木结构剪力墙试件。骨柱、顶梁板和底梁板均采用加拿大Ιc级SPF（云杉-松木-冷杉）规格材，截面尺寸为38 mm × 89 mm；墙面板采用12 mm厚纸面石膏板（贵州泰福石膏有限公司）；骨柱由2 根国产钢钉分别与顶梁板和底梁板连接，钉帽直径8.5 mm，钉长90 mm；面板钉为国产木螺钉，钉帽直径4.2 mm，钉长50 mm，沿板边缘钉间距150 mm，板中钉间距300 mm；墙平面尺寸分别为2 400 mm × 2 400 mm和1 200 mm ×2400 mm；墙体底部两端各设置一个抗拔紧固件，通过2 个直径为16 mm的螺栓与边墙骨柱连接，1 个直径为16 mm的螺栓与底梁板相连。

通过对比无面板试件（LW-1）和单面覆板试件（LW-2），考察剪力墙抗剪能力中骨架与面板的分配比例。通过对比边界单骨柱（LW-3）和边界双骨柱试件（LW-4），考察边界骨柱对剪力墙抗剪性能的贡献作用并进行量化。试件编号如表1所示，试件构造如图1所示。

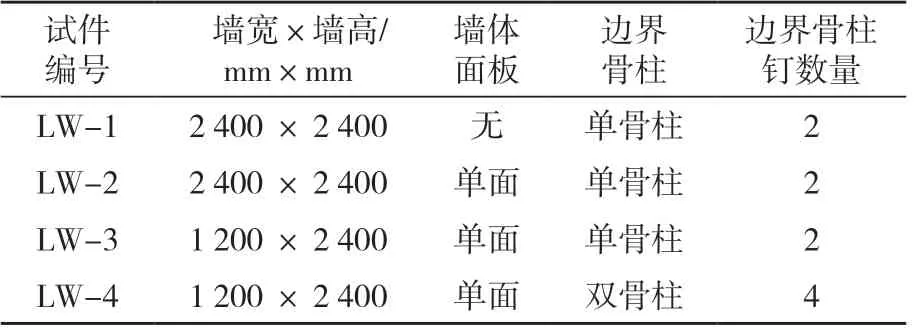
表1 试件设计Tab.1 Design of specimen

图1 试件示意图Fig. 1 Specimen diagram

1.2 材料的基本性能

SPF规格材的平均基本密度为0.47 g/cm3，弹性模量为6 500 N/mm2；纸面石膏板的面密度为9.5 kg/m2，弹性模量为1 680 N/mm2；骨柱钉光圆杆处实测平均直径为3.62 mm，平均长度为89.74 mm，平均弯曲屈服强度为691.07 MPa；面板钉光圆杆处实测平均直径为3.01 mm，平均长度为49.37 mm，平均弯曲屈服强度为917.07 MPa。

1.3 加载装置与测量

采用贵州大学土木工程学院结构工程实验室MTS液压伺服加载系统进行加载试验。试验墙体底侧通过螺栓固定于专用方钢管地梁上，墙体上侧通过4 根拉杆固定于 MTS 作动器端头。采用 4 个拉杆式 YHD 型位移传感器，分别测量顶梁板、地梁板水平位移和边界骨柱竖向位移。试验装置和测点布置如图2 所示。根据GB/T 37745—2019《木结构剪力墙静载和低周反复水平加载试验方法》，单调加载采用位移控制，加载速率为2 mm/min，数据采集频率为 2 Hz。当试验荷载下降至极限载荷的85%或出现严重破坏时停止加载。

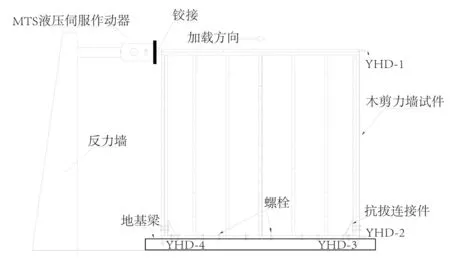
图2 试验加载装置和测点布置Fig.2 Test setup and measuring location arrangement

2 结果与分析

2.1 破坏形态

2.1.1 带面板剪力墙

带面板剪力墙极限荷载时的变形如图3所示。在水平荷载前期，剪力墙基本处于弹性状态，仅在边界骨柱及次边界骨柱出现少量钉节点拔出，无明显的面板钉破坏和墙骨架变形。当位移荷载逐渐增大，面板边缘钉节点出现了不同方向的钉孔滑移，木骨架呈弯曲型侧向变形，且骨柱从边缘至中心逐渐出现钉节点拔出现象（图5）。当达到极限荷载时，四角一定范围的边缘钉节点钉孔范围面板破坏（图6），与钉脱离，面板出现明显的平面内转动，与墙骨架不再协调变形，墙骨架侧向变形继续增加，荷载逐渐下降，最终剪力墙破坏。

图3 带面板剪力墙变形形态Fig.3 Deformation of shear wall with panels

图4 剪力墙骨架变形形态Fig.4 Deformation of shear wall without panels

图5 骨柱上拔Fig.5 Pull-out of studs

图6 面板钉破坏Fig.6 Failure of panel-stud nailed joints

2.1.2 剪力墙骨架

剪力墙骨架极限荷载时变形情况如图4 所示。无面板的剪力墙骨架试件（LW-1）在水平位移荷载作用下首先出现平行四边形变形，随后骨柱出现钉节点拔出现象，且骨柱上拔量随着各骨柱距剪力墙中心距离增加而加大，边界骨柱的上拔量远大于其他骨柱。由于没有抗拔紧固件的约束，墙骨架的侧向位移远大于带面板剪力墙，且墙骨柱无明显的弯曲变形，最终破坏由骨柱钉节点拔出所致。

2.2 荷载位移曲线

图7 所示为有无面板剪力墙的荷载位移曲线。由图明显可见，无面板的剪力墙骨架抗剪承载力仅为有面板剪力墙抗剪承载力的12%左右，而变形量远大于有面板剪力墙，说明轻型木结构剪力墙的抗剪承载力主要由面板提供，墙骨架对其影响较小。图8 为不同边界构件剪力墙荷载位移曲线的对比，设置边界双骨柱的试件（LW-4）较边界单骨柱试件（LW-3）的极限荷载略大，两个试件在受力前期抗剪性能差异不大，但在70%极限荷载后，LW-3 的曲线出现转折，位移较LW-4 增大，达到极限荷载后，LW-3 荷载下降更明显。

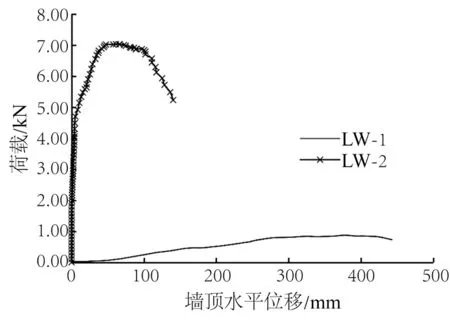
图7 荷载-位移曲线对比Fig.7 Comparison of load-displacement curves

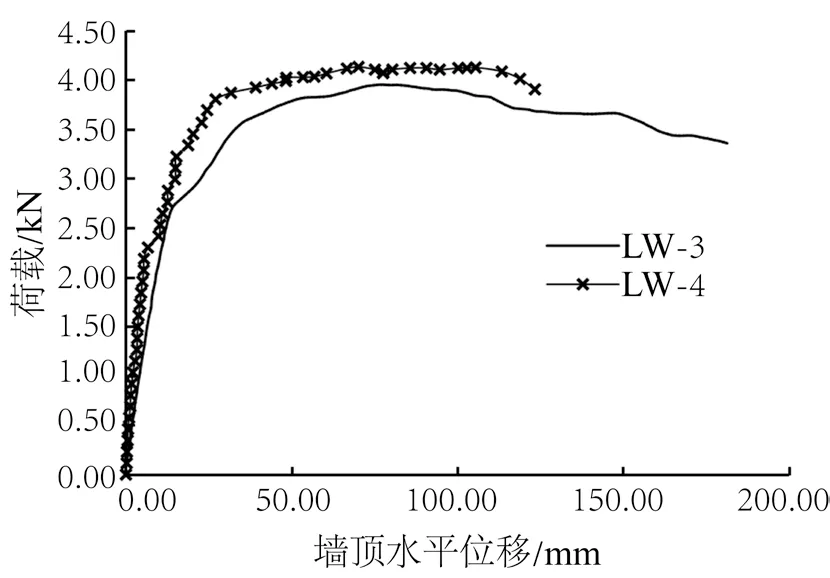
图8 荷载-位移曲线对比Fig.8 Comparison of load-displacement curves

2.3 主要试验结果

在单调加载试验中，定义当荷载下降至85%极限荷载时为破坏荷载，相应位移为破坏位移，根据GB/T 37745—2019 标准定义弹性抗剪刚度为：

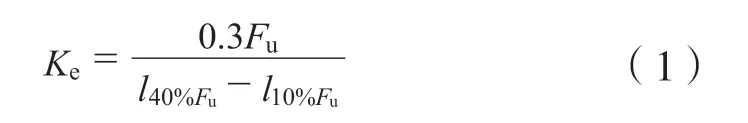
极限荷载对应抗剪刚度为：

式中：Ke为弹性抗剪刚度，N/mm；Ku为极限荷载对应抗剪刚度，N/mm；Fu为极限荷载，N；δu为极限位移，mm；l10%Fu、l40%Fu分别为10%Fu和40%Fu相应的位移，mm。

如表2 所示，无面板的剪力墙骨架承载能力约为有面板剪力墙的12%，在荷载前期骨架抗剪刚度几乎可以忽略。达到极限荷载后，由于面板开始破坏，骨架对剪力墙抗侧性能的影响开始体现。设置边界双骨柱较边界单骨柱可提高极限荷载和抗剪强度约4.6%，提高极限荷载对应抗剪刚度约12.2%，边界双骨柱对剪力墙受力性能的影响在面板钉节点出现破坏后的受力后期最为明显。

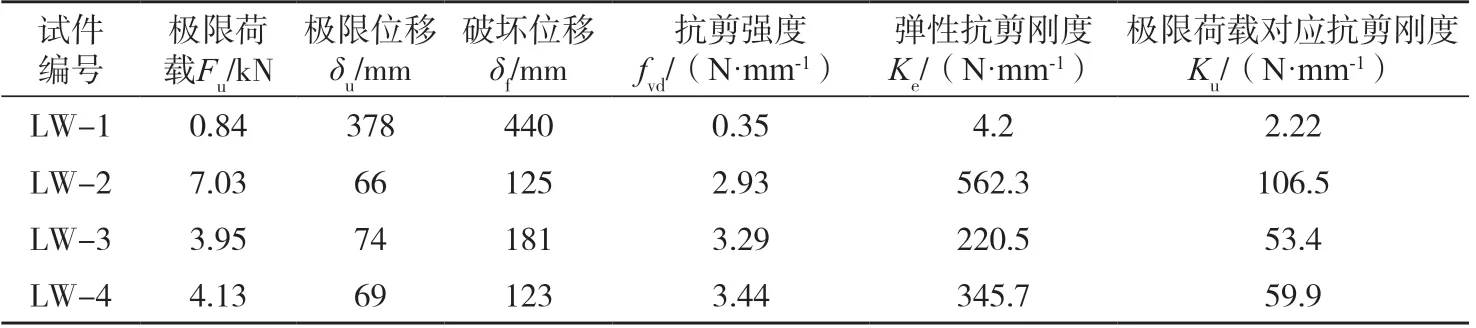
表2 主要试验结果Tab.2 Main test results

3 有限元分析

采用 ABAQUS 有限元软件对石膏面板轻木剪力墙进行非线性参数分析，共建立6个剪力墙模型，分别为墙长为1 200 mm的边界单骨柱（W12D）和边界双骨柱（W12S）模型，墙长为2 400 mm的边界单骨柱（W24D）和边界双骨柱（W24S）模型，墙长为3 600 mm的边界单骨柱（W36D）和边界双骨柱（W36S）模型，所有模型墙高为2 400 mm，单面覆12 mm厚石膏面板，在顶梁板施加水平荷载。采用梁单元B21定义剪力墙骨架，壳单元CPS4R定义石膏面板，钉连接节点采用两个方向非线性弹簧单元Spring2进行模拟，木材和石膏面板材料性能按试验值，骨架钉和面板钉力学性能均按课题组实测确定，如图9所示。

图9 骨架钉节点抗剪（a）、抗拔（b）和面板钉抗剪（c）拟合曲线图Fig.9 Shear (a), pullout (b) curves of skeleton nail joints and shear (c) curves of panel-stud nailed joints

3.1 分析结果

以模型W12D和W12S为例，模拟荷载位移曲线与试验曲线对比如图10 所示。由图可知，有限元模拟结果与试验结果吻合较好。图11 为极限荷载下墙体位移云图，与试验位移相似，在加载一侧边界骨柱有明显的上拔，墙体整体呈倾覆状变形，墙面板发生明显的平面内转动。图12 为墙面板平面内剪应力云图，随着荷载增加，剪应力较大区域从加载点一侧逐渐向墙体中心转移，下部剪应力总体较上部大。

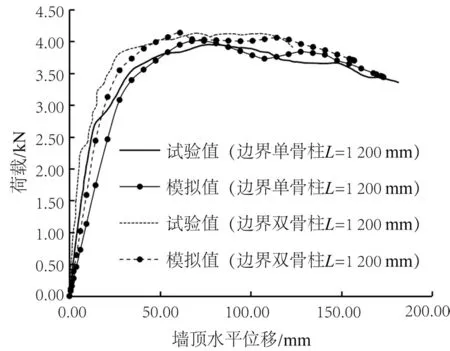
图10 荷载位移曲线对比Fig.10 Comparison of load-displacement curves

图11 位移云图Fig.11 Cloud diagram of displacement

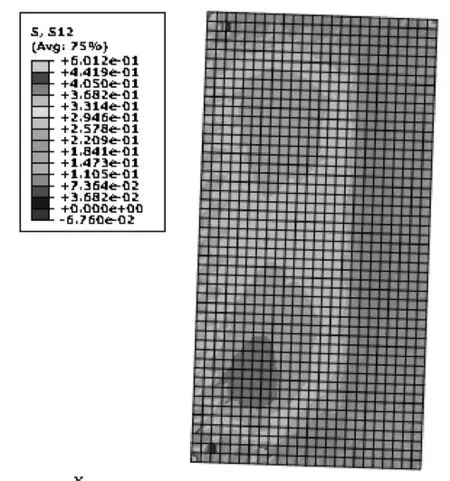
图12 剪应力云图Fig.12 Cloud diagram of shear stress

3.2 剪力分配比例

在有限元模拟结果中，沿剪力墙底部同一路径提取极限荷载时墙面板及骨柱水平方向的剪应力，分别计算墙面板与骨柱承担的剪力及相应的剪力分配比例，见表3。由表可知，随着墙长增加，极限荷载相应提高，呈明显的正相关性，采用边界双骨柱的墙体极限承载力较边界单骨柱时略有提高，但提升效果不明显。当边界骨柱采用单骨柱时，骨架剪力分配比例约0.05；当边界骨柱采用双骨柱时，骨架剪力分配比例明显提高，达到0.15 左右。

4 边界骨柱对剪力墙抗剪性能的影响

根据试验和有限元分析结果可知，边界双骨柱对剪力墙承载力影响不大，因此仅考虑骨架承担部分剪力后的变形对剪力墙变形能力和抗剪刚度产生的影响。

4.1 剪力墙顶部的水平位移构成

轻型木结构剪力墙顶部的水平位移由面板变形、骨架变形和层转角变形三部分组成，其中，面板变形δW包含面板剪切及面板钉滑移变形；骨架变形包含骨架在水平剪力作用下的变形δV、骨架钉或抗拔紧固件的变形δd。本文不考虑层转角变形，剪力墙顶部的水平位移如公式（3）所示，面板变形量按公式（4）计算。

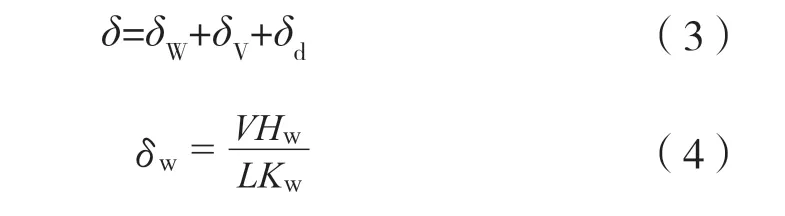
式中：δ为剪力墙顶部水平位移，mm；δW为面板变形，mm；δV为骨架变形，mm；δd为骨架钉或抗拔紧固件变形，mm；V为剪力墙顶部剪力设计值，N；Hw为剪力墙高度，mm；L为剪力墙长度，mm；Kw为剪力墙剪切刚度，N/mm，由规范或试验得出。

4.2 骨架变形δV

骨架在与面板共同作用时，可按剪力墙全截面受弯计算骨架变形，边界骨柱为单骨柱时骨架变形为：

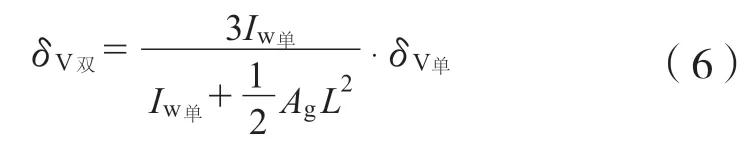
由上式可知，采用边界双骨柱时，由于骨架承担剪力比例增加，相应的骨架变形大于边界单骨柱时，且当墙长越小时，边界设置双骨柱时骨架变形δV较单骨柱时增加越明显。

4.3 骨架钉变形δd

骨架钉在水平剪力作用下，变形由钉剪切变形δgV和钉拔出变形δgb组成。由于骨架承担水平剪力远小于课题组前期骨架钉抗剪试验的承载力，因此钉剪切变形δgV可以忽略。骨架钉拔出变形由边界骨柱承受的轴向拉力N导致，按公式（7）计算：

式中：N为边界骨柱的拉力设计值，N；B0为剪力墙两侧边界骨柱的中心距，mm，独立墙肢时B0=L。

当采用边界双骨柱时，由于边骨架钉数量为单骨柱时的2 倍，因此，钉拔出变形δgb双=0.5δgb单，根据课题组完成的骨架钉抗拔试验极限位移，δgb单=8.5mm。

4.4 抗剪刚度提高比例

根据上述公式，设置边界双骨柱时的剪力墙顶部水平位移δ双较设置边界单骨柱时的剪力墙顶部水平位移δ单的减少值为：

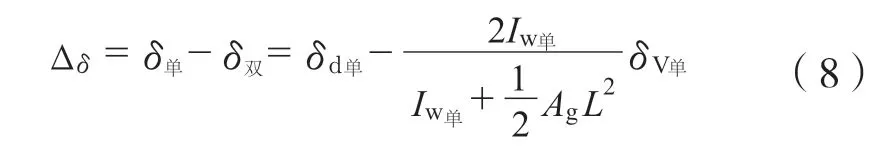
式中:Δδ为设置边界单骨柱与边界双骨柱时剪力墙顶部水平位移差，mm。

设置边界双骨柱时的剪力墙抗剪刚度提高系数β为：

式中：K单、K双分别为设置边界单骨柱和边界双骨柱时的剪力墙抗剪刚度，N/mm。

以 试 件LW-3 和LW-4 为 例，试 件LW-3：Iw单=2 705 600 000 mm4，Ag=3 382 mm2，L=1 200 mm，δ单=74 mm，K单=53.4 N/mm，则计算试件LW-4：β=1.128，K双=60.24 N/mm，计算剪力墙抗剪刚度与试验抗剪刚度相差0.6%，公式计算吻合度较高。

5 结论

本文对边界骨柱对石膏面板轻木剪力墙抗剪性能的影响进行研究，得出以下结论：

1）边界骨柱对石膏面板轻木结构剪力墙墙体抗剪承载力影响不大，设置边界双骨柱可提高极限荷载对应的抗剪刚度。

2）采用边界双骨柱可提高骨架剪力分配比例，从而延缓面板钉连接破坏，提升剪力墙抗剪性能。当采用边界单骨柱时，骨架剪力分配比例约为0.05；采用边界双骨柱时，骨架剪力分配比例约为0.15。随着墙长增加，骨架剪力墙分配比例略有提升。

3）本文提出的设置边界双骨柱抗剪刚度提高系数公式与边界骨柱截面面积、墙长等有关，经与试验结果对比，公式拟合度较好。