超宽带技术下基于软两步法的目标定位
谢 莹
(江苏联合职业技术学院 苏州工业园区分院,江苏 苏州 215123)
0 引言
近年来,超宽带(UWB,ultra-wide band)技术由于其精确的定位能力而引起了人们的广泛关注[1-3]。特别是在密集的多路径室内无线环境中,使得位置估计成为一项非常具有挑战性的任务。
采用具有几GHz带宽的UWB极短时域脉冲,可以提供高时间分辨率,从而解决多径分量并穿透障碍物的问题;UWB系统利用持续时间小于1 ns的非常短的脉冲,超宽带波形持续时间短使得系统能够提供高数据速率通信以及精确定位。无线局域网终端等传统室内定位技术的精度为几m,而超宽带定位的精度为cm级;然而,由于传输功率的限制,超宽带定位系统一般只适用于室内目标的定位。现有的窄带无线电系统(电视广播、无线局域网、卫星、全球定位系统等)使用的频段与分配给超宽带的频段重叠。因此,为了保护现有的窄带无线电系统,UWB无线电系统的传输功率被严格控制在-41.3 dBm/MHz以下。因此,超宽带传输距离有限,适合在室内定位系统中应用;从实际的角度来看,UWB已经成为具有IEEE802.15.4a定位能力的射频标签应用的候选方案。IEEE 802.15.4a是一个致力于为位置感知网络提供低数据速率通信的新物理层的标准化组织;一方面,超宽带定位的问题之一是UWB系统需要精度达到数十ps的同步电路。如此精确地设计和控制模拟电路的特性是非常困难的。另一方面,如果在数字域处理超宽带信号,需要非常高的采样率和高分辨率的模拟数字转换器(ADC,analog to digital converter),而ADC的成本和功耗可能会非常高。文献[4]提出了一种用于高数据速率、低功耗、近距离通信的数字化多脉冲位置调制脉冲无线电UWB收发器。通过利用两个脉冲之间的时间差调制数据,克服了数据速率对系统时钟频率的依赖,还实现了基于完全数字电路的调制和解调。在相同的时钟频率下,与传统的UWB调制方案相比,该技术的数据速率提高了5倍。此外,该技术使设计一个无时钟接收器成为可能;文献[5]提出了用高速比较器对进行UWB测距的方法,提出了一种具有高速比较器的超宽带定位系统,设计了一种UWB通信收发器系统架构。该收发器采用脉冲无线电UWB通信,频率为10 GHz。它支持2.5 Gb/s的数据速率与脉冲位置调制短距离(10 cm)。采用整流射频前端和相对比较模拟基带的改进非相干接收机,降低了硬件复杂度。
所以,以前的研究主要提出采用高速低分辨率ADC的红外超宽带定位系统,以解决对系统复杂度的要求。但是,随着定位算法的不断发展,人们更多地倾向于采用更先进的算法来实现超宽带技术定位方案。
目标节点的位置可以通过目标节点本身来估计,即自我定位,也可以通过从参考节点收集位置信息的中央单元来估计,即远程定位;为了获得定位节点的准确位置信息,通常在待定位节点和位置已知的多个参考节点(也称为锚节点)之间交换信号。
对于无线定位,有多种方法,它们具有不同程度的精度和准确性。一般情况下,采用的是结合不同参考节点与待定位目标节点之间的距离估计的三角测量法,这个过程就是所谓的两步方法;根据算法的不同,距离测量可以采用不同的信号参数,这些参数或者是延迟,或者是到达时间(ToA,time of arrival);ToA最适合于UWB系统,因为它利用了UWB信号的高时间分辨率[6-8]。
文献[9]针对传统无线定位技术在室内定位精度不高的问题,提出了一种基于UWB技术的室内定位系统。首先,提出了定位服务器与移动端APP实时交互的系统结构,以解决室内移动人员自主定位与导航的问题。其次,在双向测距(TWR, two-way ranging)算法中增加一条无线电信息以减小时钟偏移引起的测距误差,从而提高算法性能;文献[10]提出了单路径模型的Cramer-Rao下界和两步下界定位算法。分析表明,该算法比典型两步法能获得更小的方差。然而,单路径模型并不适用于UWB信道,因为UWB信道存在许多多径分量;尽管密集多径信道的最大似然(ML,maximum-likelihood)一般是已知的[11],但它对于实际实现过于复杂,这也是许多两步定位方案的主要目标成为简化多径模型;文献[12]提出了利用信号分类(USC,use of signal classification)方法和聚焦矩阵(FMs, focusing matrices)。然而,该方案假设多径反射器的数量是已知的,而且它们比接收器的数量要小;在文献[13]中,作者通过将接收信号处理为高斯信号,提出了密集多径信道的ML近似;文献[14]提出利用期望-最大化算法来寻找最大似然,然而,该算法还没有在诸如UWB的密集多径场景中得到验证;文献[15]针对工业现场自动导引运输车(AGV,automatic guided vehicle)定位方式灵活性差的问题,提出了一种超宽带室内定位系统。首先,提出了高效的多基站测距和多标签调度机制,解决标签冲突和组网问题。其次,针对三角形质心算法实际应用中测距极大误差引起的定位精度低和稳定性差的问题,引入可信度概念,提出了内三角形质心算法,通过可信度算子削弱测距极大误差的影响来提高算法性能。
文献[10]的研究表明,典型的两步法是次优的。因为在第一步的不同锚点的测量是独立的,而且忽略了所有测量值必须与单个发射器一致的约束。因此,如果将两个定位步骤合并为一个阶段,然后从每个锚节点接收到的信号直接估计目标位置(DETL, direct estimation of target location),就可以获得更好的性能,特别是在具有挑战性的环景中。
因此,本文首先提出了一种新的定位方法—DETL,提出的方法处理一组测量值或可能的ToA估计量,然后把所有这些测量值用来确定节点位置;由于这种定位方案存在的强多径分量,使得在所有基于阈值(峰值)的ToA估计量中选择合适峰值呈现模糊性,因此,为了克服这个缺陷,提出了基于多ToA的定位方案,同时也使得需要传输到中央节点的数据量大大降低;仿真实验结果表明,提出的定位方案相比于典型的两步定位方案无论是在视距场景还是非视距场景中都具有更高的目标跟踪能力和更小的定位误差累计分布函数。
1 超宽带信号模型
超宽带(UWB)信号模型被视为是一列单位能量高斯脉冲p(t),其持续时间很短,通过M路抽头延迟信道传播,其信道脉冲响应为:
(1)
式中,hm为第m路的脉冲幅度(即第m个脉冲的衰减系数),τm为时延,τ0<τ1<,...<τM-1,τ0是必须估计的ToA。则接收到的信号可表示为:
(2)
式中,Tf为脉冲重复周期,也称为帧周期,w(t)是方差为σ2的零均值白噪声。在频域内,与第k个发射脉冲相关的信号在频域中表示为:
(3)
与移位脉冲相关的频率分量为:
Sk(ω)=P(ω)e-jωkTf
(4)
式中,P(ω)为脉冲p(t) 的傅里叶变换,Vk(ω)为与第k个符号相关的噪声。对式(3)在ωn=ω0n(n=0,1,...,N-1)处采样,其中ω0=2π/N,将频域样本Yk[n]重新排列成向量Yk∈CN×1,并显式分离视距(LoS,line-of-sight)项得到:
(5)
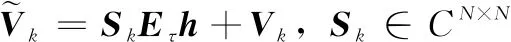
Eτ=[eτ1,...,eτm,...,eτM-1]
(6)
式中,eτm=[1e-jω0τm,...,e-jω0(N-1)τm]T。除h0外,信道衰落系数排列在向量h=[h0,...,hM-1]∈RM-1×1中,噪声样本排列在向量Vk∈CN×1中。
2 基于ToA估计的两步定位方案
一般来说,定位问题分为两个子问题:测量到已知位置的锚节点的距离并通过三边测量法得到位置估计。前者与到达时间(TOA, time of arrival)估计问题高度相关,而后者通常由一个简单的最小二乘(LS, least squares)算法解决。在IR-UWB中也是如此。然而,近年来的研究表明,如果把问题作为一个整体来看待,这种定位方法可能会得到改进,特别是在具有挑战性的情况下。这就是将两步法转换为一步过程,其中将数字化信号组合起来直接求解位置坐标。通常将这种定位方法称为直接位置估计(DPE, direct position estimation);DPE解决了两种不同的定位问题。第一种是由来自于已知位置的不同同步发射机的信号对接收机进行自定位。这就是全球卫星导航系统(GNSS, global navigation satellite system)的情形,其中DPE方法基于最大似然估计(MLE,maximum likelihood estimation)。在这种情况下,与两步法相比,克拉蒙罗界(CRB,cramer-rao bound)具有更高的精度;第二种从已知位置的不同锚节点接收的信号定位一个发射机也可采用DPE解决。在这种情况下,DPE需要将接收到的信号传输到中央处理节点,而两步方法只需要传输估计的参数。然而,标准的两步方法不能解决DPE的性能问题。针对这一问题,可以采用窄带辐射源定位和应用无源定位的DPE方法。
本节首先提出基于ToA的IR-UWB系统的定位方案。本节中提出的估计器是将作为第3节中提出的更复杂的估计器的基础。
在典型的基于ToA的两步定位方案中,位置估计首先通过测量到已知位置的锚节点的距离,然后再执行三边测量法;为了测量距离,ToA估计器是基于计算伪周期图或功率延迟周期图,后者定义为信号能量相对于传播延迟的分布,即:
(7)
式中,l=1,...,NA表示锚指标,上标H表示转置复共轭,Rl为样本协方差矩阵,定义为:
(8)
式中,Nf为观察到的帧数目。ToA估计值是周期图Pl中超过某个阈值r的第一个峰值。阈值的选择是基于阈值判决的所有ToA估计技术中的一个关键因素。对于特定信道的阈值估计存在一些方案,如文献[16]提出了一种基于动态阈值检测的TOA估计算法来提高测距精度并降低算法复杂度。对接收方收到的匹配滤波输出脉冲进行峰值检测,并设定一个能够反映出信号和信道特性的联合度量参数,根据该参数的不同设置相应的最佳阈值因子;文献[17]针对密集多径(DM, dense multipath)信道中采用最大似然(ML,maximum-likelihood)估计在传统均方误差(MSE, mean squared error)和置信边界下基于到达时间的测距的可靠性,提出了一种可靠性和阈值性能联合估计器。结果表明,在DM存在的情况下,ML估计器由于其白化特性使信号主瓣失真,导致带宽(BW,bandwidth)相关的偏差,甚至在离群点驱动的阈值区域之前出现。虽然这种方案提供了联合ML估计和阈值检测估计误差的低复杂度,但它是基于区间估计(MIE,method of interval estimation)方法结合阈值的局部误差预测。所以,这类大多数方案需要对定义阈值级别的一些参数进行校准和启发式调整,这反过来给估计器带来了额外的误差和计算量。
3 软两步法定位方案
3.1 直接估计目标位置的定位方案
直接估计目标位置(DETL,direct estimation of target location)尝试一步求解定位问题,允许直接在空间坐标上执行多维搜索。通过将传播延迟与锚节点和目标节点之间的几何距离联系起来,使联合优化问题成为可能。考虑DETL的动机基于两方面:一方面是关于两步法的ML估计器[18-19]的理论潜在增益,另一方面是克服ToA测距问题所需要的阈值选择问题。正如前面所讨论的,与LoS相关的延迟估计τ0,l是通过寻找高于给定阈值的第一个相对极大值而不是寻找与功率延迟的绝对极大值相关的延迟。基于ToA测量的测距精度很大程度上依赖于阈值的恰当选择,使测距误差最小化的最佳阈值依赖于场景。尽管在更一般的情形下有一些确定阈值的建议,但在实际中,这种选择通常需要一个校准步骤。
采用与基于ToA的两步法定位相同的设置,DETL问题可以构建如下。
将观测频率样本向量定义为从所有锚点接收到的信号的串接,即:
Y=(Y(1),...,Y(l),...,Y(NA))T
(9)
其中:
(10)
为简便起见,去掉符号脉冲指标,根据式(5),则信号模型可以用LoS贡献写为:
(11)
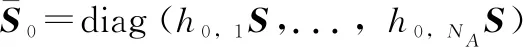
DETL位置估计就是使下列成本函数最大化的位置向量:
(12)
式中,R=YYH。直观地说,该算法所做要的就是用空间坐标来表示周期图,然后将它们相加。
尽管DETL方案有望提供比典型的纯两步方法更好的结果,但DETL方案仍然不是最优的。一方面,在DETL中,误差的主要来源来自这样一个事实,即UWB信道不是典型的LoS场景。在LoS场景中,LoS具有比其他多径分量更强的振幅。事实上,在信道实现中,延迟多径比LoS大得多;另一方面,采用与ToA估计相同的原理求解DETL位置,算法的目标是通过校正与延迟特征向量ep对齐来最大化周期图,由于在每个锚中估计的周期图不是要最大化的函数,而是对第一个峰值感兴趣,因此将这些信号加起来并不是最佳的,因为这样就失去了第一个峰值比强峰值更重要的思想;为此,下面提出一种基于多ToA估计的方案。
3.2 基于多ToA的位置估计方案
3.2.1 算法原理
阈值的选择始终是一个关键因素。我们知道,基于ToA测量的测距精度很大程度上依赖于阈值的选择,如果选择不当,可能会大大降低性能。因此,本节提出解决方案如下:不设置一个阈值并保持第一个峰值在其之上,而是选择全部突出的峰值,然后采用所有潜在的ToAs来找到位置。将所有潜在的ToAs收集在中央处理单元中,并选择使三边测量成本函数最小的ToAs的组合。换句话说,位置估计值就是使以下成本函数最小化:
(13)
式中,k=[k1,...,kl,...,kNA],kl∈(1,...,ml),ml是在第l个锚节点中检测到的峰值数目,τl[kl]是在第l个锚节点中检测到的潜在的第kl个ToA。
然而,并非所有选择的峰值都同样可能是真正的ToA。例如在图1中,最后一个峰值是真正的ToA,这意味着所有前面的峰值都是噪声或该峰值的脉冲旁瓣,这种情况是非常不太可能的。无论怎样,必须在周期图中加入峰值的能量信息和峰值的相对位置。因此,用该峰值为真实ToA的概率来加权每个峰值才是合理的。 通过对峰值加权,提高了位置估计算法的整体性能,因为峰值的数量减少了。因此,最小化成本函数将更变得更容易,而且减少了选择不代表目标位置的路径的概率。
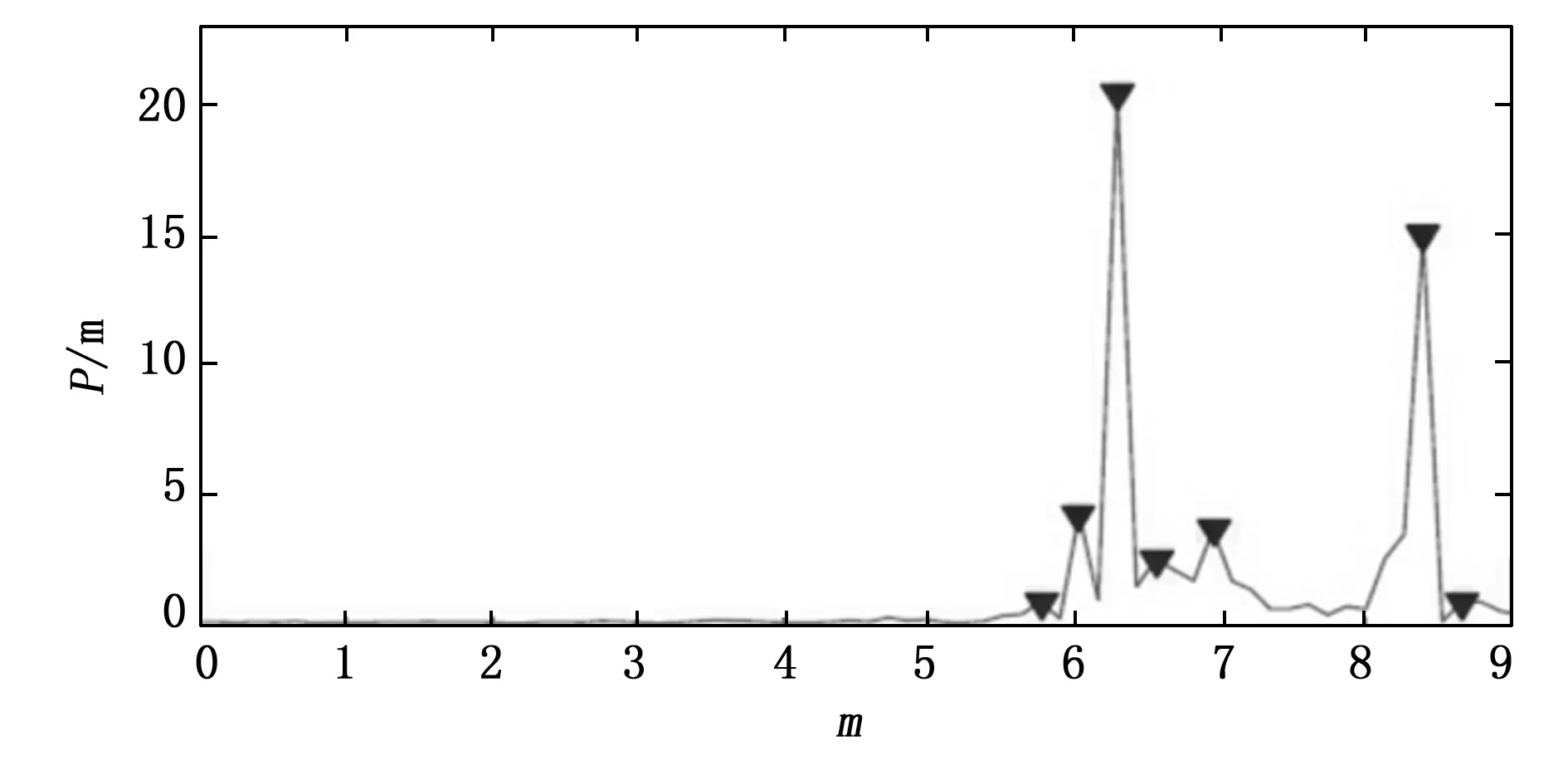
图1 周期图实现
然而,当出现阈值选择时(在纯ToA周期图方法中),寻找这些概率并不是一件容易的事情。因此,下面提出一种加权准则,它是一种基于ToA的能量分布的启发式方法:
(14)
式中,EToA是代表ToA的能量的随机变量(其分布根据经验得到),Wpk0=0,Epki为第i个检测峰值的能量。最后,位置估计为:
(15)
式中,Wl[kl]为第l个信标的kl峰值的权重,参数λ是一致性和延迟概率之间的权衡。
通过采用上述方法,DETL中存在的强多径分量的问题就得到了缓解,因为现在考虑了较早的峰值比较强的峰值更重要,而且峰值是一致的;此外,还解决了出现在两步方法中选择峰值的模糊性,因为两步方法中要选择多个峰值;此外,DETL方案需要将整个信号传输到中央处理节点,而基于多ToA方案只需要传输潜在的ToAs,涉及的数据要少得多。
3.2.2 算法实现
在求解式(15)的成本函数时,必须处理依赖于离散变量(即变量k)的函数。通过枚举所有可能的组合来解决这个离散优化问题是不可行的,因为组合的数量随锚节点的数量呈指数增长。因此,下面提出采用分支定界法[20-21]算法来减少搜索空间。
分支定界法是一种基于树搜索的算法,其中树的每个节点都是一个子问题,在求解一个子问题之后,就可以设定一个关于最终解(树的叶子)可能有多好的界限。如果这个界限比已经得到的解更好,就扩展这个节点并探究它的子节点,否则,就删去该节点,从而减少搜索空间。
从以下内容开始,将把锚节点称为信标,把树的节点称为节点。
在本文的问题中,树的要素为:
1)节点:一种特定的三边测量值,采用的信标比可用的少,树的深度等于信标的数量;
2)下界:该特定三边测量的成本;
3)子节点:给定父节点的子节点是采用与父节点相同的参数但添加新信标的ToA信息的三边测量值,子节点的数量等于通过新信标估计的潜在ToAs的数量;
4)叶子:问题的可能解。叶子的数量和组合的数量一样多。
探索树的方法是快速找到解的关键因素。所提出的方法是最佳优先搜索策略,它通过扩展最有希望的节点来探索树。值得注意的是,尽管最坏情况下分支定界法的复杂度是指数级的,但在实际中,对于本文的研究来说,它是有效的。
算法1所示为所提出的算法实现的伪代码。其中优先级队列PQ是一个队列,队列中的每个元素都有一个相关的优先级(在本文的情形中,界限越低,优先级越高),然后一个具有高优先级的元素先于一个具有低优先级的元素得到服务,TreeNode是一个结构,它存储使用的信标、用于每个信标的潜在的ToA、界限的值和估计的位置,只要这些信标可用。
算法1:位置的计算
定义:优先级队列PO,结构TreeNode
1.任意选择一个信标b1
2.for b1中全部 ToAs do
3. 生成一个TreeNode,即节点node
4. Set node.bound=0
5. Set 其余节点参数
6. 将node放入PQ
7.end for
8.Solution=Ø
9.J=∞
10.while PQ不为Ø do
11. 将PQ的最高优先级节点topNode删除
12. if topNode.bound(J then
13. 探索topNode的子节点
14. 将子节点放入PQ
15. for 全部子节点 do
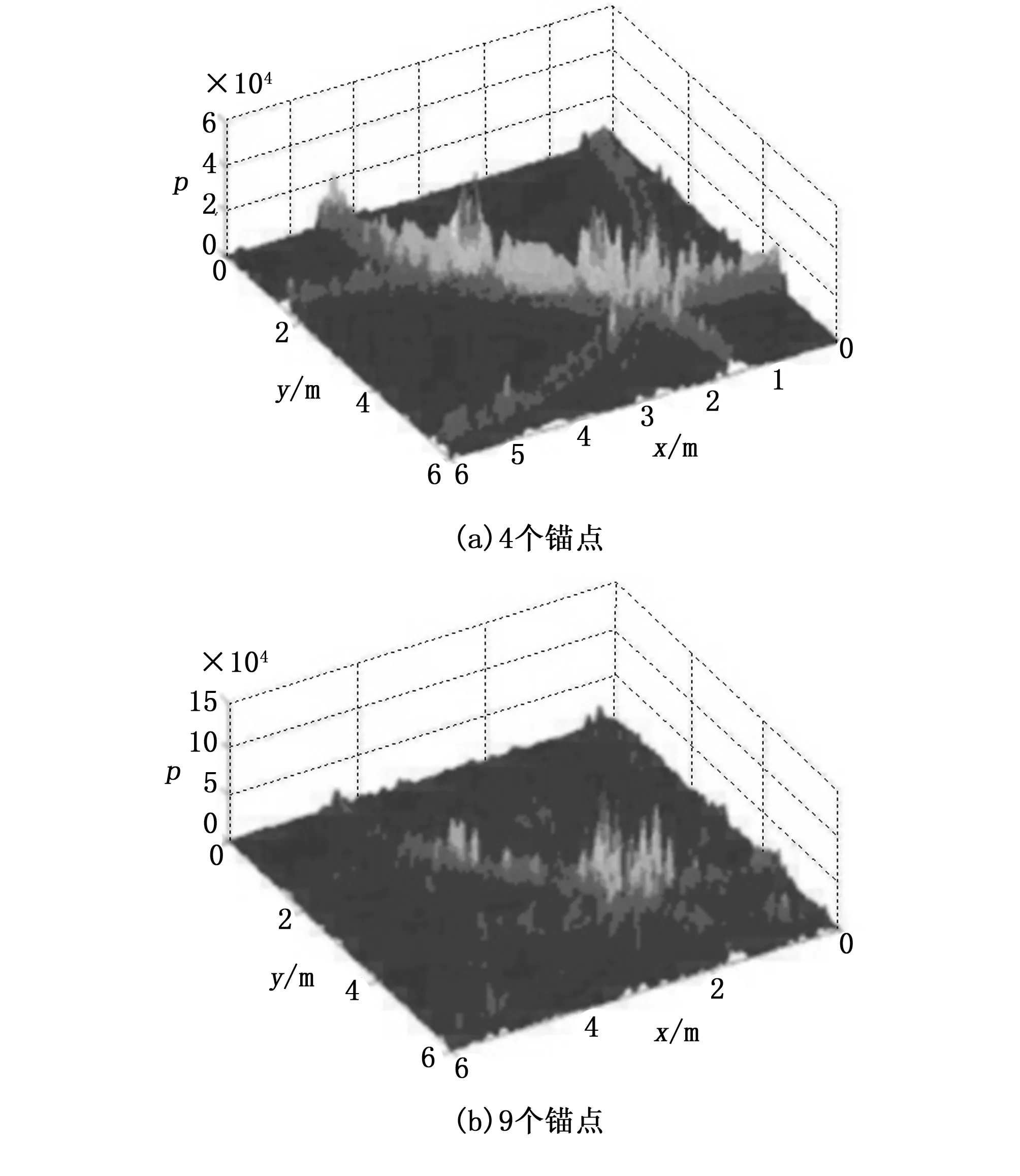
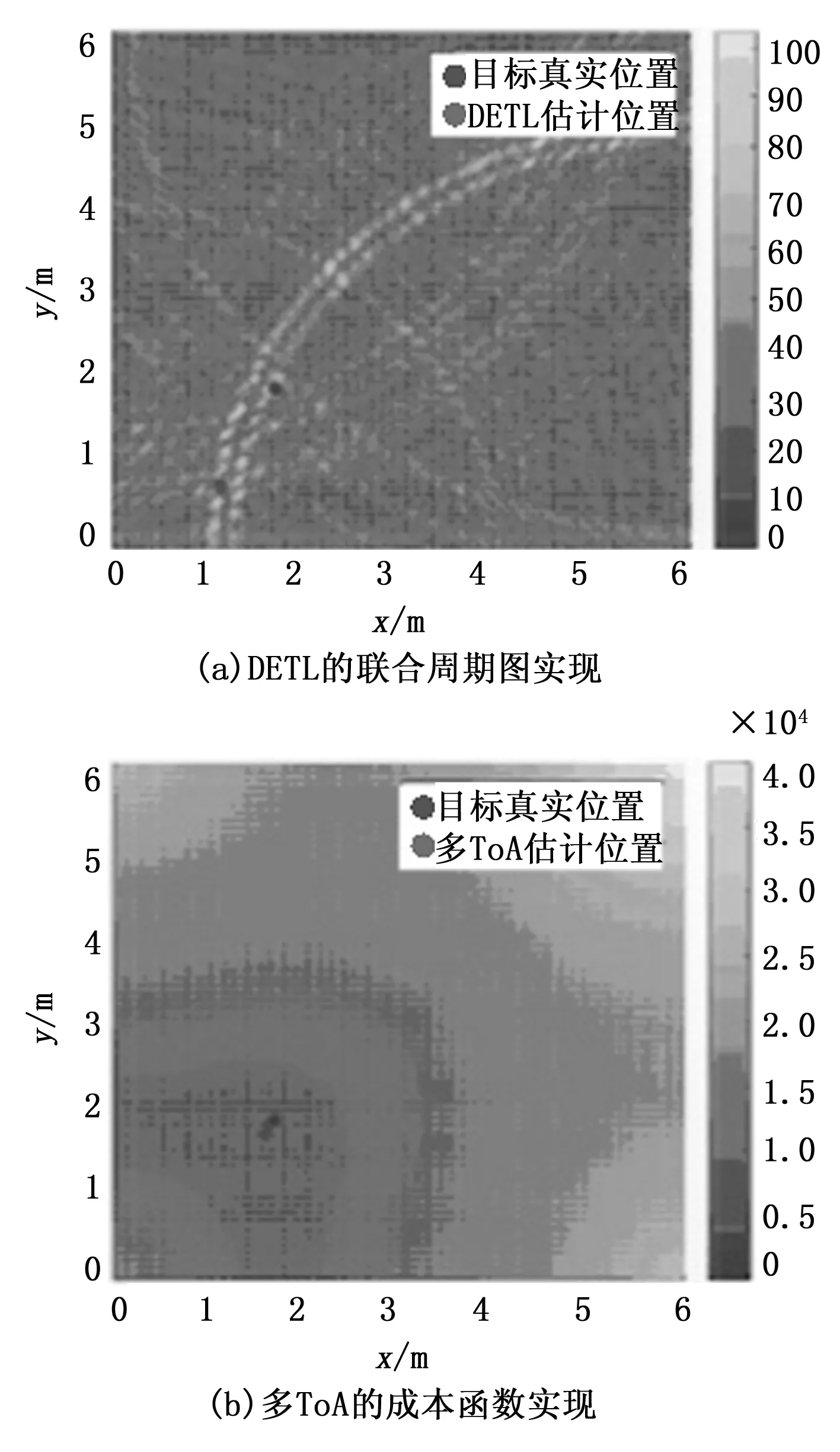
16. if 子节点是树叶且child.bound 17. 更新J 18. Solution=child 19. end if 20. end for 21. end if 22.end while 本节通过采用IEEE802.15.4a UWB信道模型[22]进行数值仿真来评价本文提出方案的性能。具体来说,就是采用CM3办公室LoS和CM4办公室NLoS(非视距)模型,这两种模型都是具有密集多径特征的室内办公环境。仿真设置配置如下:把一个单目标放置在6×6 m2的正方形房间内,并连续发射高斯单周期脉冲,持续时间Tp=1 ns。发射的脉冲由放置在房间角落的信标(锚点)接收;接收到的信号经过低通滤波,以消除混叠,并以2 GHz采样;在所有场景中,对于不同的仿真目标,每个信标的信噪比(signal to noise ratio,SNR)分别设置为-1.2 dB、3.6 dB 和4 dB。 图2所示为CM4办公室NLoS场景下(其中多径效应更为尖锐)的DETP方法的信道实现成本函数式(12)得到的结果。从图2(a)可以看到,当只有4个信标节点时,存在几个振幅相似的局部极大值。减少强多径分量造成的模糊性的就是增加信标节点的数量,如图2(b)所示,可以看到,在目标位置现在只有一个明显的最大值。 图2 在CM4办公室NLOS场景下DETL的周期图实现,其中SNR=4 dB 为了表明作为信噪比函数的性能差异,图3所示给出了在CM3办公室LoS场景下不同信噪比的DETL方法的成本函数实现,其中设置4个锚点。 图3 不同信噪比时在CM3办公室LoS场景中有4个锚点时的DETL方法的周期图实现 图4(a)和(b)所示为采用4个信标节点在CM3 办公室 LoS场景中分别对于DETL和多ToA获得的成本函数式(12)和式(15)得到的结果。如前所述,在UWB信道中,LoS关于多径分量衰减,这可能导致DETL方法错误地估计位置,如在图4(a)中所看到的;然而,多ToA方法不会受这种信道传播特性的影响,并设法正确估计位置,如图4(b)中所看到的。 图4 采用4个信标的目标定位结果 对于位置估计精度的评价,我们考虑了每种场景的500个信道实现。图5为对于CM3办公室LoS和CM4办公室NLoS场景的DETL、多ToA和基于ToA的两步方法的定位误差在累积分布函数(CDF, cumulative distribution function)方面的仿真实验结果。在图5(a)中,还给出了采用严格LoS信道(即LoS总是具有较高能量的信道)时DETL的CDF。在这种情况下,可以看到与其他方法有类似的性能。两条DETP曲线之间的差异表明,它对LoS的强衰减并不稳健,这一点在图5(b)中得到了印证,DETL表现非常差;图5(a)还给出了当阈值偏离最优值30%和40%时两步法的CDF。这些曲线表明了两步法对阈值的敏感性;从图5可以看出,本文提出的多ToA方法优于DETL方法。而且对比图5(a)和图5(b),还可以得出结论,本文所提出的2种方法对于NLoS传播损伤具有较好的鲁棒性。 本文针对红外超宽带定位技术提出了2种新的基于频域信号的直接位置估计方法,并在IEEE 802.15.4a标准组开发的真实信道模型下进行了评价;提出的直接位置估计算法是基于对TOA估计的伪周期图方法的推广,不需要采样的接收信号,且不需要估计信道系数,只需要一组测量值(ToA估计值),从而降低了定位方法的复杂性,而且这种复杂性的降低不会导致定位问题的信息丢失;提出的软两步定位方案相对于一般两步定位法的一个最主要优点是软两步定位方案不需要任何校准,只需要适当的阈值设置,这在实践中可以随着传播条件的变化而变化;此外,数值仿真实验结果表明,提出的方案具有较好的位置估计精度,对NLoS传播具有较好的鲁棒性;下一步的研究将针对合适的权重分析以及对所提出算法的复杂性的解析分析;对于未来的研究,将着重考虑进一步减缓多径效应的研究,以及与考虑与阈值校准的两步法进行更详细的比较。4 仿真实验结果

5 结束语

