基于PSO-BP的磁致伸缩式静力水准系统温度补偿研究

陆俊宇，秦世伟

(上海大学 力学与工程科学学院，上海 200444)

0 引言

沉降监测是工程安全性监测的一个主要指标，在工程风险管控中发挥着重要作用。静力水准系统(HLS, hydrostatic leveling system)利用连通容器原理来测量工程中各监测点位的沉降值，具有测量精度高、抗干扰能力强、结构简单和自动化程度高等优点，因此在建筑地基稳定性评估、基坑变形监测和城市轨道交通结构监测等工程中得到广泛应用[1-3]。然而，相关研究表明外界环境等因素尤其是环境温度会对系统的测量精度造成一定程度影响。

国内外学者们针对温度对HLS测量精度影响及其误差修正进行了大量的分析研究。其中，温度补偿方式常被分为硬件补偿与软件补偿两类。杨宏等[4]使用两套HLS，通过差分方法来减少温度不均匀对测量精度的影响。Tsvetkov等[5]利用压力泵使液体在连通管中循环并传递热量，从而实现温度平衡，有效减少由温度梯度对HLS造成的误差。然而，硬件补偿生产成本较高且补偿效果不明显[6]，很难应用于实际工程中；软件补偿方式因其通用性强、准确度高且成本低，成为了目前主要的温度补偿方式。Jia等[7]根据HLS的工作原理分析了由温度变化引起的误差原因，并基于理论公式对其误差进行修正。还有部分学者单独对静力水准仪内部的液位传感器开展了温度补偿研究，毛君等[8]分析了温度对磁致伸缩液位传感器的影响原因，并使用最小二乘法的多项式拟合方法对传感器进行温度补偿，该方法能够有效消除温度造成的影响。陈韦名等[9]提出了基于Laguerre基函数的液位非线性校正与温度补偿的复合校正模型，将液位测量值和环境温度作函数自变量，利用复合补偿模型的拟合参数计算出实际液位高度。在实际应用中温度因素会从多个方面对HLS造成影响，进而产生误差叠加，若仅对单一特征变量进行建模，会忽略掉误差叠加问题。何晓业等[10]分析了静力水准连通系统中的温度梯度和钵体温度两个影响因素，并分别提出了对应的误差改正方法。陈龙浩等[11]从温度、延迟效应、液体介质等方面分析了HLS测量误差的组成因素，在此基础上建立了简单的线性修正模型。然而，温度对HLS的影响机制复杂，呈现出复杂的非线性关系，现有研究通常采用简单线性回归建立温度补偿模型，难以实现高精度补偿。

目前，神经网络方法因具有较强的自主学习与适应性学习能力，能够处理各类复杂的非线性问题[12-13]，在各类传感器温度补偿中取得了良好效果[14-16]。然而鲜有研究利用神经网络方法对HLS建立温度补偿模型。因此，本文为解决HLS由温度而引起的测量精度误差问题，从HLS系统层面出发，对多个温度误差影响因素进行分析，基于此建立PSO-BP神经网络方法的温度修正模型，并通过试验来验证该温度补偿模型的有效性。

1 磁致伸缩式静力水准系统测量原理

磁致伸缩式静力水准仪主要由储液钵体和磁致伸缩液位传感器组成，其中磁致伸缩式液位传感器由不锈钢测杆、磁环、电子仓和信号电缆组成。静力水准仪的测量是利用两个不同磁场相交时所产生的脉冲信号被检测到的时间差来计算磁环的准确位置，进而计算出钵体中的液位值。通过连通水管将多个静力水准仪连接组成HLS，当容器发生沉降变形时，容器内的液体高度将不可避免地发生变化，根据所有连通容器内液体高度的变化，进而计算求出点位之间的高差及其变化。其工作原理如图1所示。

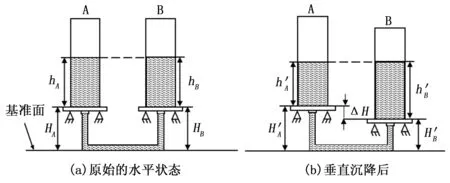
图1 静力水准系统测量原理

如图1所示，h为液位高度，可直接测得；H为测点高程，即静力水准仪钵体内底部到基准面高度。到当系统处于稳定状态时，各钵体液位高度根据帕斯卡定律会始终处于同一水平面，即:

HA+hA=HB+hB

(1)

选定测点A为基准点，当B点相对基准点A产生了沉降ΔH，B点高程发生改变，沉降后的高程为:

(2)

系统稳定后流通液体会重新达到平衡，如图1(b)所示，此时各钵体的液面相对基准面的高度相同，即:

(3)

由式(1)～(3)计算得到B点的沉降变化量为:

(4)

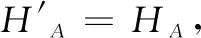
(5)

2 环境温度影响分析

2.1 HLS数据采集

通过测量试验来获取HLS的测量数据与温度数据。本次试验的静力水准仪采用米朗MTL2法兰安装式磁致伸缩液位传感器，量程范围30～150 mm，分辨率≤0.038 mm。实际应用中，HLS存在温度不均匀分布，且试验条件有限，难以对多个静力水准仪完成统一的温度特性标定试验，因此将利用室外自然温度变化进行试验。

位于三层办公楼顶楼的女儿墙内侧布设有6个磁致伸缩式静力水准仪来建立一组HLS，如图2所示。试验过程中静力水准仪需保持静止状态，将其固定在墙体上能够有效避免人为干扰或大风引起的振动，并且在确保该楼周围没有任何能够导致建筑物沉降因素的情况下进行试验。安装连通管应尽量避免与地面直接接触，避免因大气和地面的温度不同而影响连通管中液体。选用水作为流通液体介质，将其均匀、缓慢地注入储液罐，为获得不同液位高度下的采集数据，初始注入液体至钵体高度约60 mm，之后每隔三天加一次水，使水位高度每次上升约30 mm，加水达两次后停止加水，以此便可获得60 mm、90 mm和120 mm三组不同液位高度数据。每个储液钵体上绑有温度传感器来用于采集环境温度数据，将静力水准仪与温度传感器保持数据同步采样，采集频率每小时一次。

图2 磁致伸缩式静力水准系统测量试验

对2021年8月19日到8月22日时间段内监测数据进行分析。输出液位值是由传感器直接读数得到的液位高度，其变化值在图3中以深色曲线显示。如图3所示，可以看出液位变化值呈现先上升后下降的周期性变化趋势，于每日14:00时左右达到上升峰值。由于各测量点位实际并没有发生沉降，认为外界因素仅有温度对HLS产生影响，所以该液位变化应是由温度变化所造成的误差值。进一步分析环境温度随时间的变化趋势(图3中的浅色曲线)，对比可知，温度的变化趋势与误差值的变化趋势一致，由温度变化所引起的液位变化与环境温度呈正相关关系。另外，当监测点与基准点的温度及变化差异不大时，受温度影响产生的误差值近似，使得最终计算沉降的误差偏小；反之，如果两者温度及变化差异较大时，则会导致沉降误差偏大，在实际应用中的沉降数据会处于波动状态。因此，理论上先对HLS中各测量点液位值进行温度补偿，将受到的温度影响消除，再计算其沉降值便能获得更加稳定且准确的沉降数据。

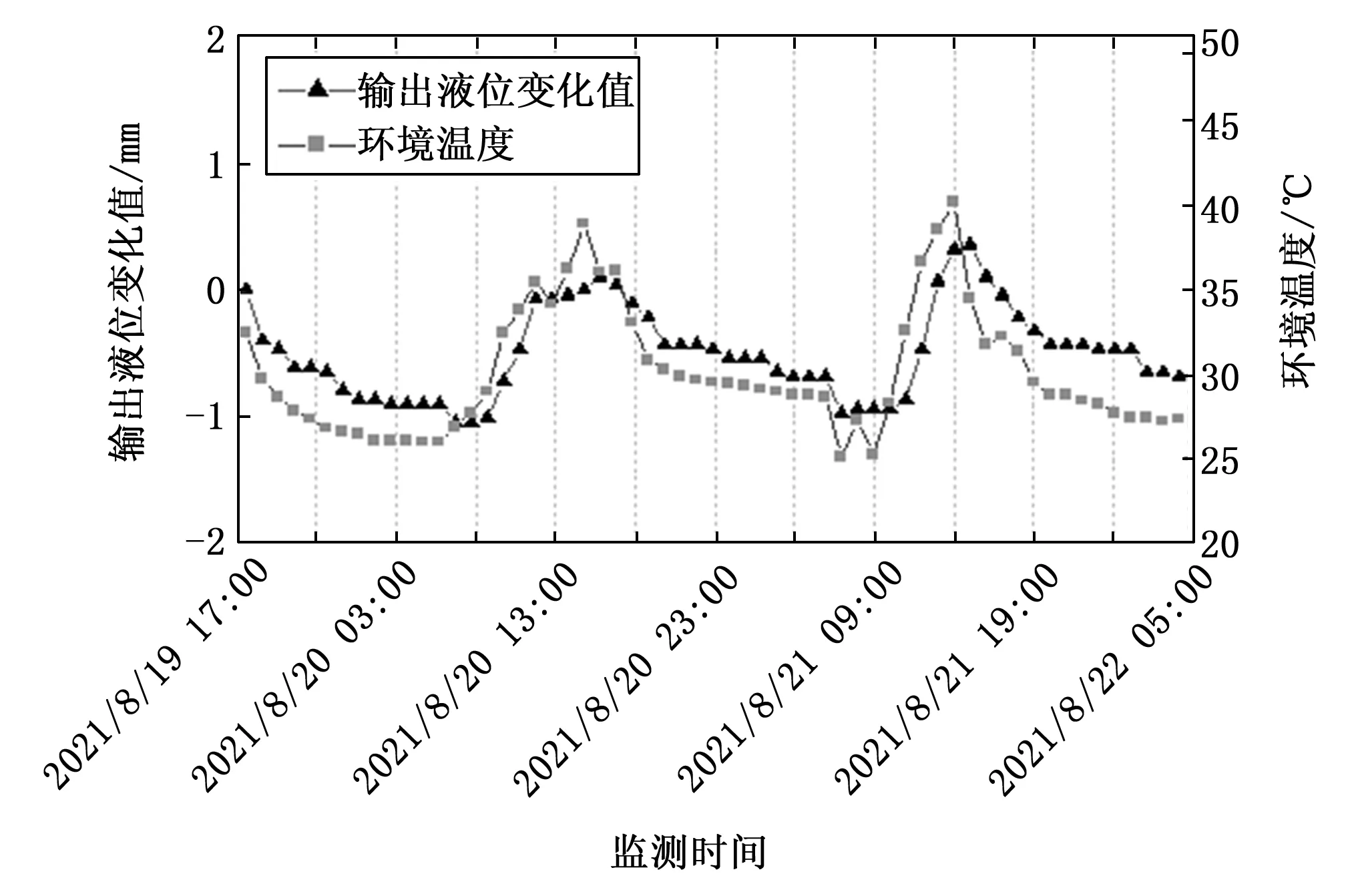
图3 输出液位变化值与环境温度数据

2.2 温度误差机理分析

在HLS测量过程中，环境温度会对液体介质、传感器零部件和连通系统等系统要素造成不同程度影响，进而共同造成了对整个系统的测量误差。根据误差组成结构将HLS中温度造成液位值偏差的因素可分为温度、温度变化率以及温度梯度3种影响因素，具体分析如下：

1)温度对HLS的影响。静力水准仪磁环位置是由测量时的两段脉冲信号时间差计算得到，因此时钟晶振是影响仪器测量精度的重要因素，若液体介质的温度变化较大时，晶振会产生温度漂移，进而造成一定的测量误差[17]。另外，温度变化会引起液体密度的改变，中午气温升高，液体介质膨胀，使液面高度上升；傍晚气温降低，液体介质收缩，使液面高度下降[18]。液位变化会直接磁环位置，从而影响传感器读数的准确性。由此可知，温度会对静力水准仪的输出液位值产生直接影响，可以利用温度值对液位值进行修正，初步确定钵体液位值的温度补偿模型为：

(6)

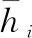
2)温度变化速率对HLS的影响。当环境温度变化过快时，钵体内液体的吸热或放热需要一段时间，导致每次测量时，环境温度与流通液体温度因滞后不同步而存在一定偏差，此刻的环境温度并不能代表液体温度，若以该温度值进行温度补偿计算会导致效果不佳[19]。因此，可通过温度变化速率来近似反映t时刻前的温度值，对液位值进一步修正：

(7)

式中，ΔT为钵体t时刻的温度变化速率。

3)温度梯度对HLS的影响。若HLS中各点位温度及其变化率相同，液体密度改变对计算沉降不会产生影响，然而实际应用中整个系统经常会出现温度的不均匀分布现象。仍然以图1为例，由伯努利方程可知：

pA+ρAgAzA=pB+ρBgBzB=C

(8)

式中，pA、pB为钵体中的大气压强；gA、gB为重力加速度；zA、zB为液面相对高程；ρA、ρB为液体密度。这里认为同一系统下的压强和重力加速度相同，则有：

ρAzA=ρBzB=C

(9)

由于系统存在着温度梯度，导致各钵体中的液体密度不同，ρA≠ρB；进而使两个钵体的液面高度存在差异Δz=zB-zA，并且该误差将分配到监测点液位值上。因此，需要对监测点与基准点之间温度差引起的误差进行消除，最终确定钵体液位值的温度补偿模型为：

(10)

式中，T0为基准点钵体t时刻温度，当计算点为基准点时，T=T0，将不考虑温度梯度影响。

综上可知，叠加以上多个影响因素引起的误差，很难通过理论计算求出精确的误差修正公式。而神经网络方法能够利用非线性逼近方式来反映出不同特征之间的复杂关系，因此可利用该方法对HLS各钵体液位值进行温度补偿。

3 粒子群优化BP神经网络模型

3.1 反向传播神经网络

反向传播神经网络(BPNN,back propagation neural network)，简称BP神经网络，是一种多层前馈监督学习型神经网络，按输入层、隐藏层和输出层将多个神经元节点联结在一起组合而成，具有较强的非线性函数拟合能力[20]。神经网络方法的学习目的是寻找实际液位值与输出液位值、温度、温度变化率及温度梯度之间关系，由算法自动调整并确定各项因素权重，最终对真实液位值做出近似拟合。因此，将输出液位值与各温度误差影响因素在网络结构上构成输入层，实际液位值构成输出层，复杂的分析和中间的校正过程构成隐藏层。其模型结构如图4所示。

图4 BP神经网络模型结构

BP神经网络计算依次分为前向传播和反向传播两个阶段，不断迭代这两个步骤，对网络中的权值与阈值参数更新，目的是使神经网络的目标误差损失最小，得到指定迭代次数内的最优模型。具体计算方法如下：

1)前向传播过程。从输入层依次向前计算到最后的输出层，由此建立网络的输入-输出映射关系。其中，对网络的每一层输入值和网络参数进行线性计算，然后利用激活函数实现非线性映射得到该层的输出值。每一层上单个神经元的前向计算过程为：

(11)

xj=f(Sj)

(12)

式中，i、j分别为网络前一层和当前层的神经元节点；wij为神经元节点i、j之间连接的权值，bj为j节点的阈值；xi是由前一层神经元传递过来的输入值；f为激活函数，常取sigmoid函数或tanh函数；xj为当前神经元的输出值，也将作为下一层神经元的输入。

2)反向传播过程。当前向传播过程到网络的最后一层时，再从输出层反方向折回计算每一层神经元误差，进行参数更新。由输出层计算输出的结果为dj，定义模型的损失函数为:

(13)

损失函数值反映了真实液位值与模型拟合输出值的差异程度，为了减小该差异，根据梯度下降方法在网络层中反向更新模型的网络参数，对于节点i、j间的权值和节点j的阈值调整有：

(14)

(15)

式中，η为模型的超参数学习率，决定了每次更新对网络参数的调整幅度。定义激活函数为sigmoid函数：

(16)

对激活函数求导，得到:

f′(x)=f(x)[1-f(x)]

(17)

进一步计算得到权值wij和阈值bj的导数为:

(18)

(19)

其中:

δij=(dj-yj)·f(Sj)[1-f(Sj)]

(20)

根据上述公式计算，对网络中每个权值和阀值最终按如下公式进行更新。

wij=wij-η1·δij·xi

(21)

bj=bj-η2·δij

(22)

3.2 粒子群优化算法

粒子群优化算法(PSO，particle swarm optimization)是一种基于群体合作的随机搜索算法。该算法利用无质量的抽象粒子来模拟鸟群中的单体，通过多次交互共享信息来更新每个粒子特有属性，从而寻找全局最优解。粒子群算法实现简单，具有良好鲁棒性，易于与其他算法结合以优化算法性能[21]，因此在神经网络训练、模糊系统控制等应用领域得到广泛应用。

粒子具有速度V和位置X两个特有属性，速度代表粒子移动时的快慢，位置代表粒子的移动方向，该算法通过跟踪个体极值与全局极值来寻找粒子的个体和群体最优解。初始化粒子群参数和定义适应度函数后，在每次迭代过程中对计算得到的适应度值进行判断是否更新个体极值和全局极值，迭代至条件满足后输出目标最优解。更新速度和位置的公式为：

Vi=ωVi+C1random(0,1)(Pi-Xi)+

C2random(0,1)(Pg-Xi)

(23)

Xi=Xi+Vi

(24)

式中，Pi表示第i个粒子的个体最佳位置，Pg表示从先前迭代的所有粒子中获得的群体最佳位置，ω为惯性权重因子，通过调整ω的大小，可以对全局寻优和局部寻优进行性能调整，其数值与全局优化性能正相关，与局部优化性能负相关。C1和C2为学习因子，前者反映粒子的自我学习，后者反映粒子的社会学习能力。random(0,1)表示区间[0,1]上均匀分布的随机数。

3.3 PSO-BP神经网络模型

PSO算法能够在更大的解空间内进行搜索，将其用于BP神经网络的参数优化，能够弥补神经网络容易陷入局部最优解、收敛速度慢的缺陷，进而提高BP神经网络算法的拟合准确度与泛化能力[22-23]。因此，本文将使用PSO算法对BP神经网络进行优化处理，优化后的温度补偿模型具体实现步骤如下：

1)将神经网络各层的连接权值矩阵W和阈值矩阵B编码成为粒子，作为粒子群优化中粒子的位置向量，并对其参数进行随机初始化。

2)将神经网络的损失函数作为适应度函数g(x)，则粒子适应度值为使用该组网络参数时的输出值均方误差，粒子群体极值为目标函数的计算最优值。根据式(23)和式(24)来更新种群粒子的速度与位置，在每次迭代中计算每个粒子适应度值Pi，一旦适应度值大于群体极值Pg，则将其替换，最终在预设迭代次数内搜寻到网络的最优权值和阈值。

3)将优化后的最优初始权值和阈值以及样本的输入、输出值一并代入到BP神经网络中进行训练。

4)BP神经网络通过误差反向传播方式进行迭代计算并更新参数。利用损失函数来度量模型输出值与实际液位值之间的差异程度，根据损失值在反向传播过程中确定梯度下降方向并对网络参数进行更新。当其满足终止条件时，结束训练并输出最终的温度补偿模型。

基于PSO-BP算法对静力水准系统钵体液位值温度补偿的具体流程如图5所示。

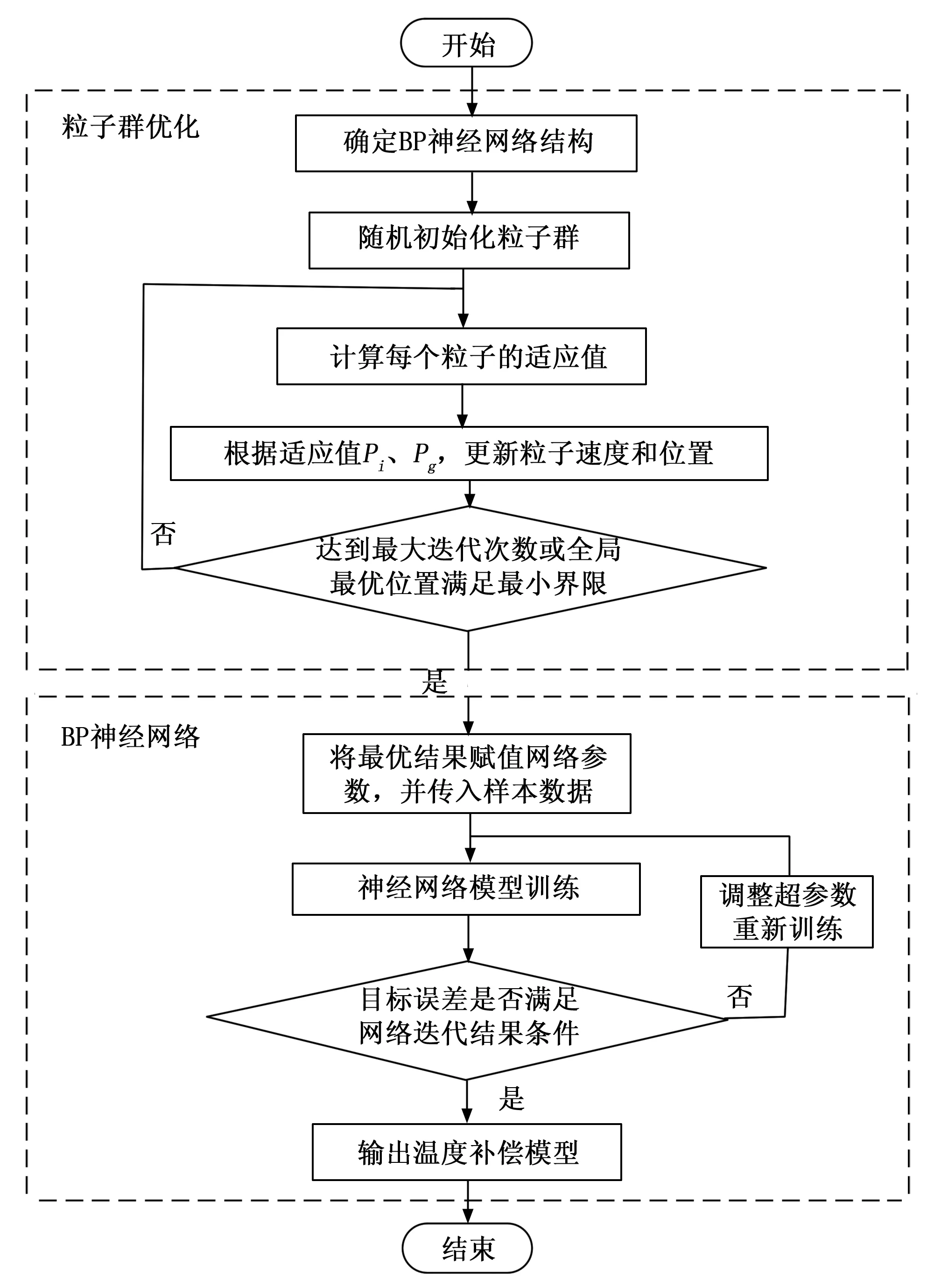
图5 基于PSO-BP的温度补偿流程图

3.4 模型参数设置

通过设置各层神经元个数来确定模型结构。根据本文所确定的温度补偿模型，定义输出液位值X、温度T、温度变化率ΔT和温度梯度T-T0作为模型输入层，即输入层神经元个数n=4；设置两层隐藏层，通过多次测试后确定第一层4个节点，第二层3个节点，即隐藏层神经元总个数j=7；钵体的实际液位值Y作为输出，即输出层神经元个数m=1；以上权值和阈值参数初始化后将得到大小分别为4×4、3×4、1×3的W1、W2、W3和4×1、3×1、1×1的B1、B2、B3参数矩阵，将其转换为一维数组作为初始粒子种群。模型初始学习率设为0.01，迭代次数epoch设为100，使用均方误差(MSE)作模型的损失函数。

4 温度补偿结果及分析

HLS测量试验有F0～F4五个测量点，安置于东侧阴凉处测点F0作为本组基准点，其余作为监测点，数据采集时间从2021年8月19日到8月29日共计十天，数据样本239条。首先对F0监测数据进行温度补偿，将数据集以3:1比例划分为测试集与训练集，应用于PSO-BP神经网络模型中计算。为了对比单个和多个的温度误差影响因素对系统影响，本研究分别建立温度影响因素的单变量和温度、温度变化速率以及温度梯度影响因素的多变量温度补偿模型来进行对比分析。测点F0补偿前后的液位变化值如图6所示。

图6 基准点F0温度补偿前后液位变化值对比

如图6可知，补偿前液位误差峰值达1.09 mm，该误差程度对实际工程监测会造成一定影响。单变量补偿后的均方误差为0.18 mm，误差范围保持在±0.38 mm以内，相比于补偿前均方误差减少75.2%，最大误差减少65.7%；多变量补偿后的均方误差为0.06 mm，误差范围保持在±0.17 mm以内，相比于补偿前均方误差减少91.3%，最大误差减少约83.2%。经过算法补偿过后基本消除了环境温度对测量结果造成的误差。

利用PSO-BP算法对其他监测点进行温度补偿，各测点补偿前后液位变化如图7所示。测点F1到F4经过单变量补偿后的均方误差和最大误差分别降低76.3%、82.7%、76.9%、80.8%和75.2%、62.1%、63.0%、73.0%；多变量补偿后的均方误差和最大误差分别降低85.1%、87.5%、85.0%、90.1%和86.2%、79.6%、77.3%、87.9%。结果表明，温度影响因素占HLS液位误差影响的主要部分，考虑温度变化速率和温度梯度变量的补偿效果会更优于单一温度变量补偿，并且变化曲线更为平滑。

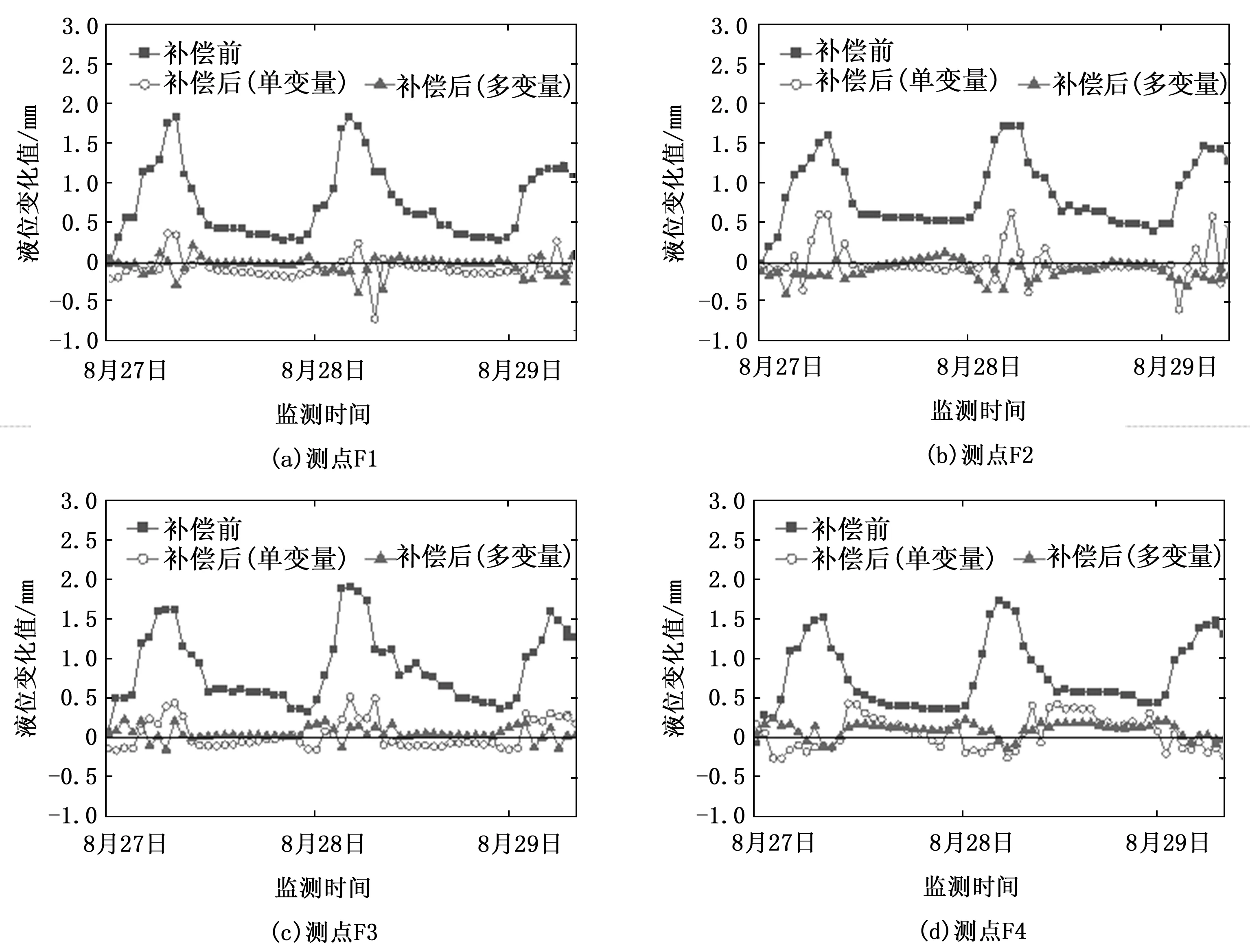
图7 多个测点温度补偿前后液位变化值对比

将温度补偿后得到的修正液位值根据式(5)计算出各监测点位的修正沉降值，沉降误差结果如表1所示。由表可知，HLS经过温度补偿后的计算沉降误差得到有效降低，并且考虑了多个温度误差影响因素的PSO-BP温度补偿模型的消除误差效果要优于单一因素的补偿模型，从而提高HLS测量精度，证明了该模型的可行性。

表1 温度补偿前后沉降误差结果

5 结束语

本文通过HLS测量试验，确定了钵体液位值误差随环境温度变化规律，并对HLS的温度误差影响因素进行分析。在此基础上，利用PSO-BP神经网络算法对HLS建立温度补偿模型，得到如下结论：

1)HLS系统测量精度会受到温度、温度变化率以及温度梯度3个误差影响因素共同影响。基于以上三者构建的温度补偿模型考虑了连通系统各钵体之间的相互影响，其补偿结果优于仅考虑温度影响因素的补偿模型。

2)基于多个影响因素建立的PSO-BP温度补偿模型对静力水准仪液位值的均方误差和最大误差平均降低80%以上，误差降低效果显著，极大程度地消除了环境温度变化造成的误差影响，进而减少计算沉降值误差，提高HLS测量精度。可以为实际工程中的HLS沉降误差修正提供参考依据。