基于半镜面靶标的无重叠视域相机全局标定
段心怡,杨 剑,程泽会
(中北大学 软件学院,太原 030051)
0 引言
在过去几十年,随着计算机视觉在无人驾驶、智能监控、视觉分析等方面的快速发展以及视觉系统成本的降低,多相机视觉系统得到了日益广泛的应用。由于单相机视觉系统存在视场范围狭窄以及无法产生视差等限制,使得其应用受限,因此多相机系统应运而生。同时环境条件限制、设计需求、成本限制等因素的影响,多相机视觉系统往往存在相机之间无重叠视场的情况,然而相机之间的坐标系变换对于很多应用至关重要,例如:视觉测量[1-5]、轨迹追踪[6-9]、自主机器人[10-12]、监控[13-15]等等,因此针对无重叠视场的多相机视觉系统全局标定问题,研究一种高精度、易操作、低成本的有效方法成为很多研究者关注的问题。
相机的全局标定方法是解决局部的相机坐标系转换到全局坐标系的问题,目前针对该问题,研究人员已经提出了多种方法,可分为基于周围环境信息的手眼标定方法[16-20]和基于关联靶标的外参标定方法[21-26]。然而无重叠视场的多相机系统全局标定问题依然是一个具有挑战性的问题,尤其在相机之间的视场无法通视或单向观测的情况下。针对该问题,本文提出了基于半镜面平面靶标的全局标定方法,通过平面靶标的镜面部分将点激光器的光线反射到其他相机的视场内,利用平面靶标的标志点计算靶标的空间参数并得到反射光线的空间方程,最后利用激光光线的方向向量构建相机间坐标系转换方程组,从而确定转换矩阵和平移向量。实验表明所提方法可有效的解算全局标定矩阵,并具有高精度、计算简便、操作简便、设备简单等优点。
1 相关工作
为了解决无重叠视场的多相机系统全局标定问题,科研工作者已经给出很多方法,其可总体分为:基于人工或周围环境信息的手眼或自标定方法[16-20]和基于关联标定物的外参标定方法[21-34]。
自标定方法通常需要设定相机组一定规律的运动。受手眼标定方法的启发,Esquivel等[16]基于每个相机时间同步性估计彼此之间的相对姿态。F.Pagel[17]则给出了运动调整的方法,利用测距法计算相机之间彼此的运动幅度,从而估计相机之间的外参数。文献[18-19]则是在现有的手眼标定等方法基础上,借助加速度传感器和角度传感器等设备进一步优化相机外参的标定,文献[20]则是首先利用SLAM设备(如深度相机)将周围环境进行三维建模,在相机组运动过程中,根据周围环境的三维坐标确定外参。该类方法具有较好的自主性,但也存在计算复杂,精度难以保证等问题。
基于关联标定物的外参标定方法通常不需要相机做特定的运行。针对无重叠视场的多相机系统全局标定问题,文献[21]利用近景摄影测量的原理,首先在室内环境中布置编码点,然后,利用测量设备测量编码点的全局三维坐标,最后利用这些测定的三维坐标点标定相机之间的转换矩阵。文献[22-23]采用经纬仪或激光雷达关联两个相机平面靶标,实现全局标定。文献[24-25]则设计了长距离的链接杆,在长杆的两头分别固定标定靶标,从而实现标定靶的关联。同时有很多科研工作者利用镜面的反射效果,反视另一个相机的视场,从而实现相机的关联[26-30],该类方法简单直接,但需要视场没有遮挡,同时反射后靶标变小,有损精度,利用球面镜反射虽可获得较好的视野,但也存在畸变的问题。Liu等[31]则将激光器产生的光平面投射到平面靶标上,利用光平面的法向量构建相机之间的转换方程。该方法不需要昂贵的设备,具有实施简单的优点,但也存在计算复杂,标定板朝向限制的不足。文献[32-34]中,则进一步提出更实用的方法,利用点激光器产生激光射线,分别在各自视场内截断射线,观测散斑点像,从而计算射线的方向向量,然后利用射线的方向向量构建外参解算方程。以激光射线为靶标的相机标定方法,具有设备简单、实施方便、计算简单等优点,但需要其相机之间的视场可以通视,没有遮挡,并要求单向性观测。
本文所提出的基于半镜面平面靶标的无重叠视域多相机全局标定方法,基于点激光器的射线方向向量约束相机之间的转换方程,并利用半镜面平面靶标改变其光路。该方法具有很好的灵活性,设备简单、易操作、计算简单,由于激光的准直性,精度不受相机布局远近的影响,适用于各种相机布局,在相机之间的视场无法通视或单向观测的情况下依然适用。
2 全局标定方法的原理
基于半镜面平面靶标的无重叠视域多相机全局标定方法的原理如图1所示,不失一般性,图以双相机组为例进行说明, 多相机系统可转化为两两分组的问题。
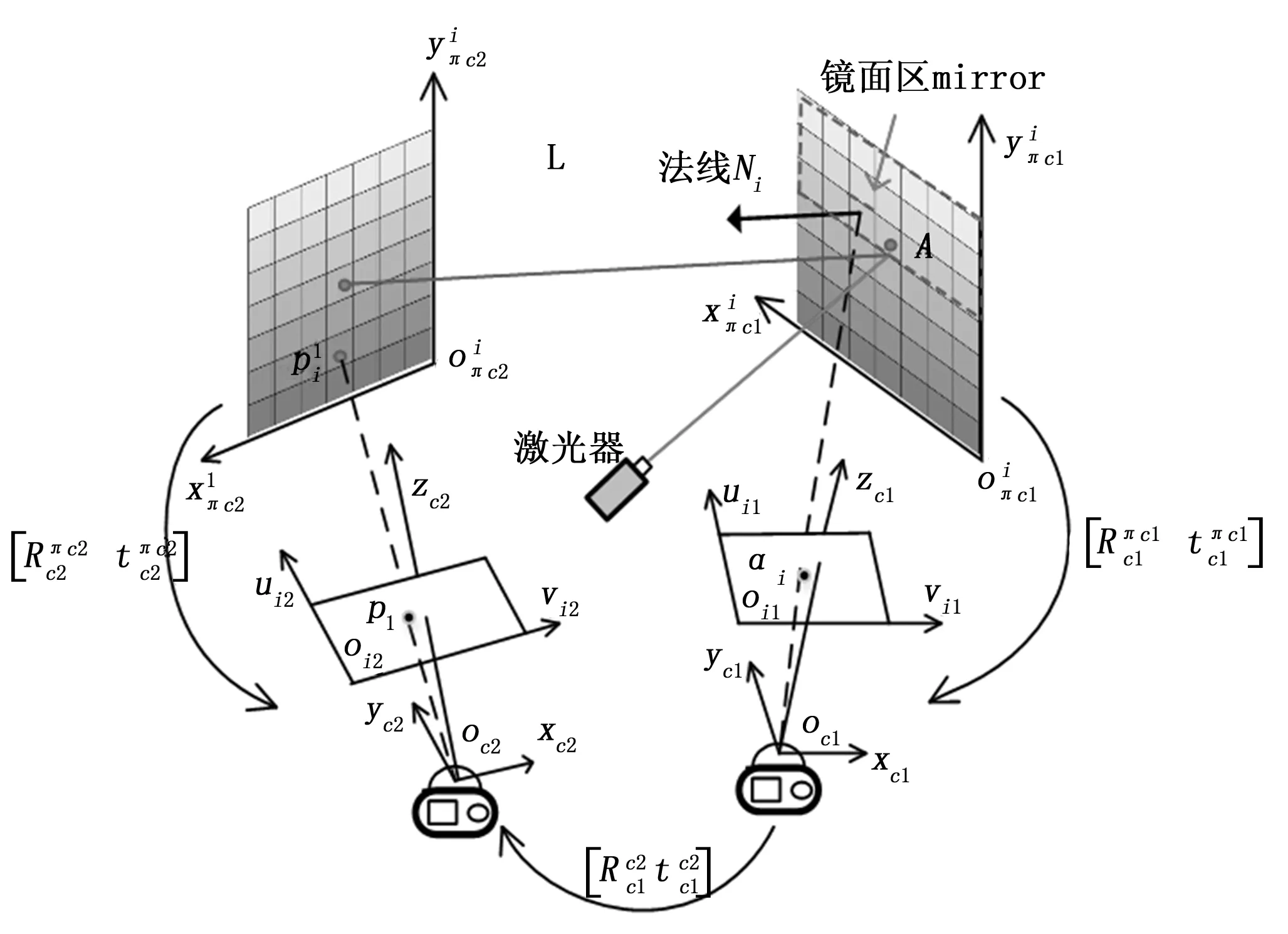
图1 无重叠视域多相机全局标定方法的示意图
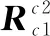
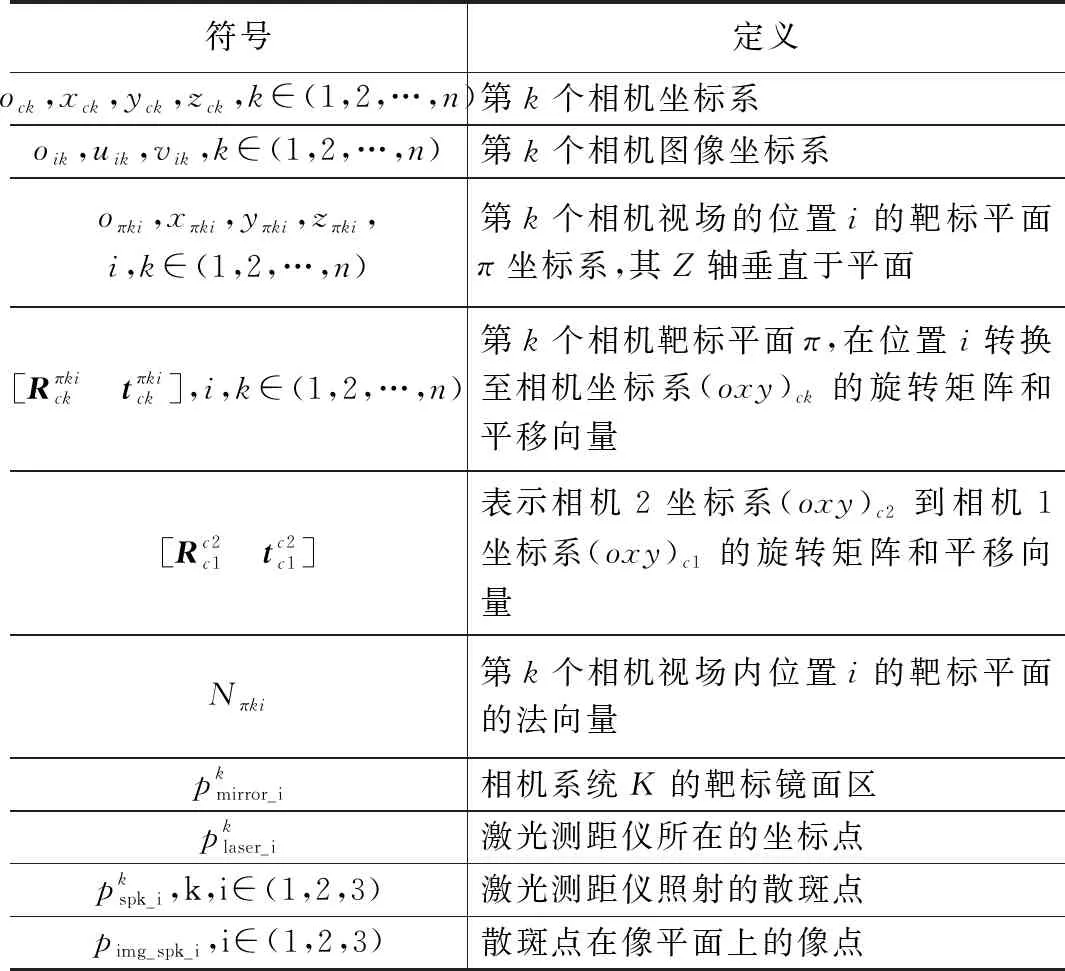
表1 符号与定义
本文所提方法的主要步骤如下:
1)基于张正友[35]的经典标定方法,实现单个相机的内参数的标定Ack,(k=1,2)及相机1,2的自身坐标系外参。
2)将相机群分为两两一组,如图1所示,选定单点激光器的位置;
3)在相机1的视场内,三次移动标定板,则可拦截激光的散斑点A,B,C,并采集图像点a,b,c,则根据3.1小节中的方法可计算得到激光射线的消隐点;
4)在相机c1的视场内,放置半镜面标定板,将激光光路反射到相机c2的视场内,并在c2不同位置截获激光射线的散斑点D,E,F,并采集图像点d,e,f。利用3.1小节中的方法可计算得到激光射线的消隐点;
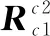
2.1 计算图像消隐点坐标
如图1所示,选定激光器的位置,在相机c1的视场内移动平面靶标,分别在位置i=1,2,3拦截激光射线形成散斑点A,B,C,并采集像点(ai,bi,ci),其结果如图2所示,V∞表示激光射线在相机c1坐标系下的无限远点,相应的vi1∞则表示该无限远点在图像坐标系下的消隐点坐标。
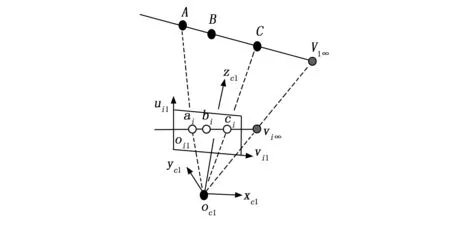
图2 点A,B,C,V∞的交比示意图
(1)
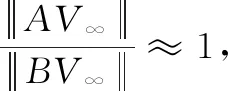
则根据射影几何的交比不变性[34]可估算图像消隐点vi∞1:
(2)
公式(2)中,(ai,bi,ci,vi∞1)表示激光射线散斑点(A,B,C,V1∞)的单应图像点,其坐标系如图2所示。同理,经过半镜面平面靶的反射,光线进入相机c2的视场内,移动平面靶可截取激光的散斑点图像(di,ei,fi,vi∞2),基于交比不变性可估算反射后光线的消隐点vi∞2。
2.2 基于半镜面的法向量及消隐点计算R21
线的消隐点表示了直线的方向向量。设dci,(i=1,2)表示激光射线的方向向量,如图3所示。根据2.1节计算的消隐点可得射线的方向向量(3):
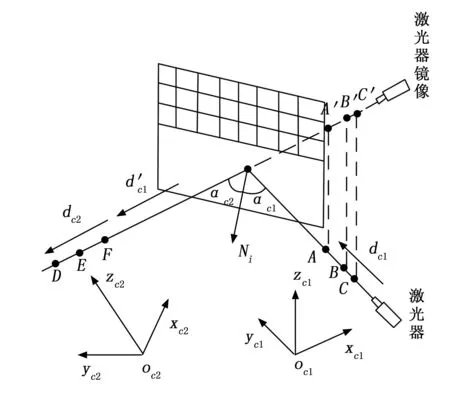
图3 半镜面平面靶反射激光光路
(3)
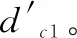
(4)
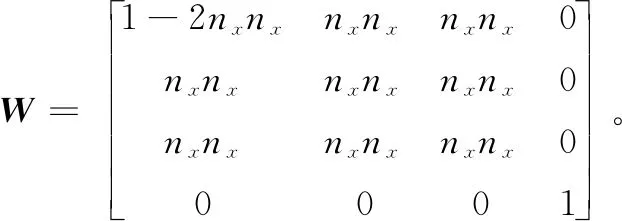
因此根据式(3)和(4)可知,经过镜面反射后,入射光线与反射光线的消隐点之间的关系式:
(5)
根据射影几何可知,设空间中一点在两个相机像平面上的坐标为mc1和mc2,其关系可用单应矩阵H表示为:
mc1=Hmc2
(6)
当单应平面为无穷远平面π∞,其关系依然存在,此时像点为无穷远点的像,也就是图像的消隐点。
(7)
结合式(5)可得到:
vi∞1=W-1H∞vi∞2
(8)
根据文中的设定,第一个摄像机c1的坐标系为全局坐标系,经过标定后,其两个相机内参已知,相机矩阵分别为:
(9)
对于单应平面π上的任一个点M, 考虑它在两个摄像机下的投影。显然,在第一个摄像机下的投影为:
(10)
因此,单应平面π到第一个像平面的单应矩阵为H1=Ac1。在第二个摄像机下的投影为:
(11)
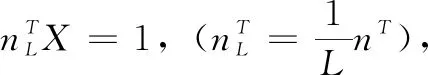
(12)
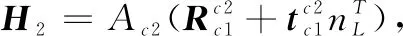
(13)
当单应平面π变成无穷远平面,所以在式(13)中取L→∞的极限值,可得到无穷远单应矩阵,显然:
(14)
因此:
(15)
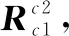
2.3 计算平移向量
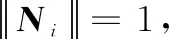
(16)
设点A,B,C的镜像点表示为A′,B′,C′,根据式(16)可得:
A′,B′,C′=QA,QB,QC
(17)
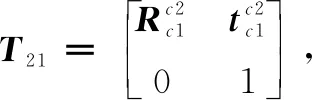
设D点在相机2下的坐标为Dc2=(xDc2,yDc2,zDc2),坐标转化为相机1坐标系后Dc1=(xDc1,yDc1,zDc1),其转换关系如下:
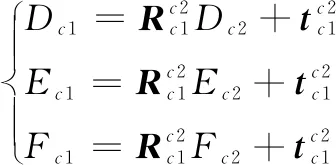
(18)
同样的坐标表达方式及转换关系可用于A,B,C,D,E,F。
A,B,C做镜面对称得到A′,B′,C′,D,E,F共线,因此可得:
(19)
可写为:
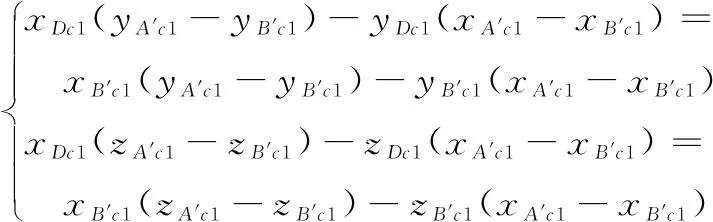
(20)
把式(18)代入到式(20)可得:
(21)
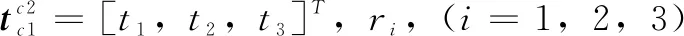
2.4 非线性优化
如图3所示,设激光线在位置i的方程为Li,其可表示为如下方程:
(22)
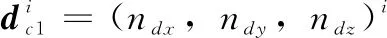
通常认为,相机CCD图像噪声符合高斯分布,采用最大似然法针对下式求解最优解可获得最小误差的相机外参。
(23)
其中:α=(T2,nxi,nyi,nzi,xi0,yi0,zi0),m表示点激光器的位置,d(qij,Li)则表示点qij偏离直线Li的距离。同时这里采用了Levenberg-Marquardt算法作为优化方法,实现对最小二乘结果的最优解。
3 实验部分与分析
3.1 综合仿真实验
为了验证所提算法的有效性和精度,设计了如下的实验部分,分析了影响标定精确性的3个主要的因素:1)图像噪声对激光散斑中心点检测精度及镜面法向量计算精度的影响;2)相机之间的距离对全局标定的影响;3)布置激光器的数量对相机全局标定参数的影响;
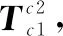
3.1.1 相机图像噪声
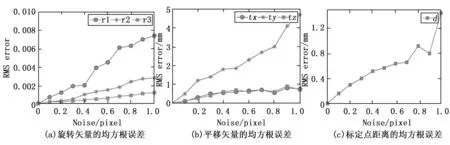
图4 图像噪声对标定点的误差影响
由图4 可以看出,所有相机外参数的均方根误差随着噪声水平线性增长。通常在真实实验中,会采用工业相机,其图像的噪声要小于0.2个像素。
同时采用的点激光器射线强度符合高斯分布,因此基于Matlab仿真了光强高斯分布的光斑图像,并分别进行100次的添加高斯白噪声后,拟合高斯分布的中心点,其中心点偏离的RMS结果如图5所示。可以看出,在标定板方向向量与激光射线方向向量夹角<10度,图像噪声<1个像素的条件下,其RMS小于0.006 mm。
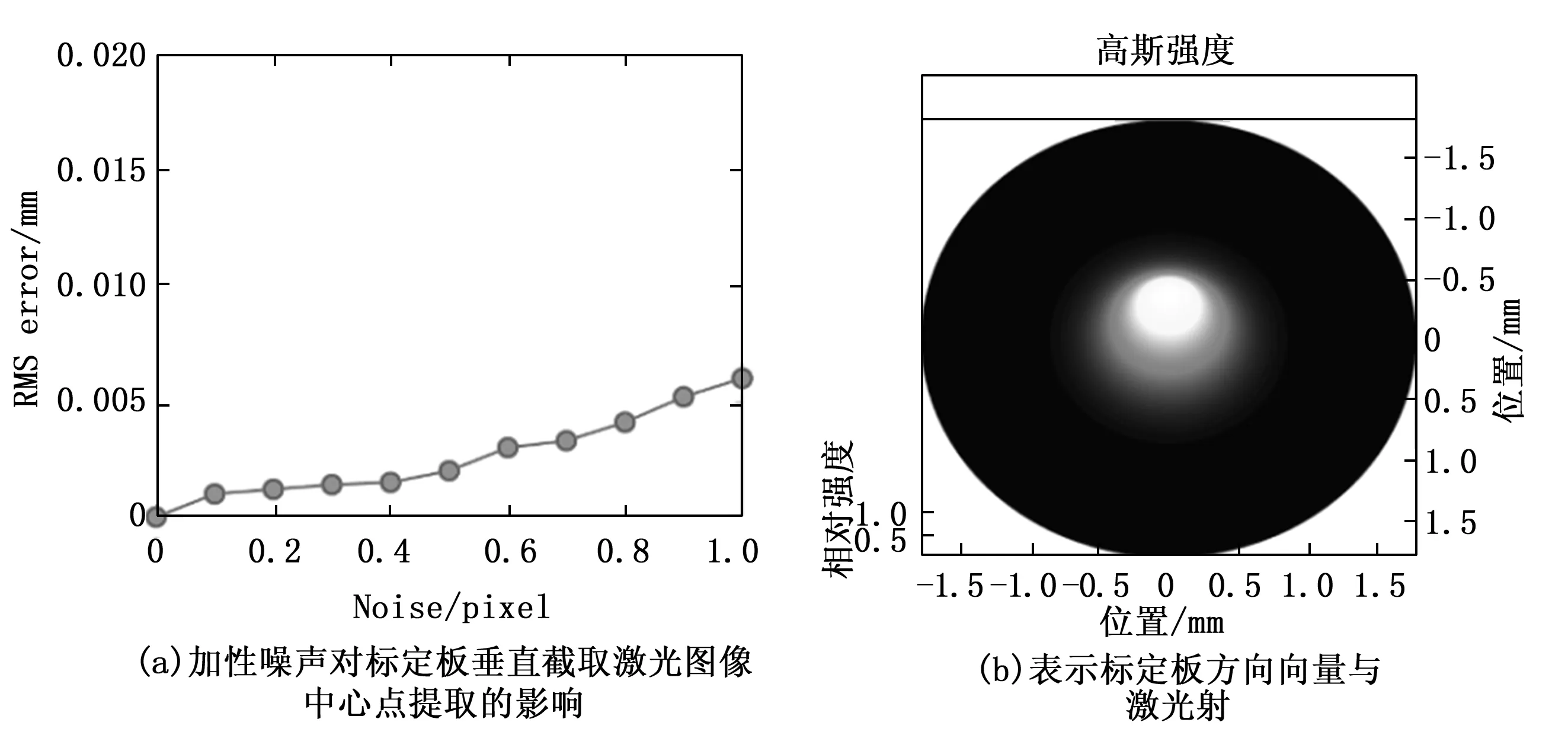
图5 激光散斑图像仿真及图像噪声影响对中心提取的影响
3.1.2 两相机之间距离因素
实验结果如图6所示,标定的外参的RMS误差随着相机之间距离的增加而增长,当其相对精度均小于0.3%,所提方法可应用于相机组的外参标定。
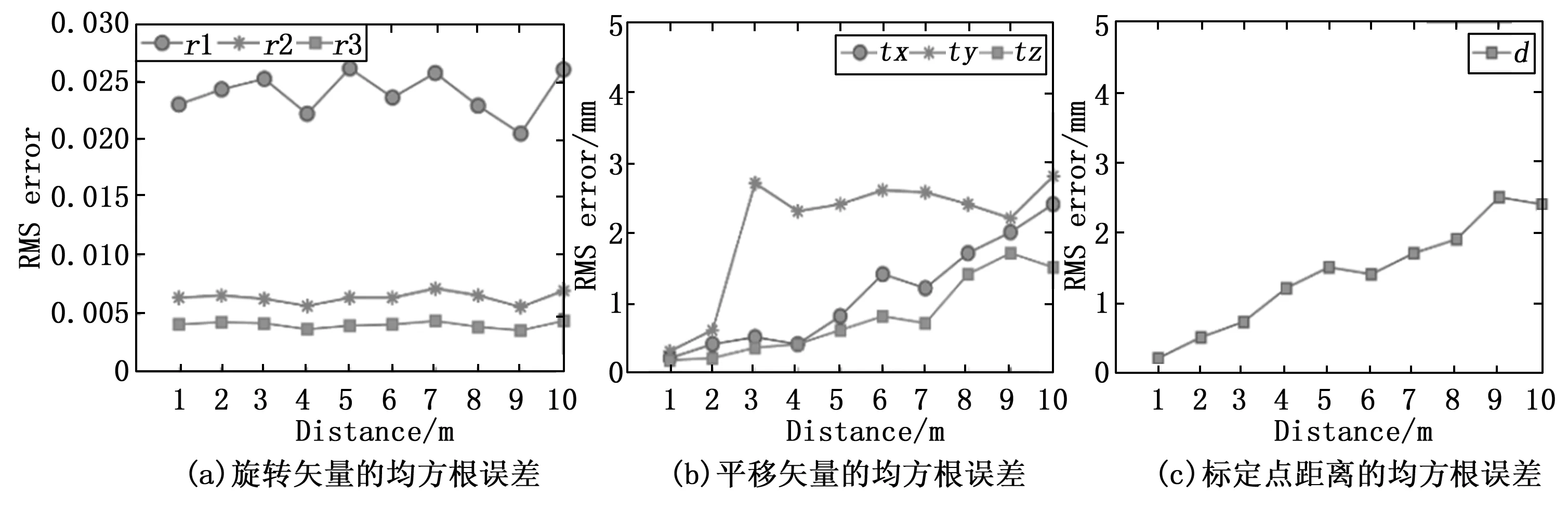
图6 相机之间距离对标定外参的RMS误差的影响
3.1.3 点激光器位置数量对精度的影响
实验结果表明,随着点激光器布置数量的增加,相机外参数的标定误差较快地减少。在不少于5个位置放置激光器的条件下,标志点之间距离的均方根误差小于0.07 mm,基于半镜面平面靶标的全局标定方法在较少点激光器的条件下,可得到较好的精度。
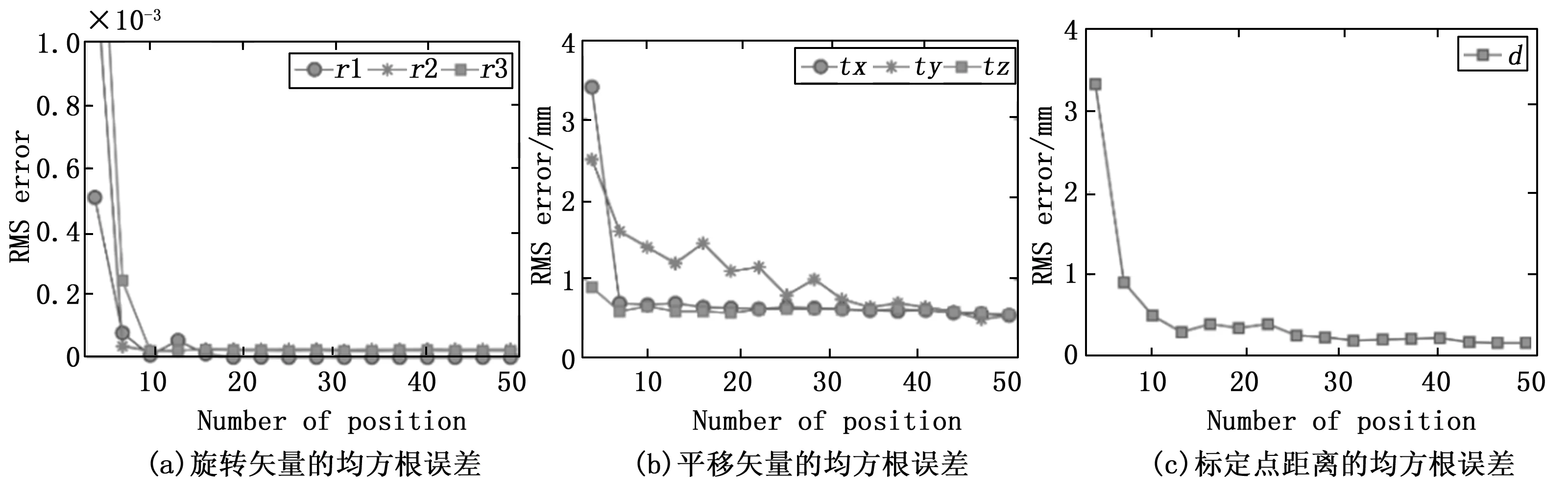
图7 点激光器的放值数量对标定误差的影响
3.2 实验过程
如图8所示,真实实验的环境采用了三相机组(相机1,2,3),其中相机1,2为维视公司的CMOS灰度工业相机,其图像分别率为2 048×1 536,像素尺寸为3.2×3.2 μm,相机采用的光学镜头为日本computar 28 mm镜头;相机3作为辅助相机,采用大恒公司CMOS工业相机,其图像分辨率为2 048×1 536,光学镜头为日本computar 18 mm镜头。相机组固定在三角支架上,激光器及标定板则固定在光学平台。

图8 三相机组对内参的标定
首先完成相机内参的标定工作,标定中采用的二维标定板以及半镜面标定板中的图案均为9×7个黑白相间的棋盘格,其间距为30 mm。在相机内参标定过程中,3个相机分别采集了20副二维标定板的图像,并采用张正友的方法完成内参的标定,标定结果如表2所示。
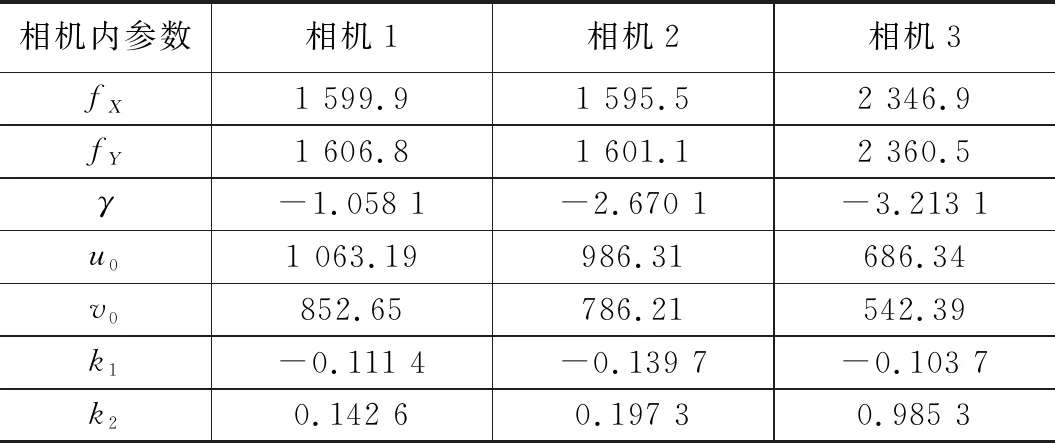
表2 内参的标定结果
完成相机组的内参标定后,为了验证外参的标定效果,设计了利用第三个相机作为关联视场,基于经典的张的标定方法完成没有公共视域的两相机(相机1,2)的外参标定,并与本文方法进行比较。其实验如下:
1)基于张正友的方法[33],分别完成相机1,3,相机2,3的外参的标定,从而在相机3的帮助下得到相机1,2之间的转换矩阵并做为真值与本文所提出的方法进行比较;
2)基于本文所提方法,分别在8个不同的位置布置点激光器,在相机1视场内放置半镜面标定板将激光射线反射到相机2的视场内;
3)分别在每个相机视场内用标定板截断激光射线,并采集6个散斑点图像,如图9展示了相应的散斑图像点。根据所提式(8)、(15)则可计算得到旋转矩阵,式(21)可计算得到平移向量。

图9 三相机组对外参的标定
表3给出了比较结果,假设张正友的方法为真值,则本文所提的方法最大误差为平移向量中的tx,在相机间距1.1 m的条件下,其误差为0.36 mm。

表3 全局标定方法和张正友方法的结果
4 结束语
针对无重叠视域的多相机全局标定问题,提出了基于半镜面平面靶标的标定方法。相比于现有的方法,所提出的方法具有更好的弹性、适应性,基本不受相机布局的影响,尤其适用于一维标定物无法贯穿两个相机的视场的情形,同时在相同标定精度及设备条件下,该算法计算更为简便,只需要计算一维标定物的散斑图像点的消隐点即可计算旋转矩阵,该算法具有广泛的应用前景。实验结果确认了所提出的基于半镜面平面靶标的外参标定方法具有较好的精度以及鲁棒性。

