基于滑模控制的导弹制导系统设计

王中浩，赵河明，路丰宁

(中北大学 机电工程学院，太原 030051)

0 引言

现代战争中，对武器精确打击目标能力的需求日益增强，导弹作为一种典型武器装备，在精确打击目标的场景中扮演着重要角色，导弹具有打击预定目标和自主控制飞行航迹的制导能力。导弹能实现制导功能的根本原因在于拥有制导系统，制导系统扮演着指挥官的角色，负责着生成决策与指令的重要职责。制导系统引导控制导弹的飞行航迹，沿预定航迹飞行，导向目标并实现摧毁目标。导弹导引头获取的外部信息的能力根本上决定了定位目标的准确性，其次，在信息准确的基础上，导引方法则对于导弹的路径跟踪能力有极大地影响效果。

传统导弹制导方案通常采用比例导航。比例导航原理简单，目前已能够实现在导弹制导系统中的成熟应用，但目前随着时代的发展进步，日益复杂的战场环境对导弹的制导技术提出了更高的需求。对于远程导弹，比例导航有诸多弊端，因为在进行远程打击任务时，目标在初始阶段有较大可能性无法被导弹探测到，往往需要在导弹行程的末尾阶段目标才能被识别到，因此需要在目标识别阶段之前采取不同的制导方法[1-5]。

随着智能控制理论研究的不断进展和现代控制理论在工程应用上的落实，制导系统在引导方式方面获得了更加多样化的选择，对于提高复杂环境下目标探测、识别、跟踪以及精确打击等功能提供了更多的可能性。目前，随着人工智能技术的不断发展，智能化的热潮席卷全球，武器的智能化目前得到越来越多国家的重视，世界各大军事强国都已开始着手智能导弹的研发。导弹的智能化是导弹未来的发展方向之一，而导弹制导系统的智能化是导弹智能化的基础。

目前，已有多种路径跟踪算法应用于制导律的研究中，如偏置比例导引律、最优制导律、向量场、神经网络智能制导律、模糊智能制导律、强化学习智能制导律等。但这些算法目前大多只在旋翼无人机(UAV)上实现，旋翼无人机一般被看作在二维横向运动的基础上增加垂直运动的系统，与导弹的运动特点有明显的差异，无法直接应用于导弹的制导系统，因此，基于先进的路径跟踪方法对导弹的制导系统进行改进是十分有必要性的工作[6-15]。

导弹的制导功能一般依靠航迹规划、制导策略和自动导航仪三部分实现，本文围绕上述三个部分对导弹的制导系统进行设计。首先，引入Dubins曲线对导弹的航迹规划进行优化，Dubins曲线能够创建更平滑的飞行轨迹，避免飞行物体的过冲运动与振荡现象[16-17]，可有效改善导弹的路径跟踪效果。然后，引入滑模控制对导弹的制导算法进行改进。滑膜控制是导弹制导算法中可实现的制导方法之一。该方法需要导弹实时的位置和方向角信息以及参考轨迹，计算导弹实现跟踪参考轨迹所需的参考方向角。滑模控制响应速度快、对系统内部参数变化及外部干扰不敏感、对非线性系统有良好的控制效果、适用于多输入多输出系统、实现方法简单[18-22]。

本文的结构如下：首先，确立了导弹的数学模型，包括运动学模型与动力学模型，并对该模型进行了讨论。然后，进行制导系统的设计，包括航迹规划、制导策略和自动驾驶仪的设计。最后，对设计的制导系统进行仿真模拟，观察制导系统在不同类型的参考路径下的表现，对仿真结果中的一些现象进行了解释，验证了该制导系统设计的可行性。

1 导弹的数学模型

导弹数学模型的建立，首先需要确立与导弹相关的坐标系。本文中使用到两个相关联的坐标系，分别是弹体坐标系(Xb-Yb-Zb)和地面坐标系(Xe-Ye-Ze)，都为右手坐标系。弹体坐标系用于描述导弹自身的位置和姿态，原点与导弹的重心重合，Xb轴与导弹轴线重合且正方向与前进方向一致，Zb轴指向下方。地面坐标系用于描述导弹相对于地面的位置和姿态，地球坐标系是固定的，并且以导弹发射位置点为原点。以上坐标系如图1所示，θ、Ψ、φ是弹体坐标系关于地面坐标系的欧拉角，θ是俯仰角，Ψ是偏航角，φ是滚转角，用于两个相关坐标系的坐标转换求解。导弹具有6个自由度(DOF)，3个平移自由度和3个旋转自由度。在弹体坐标系中，位置用向量(u,v,w)表示，旋转角用向量(p,q,r)表示，在地面坐标系中，位置用向量(ue,ve,we)表示，旋转角用向量(pe,qe,re)表示。

图1 弹体坐标系和地面坐标系

实际工作中，导弹的传感器接收到的位置信息基于地面坐标系，而旋转角信息基于弹体坐标系，需要将位置信息与旋转信息统一到同一个坐标系，因此需要确立地面坐标系与弹体坐标系的坐标转换公式。

平移运动的坐标转换表述为以下公式：

(1)

式中,θ是俯仰角，Ψ是偏航角，φ是滚转角，c是cos函数的简写，s是sin函数的简写。

旋转运动的坐标转换表述为以下公式：

(2)

本文研究的导弹模型采用侧滑转弯控制(skid to turn，STT)，使用一对“十”字舵面操纵俯仰和偏航运动，通过斜置尾翼来保持滚转角速度。

飞行过程中的导弹属于复杂的力学系统，大大增加了导弹动力学方程建立的复杂性，通过忽略次要因素，得到导弹的动力学模型，对此做出如下假设：

1)导弹视为刚体，不会产生气动弹性效应;

2)导弹视为质量集中在质心的质点;

3)导弹的滚动轴具有对称的气动效应。

基于上述假设的情况下，我们可以确立导弹动力学的基本方程，包括x,y,z三个方向上导弹质心的动力学方程与导弹绕质心转动的动力学方程。因此，导弹的动力学模型表述为以下方程组：

(3)

式中,T是导弹发动机推力，m是导弹质量，g是重力加速度，q是大气压，S是导弹表面积，d是导弹直径，CD,CS,CL是分别作用于x,y,z轴上的气动力系数，CR，CP，CY是分别作用于x,y,z轴上的气动力矩系数，IXX,IYY,IZZ是弹体坐标系各轴上的惯性力矩，上述空气动力系数之间具有如下的转换关系：

(4)

气动力系数是攻角α、侧滑角β、滚转舵偏角δa、俯仰舵偏角δe、偏航舵偏角δr、导弹马赫速度M、导弹旋转速度(p,q,r)的函数。α,β,M,q的值通过如下方程组进行计算：

(5)

2 导弹的制导系统设计

本章对设计的导弹制导系统进行介绍，包括轨迹规划、制导策略、自动驾驶仪三部分。

2.1 航迹规划

本文引入Dubins曲线进行轨迹规划。具体操作如下：

1)确定导弹必须到达的路径点位置(用三维向量(xi,yi,zi)进行表示)。

2)使用线段将各路径点顺次连接，生成分段折线。

3)引入Dubins曲线对折点进行优化处理。

引入Dubins曲线能够创建更平滑的参考轨迹，减少导弹运动中的振荡现象。本文中使用的Dubins曲线分为直线和圆弧两种轨迹，圆弧轨迹仅用于拐点，直线用于轨迹的其他部分。

Dubins曲线对折点优化处理需要在每个拐点上创建Dubins圆：首先在xy平面上初始化Dubins圆的位置，然后依次围绕x,y,z轴的旋转相应的角度α,β,γ。路径点i上的Dubins圆必须与路径点Wi-1,Wi,Wi+1形成的平面共面。Dubins圆的旋转矩阵如下：

(6)

为了验证生成Dubins曲线轨迹的可行性，进行以下试验：

预设一组导弹的路径点，如表1所示，导弹的航迹需依次经过表1所列的路径点，路径点间使用直线相连，并使用Dubins曲线对路径点附近的航迹进行圆滑处理，令Dubins圆半径为2 000 m。生成的Dubins曲线轨迹如图2所示，验证了生成Dubins曲线轨迹的可行性并将该曲线应用于后续的仿真部分，后续仿真章节将对Dubins曲线为航迹规划带来的改良效果进行分析。

表1 参考轨迹的路径点

图2 Dubins曲线轨迹

2.2 制导策略设计

路径规划工作完成后，需要设计制导策略来实现导弹对参考轨迹的跟踪。导弹制导由两个独立的制导系统组成，即偏航方向和俯仰方向的制导。偏航方向的制导需要实时的偏航角和位置坐标，俯仰方向的制导则需要俯仰角。上述的方向角和位置坐标信息，通过导弹上安装的定位系统与陀螺仪系统获得。

导弹制导系统接收到当前方向角与位置坐标信息后，结合预设参考路径，进行导弹方位角参考值的计算，从而实现对参考轨迹的跟踪，采用什么方法进行参考方位角的计算，决定了导弹对目标路径的跟踪效果。传统导弹制导系统的制导策略通常采用经典比例引导，本文引入滑模控制算法，对传统导弹的制导策略进行改进设计。

滑模控制系统是一种内部结构可以随时间变化的不连续系统，此种可以自主控制开关的控制特性使得系统在能够在一定情况下沿预定的状态轨迹作小幅度、高频率的调整运动，预定的状态轨迹被称作“滑动模态”，即所谓的“滑模面”。此种滑动模态是可以进行人为设计的，对滑动模态的设计决定了滑模控制的控制效果。滑动模态与系统参数无关，且不受外界干扰影响，因此处于滑模运动的系统具有很好的鲁棒性。

滑模控制方法是通过控制作用，使系统的实际路径运动到预定的滑模面内，根据滑模控制的理论，系统一旦进入设计好的滑模面内，在一定条件下系统对内部参数变动与外界干扰具有不变性。因此，滑模控制中的关键即保证系统顺利的进入滑模面内，此处控制其进入滑模面的方法基于平行接近原理，平行接近原理要求制导过程中视线角期望趋于零，实际情况中即导弹和目标之间视线角尽量可能的小。

制导系统在直线路径和圆弧路径需要采用不同的制导策略，Dubins曲线由直线段与圆弧段组成，因此需要预先对制导系统制导策略的转换逻辑进行设定，Dubins曲线中，于路径点处采用圆弧进行过渡，因此在切入路径点时，导弹需切换为圆弧制导，切出路径点时，需要切换为直线制导，以此类推，依次遍历所有路径点，最终到达目的地。具体判断逻辑如图3所示。

图3 制导策略转换逻辑

本文滑模控制的滑模面半径设置为导弹半径的两倍，导弹半径为0.28米，则滑模面半径为0.56米，导弹与参考轨迹的距离取导弹的质心坐标点进行计算，如图4(c)所示。只有导弹与参考路径的绝对距离大于0.28米时，才会触发制导系统。当导弹飞行在容许误差内时，制导系统暂停运行，导弹的自动驾驶仪不会接收到输入信号。

图4 算法图

偏航制导和俯仰制导有不同的制导策略，区别只在于计算的方向角与坐标平面不同，此处仅对偏航制导进行讨论。在直线路径和圆弧路径也有不同的制导策略，算法中所用到的变量如图4(a)、(b)所示，偏航制导在直线路径的算法见式(7)，在圆弧路径的算法见式(8):

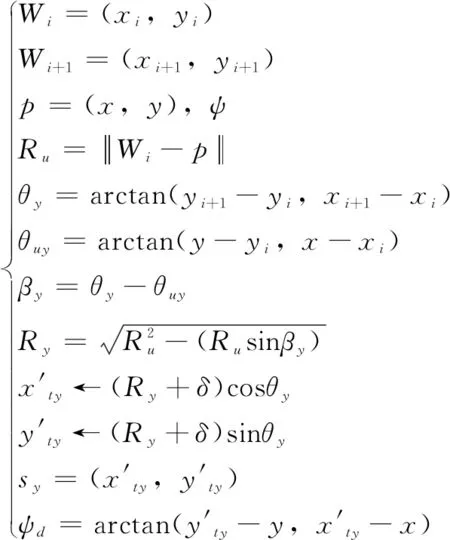
(7)

式中,Wi表示第i个路径点，Wi+1表示第i+1个路径点，p表示导弹在xy平面的坐标(x,y)和偏航角ψ，Ru表示路径点Wi与导弹的相对距离，θy表示θ在xy平面的分量，θuy表示θu在在xy平面的分量，βy表示β在在xy平面的分量，Ry表示Ru在在xy平面的分量，δ表示直线制导算法的调节参数，用于调节制导算法的响应强度，sy表示目标点在航迹上的位置，ψd表示ψ的参考值。

(8)

式中,O表示圆心，p表示导弹在xy平面的坐标(xi,yi)和偏航角ψ，d表示圆弧与导弹的正交距离，θy表示θ在xy平面的分量，λ表示圆弧制导算法的调节参数，用于调节制导算法的响应强度，ψd表示ψ的参考值。

计算出的偏航角和俯仰角的参考值，传递给自动驾驶仪部分，作为自动驾驶仪中的级联比例积分控制器的输入。

2.3 自动驾驶仪设计

自动驾驶仪负责接收制导策略计算出的偏航角和俯仰角目标值，作为级联比例积分控制器的输入，经过控制器的计算后得出舵翼的偏角值，传递给导弹弹翼的执行器，弹翼执行器根据控制信号进行相应动作，实现导弹的滚转、俯仰和偏航运动。

自动驾驶仪的核心控制器采用级联比例积分控制器，比例积分控制器是目前应用最为广泛的一种控制器，引入积分作用能消除余差，弥补了纯比例控制的缺陷，获得较好的控制质量。

导弹的滚动、俯仰和偏航都有各自独立且结构相同的自动驾驶仪，控制框图如图5所示。横滚、俯仰和偏航各自的自动驾驶仪区别仅在于输入和输出，输入分别为目标值Ψref、θref、φref，输出分别为舵偏角δa、δe、δr。

图5 自动驾驶仪方框图

3 仿真结果

对三种不同的参考轨迹进行了仿真模拟计算，分别是直线轨迹、圆弧轨迹和Dubins曲线。仿真中涉及的导弹参数如表2所示。

表2 模拟导弹参数

3.1 直线轨迹

模拟不同参数δ下制导系统对直线路径的跟踪表现。图6展示了导弹对直线路径的跟踪效果，图7展示了导弹与目标点之间误差距离的变化。表3展示了导弹实际飞行轨迹与参考轨迹的横向均方根误差(RMSE)与稳态误差，表4展示了导弹实际飞行轨迹与参考轨迹的纵向均方根误差(RMSE)与稳态误差。

图6 导弹对直线路径的跟踪效果

图7 导弹与目标点之间误差距离

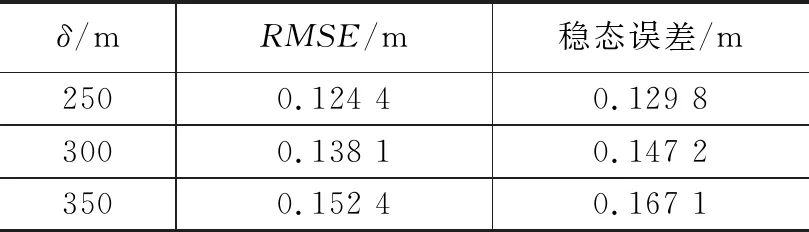
表3 横向均方根误差与稳态误差

表4 纵向均方根误差与稳态误差

由表3、表4可以看出，δ值减小，则导弹运动相对于参考轨迹的稳态误差也减小，但同时从图7可以看出，δ值的减小会导致实际航行轨迹产生更大的超调与振荡现象。发生这种现象的原因在于，减小δ值会使导弹试图更迅速地逼近参考轨迹，导致制导系统会传递给自动驾驶仪一个更大的参考角度，导致导弹飞行过程中更容易发生超调，但这有利于缩短导弹到达参考轨迹所需的时间。因为作用在纵向轴上的重力加速度，纵向比横向的均方根误差更大。

3.2 圆弧轨迹

模拟不同参数λ下制导系统对圆弧路径的跟踪表现。导弹的圆弧运动在竖直轴上不产生位移，所以只对偏航运动的制导进行仿真模拟。圆弧路径的夹角设置为180°，转弯半径为1 500米(导弹的最小转弯半径)。

图8展示了导弹对圆弧路径的跟踪效果，图9展示了导弹与目标点之间误差距离的变化。表5展示了导弹实际飞行轨迹与参考轨迹的均方根误差(RMSE)与稳态误差。

图8 导弹对圆弧路径的跟踪效果

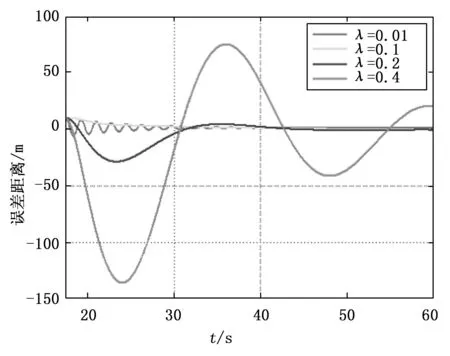
图9 导弹与目标点之间误差距离

表5 均方根误差与稳态误差

由表5可以看出，λ=0.1时，飞行轨迹的的稳态误差最小，从图9可以看出，λ=0.1时，飞行轨迹变化最平滑，超调与振荡现象最不明显。发生这种现象的原因在于，参考路径是圆弧形式，因此理论上存在一个最优参考角度，越接近理论上的最优参考角度，则实际飞行轨迹越迅速地逼近参考轨迹，同时变化也越平滑，可知λ=0.1时，舵偏角最接近理论上的最优参考角度。因此，以λ=0.1为基准，过大或过小都会导致飞行轨迹的稳态误差与振荡现象变大。

3.3 Dubins曲线轨迹

使用2.1生成的轨迹(如图2)进行仿真模拟。并对导弹在Dubins曲线轨迹和直线轨迹上的制导效果进行对比。

跟踪效果及对比如图10所示，导弹实际飞行轨迹与参考轨迹之间误差距离及对比如图11与图12所示。表6展示了导弹实际飞行轨迹与参考轨迹的均方根误差(RMSE)。

图10 采用Dubins曲线参考轨迹和4个路点滑动曲线制导仿真结果

图11 直线和Dubins曲线参考轨迹下导弹制导的横向误差

图12 直线和Dubins曲线参考轨迹下导弹制导的纵向误差

表6 不同参考轨迹下导弹与参考轨迹间的均方根误差

从仿真结果中可以看出，本文设计的导弹制导系统的路径跟踪能力表现良好，曲线平滑无明显突变，且横向误差与纵向误差都较小，对直线轨迹和Dubins曲线轨迹都都有出色的轨迹跟踪效果。

对不同的参考轨迹进行跟踪时，导弹的跟踪效果有明显差异。对Dubins曲线轨迹进行跟踪时，实际飞行轨迹与参考轨迹间的均方根误差较小。在拐点处，对Dubins曲线的跟踪效果显著优于对直线的跟踪效果，出现这种现象的原因是Dubins曲线轨迹在拐点处的过渡更平滑，相应地减小了导弹在拐点处的运动超调。

改进前后的路径仿真如图13所示，以Dubins曲线为参考路径，改进前后与参考轨迹之间的误差距离及对比如图14、图15所示。表7展示了导弹实际飞行轨迹与参考轨迹的均方根误差(RMSE)。

图13 改进前后飞行轨迹的仿真结果

图14 改进前后与参考轨迹的横向误差

图15 改进前后与参考轨迹的纵向误差

表7 改进前后与参考轨迹间的均方根误差

从仿真结果中可以看出，本文改进后的导弹制导系统对参考轨迹的跟踪能力更强，横向误差与纵向误差都较小，且收敛速率明显快于基于经典比例导引法的传统制导系统。基于经典比例导引法的传统制导系统产生的弹体抖动较为强烈，尤其在拐点处，发生了明显的超调，而本文设计的经过改良后的制导系统显著地抑制了导弹的运动超调与振荡现象。

4 结束语

本文设计了一种基于滑模控制的新型导弹制导方法，引入Dubins曲线进行路径规划，并引入滑模控制进行制导策略的设计。最后，对设计的制导系统进行不同类型参考轨迹下仿真模拟。

对比不同类型的参考轨迹下系统的表现，对比不同轨迹下与参考轨迹间的均方根误差，并观察误差随时间的变化，证明了Dubins曲线能有效改善导弹的路径跟踪能力，减少超调与振荡现象。

此外，为了进一步体现本文设计的制导系统相对传统制导系统的改良效果，对以经典广义比例导引作为制导律的制导系统进行仿真，结果与本文设计的经过改良后的的制导系统表现进行对比，证明了改进后的制导系统性能的优越性，收敛速度有明显提高，能够有效抑制导弹飞行中的振荡现象，证明了本研究所做的改进工作是可行的。

后续研究应引入其他不同的制导策略，并寻找复杂度更高、更能验证制导系统的路径跟踪性能的路径作为参考轨迹进行仿真。