基于微分几何反馈线性化的高超声速飞行器控制系统实现

杨 凡，黄 颖，陈云松，曾 皓

(1.中国科学院 成都计算机应用研究所，成都 610041 ； 2.四川省自主可控电子信息产业有限责任公司，成都 610041)

0 引言

“反馈线性化”是一种通过微分几何处理或者动态反馈补偿的方式，将非线性数据参量转换成线性排列形式的处理方法。在“反馈线性化”的认知理论中，微分几何处理是一种最为常见的执行方式。微分几何反馈线性化处理能够在在相邻数据信息节点之间，建立一种单向映射关系，随着数据信息传输量的增大，节点与节点之间的连接关系逐渐趋于密集，此时各类抽象数学问题都能得到较好解决[1]。在实际应用过程中，微分几何反馈线性化方程的建立条件较为苛刻，不但对输入函数集合的映射能力提出了要求，还规定集合内所有存储数据信息之间都不能具有逆运算关系。一般来说，满足反馈线性化要求的数据信息都具有明显的解耦性特征，且随着微分几何方程的建立，数学方程的表达能力也会不断增强，此时根据数值解所处的区间范围，就可以知道当前运算公式是否满足实际应用需求[2]。

高超声速飞行器具有突防成功率高、运动稳定性强等特点，其飞行速度近似等于普通音速飞行器的五倍，有着极强的潜在经济价值。其动力系统由喷气式发动机、超燃冲压发动机、热防护结构等多个元件共同组成。随着飞行器行进距离的延长，发动机设备的动力输出能力也会不断增强，此时电动机元件的做功量快速增大，极易造成横滚角、纵滚角数值的持续增大，并最终影响飞行器元件的稳定运动能力[3]。为避免上述情况的发生，基于非仿射模型的控制系统选取STM32F103CB芯片作为核心控制器结构，利用ADXL345加速度计、L3G4200陀螺仪两个应用元件，对飞行器设备的实时运动能力进行统计，再联合HC-SR04超声波传感器度量电动机元件的做功情况[4]。然而此系统的实际应用能力有限，并不能将横滚角度数值、纵滚角度数值与理想角度数值之间的物理差值控制在既定水平标准之内，并不能使飞行器元件呈现出绝对平稳的运动状态。

为解决上述问题，设计基于微分几何反馈线性化的高超声速飞行器控制系统，并针对其实用性能力展开研究。

1 高超声速飞行器概述

高超声速飞行器是一种以5倍音速以上飞行的飞机、导弹、炮弹等飞行器，它的突防成功率很高，具有很大的军事和经济价值。由于高超声速飞行器的飞行特性，其飞行包络线的宽广，难以用一个单独的工作环境来描述，而其气动和气热性能又受飞行器的任务限制和设计要求的限制。高超声速飞行器的工作环境更为复杂。飞行器在高超音速飞行过程中，存在着动压效应、粘性效应、强/弱真实气体效应、低密度效应、机体表面辐射效应等诸多因素。高超声速飞行器的飞行环境瞬息万变，其飞行环境的特殊性和复杂性，使其在大气、热场等方面发生了较大的变化。

飞行器在高超声速飞行过程中，其末端的空气马赫数是相当大的。当气流穿过环绕飞机机身的冲击波时，气流速度会变得缓慢，并且在冲击层中会有较高的温度。此时，粒子的动能转换成了热能，在飞行器的四周产生了一种吸热作用，周围的空气也开始了分解和电离。与此相适应的是，高超声速飞行器的机械结构有两种：绝热压缩和粘滞能量分布。由激波层的热空气向机体表面传递的速度受多种因素的影响，如：远端气流速度、气流方向、飞行器整体结构、表面温度、气流温度与飞行器表面温差等。

在马赫数为6.8的情况下，在35公里的高空进行轨道分离。在该阶段，由于大气动力干扰影响较大，因此在分离阶段要充分考虑其安全性。首先要确保飞行器与入轨飞行器之间的分离速度要快，并且要有足够的间隔；然后再建立一个高效的控制体系，以确保两个一体化的系统在分离时得到最优的控制；另外，在飞行器发生紧急情况时，应采取相应的性能补偿措施，尽量减少飞行器的飞行事故；最后是运载工具和入轨飞行器之间不再有交互作用，只有它们自己的轨道。

2 高超声速飞行器控制系统主体结构设计

高超声速飞行器控制系统的主体应用结构由电源管理模块电路、电机驱动器、螺旋桨、IMU惯性传感器模块、GPS定位模块及PID控制器六部分共同组成，本章节将针对上述设计元件展开深入研究。

2.1 电源管理模块电路

高超声速飞行器电源管理模块电路由5 V 转 3.3 V、12 V转 5 V两个稳压分路结构组成(详细连接结构如图1所示)。PUI连接端输入的高压交流电可以在LM2596元件的作用下，转换成12 V的输出形式，以供飞行器电动机元件的直接使用。LM1117设备所能承载的电压水平相对较低，一般来说，在R1、R2、R3电阻接入阻值不发生改变的情况下，该结构元件可以将12 V的输入电压转换成3.3 V的输出形式，且在整个转换过程中，LM2596元件两端的物理电压始终维持在5 V左右[5-6]。下级PUI连接输入端管控C1电容、C2电容与电量延迟设备，可以在IN4007反相器元件的作用下，形成一个完整的电量闭环回路，且该回路体系存在于电源管理模块电路下端。分属于电源管理模块电路不同分路中的连接电阻的接入阻值水平也有所不同，一般遵循负载电压数值越大，接入电阻阻值水平也越大的原则。

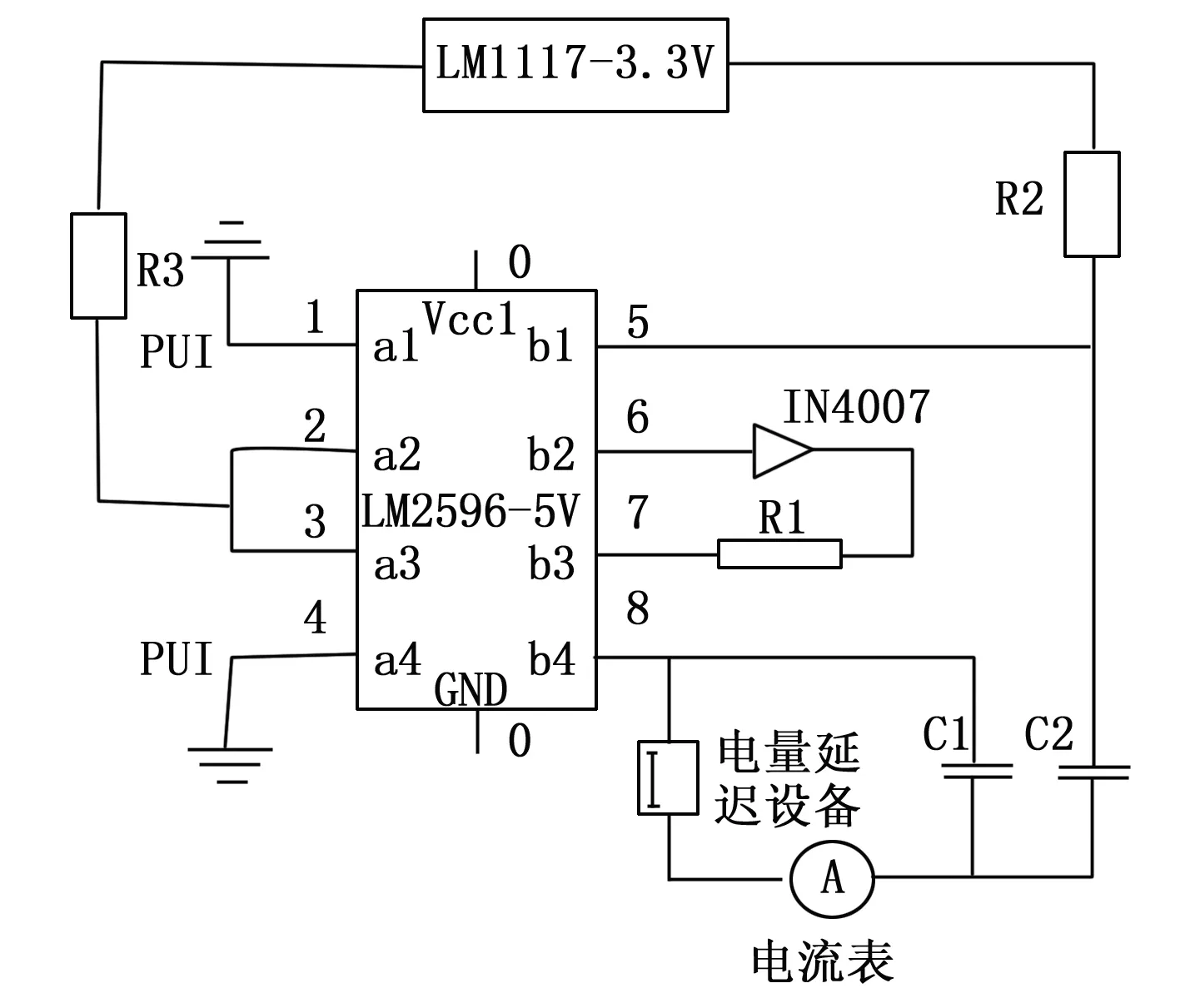
图1 电源管理模块电路结构示意图

电流表元件负责检测电量延迟设备中传输电流的具体数值，当C1电容设备、C2电容设备的连接能力发生改变时，电量延迟装置的连接现状也会随之出现变化，此时控制系统主机就可以根据电流表内显示数值的变化情况，来判断高超声速飞行器元件的实时运动状态。

2.2 电机驱动器

由于高超声速飞行器均采用无刷电机驱动的运作形式，所以为使电源管理模块电路中所有电量信号都能保持相对稳定的输出状态，在设计控制系统硬件执行单元时，必须选取一个额定工作能力较强的电机驱动器设备，来处理未能被传感器主机完全消耗的电量传输信号[7-8]。在选取电机驱动器元件时，需同时参考额定电压、额定电流、阻电容数值等多方面内容。由于高超声速飞行器的运动速率较快，所以电源管理模块电路中的电信号输出量始终较大，对于电机驱动器元件而言，为了稳定承载所以电量信号，其额定电压数值必须大于220 V。在电机内阻数值不发生改变的情况下，负载电压数值越大，驱动器元件内传输电流的数值水平也就越高[9]。完整的高超声速飞行器电机驱动器选型原理如表1所示。

表1 电机驱动器选型原理

电机驱动器作为一个从属负载元件，其各级电量指标的数值水平会随着电源管理模块电路中电信号输出量的改变而不断变化。

2.3 螺旋桨

螺旋桨作为高超声速飞行器的主体行进装置，具有较强的旋转运动能力，且随着螺旋桨转速的改变，高超声速飞行器元件的运动行进速度也会发生变化[10-11]。图2反映了高超声速飞行器螺旋桨的主要俯视结构与侧视结构。

图2 高超声速飞行器螺旋桨的主要结构元件

各级元件结构的具体应用能力如下：

1)主旋翼：螺旋桨运动元件的主要组成部分，包含于电量接线内部，随着电信号输入量的改变，主旋翼结构的转动速度也会发生变化[12]。且该结构具有较强的主动作用能力，其转速水平可以直接影响下级从动旋翼元件。

2)从动旋翼：作为主旋翼元件的下级附属结构，从动旋翼的物理面积相对较小，在高超声速飞行器的运动过程中，该元件并不能直接与电量传输信号相接处，因此其对于传输电流的感应敏感性相对较弱。

3)电量接线：环绕于主旋翼结构外部，是高超声速飞行器电量信号的唯一传输通路。

4)电动机接口：高超声速飞行器电机驱动器与螺旋桨结构的连接端口。

5)振片：具有振动能力的电量感应装置，会随着高超声速飞行器电信号输入量的改变，而呈现出不同频率的振动状态。

6)电感装置：电机驱动器元件的负载接入位置，能够准确感知高超声速飞行器电量信号的数量级水平。

2.4 IMU惯性传感器模块

惯性传感器模块负载于电源管理模块电路下端，与电机驱动器元件具有同等级的调试能力，能够影响高超声速飞行器设备的实际运动能力，并可以在IMU控制芯片的作用下，更改飞行器加速度、角速度等指标参量的数值水平[13]。IMU控制芯片存在于惯性传感器模块内部，上、下、左、右分设GND输入、NCC输出、VDD连接、VCC连接4个端口组织。其中，GND输入端管控r1接线与r2接线，负责将惯性传感器模块与电机驱动器元件相连。NCC输出端管控r3接线与r4接线，负责将惯性传感器模块与电源管理模块电路相连，在高超声速飞行器保持运动状态的情况下[14]。VDD连接端口管控D1、D2、D3、D4负载节点，负责将电量传输信号导入至惯性传感器模块内部。VCC连接端口管控C1、C2、C3、C4负载节点，负责将惯性传感器模块内部的剩余电量传输信号转送给下级连接元件。IMU惯性传感器模块连接结构如图3所示。

图3 IMU惯性传感器模块连接结构

在高超声速飞行器控制系统中，IMU惯性传感器模块起到承上启下的连接作用，可以同时调节电机驱动器、PID控制器等多个元件结构之内的电量信号负载关系。

2.5 GPS定位模块

GPS定位模块作为控制执行指令的核心生成元件，由GPS定位组件、NMEA定位芯片两部分共同组成，可在统计高超声速飞行器行进节点所处位置的同时，建立与运动位移轨迹相关的数学表达式。对于高超声速飞行器控制系统而言，GPS定位模块所定义的位移轨迹表达式必须满足微分几何反馈线性化约束原则[15-16]。为使高超声速飞行器控制指令得到稳定传输，GPS定位组件接受NMEA定位芯片的直接控制。当飞行器运动轨迹趋于完善时，控制主机开始同步转存状态，此时IMU惯性传感器模块会促进剩余电量信号的快速传输，直至这些数据信息参量能够被GPS定位组件完整记录。图4反映了GPS定位模块中的控制指令传输原理。

图4 GPS定位模块中的控制指令传输原理

为避免高超声速飞行器出现不可控运动现象，GPS定位模块的连接行为接受电机驱动器元件与IMU惯性传感器模块的同时调节。

2.6 PID控制器

PID控制器能够根据高超声速飞行器的滚转角数值，平衡IMU惯性传感器模块与GPS定位模块之间的连接关系，从而使得电源管理模块电路中的电量信号输出行为能够保持绝对稳定的存在状态[17]。在微分几何反馈线性化原理的作用下，高超声速飞行器在每一个俯飞行为后期都会保持较长时间的快速前行状态，此时为使油门量能够恢复至原始位置处，PID控制器会根据飞行器机体的倾斜角度，来协调控制指令的输出强度，从而使得螺旋桨元件呈现出较为稳定的运动形式[18]。在实际应用过程中，PID控制器同时以高超声速飞行器的横滚角度数值、纵滚角度数值作为输入变量，在微分几何反馈线性化原理的认知中，这些变量指标间存在明显的可抵消关系，这也是高超声速飞行器控制系统能够保持长期稳定运行状态的主要原因。

3 基于微分几何反馈线性化的飞行器控制程序

3.1 飞行器运动轨迹的微分处理

(1)

(2)

作为微分几何反馈线性化原理的表达基础，微分处理方程的取值结果不宜过大。

3.2 控制向量反馈系数

控制向量反馈系数决定了主机元件对于高超声速飞行器元件的实时控制能力[21]。在已知飞行器运动轨迹微分处理表达式的前提下，该项指标参量的物理取值越大，就表示主机元件对于高超声速飞行器元件的实控能力越强，此时飞行器设备呈现出的线性化运动行为也就越明显；若反馈系数指标的物理取值相对较小，则表示主机元件对于高超声速飞行器元件的实控能力相对较弱，此时飞行器设备呈现出的线性化运动行为也就较为模糊[22]。设φ表示高超声速飞行器的运动反馈向量，s表示飞行器运动航迹标记系数初始值，k表示运动航迹标记系数的最大取值结果，ds表示与系数s相关的高超声速飞行器运动行为控制向量，dk表示与系数k相关的高超声速飞行器运动行为控制向量，γ表示反馈调制参量。在上述物理量的支持下，联立式(2)，可将基于微分几何反馈线性化原理的高超声速飞行器控制向量反馈系数表达式定义为：

(3)

在判别高超声速飞行器运动行为能力时，相关参量指标的取值，必须遵循微分几何反馈线性化处理原则。

3.3 几何信号解析

几何信号解析是设计高超声速飞行器控制系统的必要执行环节，能够按照既定表达式条件，对控制波动信号的传输行为进行按需调试，从而在保证飞行器设备满足既定运动控制需求的同时，完成对线性化曲线向量的调节与规划[23-24]。规定η表示高超声速飞行器控制信号的线性化解析强度，μ1、μ2表示两个随机选取的高超声速飞行器控制信号微分反馈定标值特征参量，且μ1≠μ2的不等式条件恒成立，f表示既定的微分控制信息解析处理权限值。联立上述物理量，可将高超声速飞行器控制系统的几何信号解析表达式定义为：

(4)

在高超声速飞行器控制系统中，为了不违背微分几何反馈线性化处理原则，μ1、μ2指标的选取都不能等于物理自然数“1”。

3.4 线性化姿态解算

线性化姿态解算表达式能够帮助控制主机确定高超声速飞行器元件滚转角的数值变化情况，作为一项矢量参考指标，解算表达式的定义结果具有数值、方向两项参考约束条件，其中数值决定了线性化姿态表达式的解算强度，而方向则决定了系统控制指令的实时传输行为[25-26]。规定c表示飞行器运动线性路径解算系数的初始值，lc表示飞行器运动姿态的初始定标值，tc表示飞行器运动控制特征的初始值，hc表示微分几何运动曲线反馈系数的初始值。在上述物理量的支持下，联立式(4)，可将控制系统对于高超声速飞行器的线性化姿态解算表达式定义为：

(5)

式中，ϖ表示飞行器滚转角定标值，ξ表示同步控制系数。对于高超声速飞行器控制系统而言，线性化姿态解算表达式决定了微分几何反馈线性化算法的实际应用能力，故而在制定控制执行指令时，必须将该项表达式的计算结果控制在既定数值标准之内。

4 实验分析

为了验证设计的基于微分几何反馈线性化的高超声速飞行器控制系统的有效性。在Matlab仿真平台中开展实验分析。横向滚角数值、纵向滚角数值均可以用来描述高超声速飞行器元件的运动稳定性。通常情况下，若横滚角度数值、纵滚角度数值与理想角度数值之间的差值水平较小，则表示当前情况下高超声速飞行器元件的运动稳定性相对较强；反之，若横滚角度数值、纵滚角度数值与理想角度数值之间的差值水平较大，则表示当前情况下高超声速飞行器元件的运动稳定性相对较弱。

本次实验选取基于微分几何反馈线性化的高超声速飞行器控制系统作为实验组应用方法，选取基于非仿射模型的控制系统作为对照组应用方法。分别利用实验组、对照组应用系统对实验用高超声速飞行器元件进行控制，并记录所得变量指标的具体数值变化情况。

表2记录了所选取飞行器设备型号及相关实验参数的配置结果。

表2 实验参数设置

表3给定了高超声速飞行器元件横滚角度、纵滚角度的理想数值。

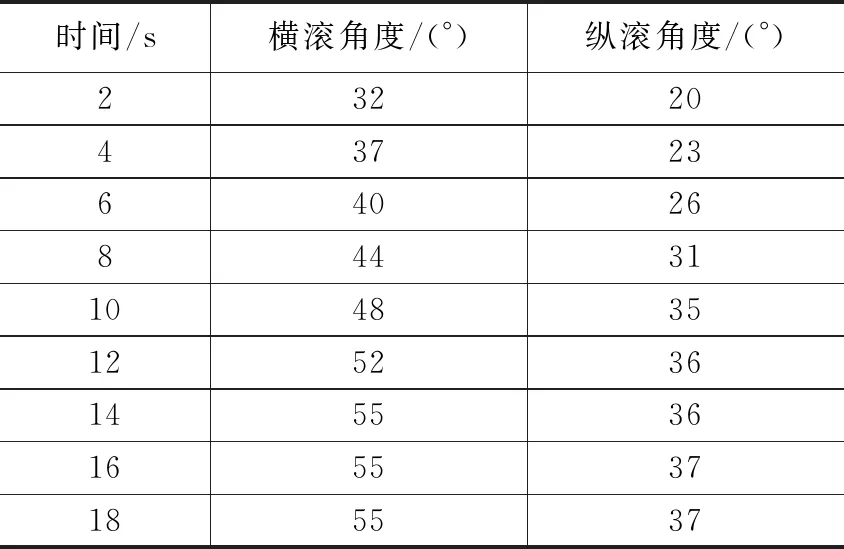
表3 方向性滚角的理想数值

分析表3可知，高超声速飞行器元件的横滚角度均值水平相对较高，而纵滚角度均值水平相对较低。在2～14 s的实验时间内，高超声速飞行器元件横滚角度数值呈现出连续增大的变化趋势；在14～18 s的实验时间内，高超声速飞行器元件横滚角度数值则始终保持稳定存在状态。在2～10 s的实验时间内，高超声速飞行器元件纵滚角度数值呈现出大幅上升的变化状态；在12～18 s的实验时间内，高超声速飞行器元件纵滚角度数值继续保持不断增大的变化状态，但其单位上升幅度相对较小。

图5反映了实验组、对照组横滚角度及其与理想角度数值之间的差值对比情况。

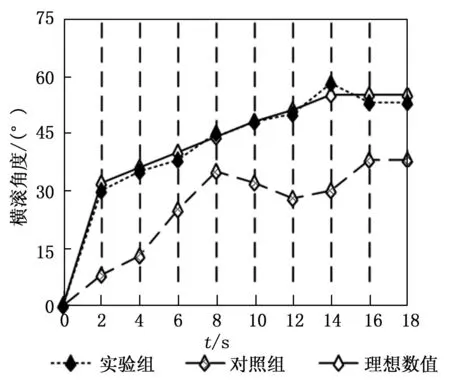
图5 高超声速飞行器的横滚角度

分析图5可知，当实验时间处于0～8 s、12～16 s之间时，对照组横滚角度均呈现出连续上升的数值变化状态，其最大值达到了38°，与理想极大值55°相比，下降了17°；当实验时间等于8 s时，对照组横滚角度数值与理想角度数值之间的差值最小，为9°。整个实验过程中，实验组横滚角度的数值变化趋势基本与理想数值保持一致，当实验时间等于14 s时，实验组横滚角度数值与理想角度数值之间的差值最大，为3°，其差值水平远小于对照组。

图6反映了实验组、对照组纵滚角度及其与理想角度数值之间的差值对比情况。

图6 高超声速飞行器的纵滚角度

分析图6可知，当实验时间等于4 s时，对照组高超声速飞行器纵滚角度的物理数值最大，达到了58°，与理想极大值37°相比，差值为18°；当实验时间等于12 s时，对照组高超声速飞行器纵滚角度数值与理想角度数值之间的差值最小，为11°。整个实验过程中，实验组纵滚角度的数值变化趋势也基本与理想数值保持一致，当实验时间等于6 s时，实验组纵滚角度数值与理想角度数值之间的差值最大，为4°，其差值水平远小于对照组。

综上可知，本次实验的结论如下：

1)基于非仿射模型的控制系统对于高超声速飞行器方向性滚角数值的控制能力较弱，在促进飞行器元件保持平稳运动方面的实际应用能力也就相对较弱；

2)基于微分几何反馈线性化的控制系统对于高超声速飞行器方向性滚角数值的控制能力较强，能够将横滚角度数值、纵滚角度数值与理想角度数值之间的差值控制在较低数值水平，符合维持飞行器元件保持平稳运动状态的实际应用需求。

5 结束语

在微分几何反馈线性化算法的作用下，高超声速飞行器控制系统重新规划了电源管理模块电路、电机驱动器、IMU惯性传感器模块、GPS定位模块等多个硬件执行结构的实时连接状态，又根据微分处理原则，计算控制向量反馈指标的具体数值，从而实现对飞行器元件线性化运动姿态的实时解算。与基于非仿射模型的控制系统相比，随着基于微分几何反馈线性化的控制系统的应用，横滚角度数值、纵滚角度数值均不会与理想角度数值产生较大的物理偏差，这在维持高超声速飞行器元件的平稳运动状态方面确实具有较强的实用性意义。