基于改进型LS-SVM技术的煤泥浮选智能优化控制方法
郭 伟,贾永飞,赵 欣
(中煤华晋集团有限公司 王家岭选煤厂,山西 运城 043300)
0 引言
目前,我国煤炭资源禀赋条件差,高含杂低品质煤资源储量丰富,随着优质煤炭资源的逐渐消耗与国家“双碳”战略的实施,低品质煤大规模分选提质已成为保障国家能源安全和煤炭行业高质量绿色发展的战略选择。煤泥浮选是一个多变量、大时滞的复杂非线性过程,在选煤中浮选用于分离出形成灰分的矿物质和粒度小于0.5 mm的细煤中的含碳物质。其中,洁净煤灰含量是浮选产品质量的重要指标,当煤在一定时间内(即相对稳定的进料)保持一致时,洁净煤的灰分含量主要受操作条件的影响[1]。单一静态估计模型通常会获得令人满意的结果。然而,由于过程中的各种干扰、原材料的异质性和工作条件的波动等因素,单一静态估计模型的精度可能会随着时间的推移而降低[2-3]。
为了表示浮选产品指数,国内外相关学者提出了许多基于浮选动力学的数学模型。其中国内文献[4]公开了一种人工神经网络(ANN, artificial neural network)算法模型,将线性模型和非线性补偿相结合,通过概率密度估计选择最佳参数。但该算法公式通常很复杂,包含许多可变参数,在浮选工艺的实际实施中,每小时对洁净煤进行采样和灰分分析,导致工人劳动强度高。文献[5]提出了基于最大相关性和最小冗余(MRMR,max-relevance and min-redundancy)和半监督高斯混合模型(SSGMM, semi supervised Gaussian mixture model)联合分类模型的优化方法,评估煤泥浮选的药剂剂量、泡沫深度和回收率值。但由于时间延迟太长,从分析中获得的灰分含量无法及时指导浮选过程的实际操作,浮选过程的操纵变量不能及时调整,影响产品的质量和稳定性。此外,文献[6]公开一种低品质煤泥浮选过程强化研究进展及其思考,该技术通过将煤炭作为当前最主要的碳排放源,能够实现碳达峰、碳中等综合信息分析。但该方法浮选低品质煤泥精度低,无法满足实际应用的要求。
1 煤泥浮选过程设计
面对上述背景下煤炭浮选方法存在的问题,该研究设计了一种旋流微泡浮选柱(简称FCMC),该装置能够在煤泥尾矿库中合理筛选出符合要求的含碳物质,具体装置如图1所示。
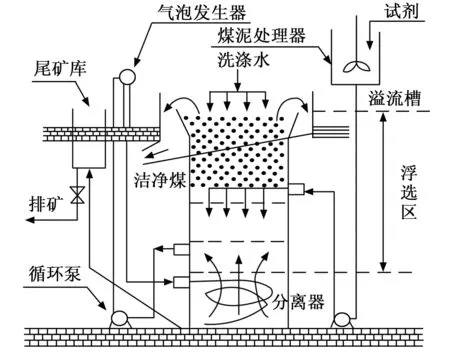
图1 FCMC浮选柱示意图
从图1中可以看出,FCMC浮选柱大体上分为3个工作区:泡沫区、收集区和清除区,FCMC浮选柱洗涤装置和溢流槽位于塔的顶部,入口的位置约为立柱高度的三分之一。煤泥浮选过程中精煤矿从溢流槽排出,尾矿从底流口排出。循环泵与气泡发生器相连,位于塔体外部;当循环泵喷射煤浆时,气泡发生器吸入空气,并将空气与煤浆中的起泡剂混合;然后,在减压过程中释放出大量微气泡。微气泡沿切线方向进入色谱柱,并在离心力作用下旋转移动。气泡和矿化气固骨料通过旋转流中心向上移动,进入收集区。未矿化尾矿向下移动,通过底流排出,进料和气泡的反向运动促进了矿化和气固骨料的形成。
图1中,FCMC浮选柱的分离过程受到各种影响因素的影响,如柱高、粒度分布、进料灰分含量、浓度、流速、空气流速、洗涤水流速、试剂用量和泡沫深度(矿浆水平)[7-8]。当进料性能稳定时,洁净煤灰含量主要受多种工作条件的影响,如表1[9]所示。
如表1可以看出,煤泥浮选是一个复杂的三相过程,涉及到气体、液体和固体[10]。通过参考多种文献与实验分析表明,影响浮选产品质量的因素很多,各因素之间存在耦合,浮选精煤灰分的在线测量比较困难,但可以采用软测量技术与算法模型解决这一问题[11]。目前对洁净煤灰分评估模型的研究主要集中在单一模型的建立上,不能完全适应工况的波动和煤种的多样性[12]。为此,本研究提出了一种基于模型更新和多最小二乘支持向量机的浮选精煤灰分综合评估模型。该方法有效地提高了浮选过程的智能控制水平,实现了浮选过程的闭环优化控制,下文阐述了建立过程。

表1 洁净煤灰含量影响条件
2 煤泥浮选智能优化评估模型的建立
本研究设计的综合评估模型大致分为3个部分:首先,建立了基于LS-SVM(least squares-support vector machine)的单一煤种的单一估计模型,并利用引力搜索算法(GSA,gravitational search algorithm)对其内部参数进行了优化;其次,设计了模型更新策略,解决了单一模型精度下降的问题;此外,为了解决模型失配问题,还研究了由多个单一模型组成的多个LS-SVMs模型以及模型切换机制,下文将分别展开论述。
2.1 基于LS-SVM的单一评估模型
在实际浮选生产中,当进料相对稳定时,净煤灰含量主要受操作条件的影响。因此,首先建立了单级原煤的洁净煤灰含量评估模型。在LS-SVM中,用等式约束代替SVM的不等式约束,因此,算法的复杂度降低,计算速度大大加快,能够满足工业过程的实际要求[13]。
对于LS-SVM模型的构建过程,首先假设煤泥数据集合S={(x1,y1)…(xi,yi)},其中i=1,2…N,N表示煤泥样本数,xi和yi分别是指输入煤泥浮选参数向量与之相应的输出煤泥浮选参数向量,通过非线性映射函数将输入煤泥数据映射到高维特征空间[14]φ(·),建立了回归模型g(x)如式(1)所示[15]:
g(x)=wT×φ(x)+b
(1)
式(1)中,wT表示权重向量,b表示偏差。根据目标模型结构风险最小化原则,回归问题可以转化为约束二次优化问题,如式(2)所示:

(2)
式(2)中,γ是正则化参数,ei是松弛系数。为了解决上述优化问题,该研究引入拉格朗日乘子来获得目标函数,如式(3)所示:
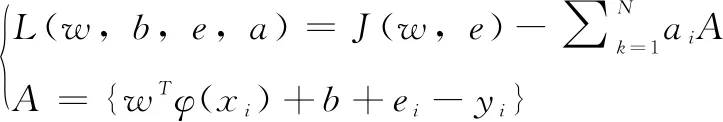
(3)
根据最优系统理论[16]中的Karush-Kuhn-Tucker(KKT)条件,可以得到以下线性方程,如式(4)所示:
(4)
式(4)中,Ω=K(x,xi) =φ(x)Tφ(xi),K(x,xi)表示满足Mercer定理条件的核函数。最后,回归函数f可以表示为:
(5)
通过以上算法过程构建LS-SVM模型。
2.2 数据预处理与模型参数优化
为了提高LS-SVM模型的收敛速度和精度,需要对所有煤泥样本数据进行归一化处理。本研究采用最小最大法,其表达式为:
(6)
煤泥浮选问题是一个复杂的计算过程,影响洁净煤质量的变量很多,为了去除冗余信息,降低LS-SVM的计算复杂度,同时保留最大的数据信息,采用主成分分析法提取煤泥数据特征,融合变量之间的相关性,降低输入煤泥数据的维数[17],该过程可描述如下:
第1步:给定一个煤泥样本集X,如式(7)所示:
(7)
式(7)中,m表示煤泥样本数,t表示煤泥样本特征数,xmt表示第m个煤泥样本的第t个特征。计算X的协方差矩阵R,得到特征值[λ1,λ2, …,λt]。
第2步:计算第j个主成分的贡献率ρj以及之前k个主成分的累积贡献率(k=1,2,…,t)ρ,根据式(8)得出:
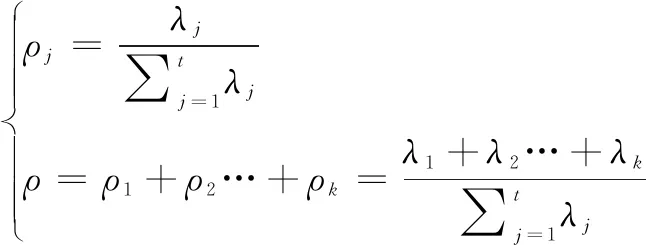
(8)
第3步:构建特征空间P=[υ1,υ2,…,υt]T,得到X=[PC1,PC2,…,PCt]。经过以上步骤的煤泥数据预处理后,选择累积贡献大于85%的前k个主成分PC1,PC2,…,PCk作为LS-SVM的输入变量。
在LS-SVM建模过程中,模型参数对模型回归的精度有重要影响,本文采用GSA对LS-SVM模型的参数进行优化,该算法不需要交叉、变异等进化算子,具有收敛速度快、不易陷入局部极小、全局搜索能力强等优点[18]。GSA描述如下:
(9)
式(9)中,G(t)是指第t次迭代时的引力常数,ε是指常参数,Rij(t)是指第i个和第j个agent之间的欧氏距离,Mi(t)是指第i个agent的惯性质量,可通过以下公式计算[20]:
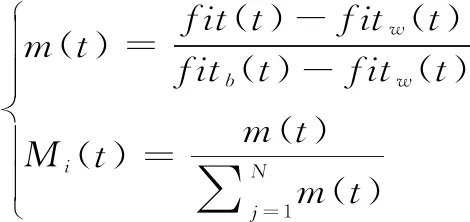
(10)
式(10)中,m(t)是指重力质量,fit(t)是指第i个agent在第t次迭代时的适应度值,fitw(t)是指最差适应值,fitb(t)是指最优适应值。在d维中,第i个agent作用引力之和为Fi(t),如式(11)所示:
(11)
式(11)中,randj是介于[0,1]之间的随机数。根据以上等式,最终得到第i个agent的位置和速度更新迭代过程,如式(12)所示[21]:
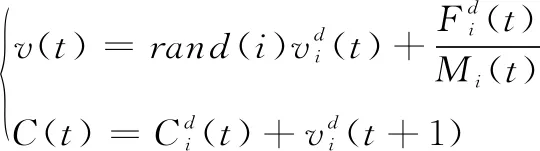
(12)
综上所述,本研究采用GSA用于优化LS-SVM模型内部参数,算法步骤如下:
第1步:初始化总体大小N=30,最大迭代次数tmax=200,常常数ε=10-6,维度d=2,随机初始化agent的位置。
第2步:以目标函数的最小值为优化目标,计算适应度值fit(t),并根据等式(10)与(11)计算计算惯性质量Mi(t)与外力的总和Fi(t)。
第3步:根据等式(12)更新agent的位置。得到优化后的LS-SVM参数值。
第4步:当达到最大迭代次数或适应值满足目标值时,停止优化过程,以获得LS-SVM的最佳参数,并根据等式(6)和(7)建立单一评估模型;否则,返回第二步。
2.3 多个LS-SVM模型更新策略与构建
为了提高单一模型的泛化能力和准确性,本文将离线训练和在线学习相结合,设计了由自动再训练和参数更新组成的模型更新策略[22]。假设煤泥浮选过程是一个具有k阶时滞的非线性系统,当系统输入为s(T)时,LS-SVM模型的评估值为o(T+k),每小时检测的相应实际产量(洁净煤灰含量)为o(T+k)。然后,实际输出和评估输出之间的相对误差RE(T+k)表达式为:
(13)
此外,反馈错误RE(T+k)与设置相对误差RE进行比较,如果RE(T+k) >RE,这意味着模型的评估能力降低,重新训练程序被激活。然后,使用新煤泥样本重新训练LS-SVM模型,并使用GSA更新内置参数,如第2.2节所述。
在选煤厂中,对于不同类别的煤,煤泥的可浮性可能不同,操作条件也存在相当大的差异[23]。考虑到这一因素,本研究提出了多个LS-SVM方法。对于每一类原煤,根据第2.1节建立了相应的基于LS-SVM的评估模型。然后,将多个单一的LS-SVM模型构造成多个LS-SVM模型,类似于建立一个大模型。该过程的主要问题是哪个单一模型需要在正确的时间运行[23],因此,需要研究一种合理的模型切换机制。
对于原煤来源不同的选煤厂,通常有两种制备模式:单一原煤制备和混合原煤制备。合理配煤可以保证产品质量,提高经济效益。实际上,不同类别的原煤通常储存在不同的原煤仓中,给煤机安装在每个煤仓下。然后,将不同等级的原煤混合在一起,运输到原煤制备车间[24],该过程如图2所示。
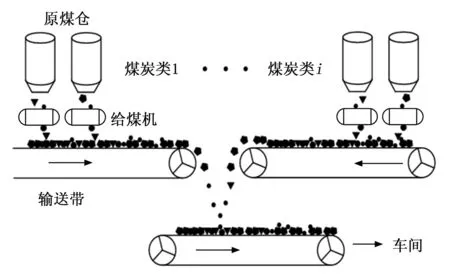
图2 配煤过程示意图
对于单一类别的煤炭洗选,通过相应的皮带运行状态直接评估煤炭类别。对于混煤洗选,通常混煤不超过3级,比例根据产品质量要求确定,并通过调整给煤机进行控制。输送带运行状态信号“I”和运行给煤机数量“m”可以用来描述配煤过程,S是相应的煤种。如果原煤类别发生变化,估计模型将切换到相应的单一LS-SVM模型。值得注意的是,选煤是一个连续的过程;当原煤类别发生变化时,应在一段时间“t”后完成模型切换,t是原煤从原煤皮带到浮选预处理器的运行时间[25-26]。综上所述,本研究所提出多个LS-SVM评估模型的结构如图3所示。
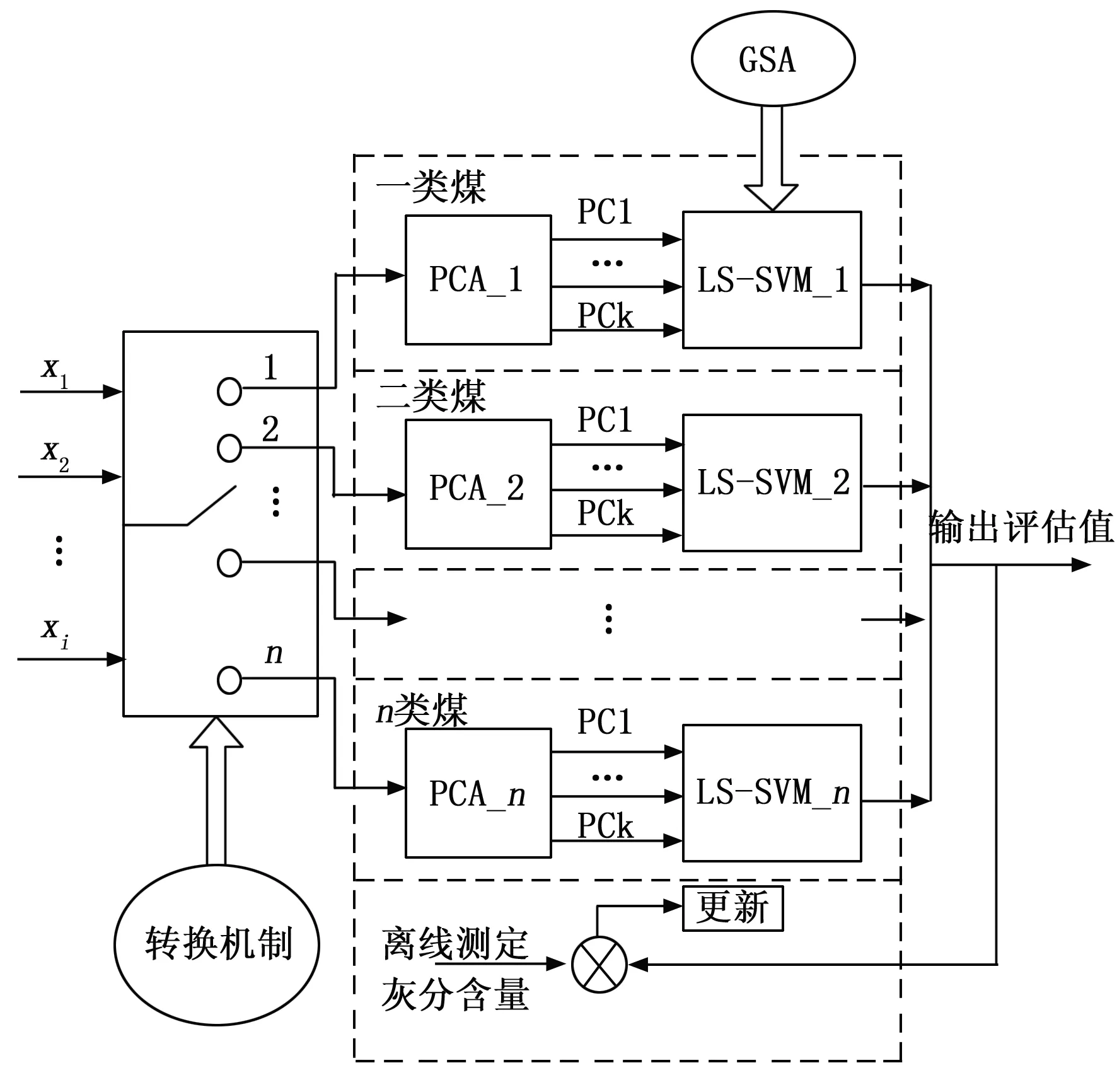
图3 LS-SVM模型结构
3 实验与分析
为了验证该研究所提出的浮选精煤灰分LS-SVM评估模型的适用性与可行性,该研究将进行展开具体实验,已在中国X市选煤厂的工业FCMC浮选柱上进行了测试。浮选柱用于分离粒度在0~0.25 mm之间的细煤泥。实验数据来自工业浮选过程,如表2所示。
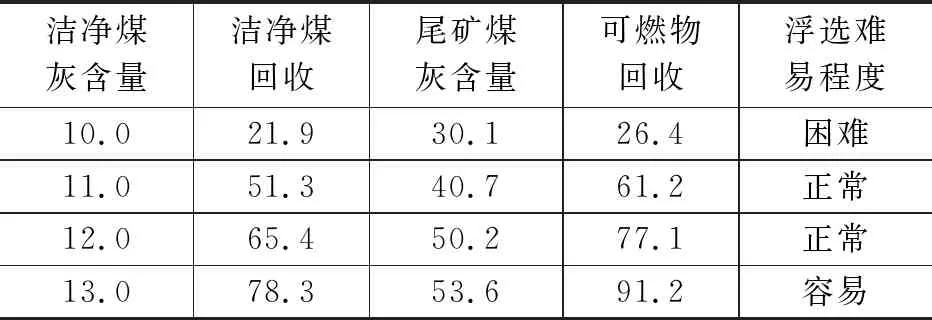
表2 煤泥浮选实验数据 %
具表2所述,在优化操作参数的基础上,根据中国标准MT259-1991对煤泥的可浮性进行了评价,将其大体上分类为一类煤(10%)、二类煤(11%)、三类煤(12%)和四类煤(13%)。表2表明,通过对X市选煤厂煤泥的筛选,综合4种煤中粒度在0.045 mm以下的煤泥比例达到68.51%,灰分含量高达40.19%,这些参数是煤泥灰分高、可浮性差的主要原因。
在本研究中,实验建模数据来自选煤厂的实际工业浮选过程,为了保证模型的稳定性和准确性,需要从工业信号中检测并去除异常值,然后对信号进行滤波。选择Pauta准则[27]作为异常检测和消除方法,过滤方法采用改进的队列平均过滤器,如式(13)所示:

(13)
式(13)中,N表示常数(此处N=20),C表示最新采样值,A表示过滤值。以煤炭一类为例,浮选过程稳定后收集数据,采用Pauta准则从稳态采集的数据中剔除异常值,选取50组样本。为了验证基于LS-SVM的单一评估模型的效果,本研究构建计算机实验测试平台,该平台的实验计算机硬件环境为Pentium(R)CPU、8核16G内存[28],电脑的硬盘容量为512 G的硬件环境,软件的操作系统Windows10,采用Matlab软件进行仿真,其架构如图4所示。
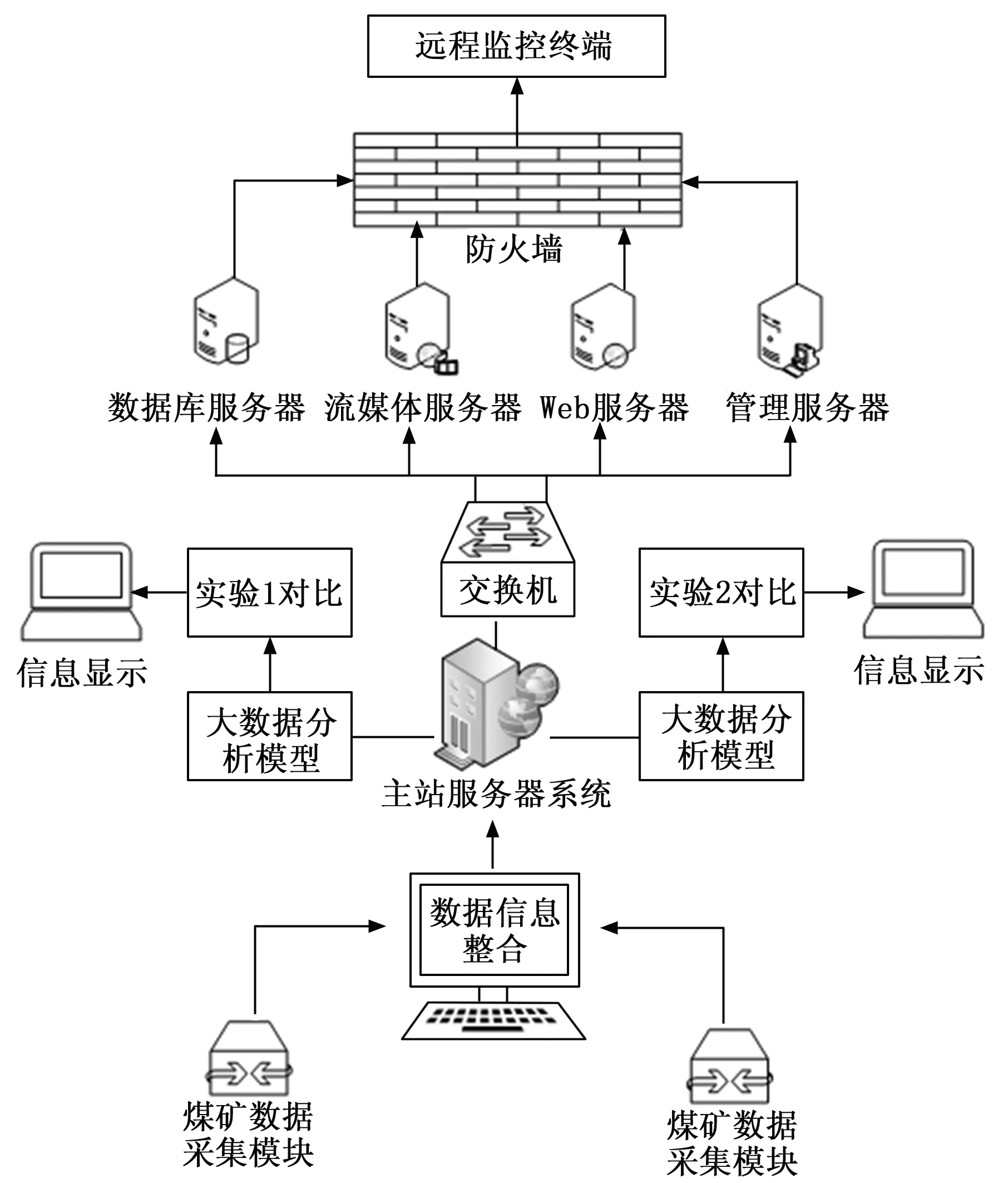
图4 计算机实验架构
此外,本研究还使用了文献[4]ANN算法模型对同一训练集的一类煤进行建模,选择均方根误差(RMSE,root mean square error)作为评估模型的性能评估指标,如式(14)所示:
(14)
从图5和表3可以看出,基于LS-SVM和ANN的单一模型都能很好地拟合测试数据,但在不同测试样本数的环境下,该研究所提出的LS-SVM算法模型的RMSE均低于文献[5]采用的ANN算法模型,能够证明LS-SVM算法模型是更好的选择,这些结果可能是由于支持向量机在小样本情况下具有很强的泛化能力。此外,如果将1类煤炭的单一评估模型应用于2类煤炭,那么LS-SVM和ANN的评估精度都会显著降低,从而使评估结果无效。
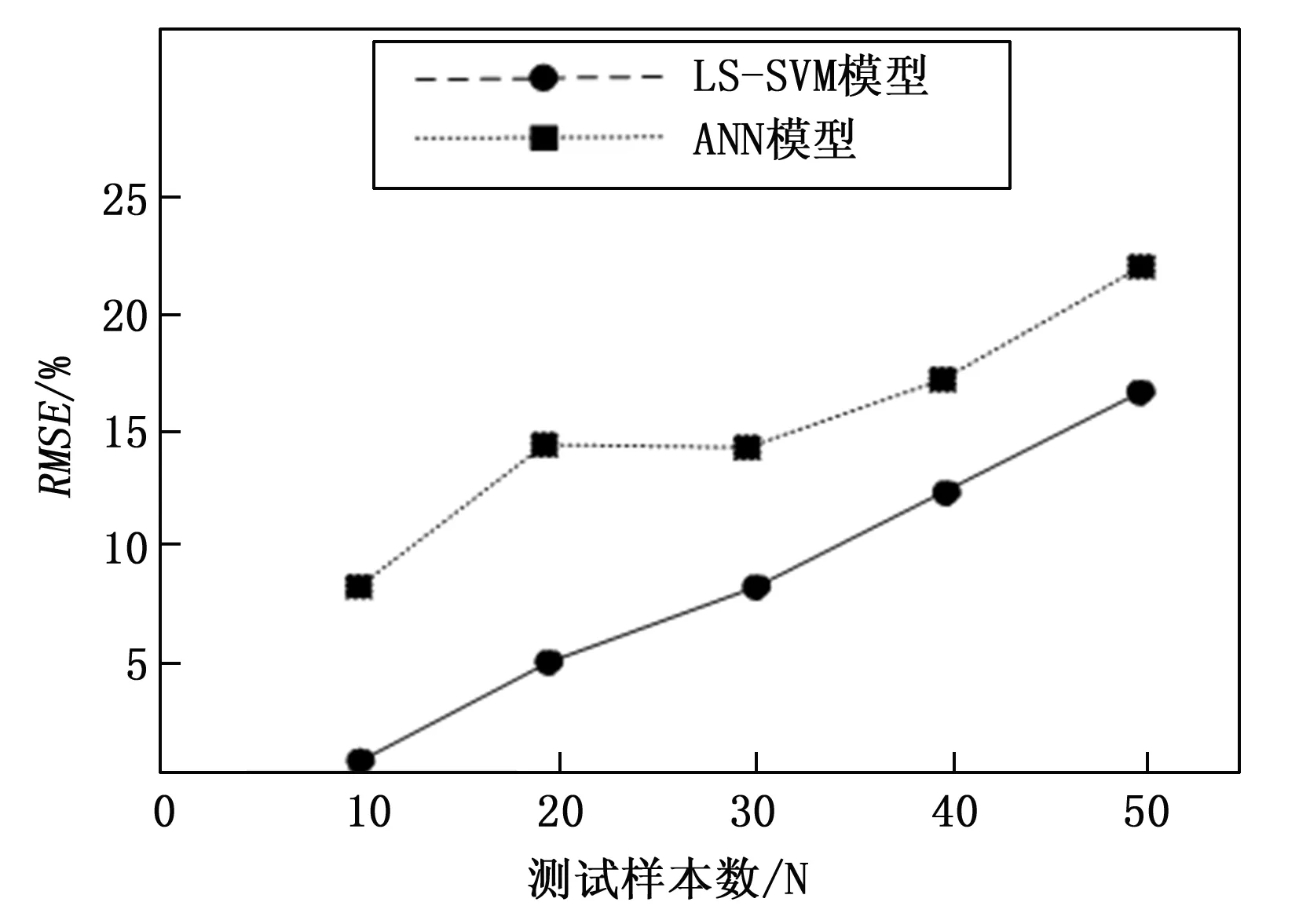
图5 两种算法模型评估性能对比
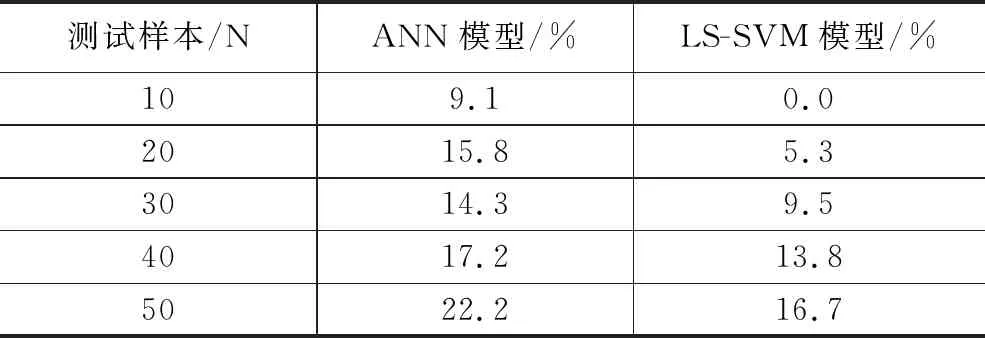
表3 两种算法模型评估性能对比
为了进一步验证本研究提出的LS-SVM评估模型的可行性,根据上述建模方法,针对不同类别的煤炭,建立了基于LS-SVM的不同单一评估模型。从2类、3类和4类煤的每个浮选过程中分别选择100组样本数据。每小时收集一次浮选精煤样本,并对灰分含量进行分析。在试验期间,原料原煤包括上述四类煤,在工业试验期间的15天内,对评估结果和操作员的化验结果进行了比较,如图6、图7所示。
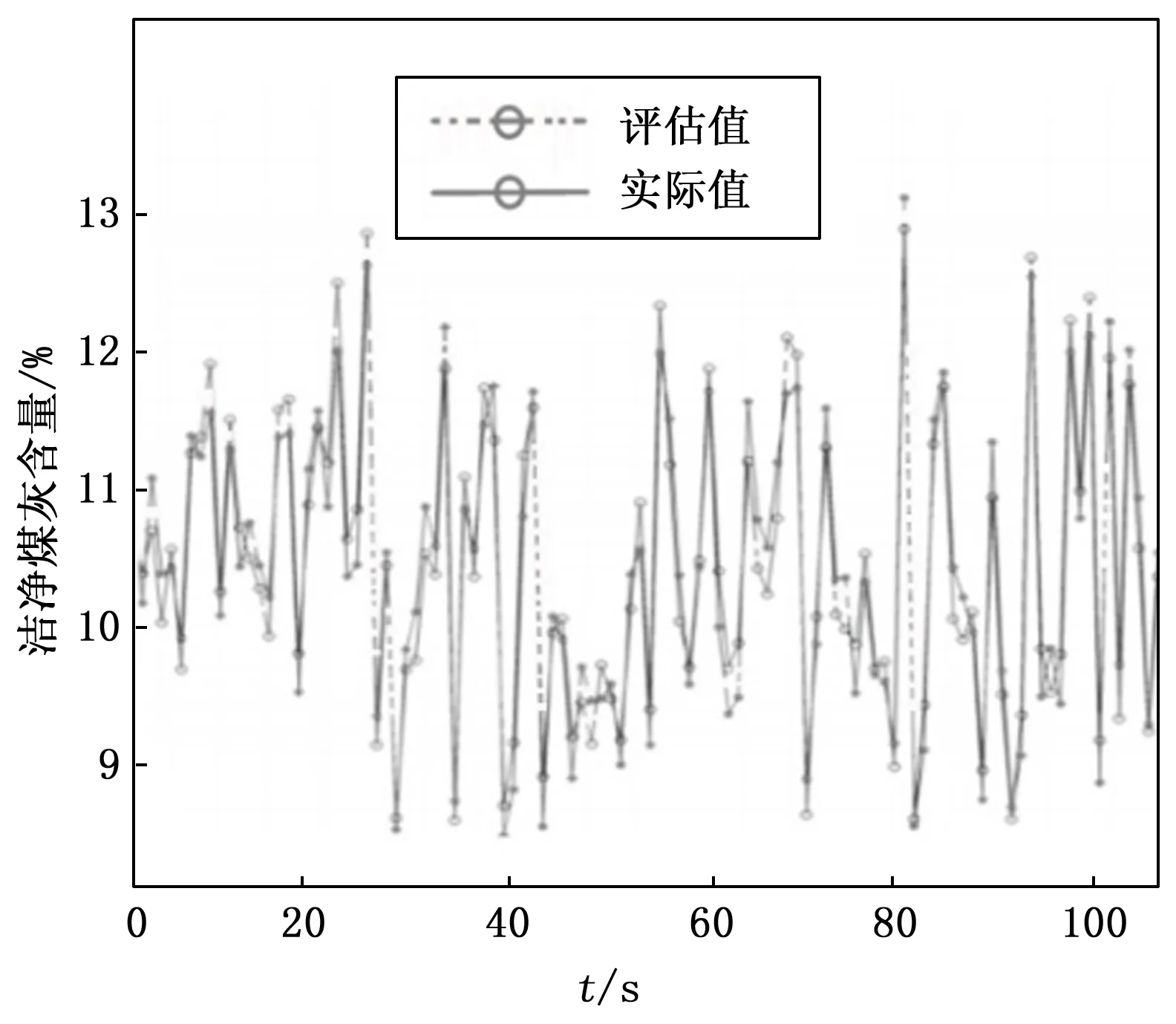
图6 工业试验中估测值与实际值的比较
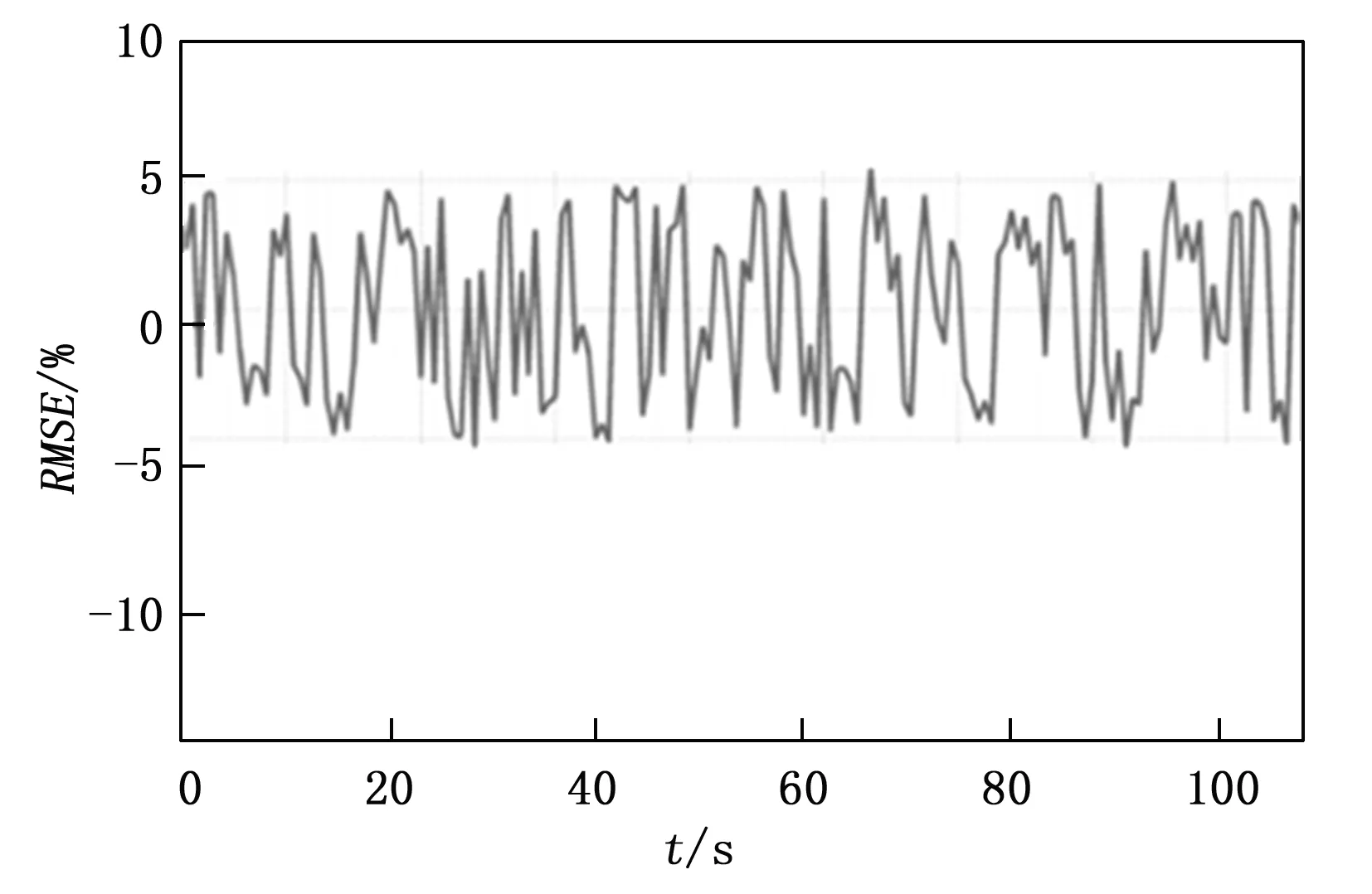
图7 工业试验中的误差分布
从图6、7中可以看出,RMSE平均值大约为3.3%,低于单一模型的12.6%,大大超出了符合预期。工业试验结果表明,该模型具有良好的评估效果和工业适用性,这种优势主要是由于以下两点:
1)对于单一类别的煤炭,由于过程中的各种干扰,静态评估模型的精度可能会随着时间的推移而降低;因此,本研究设计了一种模型更新策略来解决单一模型精度下降的问题。
2)不同煤种的可浮性以及操作条件有很大差异;因此,为了解决模型失配问题,将不同煤种的多个单一模型结合起来,建立了一个多个LS-SVM联合评估模型。上述方法提高了综合评估模型的评估精度。
4 结束语
浮选泡沫为气液固三相混合物;因此,很难在线测量洁净煤的灰分含量。本研究提出了一种基于模型更新和多重最小二乘支持向量机的煤泥浮选综合估算模型。在小样本集的情况下,支持向量机也比神经网络具有更好的估算精度和更强的泛化能力。此外,LS-SVM算法模型由于采用了结构风险最小化原理,支持向量机可以有效地避免经典学习算法中的过拟合和局部极小。算法融合了主成分分析法提取煤泥数据特征,强调算法参数之间的相关性,降低输入煤泥数据的维数,去除冗余信息,降低LS-SVM的计算复杂度,同时保留最大的数据信息。在本研究中,LS-SVM被引入到煤炭浮选过程中洁净煤灰含量的估算中,通过实验证实了该方法的可靠性。然而,本研究发现还有一些问题直接影响到煤泥浮选估算模型的准确性、稳定性和适用性,例如,工作条件的波动、原材料的异质性和原材料类别的变化等,未来会针对这些因素影响效果进一步地研究。

