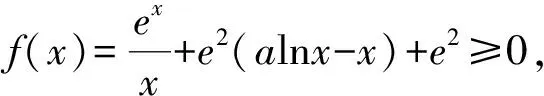一道函数不等式问题的探究与思考

福建省厦门市海沧中学 (361022) 徐云龙 陈凌燕

导数作为研究函数的一个有力工具，是高中阶段学习的重要内容，同时也是考查学生核心素养和创新意识的重要载体.本文通过对一道函数不等式的证明探究，来分析一类导数试题的求解方法和命制手法.

1试题及解法

考查意图：本题以指数和对数混合的函数为载体，研究含参不等式的恒成立问题，较好地考查了导数在研究函数性质中的应用等基础知识，体现学生逻辑分析，运算求解等关键能力.试题简洁而内涵丰富，给解题者以数学美的感受.

解法一：直接对函数f(x)求导，利用导数研究函数f(x)的单调性求最小值.

若00，g(x)单调递增，g(x)>g(0)=1；

若1lna时，g′(x)>0，g(x)单调递增.

所以g(x)min=g(lna)=a-alna.

所以，当10；当a=e时，g(x)≥g(x)min=g(1)=0；当e0，g(4)=e4-4a≥e4-4e2>0，所以g(x)存在两个零点x1,x2(01时，f′(x)>0，f(x)单调递增，所以f(x)min=f(1)=e-a≥e-a≥0>-e2；当e

设h(a)=a-alna(e

评析：本解法将不等式恒成立问题转化为函数的最值问题，这是不等式恒成立问题的通法，但运算过程较为繁琐，对学生的运算能力有较高的要求.

解法二：变换主元，利用a的取值范围对f(x)进行放缩.

综上，当0

当00，则g(t)min=g(e)=e-a≥e-e2>-e2；当e

解法五：分析法，同构换元齐上阵.

评析：上述解法综合利用了解法二的变换主元和式子的结构特征，进行换元化简，简化运算，同时可得本题的起源于常见不等式et≥t+1.从而拨开云雾见真章，认识到本题的命制方法.

2命题思考

下面证明：当a>e2时，∃x0∈(0,+∞)，使得f(x)≥0不成立.

综上，若f(x)≥0恒成立，则有a≤e2.

下面证明：当a<1时，∃x0∈(1,+∞)，使得f(x)≥0不成立.

由导数知识知方程x-lnx-2=0,x∈(1,+∞)有解，设为x0，即x0-lnx0-2=0且x0>2.所以ex0-lnx0-2-(x0-alnx0-1)=(x0-2)(a-1)<0.综上，若f(x)≥0恒成立，则有a≥1.

3类题再现

题目1 (2019年福建省质量检测理科21题)已知函数f(x)=x(e2x-a).(1)若y=2x是曲线y=f(x)的切线，求a的值；(2)若f(x)≥1+x+lnx，求a的取值范围.

简析：(1)略；(2)由x(e2x-a)≥1+x+lnx，得e2x+lnx≥ax+x+lnx+1.令t=2x+lnx，由不等式et≥t+1，得e2x+lnx≥2x+lnx+1，当a≤1时，有e2x+lnx≥2x+lnx+1≥ax+x+lnx+1，即a≤1时，不等式恒成立.

下面证明：当a>1时，∃x0∈(0,+∞)，使得f(x0)≥1+x0+lnx0不成立.

由导数知识知方程2x+lnx=0有解，设为x0，即2x0+lnx0=0，则有e2x0+lnx0-(ax0+x0+lnx0+1)=(1-a)x0，因为a>1，x0∈(0,+∞)，所以(1-a)x0<0，即f(x0)<1+x0+lnx0.

综上，若f(x)≥1+x+lnx，则有a≤1.

试题1的由来：首先由常见不等式et≥t+1，换元令t=2x+lnx，得e2x+lnx≥2x+lnx+1，若e2x+lnx≥2x+lnx+1≥(a+1)x+lnx+1，得a≤1.(当然，本题还需证明，当a<1时，不等式不成立)

题目2 (2020年全国新高考Ⅰ卷第21题)已知函数f(x)=aex-1-lnx+lna.

(1)当a=e时，求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积；

(2)若f(x)≥1，求a的取值范围.

简析：(1)略；(2)由f(x)=aex-1-lnx+lna≥1得elna+x-1+lna+x-1≥lnx+x.由lnx+x=elnx+lnx，得elna+x-1+lna+x-1≥elnx+lnx.

令g(x)=ex+x，由g′(x)=ex+1>0，得lna+x-1≥lnx，lna≥lnx-x+1，不难得h(x)=lnx-x+1的最大值为0，所以lna≥0，即a≥1.

试题2的由来：首先由常见不等式x-1≥lnx，若x-1+lna≥lnx恒成立，则有lna≥1，即a≥1.由g(t)=et+t单调递增得ex-1+lna+x-1+lna≥elnx+lnx，即f(x)=aex-1-lnx+lna≥1.

题目3 (2013年课标全国Ⅱ卷第21题)已知函数f(x)=ex-ln(x+m).

(1)设x=0是f(x)的极值点，求m，并讨论f(x)的单调性；

(2)当m≤2时，证明：f(x)>0.

简析：(1)略；(2)由不等式ex≥x+1，当且仅当x=0时取等号；又有ln(x+m)≤x+m-1，当且仅当x+m=1时，取等号；由m≤2，得x+1≥x+m-1，即ex≥x+1≥x+m-1≥ln(x+m)，由不等式不能同时成立，得ex>ln(x+m)，即f(x)=ex-ln(x+m)>0.

题目4 (2022莆田高三三检第22题)已知函数f(x)=ex-ax(a∈R).

(1)讨论f(x)的单调性；

(2)若a=0，证明：对任意的x>1，都有f(x)≥x4-3x3lnx+x3.

试题4的由来：首先由常见不等式et≥t+1，换元令t=x-3lnx，得ex-3lnx≥x-3lnx+1，即ex≥x4-3x3lnx+x3.

4教学反思

追求通法，但更要认识问题本质.不等式恒成立问题的通法是转化为求函数的最值问题.通法往往运算复杂，同时也易将问题的本质掩盖在复杂的运算之中，难以发现.因此，我们要对问题进行更加深入的思考，加强对问题本质的认识，厘清问题的本质，也就认识了题目的来龙去脉，认识了题目是如何被命制出来的，做到了解一题通一类，提升了素养和思维的深度，也使学生感受到学习数学的乐趣.