改进滑模观测器的高速永磁同步电机矢量控制

郭炎龙，王贞艳，何延昭

(1.太原科技大学 电子信息工程学院，太原 030024；2.北京轩宇空间科技有限公司，北京 100190；3.北京控制工程研究所，北京 100190)

高速永磁同步电机(high speed permanent magnet synchronous motor，HSPMSM)具有体积小、效率高、功率密度大、转动惯量小、动态响应快、调速范围宽、机械振动和噪声小，以及相对高速无刷直流电机转矩脉动小等优点[1-2]。高速永磁同步电机想要达到高性能控制，需要依靠精确的位置信息，但机械传感器的安装又受限于成本和工作环境，因此对高速永磁同步电机进行无位置传感器控制研究既具有工业应用价值又具有理论参考意义。

目前常用的无位置传感器转子位置检测方法主要有适用于低速的高频信号注入法[3-5]和基于反电动势估计的模型参考自适应法[6]、滑模观测器法、扩展卡尔曼滤波器法[7]和状态观测器法。其中，滑模观测器法有着不受电机参数影响、结构简单、鲁棒性强的优点。

传统的滑模观测器使用符号函数作为滑模开关函数，然后用低通滤波器提取出高频开关信号中的反电动势信号，通过反正切函数提取出转子的位置信息[8-9]。由于传统滑模观测器采用符号函数，反电动势信号包含在高频的开关信号里，要使用低通滤波器来提取反电动势信号，这会造成相位滞后，需要进行相位补偿，同时，传统滑模观测器的滑模增益一般是凭借经验给的定值，这会加大获得的转子位置的抖振程度。文献[10]提出了结合模糊控制来调节滑模增益的模糊滑模观测器，有效减小了系统抖振。文献[11]提出了一种新的趋近律。在纯指数趋近律上，引入终端吸引子的概念，形成终端吸引子逼近方法，有效地削弱了滑模固有的抖振，加快了趋近速度。文献[12]提出了一种变指数趋近率，把变指数项加入到双幂次趋近律中，改变了双幂次趋近律的趋近速度，削弱滑模系统自身的抖振。文献[13]使用了软件锁相环来提取转子位置。文献[14]提出了一种变边界层切换函数，通过使状态误差切换至小边界层来减少抖振现象并提高转子位置和转速的观测精度。但是这些方法在改善转速、估计精度的同时也带来了算法的复杂性问题。

针对这些问题，本文提出一种改进滑模观测器，引入与转速相关的自适应滑模增益，并从中推导出了包含转子位置信息的转子磁链估计值，但此时得到的转子磁链估计值中仍含有高频分量，通过设计自适应转子磁链观测器，来获得更加平滑的转子磁链估计值，然后使用锁相环提取转子位置信息。最后仿真验证了所提方法的可行性和有效性。

1 高速永磁同步电机的数学模型

静止参考系(α，β轴)下的表贴式高速永磁同步电机模型如下：

(1)

其中iα、iβ、uα、uβ和eα、eβ分别是定子电流、定子电压和反电动势，Rs是定子电阻，Ls是定子电感，ψf是永磁体的磁链幅值，we是电角速度，θ是电机转子位置。

从式(1)中可以看出，反电动势中带有转子的位置信息，所以，可以通过观测反电动势来获得转子的位置信息。

2 传统的滑模观测器

依据滑模变结构理论，选取滑模面为

(2)

设计滑模观测器模型为

(3)

其中us=[uα，uβ]T，k为滑模增益，sgn为符号函数。

用(3)-(1)得到电流的误差方程为

(4)

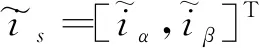
为了使系统可以进入滑动模态，构造Lyapunov函数

(5)

则滑模观测器的稳定性条件为：

(6)

推出稳定条件为：

k>max(|eα|，|eβ|)

(7)

因此只要k足够大，就可以保证系统发生滑模运动，同时保证滑模运动在全局范围内的渐近稳定，根据控制理论里的等效控制可得：

(8)

此时得到的反电动势中包含在大量的高频开关信号中，需要用低通滤波器滤除这些高频信号。然后通过反正切函数得到转子位置。

(9)

传统的滑模观测器原理框图如图1所示。

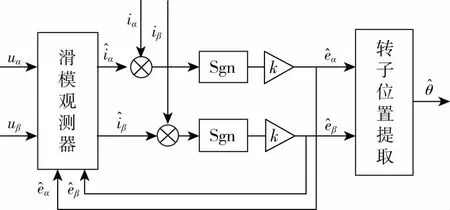
图1 传统滑模观测器

3 改进滑模观测器

3.1 改进滑模观测器的设计

为了减小抖振，使用sigmoid函数代替开关函数sgn，即：

(10)

由式(1)可知反电动势的大小与转速有关，因此随着转速的升高，需要的滑模增益越大，如果滑模增益为较大的定值，势必加剧在低速段的抖振，而且，反电动势的大小随转速变化，这使得观测的反电动势中含有噪声。

为了解决这些问题，引入与转速相关的自适应滑模增益，得到转子磁链的观测值，转而从转子磁链中获取转子位置信息。优化的滑模观测器如图2.

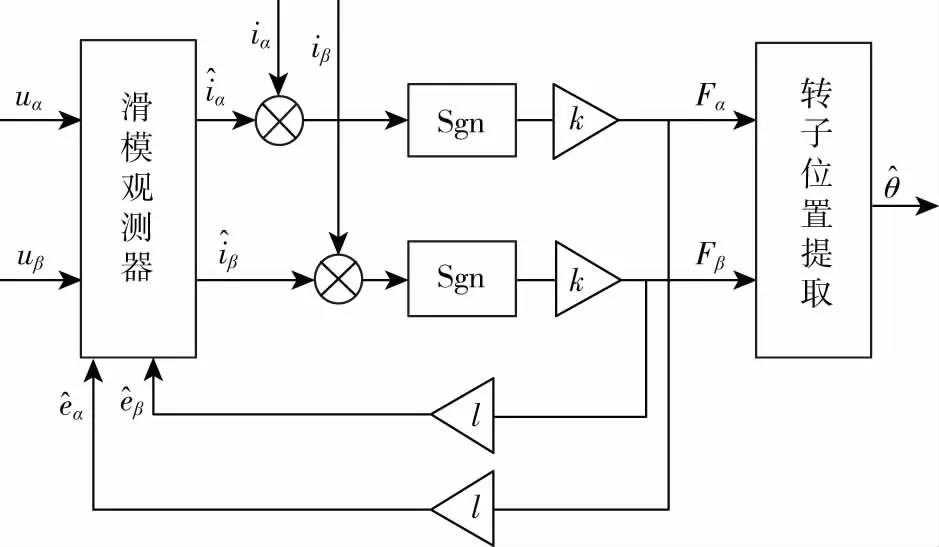
图2 优化的滑模观测器

(11)

其中，c为一个很小的常数，防止转速为零时，滑模增益为零。Fα、Fβ为转子磁链。

此时的滑模观测器模型变为：

(12)

那么得到的反电动势变为：

(13)

从图(2)可以看出没有使用反电动势来估算转速，而是获得了转子磁链观测值，再从中估算转速。

(14)

当c足够小时

(15)

3.2 转子磁链观测器设计

这样获得的转子磁链中仍含有一定的高频分量，在传统的滑模观测器中通常使用一阶低通滤波器滤除这些高频信号，从而导致相位延迟，为了完全补偿相位延迟，需要实时的使用转子的角速度信息，受到角速度估计误差的影响，导致补偿效果变差，为了避免使用低通滤波器，设计转子磁链观测器来提取转子磁链信号，以估计转子位置信息。

转子磁链表达式为

(16)

(17)

在此基础上构造转子磁链观测器

(18)

由于机械时间常数远大于电气时间常数，所以认为转速在一个估算周期内不变，则

(19)

为了证明转子磁链观测器的稳定性，构造李雅普诺夫函数为

(20)

(21)

将式(19)代入式(21)得

(22)

可以从上述方程看出只要n为正数，转子磁链观测器就是渐进稳定的。

3.3 转子位置估算

采用锁相环原理来估算转子位置，锁相环结构框图如图3所示。

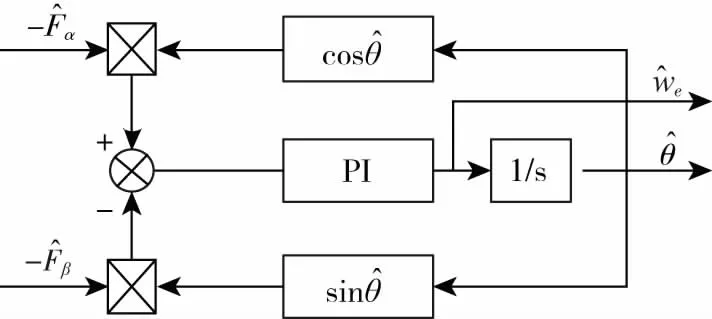
图3 锁相环结构图

(23)

将得到的转子位置误差送入PI环节，通过调节合适的PI参数，就可以得到估计的转子转速，再对转速进行积分就可以得到估计的转子位置。

4 仿真实验

为了验证本文所设计的改进滑模观测器，在Matlab/simulink(R2018a)仿真软件中搭建仿真模型，选用id=0的HSPMSM矢量控制系统仿真模型，控制系统整体框图如图4所示。

图4 HSPMSM矢量控制系统仿真模型

仿真所用的电机参数为R=0.122 Ω，L=0.675 mH，ψf=0.040 6 Wb，J=0.001 79 kg·m2，极对数p=2.

将转速给定为1 000 r/min，图5为给出了采用sigmoid函数、滑模增益为定值(这里设定为30)的滑模观测器仿真结果。图6为采用sigmoid函数和自适应滑模增益的滑模观测器仿真结果。

对比图5(b)和图6(b)，可以看出采用自适应滑模增益可以有效减小抖振，降低转速估计误差。

图5 采用sigmoid的滑模观测器仿真

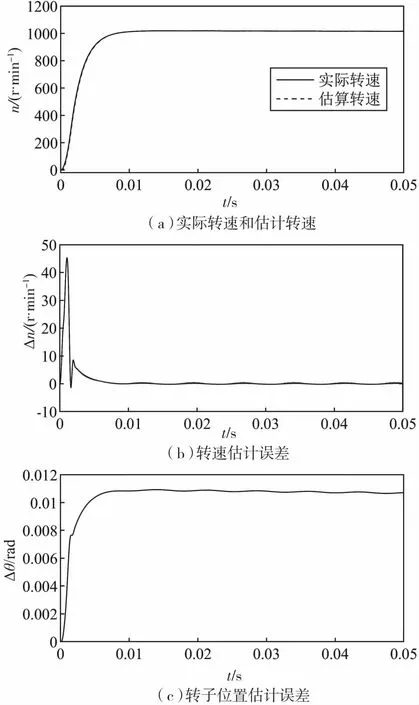
图6 采用sigmoid和自适应滑模增益的滑模观测器仿真

将转速设定为斜坡给定，在2 s转速到达10 000 r/min，在4.5 s转速到达20 000 r/min.图7给出了采用sigmoid函数和自适应滑模增益仿真结果。

从图7中可以看出，即使采用了自适应滑模增益，转子误差仍随着转速的升高而升高，在2 s转速到达10 000 r/min，转速误差为±0.4 r/min，在4.5 s转速到达20 000 r/min，转速误差为±1.5 r/min.

图7 采用sigmoid和自适应滑模增益的滑模观测器仿真

这是由于获得的转子磁链中仍含有高频分量，为了解决这个问题，设计转子磁链观测器来滤去这些高频分量，图8给出采用转子磁链观测器的滑模观测器仿真结果，磁链观测器的系数设置为10 000.

从图8(a)，8(b)中可以看出，在2 s转速到达10 000 r/min，转速误差为±0.4 r/min，在4.5 s转速到达20 000 r/min，转速误差为±0.5 min.

从图8(e)，8(g)中可以看出，转子磁链观测器观测到的α轴磁链的THD(Total Harmonic Distortion)相比直接得到的转子磁链减小了0.02%.设计的转子磁链观测器可有效滤除高频分量，减小转速误差。

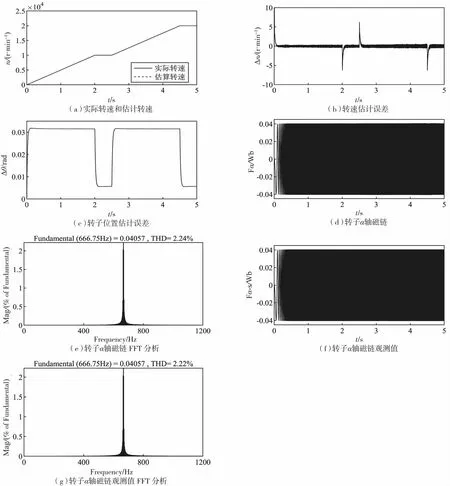
图8 采用转子磁链观测器的滑模观测器仿真

图9给出了带风机负载(转矩与转速的平方成正比)时的仿真波形，在2.7 s处电机转速稳定为20 000 r/min时，负载转矩为1.6 N·m.

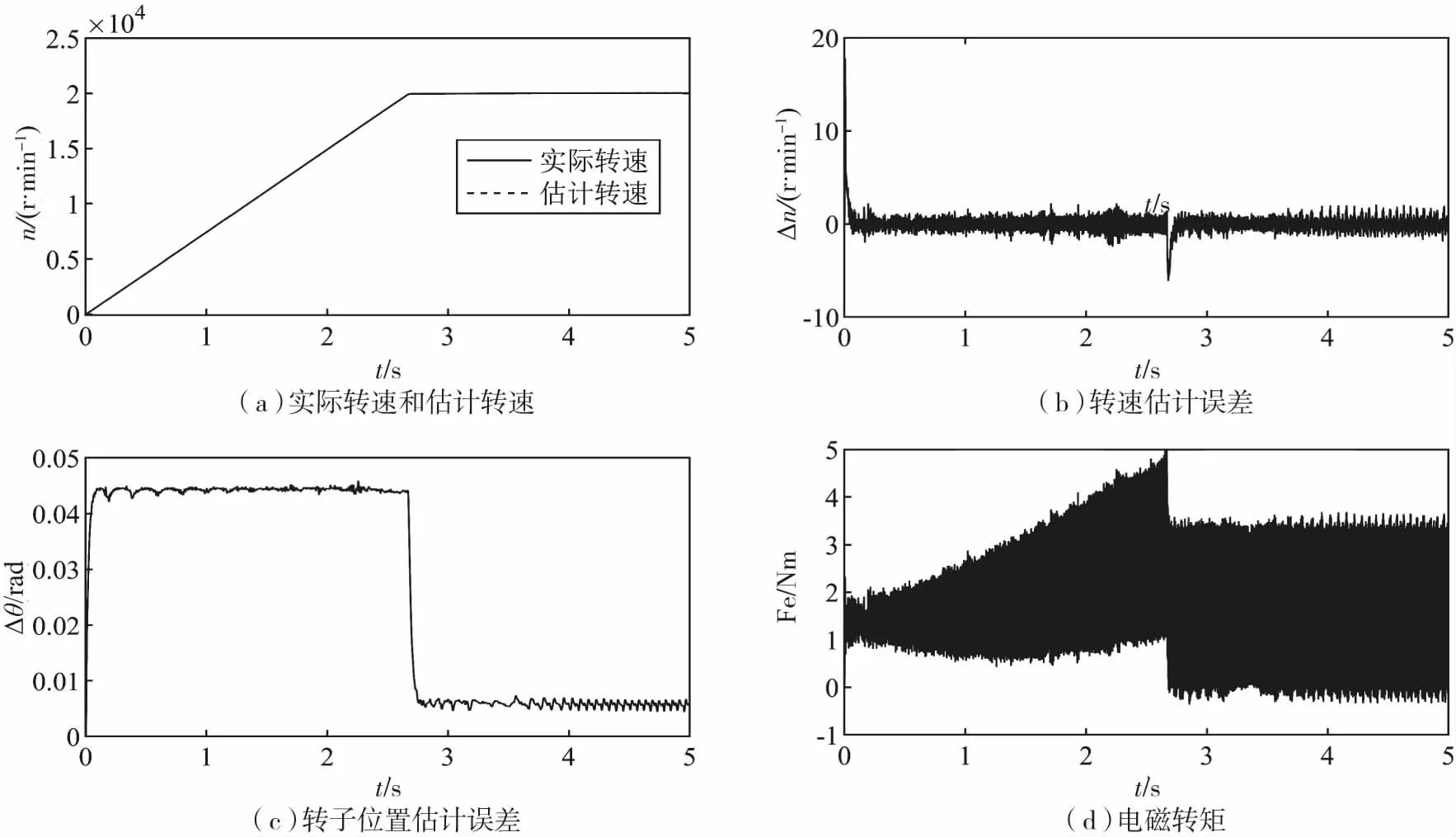
图9 带风机负载的改进滑模观测器仿真

5 结论

提出了一种改进滑模观测器，通过引入与转速相关的滑模增益，减小了系统的抖振，同时获得了转子磁链值，但得到的转子磁链值中仍含有高频抖振，这些高频抖振会增大速度估计误差，为了消除转子磁链观测值中的高频抖振，设计自适应转子磁链观测器，最后通过锁相环提取转子位置。仿真结果验证了本文所提方法的可行性和有效性。