针对线性调频雷达系统的信源数估计算法
王浩丞
(电子信息控制重点实验室,四川 成都 610036)
0 引 言
随着电子技术的发展,雷达系统发射的信号逐渐被加入各类调制,最常见的雷达信号体制就是线性调频信号体制[1-3]。
同时,随着电子对抗技术的发展,特别是各类反辐射武器的发展,雷达系统为提高自身防护能力通常会加装诱饵。雷达加装诱饵后,通过诱饵信号掩护雷达信号,致使反辐射武器作战效能下降,甚至失效[4-6]。
为对抗雷达诱饵,反辐射导引头可采用空间谱估计算法提升抗诱饵能力,而谱估计算法需要使用雷达、诱饵数量进行超分辨[7]。但直接采用谱估计算法进行雷达、诱饵数量估计存在以下不足:
(1) 根据谱估计算法原理,如果雷达加诱饵数量为N,则理论上至少需要导引头有N+1个阵元和通道进行接收处理才可实现雷达、诱饵数量估计,对导引头通道要求较多,系统较为复杂。
(2) 通过谱估计算法识别雷达诱饵数量,其识别的准确度与雷达诱饵工作频段、雷达与诱饵的角度差、导引头天线阵尺寸相关。雷达诱饵工作频段越低,雷达与诱饵的角度差越小,谱估计所需天线阵尺寸越大,导引头识别雷达诱饵数量越难,甚至无法识别雷达诱饵数量,对导引头尺寸要求较大。
(3) 谱估计算法涉及大量矩阵运算,运算复杂度高,对导引头硬件资源、功耗要求较高,且快速性、实时性较差。
针对谱估计算法在反辐射导引头应用中对硬件、尺寸、资源要求较高,且速度较慢的问题,本方法利用线性调频信号雷达发射信号的前、后沿特征,构造匹配函数,进行匹配滤波,提供一种不受孔径、距离限制,可以快速、准确识别雷达、诱饵数量的新方法。
1 攻击目标场景
雷达阵地中雷达与诱饵的典型分布如图1所示。1部雷达一般配有2~3个诱饵。雷达距离诱饵一般在300~1 000 m范围内。
为避免雷达信号暴露出来,诱饵信号前后沿需遮盖雷达信号的前后沿,诱饵超前时间一般超前μs量级。超前诱饵出现的规律通常有3类:诱饵前沿固定超前、诱饵慢速闪烁、诱饵快速闪烁。图2所示为雷达和诱饵信号时序关系。

图2 雷达和诱饵信号时序关系
同时为使反辐射导弹攻击点尽量远离雷达,要求诱饵信号能量大于雷达信号能量,使合成能量中心尽量靠近诱饵。要求诱饵信号能量大于雷达天线主瓣的信号能量是不可能的,但由于反辐射导弹最后攻击雷达时,都是在雷达顶空或从雷达波束高仰角副瓣进入攻击,而且先进雷达都是采用低副瓣天线,副瓣电平很低,因此可以较容易地做到诱饵的信号能量高出雷达高仰角副瓣信号能量2~3 dB。
2 快速雷达诱饵数量估计方法
2.1 信号特征分析
针对线性调频信号体制雷达,雷达配装诱饵后,为保护雷达信号,诱饵发射与雷达信号样式相同的信号。同时,诱饵信号覆盖雷达信号的前后沿,保证雷达信号不被直接侦收到。由于诱饵布置在不同的位置上。反辐射导引头侦收到的雷达、诱饵信号的时序关系与导引头位置相关,通常导引头收到信号的前沿、后沿为单独诱饵信号,信号中部为雷达与诱饵的混合信号。
基于以上特征,根据前、后沿信号特征,进行线性调频信号调频斜率预测,构造匹配函数,进行匹配滤波可以实现雷达、诱饵信号的快速、准确估计。
2.2 基于调频斜率预测的诱饵数量估计方法
假设一个雷达与诱饵的发射信号为s(t),由于发射时序和位置差异,到达设备的混合信号为:
(1)
式中:n为诱饵数量;τ为诱饵与雷达信号的延时差。
由于存在延时差,则混合信号的前沿、后沿通常有部分信号为单一诱饵信号。
基于调频斜率预测的诱饵数量估计方法流程如图3所示,过程如下:
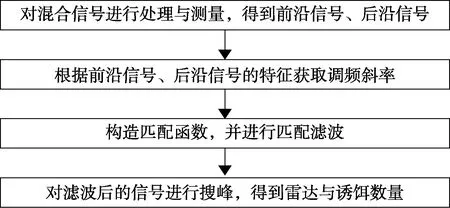
图3 基于调频斜率预测的诱饵数量估计方法流程图
(1) 测量接收到的雷达、诱饵混合信号s(t),获得其频率F0、脉宽τPW;
(2) 对接收到的雷达、诱饵混合信号进行滑窗幅相处理,获取前沿、后沿信号及其宽度;
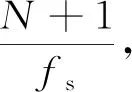

(5) 对信号前沿斜率和信号后沿斜率进行加权处理,得到准确的调频斜率,加权处理方法为:
K=w(τPWB,AB)×KB+w(τPWE,AE)×KE
(2)
式中:K为准确的调频斜率;w(τPWB,AB)为信号前沿宽度、幅度相关的加权因子,w(τPWE,AE)为信号后沿宽度、幅度相关的加权因子,KB、KE分别为信号前沿、信号后沿的预测斜率;
(6) 根据混合信号的脉宽τPW,前、信号后沿宽度τPWB、τPWE估计得到雷达信号脉冲宽度τPW0=τPW-τPWB-τPWE;根据调频斜率K、雷达信号脉冲宽度τPW0构建斜率-K的匹配函数。
(7) 利用匹配函数进行匹配滤波,输出信号为s0(t);
(8) 对s0(t)进行搜峰,如果有N个峰存在,则可判定雷达加诱饵数量为N。
3 仿真结果
3.1 仿真场景和条件假设
仿真计算设置场景如图1所示,雷达与诱饵的位置分别为:雷达(0,0,0),诱饵1(500,0,0),诱饵2(300,200,0),诱饵3(300,-200,0);导弹(导引头)从点(100 000,0,10 000)向雷达运动,运动到点(10 000,0,10 00);雷达与诱饵发射线性调频信号,信号带宽为50 MHz,脉宽为20 μs。
雷达与诱饵信号发射时序如图4所示,4个诱饵前后沿覆盖雷达前后沿,其中诱饵1信号超前雷达信号4 μs,诱饵2信号超前雷达信号2 μs,诱饵3信号滞后雷达信号2 μs。

图4 雷达与诱饵混合信号时序图
3.2 从诱饵数量估计仿真结果
仿真得到导弹(导引头)不同弹目距下收得的雷达、诱饵混合信号s(t),以其中一个弹目距为例,如图5所示。
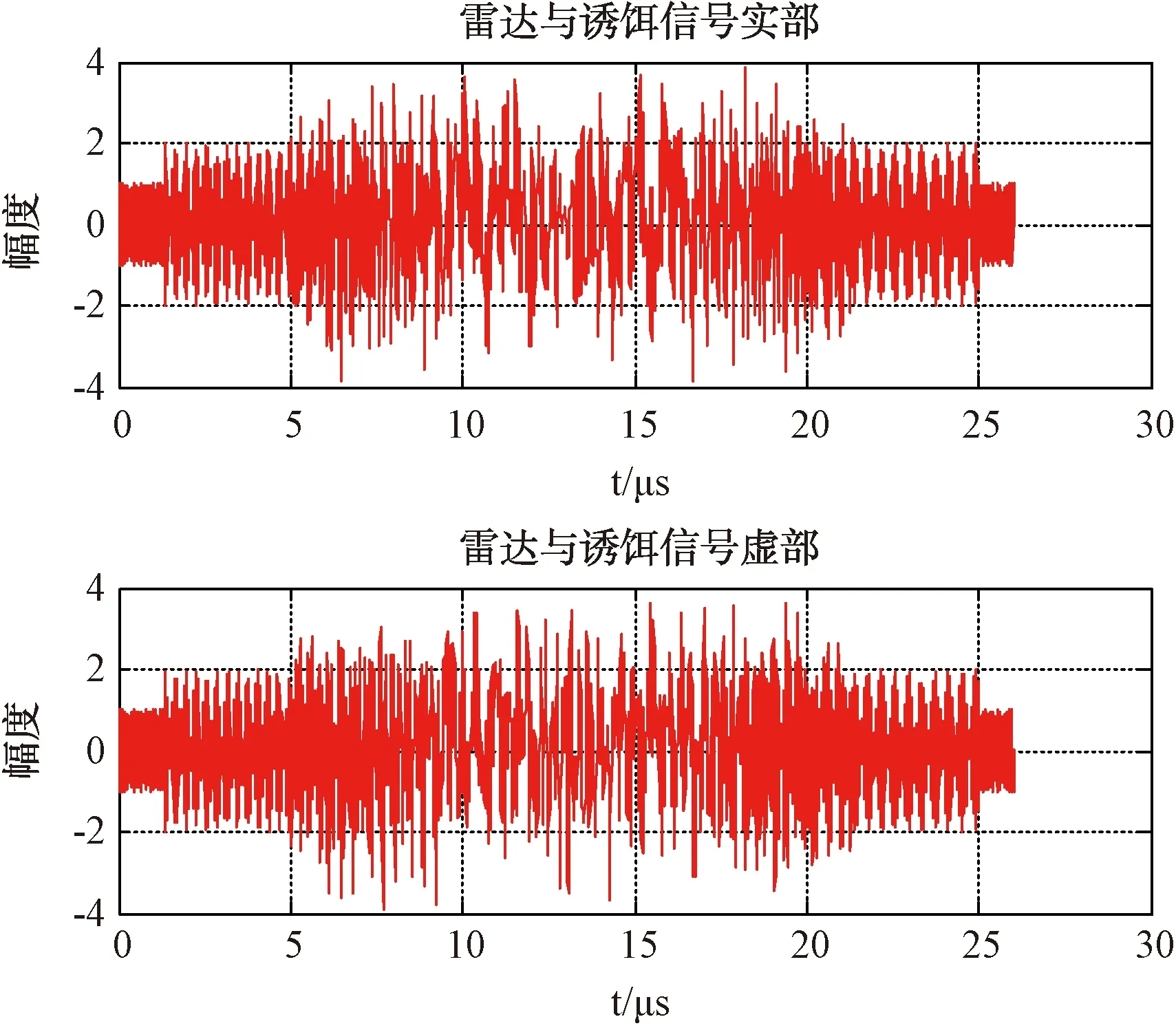
图5 接收到的雷达与诱饵信号波形图
具体识别过程如下:
(1) 测量混合信号s(t),获得其频率f0、脉宽τPW。
(2) 对混合信号s(t)滑窗幅相处理,分别获取信号前沿、后沿及其宽度τPWB、τPWE。
(3) 分别对信号前沿、后沿进行调频斜率测量,得到KB、KE。
(4) 对信号前沿、信号后沿的斜率进行加权计算。
K=w(τPWB,AB)×KB+w(τPWE,AE)×KE
(3)
式中:w(τPW,A)是与信号前沿、信号后沿的宽度、幅度相关的加权因子。
(5) 根据混合信号脉冲宽度τPW,信号前沿、信号后沿的宽度估计雷达信号脉冲宽度τPW0=τPW-τPWB-τPWE。
(6) 根据K、τPW0构建斜率-K的匹配函数H0(t),如图6所示。
(7) 利用匹配函数H0(t)进行匹配滤波,输出信号为s0(t),如图7所示。
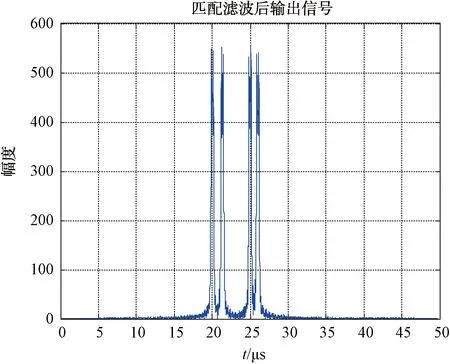
图7 匹配滤波后输出信号图
(8) 对s0(t)进行搜峰,搜峰得到有N个峰存在,可判定雷达加诱饵数量为N。按照上述步骤根据导弹位置从100 km到10 km进行201次仿真,仿真结果如图8所示,均可正确识别雷达、诱饵数量。
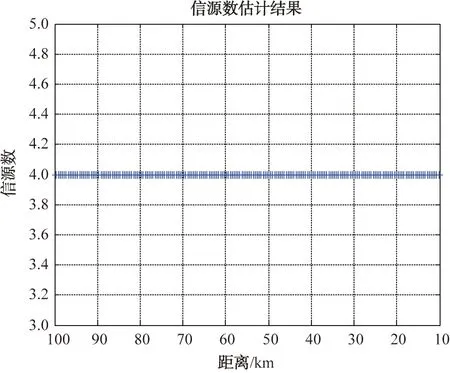
图8 雷达诱饵数量估计结果
由上述验证可见,本方法不受孔径、距离限制,只需一个接收通道,算法运算量小,速度快,可以快速、准确地识别雷达、诱饵的数量,对诱饵数量估计的准确性、快速性优于谱估计方法。
4 结束语
与现有谱估计方法相比,本方法对雷达诱饵数量的识别不受导引头频段、口径限制,即使在小口径下,也能识别低频段雷达诱饵的数量;且该方法不受弹目距影响,即使在远距离也可以准确识别雷达诱饵数量;也不受接收处理通道数限制,即使只有1个接收处理通道,也可以实现对雷达诱饵数量的判断、识别;相比8通道谱估计,系统复杂度可降低90%。

