大跨度无支撑甲板拓扑-尺寸-材料联合优化设计

崔宇朋 余 杨 余建星 李振眠

1.天津大学水利工程仿真与安全国家重点实验室，天津，300072

2.天津大学天津市港口与海洋工程重点实验室，天津，300072

0 引言

作为船体主要承重构件，大跨度甲板常被应用于油船、滚装船、舰船等，具有跨度大、无支撑等特性，其刚度、变形及动态振动性能值得关注[1]。目前，加筋板结构前期设计(概念设计)存在依赖工程经验、设计周期长及性能非最优等问题。近年来，拓扑优化(topology optimization，TO)技术飞速发展，它可在满足结构目标函数及约束条件下实现设计域中材料的最优分布以最优化结构性能，具有低成本、高收益、快速性等优点[2]，是结构概念设计最有效的手段。

发展至今，拓扑优化理论已较为成熟[3-6]，被广泛应用于船舶结构的拓扑优化设计。高上地等[7]结合形状优化和拓扑优化方法解决了角隅结构的应力集中问题，并寻优得到新型肘板结构。张聪等[8]基于变密度法实现了强度性能要求下的三体船舱壁轻量化设计。针对常规加筋板结构，国内外学者进行了拓扑优化研究。马强[9]开发了一种变密度法程序以优化板/壳结构的加强筋布局。崔荣华[2]应用水平集方法和可移动变形组件法优化了加强筋布局。季金[10]利用改进的自适应成长技术进行了结构柔度和自振频率目标下的加强筋分布优化设计。CHENG等[11]应用渐进均匀化方法和梯度搜索算法研究了受面外屈曲约束的加筋板双尺度概念设计问题。TOWNSEND等[12]开发了一种水平集方法，在考虑线性屈曲的影响下对加筋板进行拓扑优化设计。因高效、实用性强、收敛性好等特点，固体各向同性材料惩罚(solid isotropic material with penalization，SIMP)法已成为工业界和学术界中应用最广泛且最成功的的拓扑优化技术[13]。WARWICK等[14]、ZHAO等[15]应用SIMP内核下的商业优化软件对三维实体单元加筋板结构进行拓扑优化设计，充分验证了SIMP技术应用于加筋板概念设计的可行性。但采用三维实体单元进行加筋板设计存在加强筋-面板断连及计算效率低的劣势[16-19]。此外，在传统SIMP法(conventional SIMP，C-SIMP)中，惩罚因子在拓扑优化迭代过程中为固定值，材料单元密度被过度惩罚，将凸优化问题转换为非凸优化问题，从而迭代收敛至结构局部最优解。另外，鲜有学者对大跨度无支撑甲板进行工程性能拓扑优化研究和进一步的详细设计。

本文基于密度约束准则并应用域偏置手段，实现大跨度无支撑甲板设计域的降维处理。首次将延拓技术引入加筋板概念设计阶段，提出兼顾迭代效率和逼近全局最优解的三段式延拓(three-stage continuation，TSC)法，以处理大跨度甲板刚度、变形及动态振动性能拓扑优化问题。尺寸/材料一体化优化方法联合自动化技术则被应用于大跨度甲板拓扑结构的详细设计。

1 三段式延拓法

本文以SIMP插值技术为理论支撑，其函数为

(1)

式中，xe为单元密度；p为材料惩罚因子；ke为单元刚度矩阵；K(x)为惩罚后的结构整体刚度矩阵。

为缓解惩罚因子过度应用引起的局部最优解问题，延拓法应运而生[20]，并被建议为结构拓扑优化的标准程序[21]。为兼顾迭代效率与全局最优解，本文提出一种TSC法。

阶段一：初始化惩罚因子p1=1，拓扑迭代收敛至灰度设计(低密度单元占大比例)。

阶段二：惩罚因子值p2=p1+1，并以阶段一的灰度设计为起始点，迭代收敛至包含部分中间密度单元的拓扑设计。

阶段三：以阶段二的拓扑设计为初始参考，惩罚因子值p3=p2+1，拓扑收敛至布局清晰的0-1概念设计。

可看出，此TSC法以求解凸优化问题为起始点，且在阶段收敛处，惩罚因子值增加1，可提高获取全局最优解的概率。技术路线图见图1。其中，x0代表初始加强筋单元密度向量；xk为第k阶段的加强筋单元密度向量。因设计变量数量远多于约束条件数量，故采用伴随变量法(adjoint variable method，AVM)高效地进行目标函数灵敏度分析[22]。最后，利用灵敏度信息对有限元模型进行显式近似并基于对偶算法[23]优化加强筋单元密度。

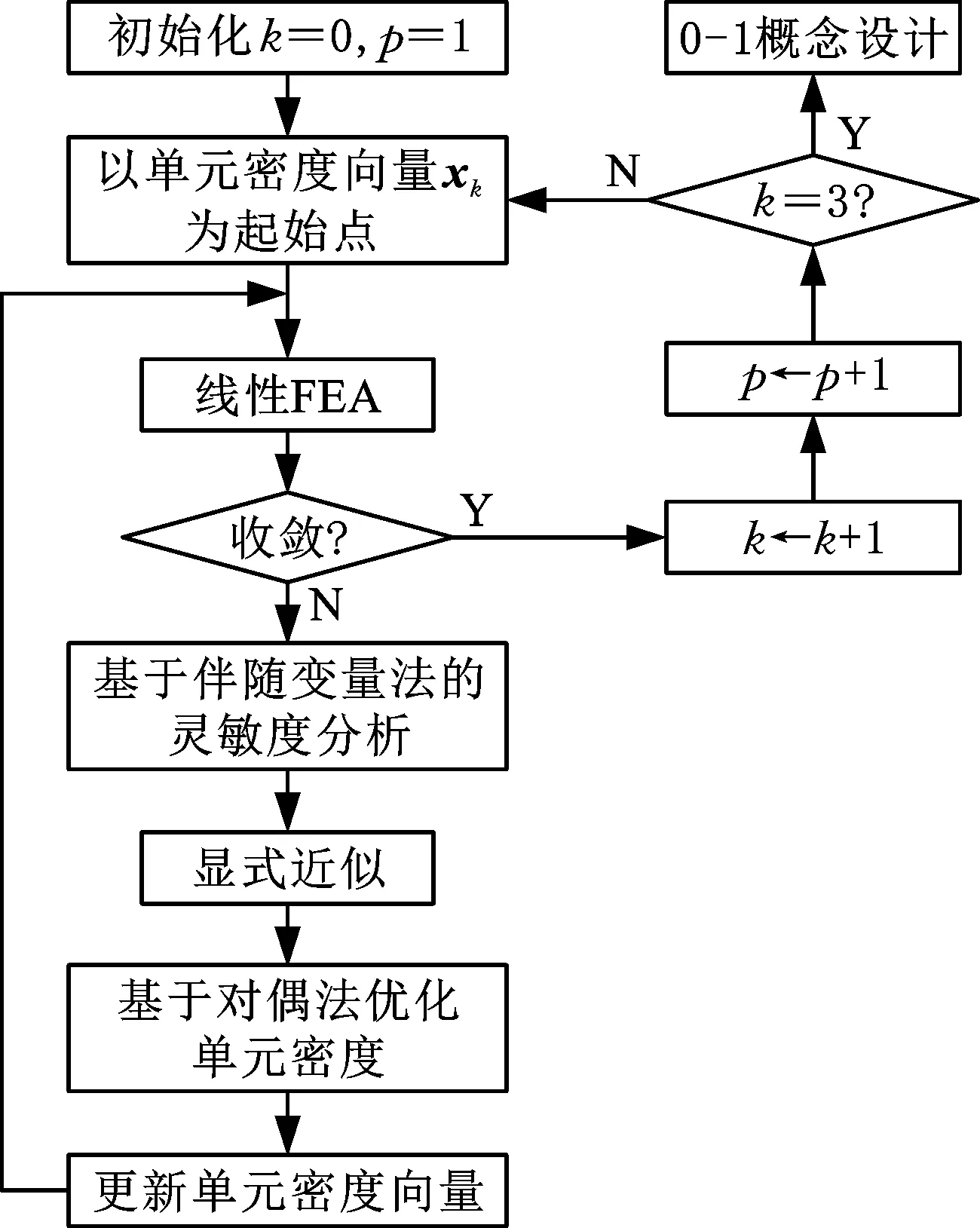
图1 三段式延拓法流程示意图

2 降维处理策略

结构拓扑优化过程中，TSC法借助惩罚因子消除非必要材料以生成“0-1”分布，本质上属于减法模式。如图2所示，基于此原理，加筋板结构拓扑优化技术的思路[14-15]为：①给定加筋板三维设计区域并划分设计域(加强筋域)和非设计域(面板域)(图2a)；②将加筋板设计区域有限元离散为三维实体单元(图2b)；③在TSC法驱动下，消除设计域中的非必要加强筋材料以生成加强筋拓扑布局(图2c)。但上述思路存在两个问题：①加筋板完整性不足，即加强筋-面板存在断连现象，此部分加强筋材料未起到抗弯作用，导致加强筋布局非最优；②大跨度无支撑甲板三维实体单元数量大，其计算效率极低。上述问题可通过如下步骤解决(图3)：①对图2b的z向加强筋实体单元施加密度约束(如拔模约束、挤压约束、铸造约束等)，将z向加强筋实体单元密度均一化(图3a)；②从拓扑优化单元密度角度出发，密度均一化的z向加强筋实体单元即可采用板单元代替(图3b)，实现了加强筋单元的降维处理；③基于TSC法实现加强筋拓扑分布，此时任意加强筋构件均与面板相连(图3c)。板单元的应用同时解决了计算效率低的问题。该策略已被DUGRE等[24]证明有效，但他们采用的同心加筋板结构并不符合工程实际，本文运用域偏置手段(图4)对其进行改进以生成符合工程实际的偏心加筋板布局分布。

(a)3D设计区域 (b)3D有限元模型 (c)3D拓扑结构

(a)均一化密度 (b)2D板单元模型 (c)2D加强筋拓扑布局

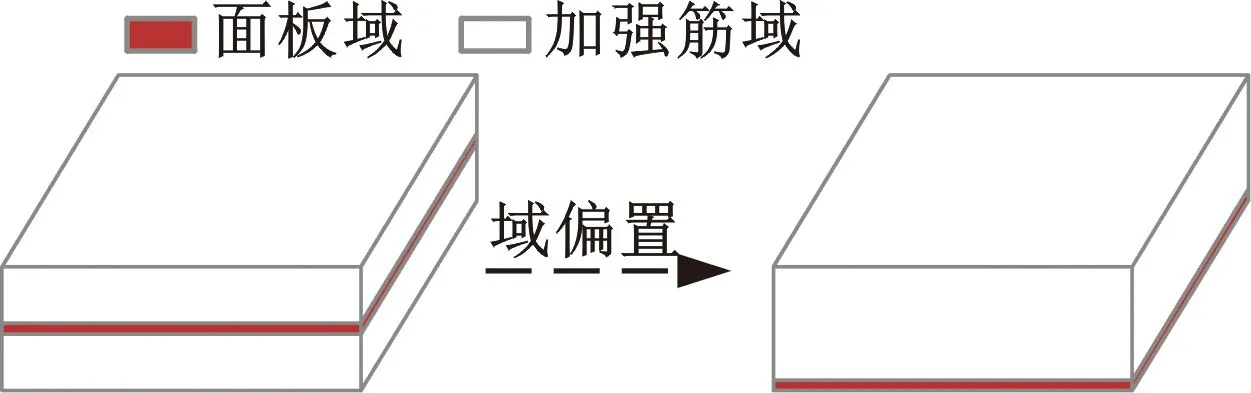
图4 域偏置

3 自动化技术

加筋板设计时，重复人工操作费时费力且易产生人为错误，故引入流程自动化技术以提高分析效率与准确性并降低时间及人力成本，如图5所示。

图5 加筋板拓扑优化流程自动化技术路线图

本文开发了一种通用且高效的流程自动化技术[25]。①前处理(HyperMesh)自动化基本思路为：基于Command文件提取命令函数以实现拓扑优化参数的自动化建立；②应用TSC法并依托OptiStruct求解器实现大跨度甲板的概念-详细设计，通过修改运行选项(采用in-core内存管理模式并设置CPU核数)以硬件加速方式进行计算性能调优来提高计算效率；③后处理(HyperView)自动化则依托于函数结构树，需按照函数结构树提取对象的句柄来实现软件自动化操作，其一般语法格式为

{parent_object_handle_name} {command}

{object_handle_name}

(2)

其中，parent_object_handle_name为父级句柄名称；command为获取子级句柄名称的命令；object_handle_name为子级句柄名称。

此技术兼具可行性与高效性，可推广至其他基于上述软件开展的拓扑优化研究。

4 加筋板算例验证

应用自动化技术，以480个加筋板刚度最大化概念设计算例验证TSC法的有效性。

4.1 拓扑参数设定

加筋板受大小为1的面外均压。四边简支。弹性模量E=2.06×105，泊松比ν=0.3。加筋板网格采用一阶四节点壳单元，大小为1×1。材料体积分数V=0.3，0.4，0.5。目标函数容差ω0=0.0001，以保证拓扑迭代收敛且生成0-1分布的清晰加强筋布局。最小成员尺寸为3倍网格单元大小，用来惩罚小于此直径大小的构件以便于后续工程制造，同时避免了棋盘格现象及网格依赖性问题[26]。C-SIMP法的惩罚因子取值为3[27]，TSC法的惩罚因子初始取值为1。

4.2 算例组

自动化技术支持下(图5)，基于TSC法和C-SIMP法对两组加筋板进行刚度性能最大化概念设计，具体参数如表1所示。面板厚度最小值hmin=0.002，以保证拓扑迭代过程中加筋板受完整面压；面板厚度最大值hmax=HV；面板厚度增量Δh=0.2(此增量由第二厚度点开始)。此外，将B视为基本参数，相同L/B、H/B、h/B下，加强筋刚度设计相同，即本文所研究的加筋板设计具备一定通用性，可为相关设计人员提供一定参考。

表1 加筋板算例组

4.3 结果分析与讨论

图6、图7分别为两组加筋板的拓扑应变能对比图，其中，各分图最左边的为整体对比图；中间的为局部放大图，以实心圆点为对应；最右边的为TSC法相比C-SIMP法拓扑应变能的下降度，即er=(SC-SIMP-STSC)/STSC，其结束点对应局部放大图中的灰色实心圆点。据图6和图7，C-SIMP法下，拓扑应变能随面板厚度增大而呈现四阶段变化，即降低—平缓振荡式增大—大幅振荡式增大—大幅振荡式降低；而TSC法下，拓扑应变能则仅呈现两阶段变化，即降低—指数式平缓振荡增大。基于TSC法的240例加筋板模型的拓扑应变能均低于C-SIMP法，具体下降度如表2所示。其中，拓扑应变能下降度超5%的占比97.5%；下降度超10%的占比86.7%；下降度超20%的占比69.2%；下降度超50%的占比50.4%。表3和表4所示分别为组别一和组别二的最佳面板厚度及相应拓扑应变能。TSC法下，加筋板最优拓扑应变能均下降超4%，充分说明了TSC法在加筋板刚度性能寻优方面的有效性。

(a)V=0.3

(a)V=0.3

表2 TSC法较C-SIMP法的拓扑应变能下降度

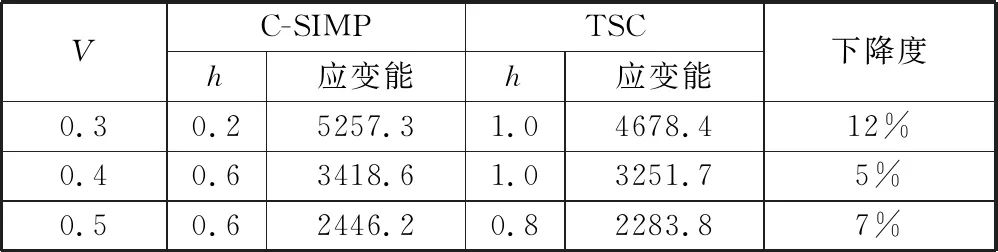
表3 组别一的最佳面板厚度及拓扑应变能对比

表4 组别二的最佳面板厚度及拓扑应变能对比

图8和图9所示分别为组别一和组别二的最佳拓扑布局分布。与C-SIMP法相比，TSC法下的加强筋次要构件(细小构件)减少而主要构件数量更多且分布均匀。

(a)C-SIMP法

(a)C-SIMP法

5 拓扑-尺寸-材料联合优化设计

5.1 大跨度无支撑甲板基准模型

如图10所示，某大跨度甲板[1]长38.4 m，宽22.4 m，面板厚度为14 mm；横梁采用T 750×10/250×20，横向跨度为5.6 m，纵向跨度为2.4 m；纵骨应用HP 220×10，跨距0.7 m。有限元分析中，面板采用二维四节点壳单元模拟，单元数量为86 016；横梁及纵骨均采用一维梁单元模拟，单元数量为15264。大跨度甲板材料属性为E=70 GPa，ν=0.3；边界条件为

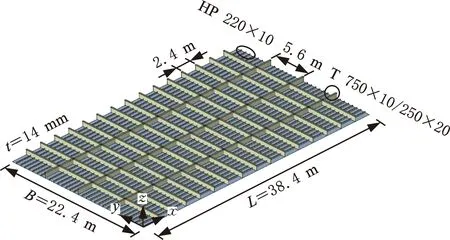
图10 大跨度甲板基准模型

(3)

5.2 工况条件

大跨度无支撑甲板服役工作期间有甲板上浪、船体梁总纵弯曲等工况，本文主要考虑上述两种载荷(图11)。①LC1：甲板上浪产生的均匀面外载荷，p=3 kPa；②LC2：船体梁总纵弯曲产生的面内纵向压力，σ=1.6 MPa。

(a)LC1

5.3 拓扑优化设计

5.3.1拓扑参数

大跨度甲板拓扑优化设计区域依据基准模型空间域确定，总尺寸为38.4 m×22.4 m×784 mm，其中设计域(加强筋域)为38.4 m×22.4 m×770 mm，非设计域(面板域)为38.4 m×22.4 m×14 mm。目标函数容差ω0、最小成员尺寸及惩罚因子设定同上。

对大跨度无支撑甲板基准模型开展静态有限元分析及动态特征值分析以获取概念设计所需的刚度、变形及动态振动指标，具体如表5所示。基于此，构造大跨度无支撑甲板拓扑优化数学模型：

表5 大跨度甲板拓扑优化性能指标

(4)

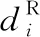
5.3.2大跨度无支撑甲板拓扑结构

三段式延拓法驱动下，无效加强筋材料被“惩罚”，中高密度材料被保留并形成轮廓清晰的加强筋拓扑布局，如图12所示。相较于传统加强筋的密集横纵式正交布局[28]，大跨度甲板概念设计具有构件数量少、构件分布间距大及曲形等特性，可为设计人员提供加筋板前期设计的新思路。

图12 大跨度甲板概念设计结果

5.4 曲形大跨度甲板尺寸/材料一体化优化设计

为便于工程制造与生产，对大跨度甲板概念设计开展尺寸/材料一体化优化设计。概念设计解释策略为：基于大跨度甲板拓扑结构的中高密度材料构造加强筋轮廓线，而后在加强筋轮廓中线位置并沿长度方向布置曲形加强筋基线，如图13所示。曲形加强筋采用T形梁单元模拟，面板则采用二维四节点壳单元模拟。为最大限度提高大跨度无支撑甲板的刚度、变形及振动特性，优化设计变量包含面板及加强筋材料的弹性模量E、面板厚度h及T形梁截面尺寸(图14)。弹性模量E的初始值为70 GPa，面板厚度h的初始值为14 mm。概念设计中，不同位置处的拓扑加强筋宽度不同，为充分体现此特征，采用多类别加强筋设计变量，共44种(图15)。其中，每种加强筋设计变量包含4个子设计变量(图14)。各类别加强筋截面尺寸初始值为：D1=250 mm，D2=670 mm，D3=20 mm，D4=10 mm。179种设计变量的人工建立费时费力且易出现人为失误，故应用命令函数进行高效且准确的自动化建立。

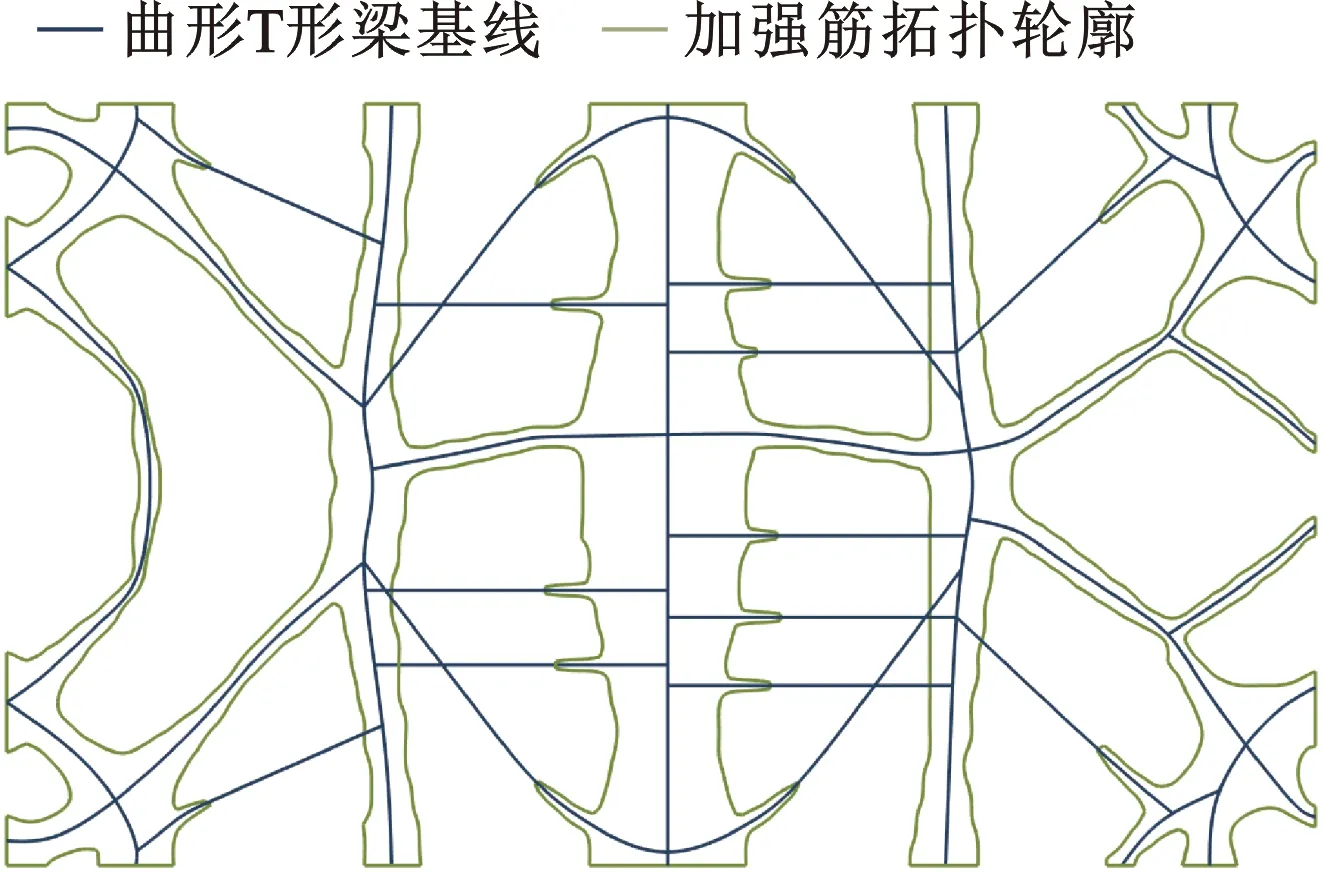
图13 曲形T形梁基线

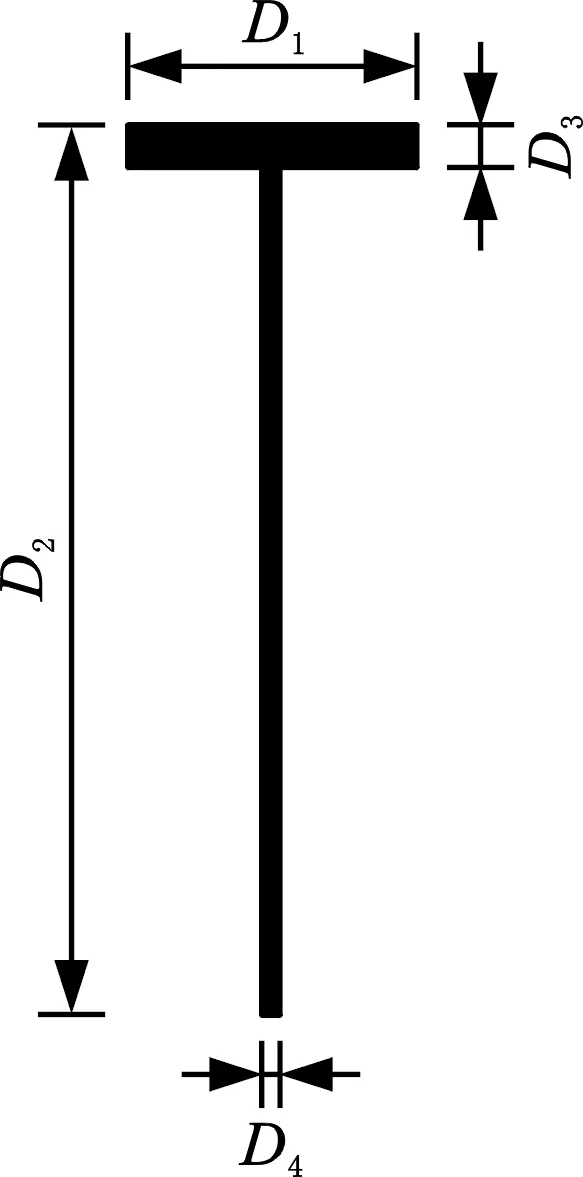
图14 T形梁子设计变量

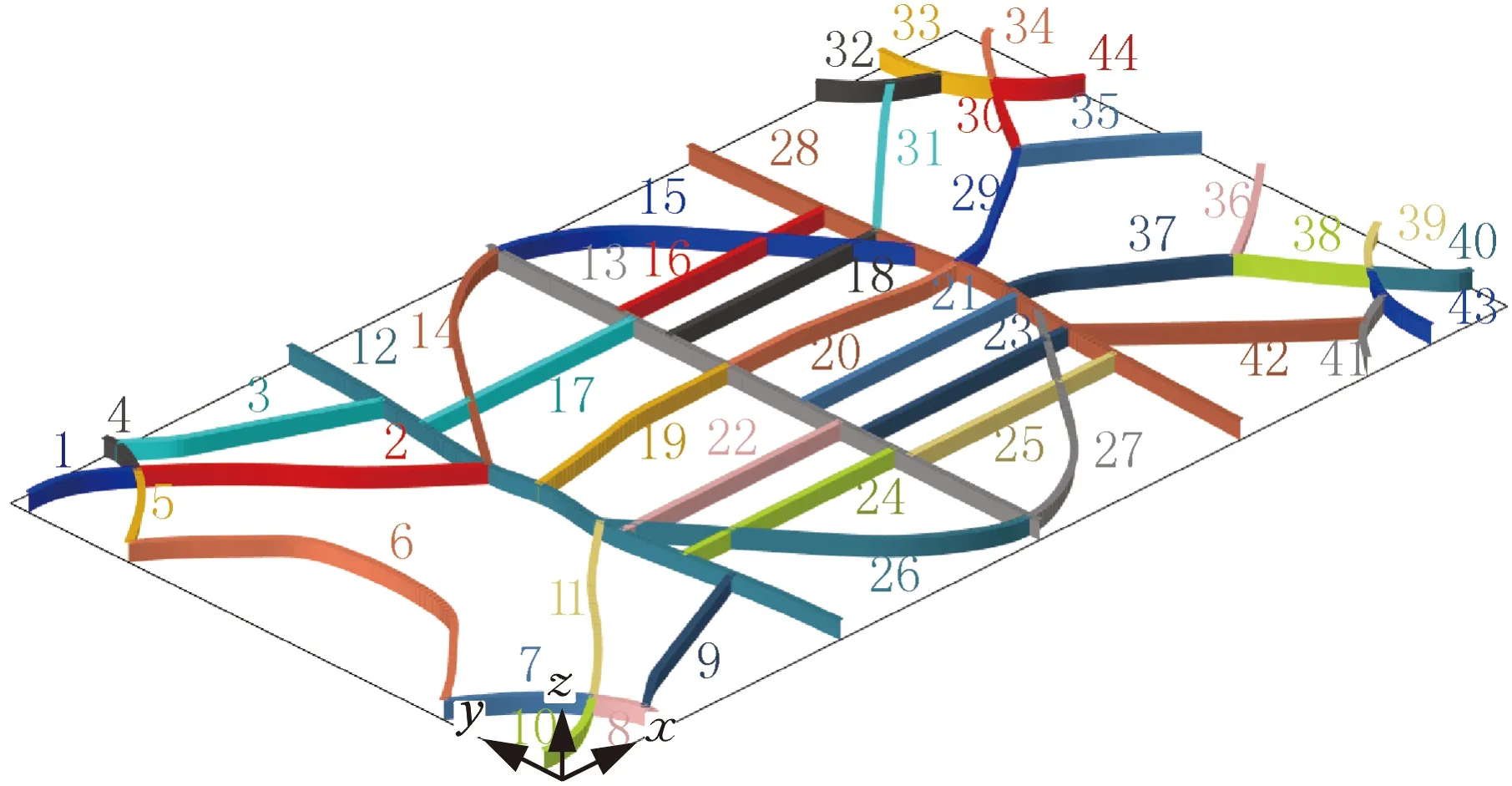
图15 曲形T形梁设计变量类别

大跨度甲板详细设计对标基准模型的刚度、变形及动态振动性能，基于此，构建大跨度无支撑甲板尺寸/材料一体化优化数学模型：

(5)

式中，E1为加强筋弹性模量；E2为面板弹性模量；D1，k～D4，k为第k种加强筋类别的截面尺寸变量。

历经184步，大跨度无支撑甲板尺寸/材料优化迭代收敛，如图16所示。迭代初，甲板材料的弹性模量较小，为满足性能需求并降低最大约束违反，大跨度甲板新设计总体积增大；而后，最大约束违反降为0，并随弹性模量增大，总体积呈减小趋势；迭代至144步，大跨度甲板新设计总体积降至20.49 m3，略小于基准模型总体积(20.54 m3)，此时加强筋及面板材料的弹性模量均增至293 GPa。迭代收敛时，加强筋及面板材料的弹性模量均增大至上限值，即E=420 GPa，而大跨度甲板新设计的总体积VT=17.25 m3。可知，材料弹性模量的增大，对降低大跨度甲板成本并提高其刚度、变形及振动性能具有重要作用。

图16 尺寸优化迭代历史

大跨度无支撑甲板多应用于空间资源稀缺的滚装船、油船、舰船及航母等大型装备，在保证甲板性能的基础上减小材料总体积具备工程实际意义，故第144～184步的尺寸/材料优化设计结果均可被应用，但弹性模量愈大，甲板材料要求也愈高，故第144步下的大跨度甲板新设计被最终采用。值得注意的是，E=293 GPa的材料弹性模量已高于钢材弹性模量，甲板选材应为高刚度复合材料。该迭代步下的面板厚度h由14 mm增加至19.43 mm。曲形T形梁截面尺寸优化值如表6所示。曲形大跨度无支撑甲板新设计如图17所示。

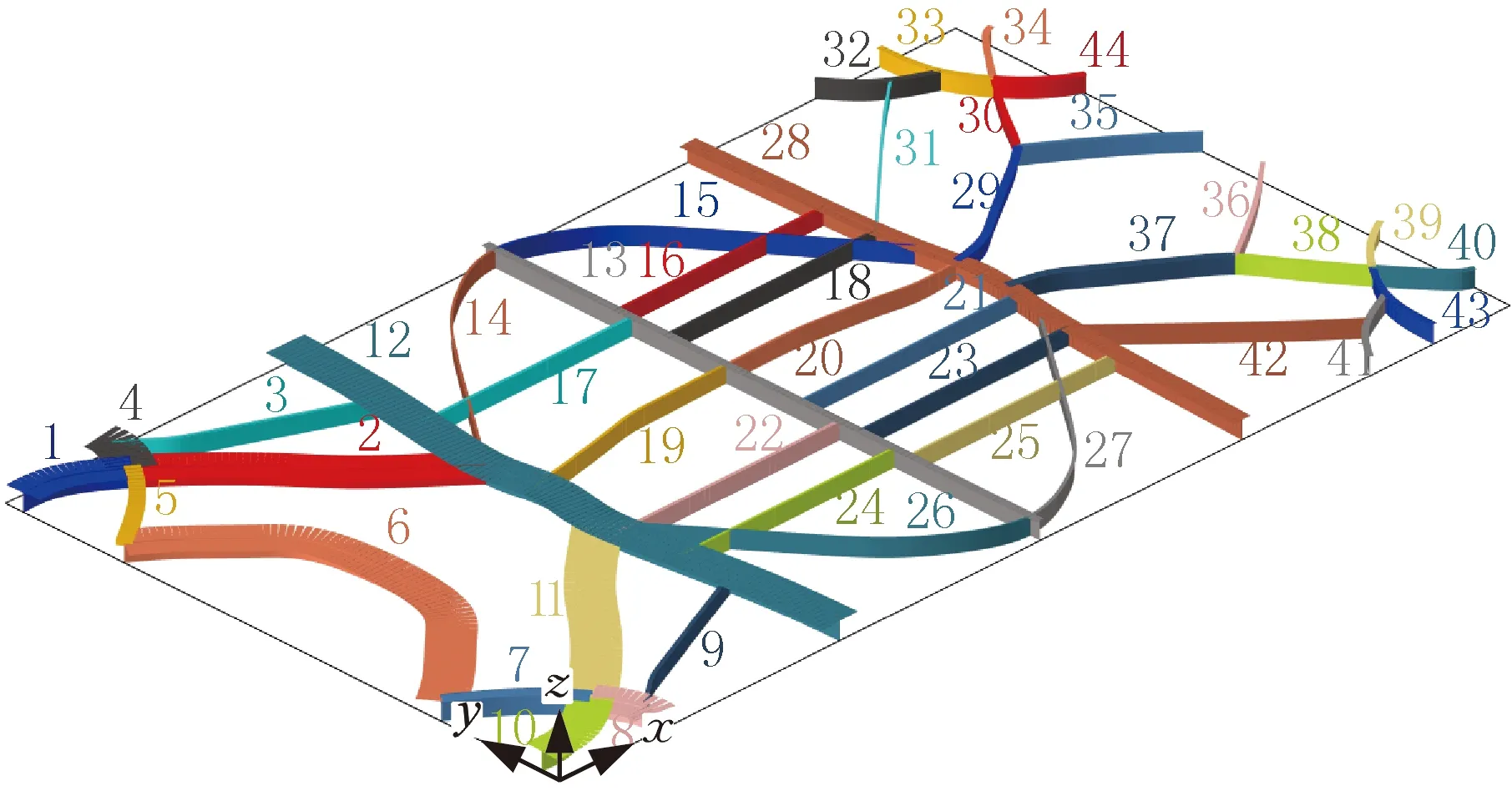
图17 曲形大跨度甲板新设计

表6 T形梁截面尺寸优化值

从空间角度出发，大跨度无支撑甲板基准模型总体积为20.54 m3，T形梁总高度为770 mm；而曲形大跨度甲板新设计的总体积VT=20.49 m3，仅5号和7号T形梁高度为760 mm，其余T形梁高度均低于670 mm。可知，在大跨度甲板总体积略减小的基础上，可节省13%的高度空间。此外，分布较为离散的加强筋布局可为船体线缆布置提供充足空间。

表7所示为曲形大跨度甲板新设计与基准模型的性能对比。从性能角度出发，曲形大跨度甲板新设计的应变能分别降低10.21%、15.43%，其刚度性能得到有效提高。工况LC2下的甲板最大节点位移下降61.46%。一阶动态特征频率由2.52 Hz升至2.76 Hz，提高9.52%。相较于传统加筋板布局，曲形大跨度无支撑甲板新设计具备空间及性能双重优势，证明了概念设计解释策略及尺寸/材料一体化设计方法的先进性。此外，概念设计为详细设计提供曲形T形梁位置支持，进一步证明了降维处理策略及TSC法组合应用于大跨度甲板概念设计的有效性。

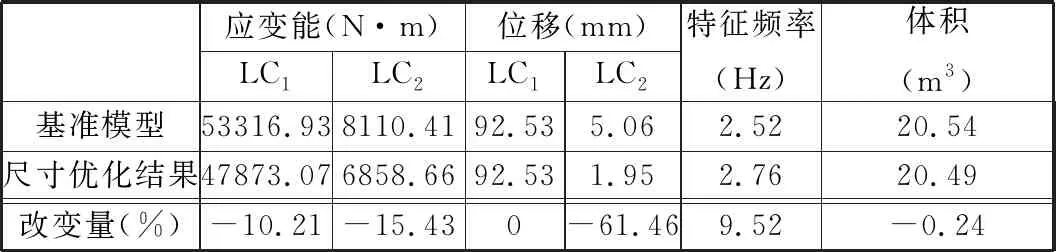
表7 曲形大跨度甲板新设计与基准模型性能对比结果

6 结论

基于降维处理策略和三段式延拓(TSC)法对大跨度无支撑甲板开展应变能、多工况位移及动态频率性能拓扑优化设计。应用尺寸/材料一体化设计方法并联合自动化技术对大跨度甲板拓扑结构进行详细设计以便工程制造。自动化技术下的480个简单加筋板算例证明TSC法具备更优的拓扑刚度性能和更广的面板厚度适用性。与常规大跨度甲板相比，TSC法下的大跨度甲板概念设计具有构件数量少、构件分布间距大及曲形等特征，可为设计人员提供加筋板前期设计的新思路。此外，曲形大跨度甲板新设计的总体积略减小，并可节省13%的高度空间。刚度性能最高提高15.43%，最大变形至高降低61.46%，一阶振动特性提高9.52%。进一步说明了降维处理策略和TSC法应用于大跨度加筋板概念设计的先进性。