考虑二次衬砌有效承载厚度的隧道结构安全系数解析模型
刘新荣,周伟锋,周小涵, *,庄 炀,王自强
(1.重庆大学土木工程学院,重庆 400045;2.库区环境地质灾害防治国家地方联合工程研究中心,重庆 400045;3.山地城镇建设与新技术教育部重点实验室,重庆 400045)
0 引言
截至2021年,我国交通隧道已达到40 800处,累计里程4 575.39万延米[1-2]。随着交通网络的饱和,大规模的隧道建设期将逐渐过渡到长时间的运营维护期。隧道施工过程中出现的地层欠挖、围岩大变形、模板变形漏浆等问题导致的衬砌混凝土浇筑不到位,以及运营过程中遭受硫酸盐等物质的侵蚀引起的混凝土剥落、强度丧失等问题,均会致使二次衬砌厚度损失[3-4],从而削弱衬砌刚度,产生较大变形,侵占行车空间,甚至出现二次衬砌断裂引发塌方的情况,危及行车安全[5-6]。因此,在二次衬砌厚度损失的条件下,判断运营隧道的安全状态具有重要的现实意义。
目前,对于二次衬砌厚度损失条件下隧道安全状态的判断研究主要基于数学评价模型和数值分析模型。采用数学评价模型需要收集大量工程案例建立数据库[7-8]或者依赖人为经验评价判断[9-10],并且隧道实际的安全状态无法准确获知。通过有限元、离散元等建立的数值模型[11-12],虽然能准确地模拟衬砌的力学特征,但是数值软件的学习、精细化模型的建立、本构模型参数的选定以及计算过程需要占用大量的时间与资源,因此制约了其在工程中的推广应用。此外,简化力学模型[13-14]也常用于隧道的受力分析,虽然计算精确度较数值模型差,但是由于其难度小、计算速度快等,目前被工程人员广泛应用。弹性地基梁模型作为一种简化力学模型,能够较好地反映地层对衬砌的弹性抗力作用,因此使用频率较高。目前,弹性地基梁法大多采用直梁单元迭代求解,但单元尺寸划分对结果的真实性影响较大[15]。因此,也有部分学者采用弹性曲梁的方式进行衬砌力学分析[16-19]。分析认为,衬砌承受的荷载等于土弹簧压力,通过假定初始参数进行迭代求解,最后借助现场监测数据并结合对称性确定初始参数。Wang等[20]、黄伟明等[21]采用空间状态法将内力与位移对偶进行盾构隧道管片受力分析,分开考虑土弹簧与地层荷载,虽然回避了确定待定参数,但是在求解荷载项时形成了复杂的荷载积分,导致最终解析公式复杂。剧仲林[22]结合圆曲梁和弹性地基曲梁理论求解初期支护拱部的内力和位移,但由于确定待定参数时采用与求解过程不一致的两脚拱模型,导致结果可能存在误差。综上所述,目前弹性地基梁理论的发展已经较为成熟,但是待定参数的确定依然值得进一步研究。同时,该理论在二次衬砌厚度损失条件下隧道安全评估方面的应用研究较少。
鉴于此,本文基于弹性地基曲梁理论,根据空间状态法建立衬砌力学响应解析解模型,采用Laplace变换进行模型解析,并与数值模型计算结果进行对比验证。本文提出的解析解形式简洁,避免了求解过程中出现复杂的荷载项解析公式,依靠基本地勘资料即可进行计算。
1 模型建立及基本假定
隧道开挖后,围岩往往产生较大的变形,使得围岩-衬砌能够紧密贴合,因此可以将衬砌近似看作是支承在弹性地基上的曲梁。由于衬砌结构厚度的损失,隧道截面由等厚的均质环逐渐演变为齿状的阶梯形连续曲梁。因此,其力学模型可以近似地考虑为弹性地基上的阶梯形曲梁,如图1所示。根据二次衬砌的几何曲率,荷载形式,厚度损失范围、程度、位置,将二次衬砌分为n段,记为L1,L2,…,Ln。其中,未劣化时的二次衬砌设计厚度为h0,损失厚度为ci,任意一段二次衬砌的有效承载厚度为h0-ci,半径为Ri,厚度损失范围为di。

图1 二次衬砌厚度损失模型
基于以上条件,做出如下假设:1)围岩满足Winkler弹性地基梁模型;2)二次衬砌可以视为欧拉曲梁,符合平截面假定,衬砌材料满足线弹性要求;3)忽略由于截面突变导致形心轴偏移的误差。
2 弹性地基曲梁模型解析
2.1 弹性地基上的曲梁单元
从厚度劣化的二次衬砌结构上取出一段微元体Rdθ,其受力情况如图2所示。建立局部坐标系,其中,ρ和φ分别代表径向和切向,对应方向的位移为uρ和uφ,截面面积为A,惯性矩为I,中性面的半径为R,截面弯矩为M,剪力为Q,轴力为N,弹簧径向和切向抗力系数分别为kρ和kφ,作用在微元体上的径向压力为qρ,切向压力为qφ。各物理量的正向如图2所示。

图2 弹性地基曲梁微元受力示意图
根据弹性力学可知,切向位移和径向位移均可以导致曲梁产生转角和切向应变。由此可知,曲梁转角γ和中曲面处的切向应变εφ分别为
(1)
(2)
由假定3)可知,轴向应力在截面高度上满足线性分布,截面的平均应力应等于中曲面处的轴向应力。此外,衬砌材料为线弹性材料,满足胡克定律。因此,截面轴力
(3)
式中E为二次衬砌材料弹性横量。
弯矩和轴力均会导致微元体的转角改变,其中,弯矩增大,微元体的转角增大(转角与弯矩正方向相同),而轴力增大,微元体转角减小。根据材料力学可知,弯矩和轴力对转角的改变量分别为式(4)中等式右侧的第1项和第2项。
(4)
由于h≪R,可以近似地认为外周半径等于中性轴半径R。则根据图2得到的微元体受力平衡方程,同时略去高阶微量后可以得到如下方程:
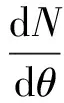
(5)

(6)

(7)
通常在衬砌受力分析中,衬砌压力通过直角坐标系以水平压力qx与竖直压力qy的形式给出,而qφ和qρ是极坐标形式,则根据坐标变换公式得出
式中qx与qy分别代表衬砌所受水平压力与竖直压力的绝对值。
2.2 弹性地基上曲梁单元解析矩阵
采用空间状态法,将内力与位移对偶[21],将式(1)和式(3)—(6)整理为一阶方程矩阵形式,见式(8)。

(8)
式中:S为力学响应矩阵;D为系数矩阵;f为衬砌承受的外荷载矩阵。
对式(8)两端进行Laplace变换,可以得到
Y(s)=(Is-D)-1S(0)+(Is-D)-1T(s)。
(9)
式中:S(0)为力学响应矩阵的始端状态物理量;Y(s)和T(s)分别为S和f的象函数;I为6阶单位矩阵;s为θ的映射变量。
对式(9)做Laplace逆变换,即可求得力学响应矩阵S的解析式:
S(θ)=L-1[(Is-D)-1]S(0)+L-1[(Is-D)-1T(θ)]。
(10)
式中L-1为Laplace 逆变换符号。
令
(11)
(12)
则
(13)
2.3 弹性地基上考虑厚度损失的衬砌环内力与变形
衬砌环由L1~Ln段彼此刚性连接构成,接头处内力与位移连续变化。对于梁Li,其始端记为Li,0,终端记为Li,1,因此二次衬砌变形、内力在曲梁间的传递方程为
Si,0=Si-1,1。
(14)
式中:Si, 0为第i段曲梁始端力学响应矩阵;Si-1, 1为第i-1段曲梁终端力学响应矩阵。
由2.1节可知,变形、内力在曲梁Li内的传递方程为
(15)
联立式(14)和式(15),计算得到二次衬砌任意截面的变形与内力:
(16)
解析式(16)中第1段曲梁初始力学响应矩阵S1, 0含有6个内力与位移待定参数需要求解。考虑到二次衬砌作为一个封闭的环状结构,虽然被离散为n段曲梁,但实质上首尾相接、协调变形,第n段曲梁终端的内力、变形应等于第1段曲梁始端的内力与变形,即
Sn,1=S1,0。
(17)
将式(16)代入式(17)可解出S1,0。
(18)
将式(18)回代入式(16)中,可以得到二次衬砌任意截面处的内力和变形。
3 解析解验证
为验证解析解的可靠性,本文以某Ⅳ级围岩深埋公路隧道为工程背景,采用数值软件(ANSYS)对衬砌的内力和位移进行模拟。采用数值软件建立的荷载-结构模型如图3所示。其中,隧道断面采用《公路隧道设计规范》[23]中的三心圆断面,二次衬砌为45 cm厚的C25混凝土,弹性模量为28 GPa。隧道顶部承受垂直均布压力qy=115.72 kPa。由于隧道埋深较大,将侧向梯形水平荷载简化为均布水平荷载qx=34.72 kPa。参考《公路隧道设计细则》[24]中地基弹簧抗力系数的取值,径向弹簧的抗力系数为kρ=400 MPa/m。切向弹簧抗力系数分别取kφ=0[24]和kφ=kρ/3[25]。通过自行设计Matlab代码对衬彻的内力和位移进行求解,试算1~2次后确定顶部弹簧受拉区,受拉区内弹簧刚度归零。

图3 荷载-结构模型(单位:cm)[23]
图4示出在kφ=0和kφ=kρ/3 工况下,轴力与弯矩的解析解与ANSYS数值解的对比结果(θ=0°~180°)。可以看出,采用2种方法所得结果的吻合度较高。当kφ=0时,随着θ的增大,轴力总体呈现增大趋势,而弯矩呈现波浪形变化。其中,拱顶位置承受最大正弯矩94.4 kN·m,在拱腰(θ=50°附近)和拱脚(θ=125°附近)位置出现负弯矩的极大值。衬砌作为典型的偏心受压构件,截面承载能力受到弯矩和轴力耦合作用的影响。因此,可以认为拱顶、拱腰、拱脚是该衬砌的危险截面。相较于kφ=0,当kφ=kρ/3时,切向弹簧可以分担部分荷载,因此弯矩和轴力曲线较为平缓,同时轴力在弹簧非受拉区逐渐减小。
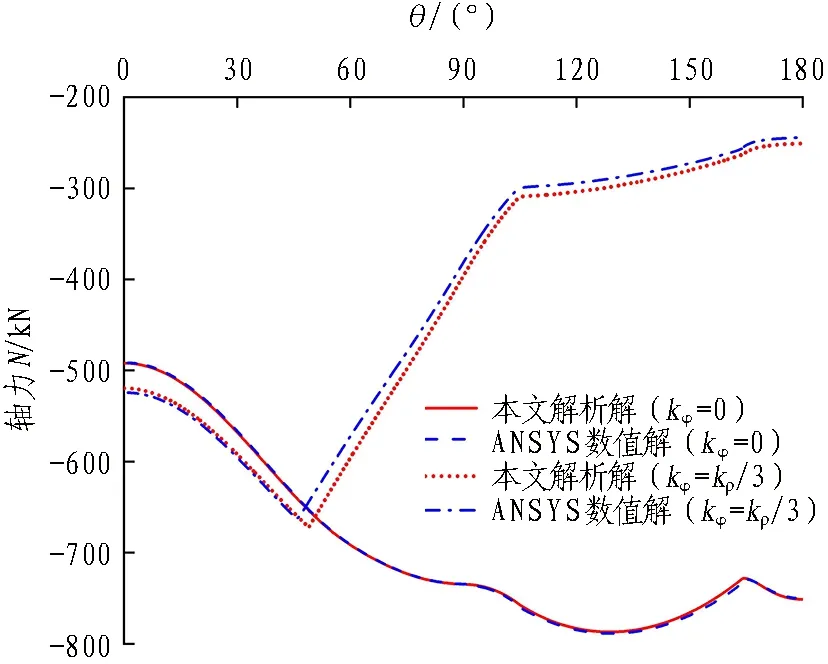
(a)轴力
4 二次衬砌厚度损失下隧道结构的安全性分析
拱顶、拱腰和拱脚作为隧道截面的控制截面,同时也是二次衬砌厚度损失的易发区。针对这3个位置(拱腰、拱脚均取左侧劣化)进行厚度损失范围和损失程度(损失厚度)的计算分析,具体计算工况见表 1。其中,工况1#表示二次衬砌厚度正常的情况(h0=0.45 m);工况2#—6#、7#—11#、12#—16#分别针对拱顶、拱腰、拱脚二次衬砌厚度损失范围的情况;17#—20#、21#—24#、25#—28#分别表示拱顶、拱腰、拱脚二次衬砌损失厚度的情况。计算采用图3所示模型。由于本文主要探讨二次衬砌局部厚度损失情况下隧道结构安全性的变化规律,因此忽略初期支护所分担的部分荷载。此外,考虑到防水板的存在,切向弹簧刚度取为0[23]。
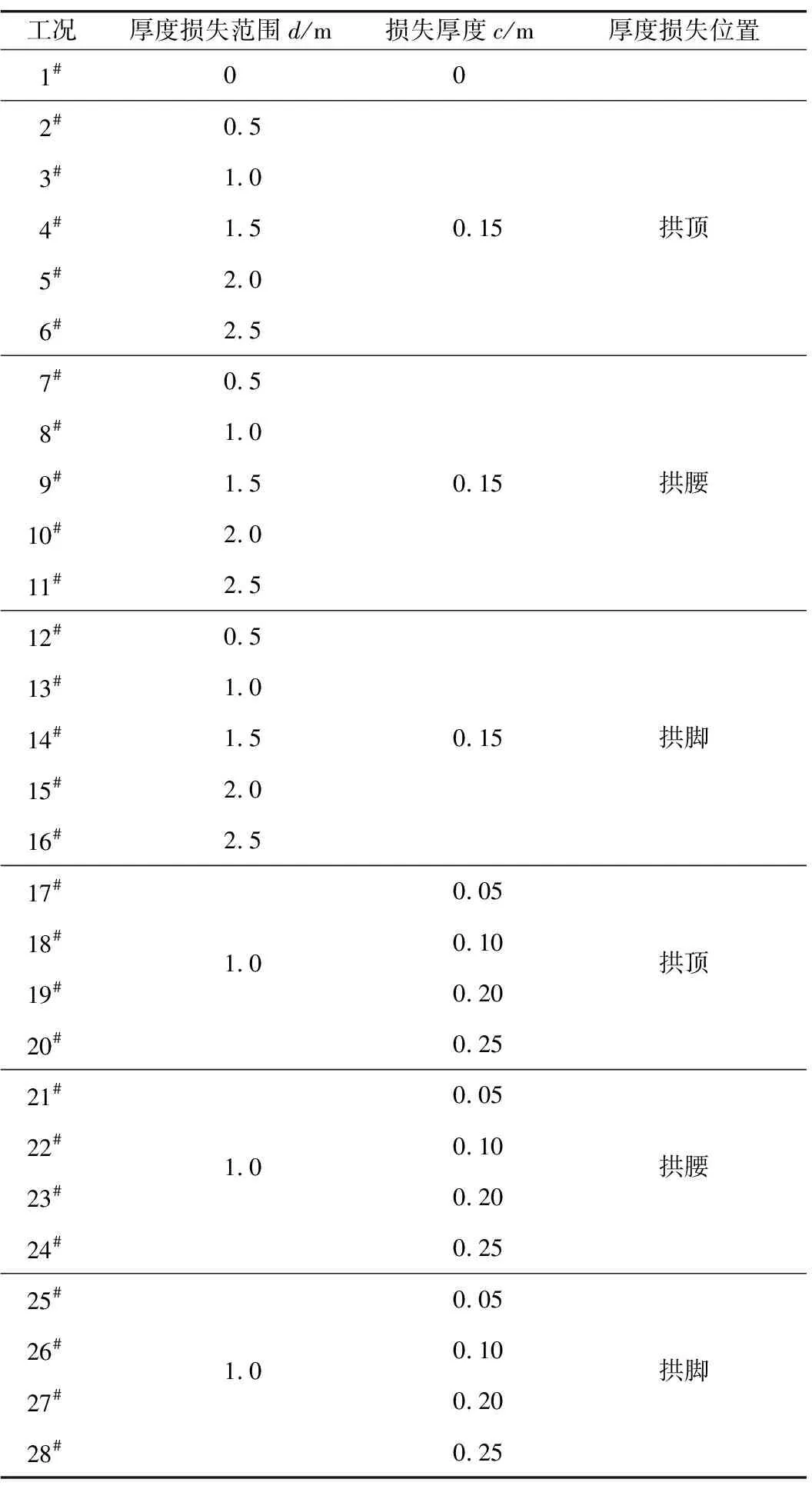
表1 计算工况表
《公路隧道设计规范》[23]规定:混凝土衬砌的安全系数由抗压强度控制时,安全系数的计算公式为
KN≤φαRabh。
(19)
(20)
由抗拉强度控制时,安全系数的计算公式为
(21)
式(19)—(21)中:K为安全系数;φ为构件纵向弯曲系数,对隧道衬砌可取1;α为轴向力的偏心影响系数,可根据经验公式(20)确定;e为偏心距;Ra为混凝土或砌体的抗压极限强度;b为截面宽度;h为截面厚度;Rl为混凝土或砌体的抗拉极限强度。
4.1 二次衬砌厚度损失范围对结构安全性的影响
图5示出拱顶、拱腰和拱脚损失厚度为0.15 m时,二次衬砌各位置安全系数随厚度损失范围d的变化规律。可以看出,拱顶、拱腰和拱脚安全系数呈现相似的变化规律。其中,局部厚度的降低对于远离劣化位置的结构安全系数影响较小,其变化曲线近似于水平线;而厚度劣化位置的安全系数变化曲线类似于“汤匙形”的3阶段变化曲线。3个阶段的变化情况分别为:1)第1阶段,二次衬砌厚度开始出现劣化,该位置的安全系数显著降低;2)第2阶段,随着劣化范围的逐渐增大,二次衬砌安全系数呈现近似线性的回升趋势;3)第3阶段,当劣化范围足够大时,安全系数趋于稳定。
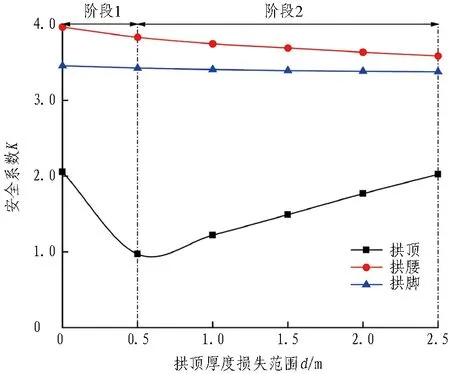
(a)拱顶厚度损失范围的影响
为了探究二次衬砌安全系数随厚度损失范围的变化曲线呈现“汤匙形”的原因,以拱腰(对应工况1#、7#—11#)为例,提取内力进行分析,得到拱腰厚度损失范围对拱腰内力的影响,结果见图6。

图6 拱腰厚度损失范围对拱腰内力的影响
由图6可知:随着拱腰处二次衬砌厚度损失范围的增大,该位置处的轴力几乎无变化,但弯矩呈现下凹式二次抛物线的降低规律;此时,偏心距e(e=M/N)与弯矩同步降低,在截面尺寸不变的情况下,偏心影响程度降低,极限承载力提升,因此,第2阶段的安全系数有所提升。值得注意的是,由于内力的重分布,在厚度损失区域周围的部分非劣化位置,安全系数有一定程度的下降,以θ=20°为例,当厚度损失范围由0.5 m增大到2.0 m时,解析解计算得出的安全系数由13.7降为7.0。而在第1阶段,虽然e有所降低,但二次衬砌截面积相较于工况1#降低了1/3,因此安全系数明显降低;在第3阶段,弯矩变化较小,安全系数也趋于平稳。
4.2 二次衬砌损失厚度对结构安全性的影响
图7示出在拱顶、拱腰、拱脚厚度损失范围为1.0 m时,减小二次衬砌局部厚度对二次衬砌各位置安全系数的影响规律。
由图7可以看出:当二次衬砌厚度局部损失时,在劣化区域内,安全系数呈现先减后增的2阶段变化规律。其中,第1阶段呈现近似线性下降的趋势。而非劣化区的安全系数则由于内力的重分布,存在不同程度的下降。以拱顶厚度损失为例,当c由0增大到0.25 m时,对应拱腰和拱脚安全系数的降幅分别为8.8%(由3.97减小为3.62)和3.1%(由3.46减小为3.35)。
以拱顶为例进行分析(如图7(a)所示),提取对应工况(1#、17#—20#)拱顶处的弯矩和轴力,结果如图8所示。由图8可以看出:随着拱顶厚度的减小,拱顶处轴力仅有5.5%的微小增幅(由491.9 kN增大为518.8 kN),因此可以忽略轴力变化对安全系数的影响;而弯矩呈现上凸形下降曲线,拱顶衬砌厚度越小,弯矩的降幅越大,偏心距e也表现为相似的变化规律。

图8 拱顶损失厚度对内力的影响


图9 相对偏心距η和偏心影响系数β随拱顶损失厚度c的变化曲线
KN≤(1.75βRlb)h。
(22)
由图9可以看出:η和β随c的变化曲线可以近似分为Ⅰ、Ⅱ 2个阶段。其中,第Ⅰ阶段,截面抗弯刚度削减程度不高,劣化段二次衬砌依然是承载的主体,拱顶弯矩M与截面厚度h近似为线性变化,偏心影响系数β较为稳定,如式(22)拱顶安全系数随截面厚度也呈近似线性变化(η和β实际上有所变化);而在第Ⅱ阶段,截面抗弯刚度大幅降低,导致内力重新分布,劣化段内的弯矩和η急剧减小,β陡增,当β对安全系数的增益效果高于h的减小时,安全系数则会增大。然后,通过有限元模型进行了验证分析,发现同样存在安全系数增大的现象。虽然计算所得安全系数偏大,但是由于局部劣化会产生较大变形,对结构稳定性不利,在实际工程中,应同时考虑安全系数与变形的影响。
5 结论与讨论
本文基于弹性地基曲梁理论,根据空间状态法构建衬砌力学响应解析解模型,并采用Laplace变换求解了衬砌各截面的内力与位移,其与有限元数值模型计算结果较为吻合。相较于常规弹性地基曲梁模型,本文构建的解析解模型考虑了地层荷载和围岩抗力的作用,无需通过现场监测数据即可确定初始计算参数,可将其应用于二次衬砌厚度损失条件下隧道安全状态评估中。主要得出以下结论:
1)随着二次衬砌厚度损失范围和程度的增加,劣化位置的轴力无明显变化,而弯矩因刚度的减小而显著降低,偏心距随弯矩同步降低。
2)扩大二次衬砌厚度损失范围,损失区域的弯矩呈下凹式抛物线形降低,截面偏心程度减小,安全系数呈现突降—回升—稳定3阶段的“汤匙形”变化规律;而远离劣化区域的安全系数变化较小。
3)当二次衬砌厚度损失较小时,劣化位置处弯矩与二次衬砌厚度同步降低,轴力偏心变化对安全系数的影响较小,安全系数随二次衬砌有效厚度的变化近似呈线性降低。当二次衬砌厚度损失程度继续增大时,轴力偏心距的降低对安全系数的增益显著提升,大于二次衬砌厚度减小的劣化效应,安全系数反而增大,但是局部可能发生变形破坏。
本文对于厚度损失的二次衬砌安全性的分析主要基于弹性阶段,但实际在衬砌开裂或局部屈服后,仍然具备一定的承载能力,因此对于出现塑性行为的衬砌,其安全状态评估具有重要意义。鉴于此,后续可开展不同损失厚度的衬砌承载模型试验,进一步验证和拓展局部塑性状态下的本文解析解将是以后的主要研究方向。

