磁轮驱动钢罐道巡检机器人研究

封 华，李 强,，陈朋朋

（1. 陕西延长石油矿业有限责任公司，陕西 西安 710075；2. 中国矿业大学 机电工程学院，江苏 徐州 221116）

0 引 言

随着现代工业的全面智能化发展，以机器人代替人工作业已经成为各个行业的必然趋势。一些环境恶劣、工作时间长、距离跨度大等的作业场景，尤其需要机器人技术的引入。矿井提升系统的巡检和维护作业就是典型范例，罐道在提升系统中对提升装备起到导向限位的作用，能有效消除容器在提升过程中产生的水平晃动，使之平稳运行。罐道的表面质量和安装状态是否良好，每段罐道间的间隙和偏角大小都会影响整个导向系统的可靠性，损伤累积逐渐引发故障，导致提升容器的异常振动，影响提升系统的安全运行。

目前罐道检测方法主要有几何测量法、专业仪器法、振动加速度法[1-3]。李占芳等[4]通过建立提升容器振动模型，分阶段对罐道状态进行估测。GALLOWAY等[5]使用了类似的方法，还通过矿井实际试验验证使用效果。蒋玉强等[6]则进一步将钢丝绳模型参数融合进来，对不同振动激励成因进行了详细分析。王东权等[7]借助安装在罐耳上的传感器获得载荷和加速度信号，分析了井筒装备与提升容器之间产生的水平冲击力的影响因素以及作用范围。王鹏等[8-10]也采用了振动加速度数据为主体的罐道性能评价方案。此外，在国外应用振动加速度来检测刚性罐道动态方案也较为常见[11]。传统测量方法存在效率低、流程复杂、精度较差等问题，使用机器人对矿山等工作场所进行巡检已成为必然趋势[12-13]。特殊环境的攀爬作业是移动机器人领域的重要研究方向，把机器人的地面移动方法与垂直表面吸附手段有机结合起来，使得机器人可行驶在不同种类的纵深环境当中，来完成相应任务。

将攀爬移动机器人应用于各个检测领域的尝试已具备一定研究和工作基础。TACHE等[14]设计的一种用于水管检测的五自由度两轮式磁轮机器人，该机器人车体分为两节，车轮前后排布，且各配置一个辅助磁轮，面对交叉壁面具有很好的适应能力，可在内外直角以及阶梯壁面环境工作。EICH等[15]也设计了一种两轮式爬壁机器人，该机器人前部配有2个镶嵌有多个圆柱磁铁的驱动轮，通过差速的形式实现驱动，主要用于船舶表面的检测。该机器人重量轻，但其运动能力不足，仅能完成内角壁面过渡。除了圆轮外，日本的TSUKAGOSHI等[16]研发了一种主动轮为四边形结构的三轮式爬壁机器人，轮子表面使用高黏结性材料来实现吸附，使得运动机器人运动时对表面质量要求较高。SLOCUM等[17]设计的一种三角形结构的爬壁机器人Maggie，以摩擦的方式实现主动轮的转动。该机器人仅能够实现大钝角交叉壁面的跨越，无法实现直角及以内的翻越运动。SCHOENEICH等[18]研究了一种磁吸附履带式爬壁机器人Tripillar，其将磁铁嵌入履带上，通过辅助轮可将履带支撑为三角结构，方便通过内直角环境，但其无法进行外直角的跨越。SEO等[19]设计了一种带传动分体式机器人，由4部分组成。通过铰链板抬高前部车体实现跨壁面运动。该机器人具有良好的移动性能，但其对壁面清洁度要求较高，在粗糙或灰尘较大壁面，易发生下滑或倾覆等危险。杨保强[20]研究设计的一种壁面跨越磁吸附爬壁机器人，其为双体六轮式壁面跨越爬壁机器人，整体为钝角三角形结构，可自主实现内直角壁面跨越。李志海[21]设计的一种轮足混合驱动爬壁机器人，综合了轮式高效移动与足式高效越障的优点，使得机器人能够同时适应铁磁性壁面与地面复杂环境。

综上所述，结合现有的钢结构建筑攀爬技术，针对罐道巡检环境进行分析，设计一种磁轮驱动的钢罐道巡检机器人，该机器人通过永磁轮吸附在罐道表面进行攀爬，借助各个单元之间的万向节连接，机器人可以在罐道各个表面进行翻越，同时也可以攀爬至罐道梁等辅助设施上，借助机器人上搭载的视觉等传感器实现钢罐道的全方位巡检。一方面，该机器人的巡检能力可以解决传统人工巡检的人为误差和检修不完全的问题，另一方面，该机器人可以攀爬至罐道梁等位置进行躲避，使其可以在不停机情况下进行巡检。

1 巡检机器人结构设计

为了对立井钢罐道进行全方位巡检，需要设计一种能在钢性罐道上以低速巡检、高速通过无缺区并且能够自主跨越外直角或其它形状角度（介于180°～270°）交叉壁面、运动性能灵活且易于控制的巡检机器人，为罐道壁面以及井筒周围状态的监测、维护作业工具提供平台支持。

1.1 吸附方式及运动方式

现有研究中攀爬机器人常用的吸附方式主要有负压吸附、磁力吸附以及仿生机械式吸附3种方式，3种类型优缺点见表1。在矿井提升系统以安全生产为第一要求，为防发生事故，结合永磁静态强吸力的特点，选用永磁吸附作为机器人的吸附系统。

针对现有移动机器人研究常用的3种方式进行对比分析，见表2。其中轮式机器人具有结构简单、操作性好、运动速度快、转向力矩小且控制系统简单等优点，后期还可以通过Halbach阵列的磁轮结构解决磁力不足的问题。

表1 爬壁机器人吸附方式优缺点比较

表2 爬壁机器人行走方式优缺点比较

1.2 磁轮设计及磁优化

如图1所示，设定单个机器人模块重力为G，假定重心在O处，重心相对壁面高度为H，壁面对磁轮的吸引力为Fm，壁面的机器人的支持力为Ni，壁面对机器人的摩擦力为Ff。

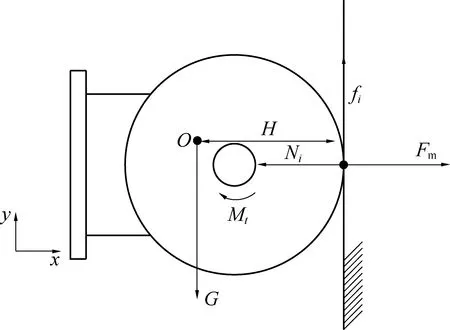
图1 单节机器人受力分析Fig.1 Force Analysis of single-unit robot

根据2个方向的受力平衡，有：

（1）

式中：Fm为壁面对磁轮的吸附力；Ni为钢罐道壁面对第i个车轮的反作用力。

（2）

式中：fi为壁面对机器人的静摩擦力；m为机器人模块质量；k为垂直爬行的安全系数，取k=2。

向上运动时，摩擦力做正功，推动它向前行驶，为避免巡检机器人打滑，要求两磁轮所产生的最大摩擦力之和要大于机器人重力：

（3）

其中:μ为轭铁材料与钢罐道壁面的静摩擦系数。

根据直线运动时的力矩平衡，有：

（4）

其中：Mt为电机提供额定力矩。

1）磁轮优化目标。在钢罐道壁面厚度参数一定的情况下（姑且认为气隙趋近于0），磁铁吸附力、磁能利用率以及磁铁重量与磁铁本身结构参数紧密相关，故这三者之间会存在一定的耦合关系。我们将磁轮性能优化目标定义为磁能密度系数[22]，其表示符为λ，值由式（5）给出：

λ=Fx/Gc

（5）

其中：Fx为磁轮与钢罐道之间的吸附力；Gc为磁轮自身重量。优化目标是寻找最优的磁轮参数，使在吸附力不变的情况下，磁轮重量最轻，即λ最大化。

2）磁场计算理论基础。磁轮产生的磁场为静态磁场，利用麦克斯韦基本电磁场理论进行分析。

安培环路定律：

（6）

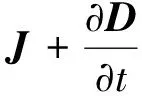
磁场的边界条件如下：

B=μ0μrH=μH

（7）

其中：B为穿过闭合曲线限定面积的磁通；μ0为真空磁导率；μr为磁介质的相对磁导率；μ为磁介质的磁导率。

高斯磁通定律：

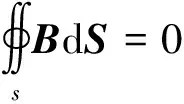
（8）

图2为磁轮轭铁尺寸示意。由实际测量可计算出，在磁轮直径为30 mm的情况下，磁铁厚度在17 mm时，可产生40 N的磁吸力，此时机器人可以安全地吸附于钢罐道壁面上。

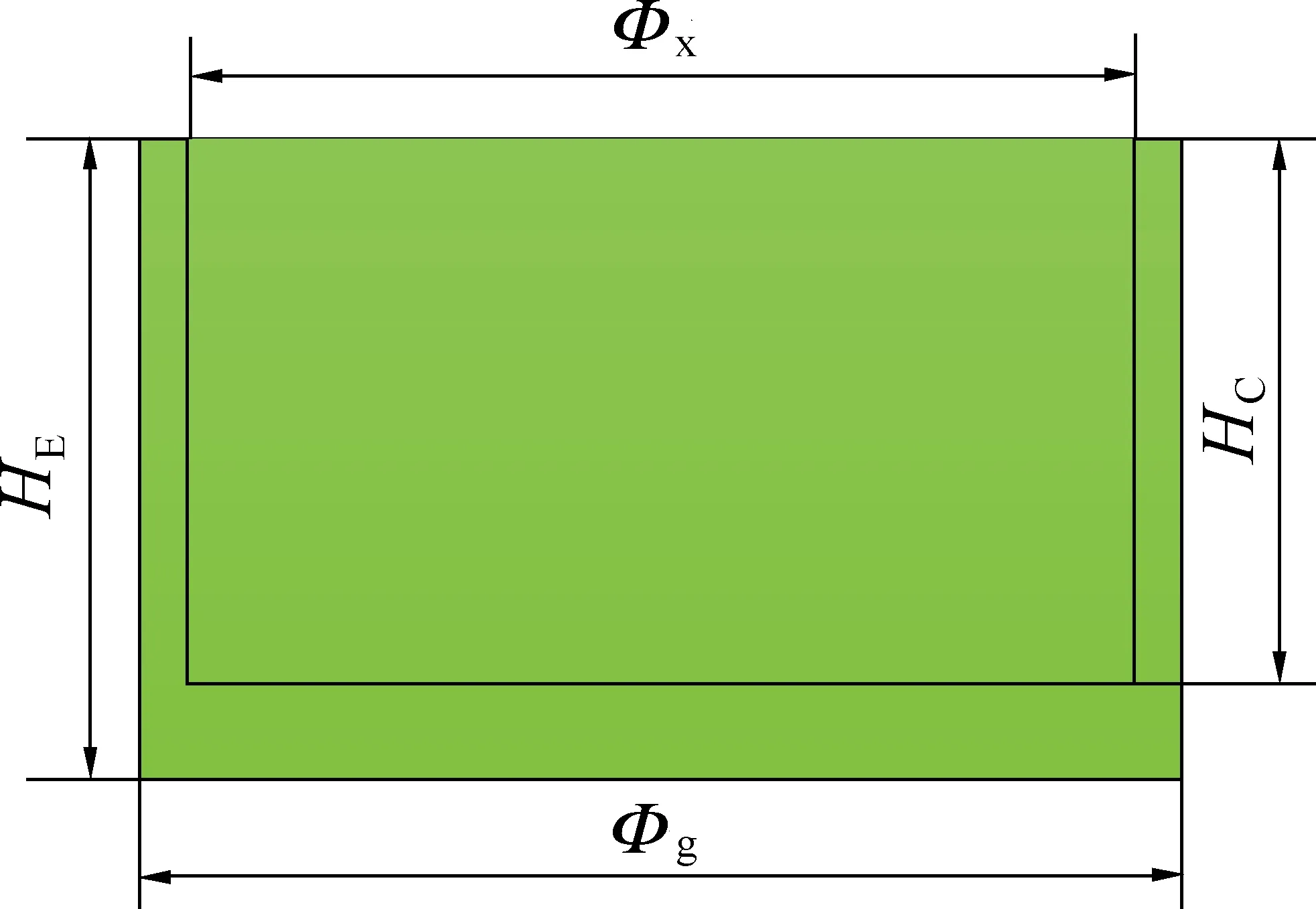
图2 磁轮轭铁尺寸Fig.2 Dimensions schematic of magnetic wheel and yoke

取相同吸附力Fm=57.9 N（仿真值）情况下，磁铁直径不同时，磁铁磁能密度系数的大小。模拟结果表明，在相同吸附力下，随着磁轮直径的增大，磁体质量逐渐增大，磁能密度系数逐渐减小。

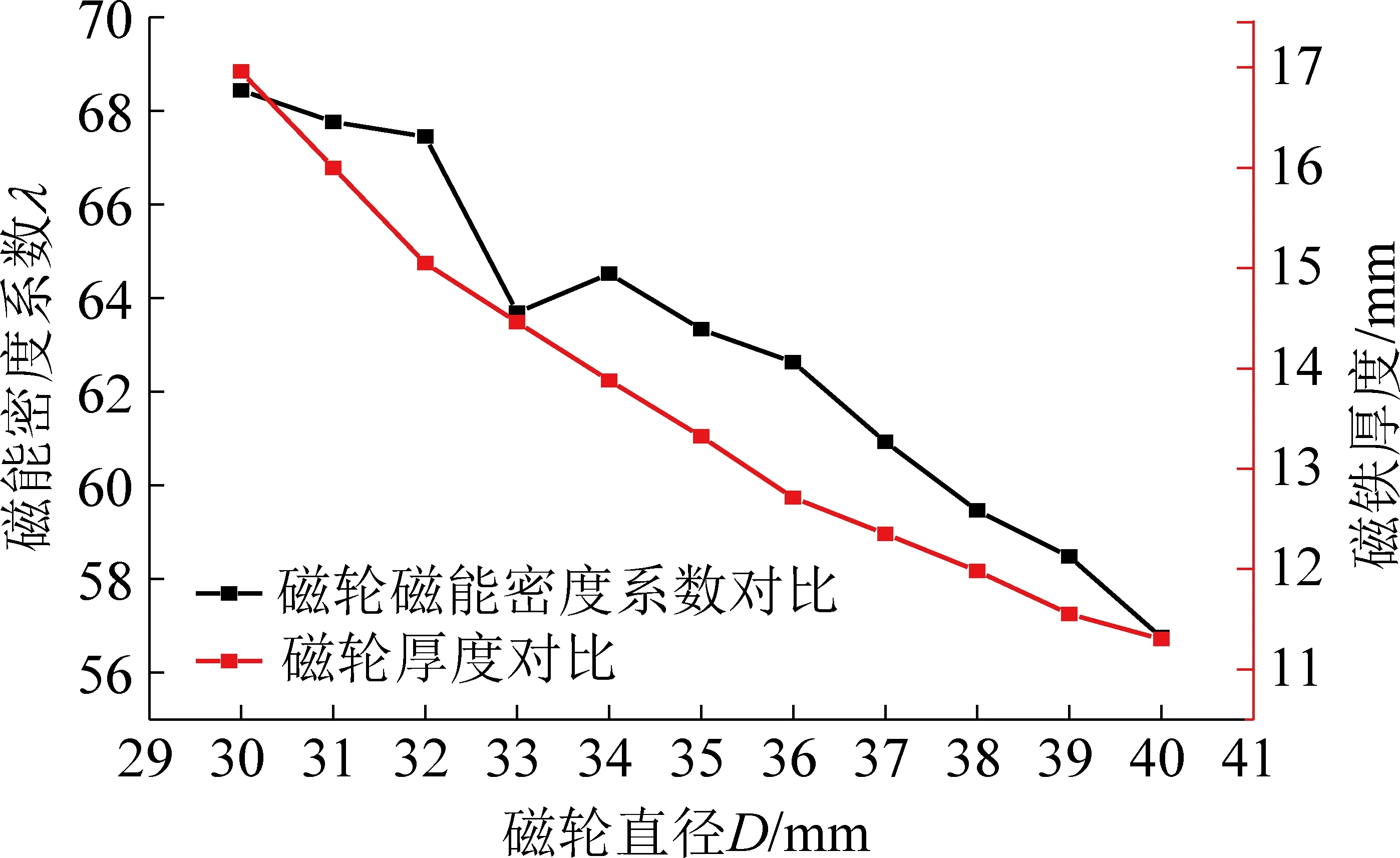
图3 相同磁力不同直径磁轮磁能密度系数及磁铁厚度对比Fig.3 Comparison of magnetic energy density coefficient and magnet thickness of magnetic wheels with the same magnetic force and diameter

图4 相同磁力不同直径磁轮磁能密度系数及磁铁质量对比Fig.4 Comparison of magnetic energy density coefficient and magnet quality of magnetic wheels with the same magnetic force and diameter

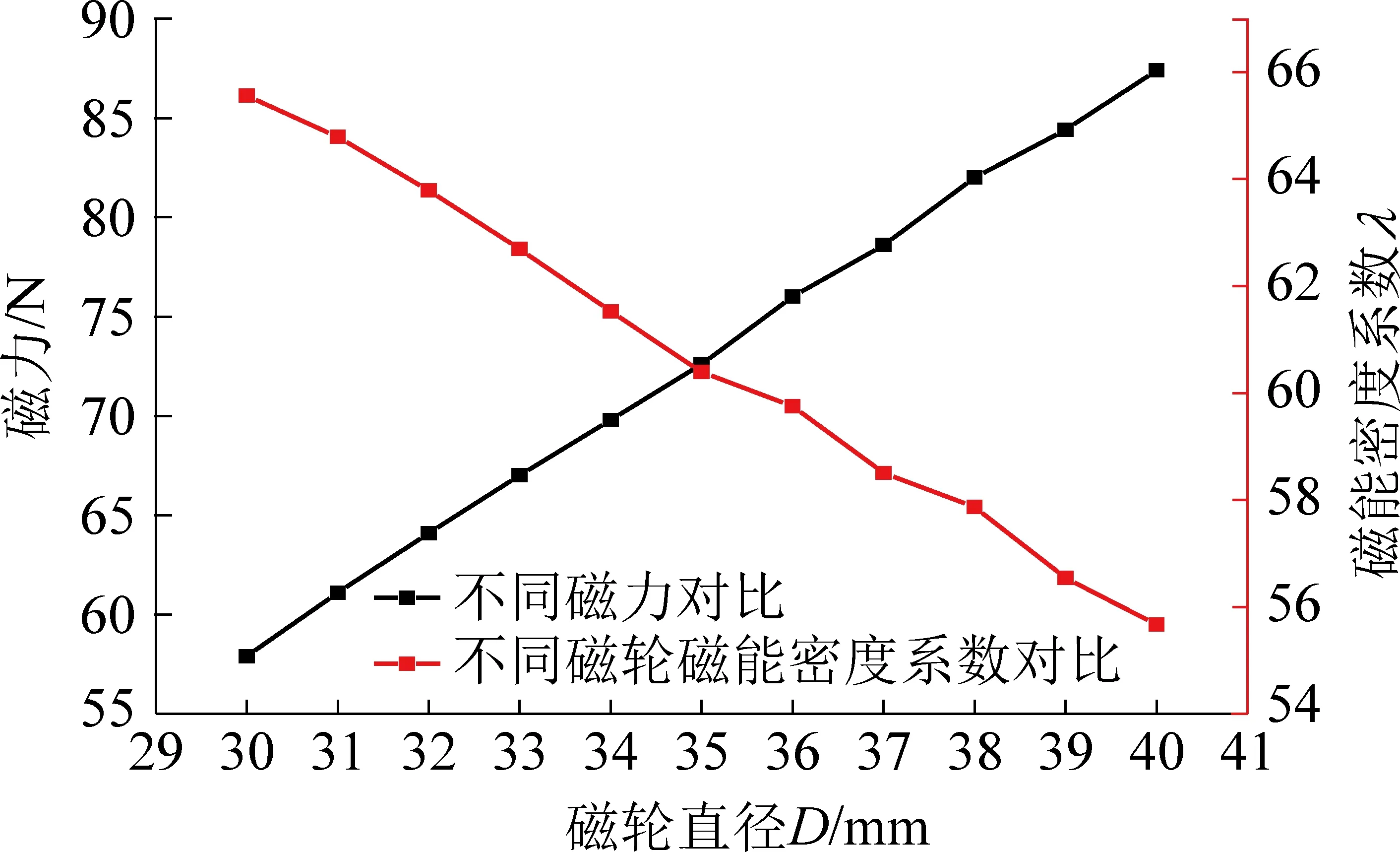
图5 厚度相同直径不同磁轮磁能密度系数及磁力对比Fig.5 Magnetic energy density coefficient and magnetic force contrast diagram of magnetic wheel with the same thickness and different diameters

综合图3—图5可以看出，当磁吸附力不同（磁轮直径不同，厚度相同）时，磁吸附力随磁轮直径的增大而增大，而磁能密度系数随磁轮直径的增大而减小。

1.3 机器人总体结构

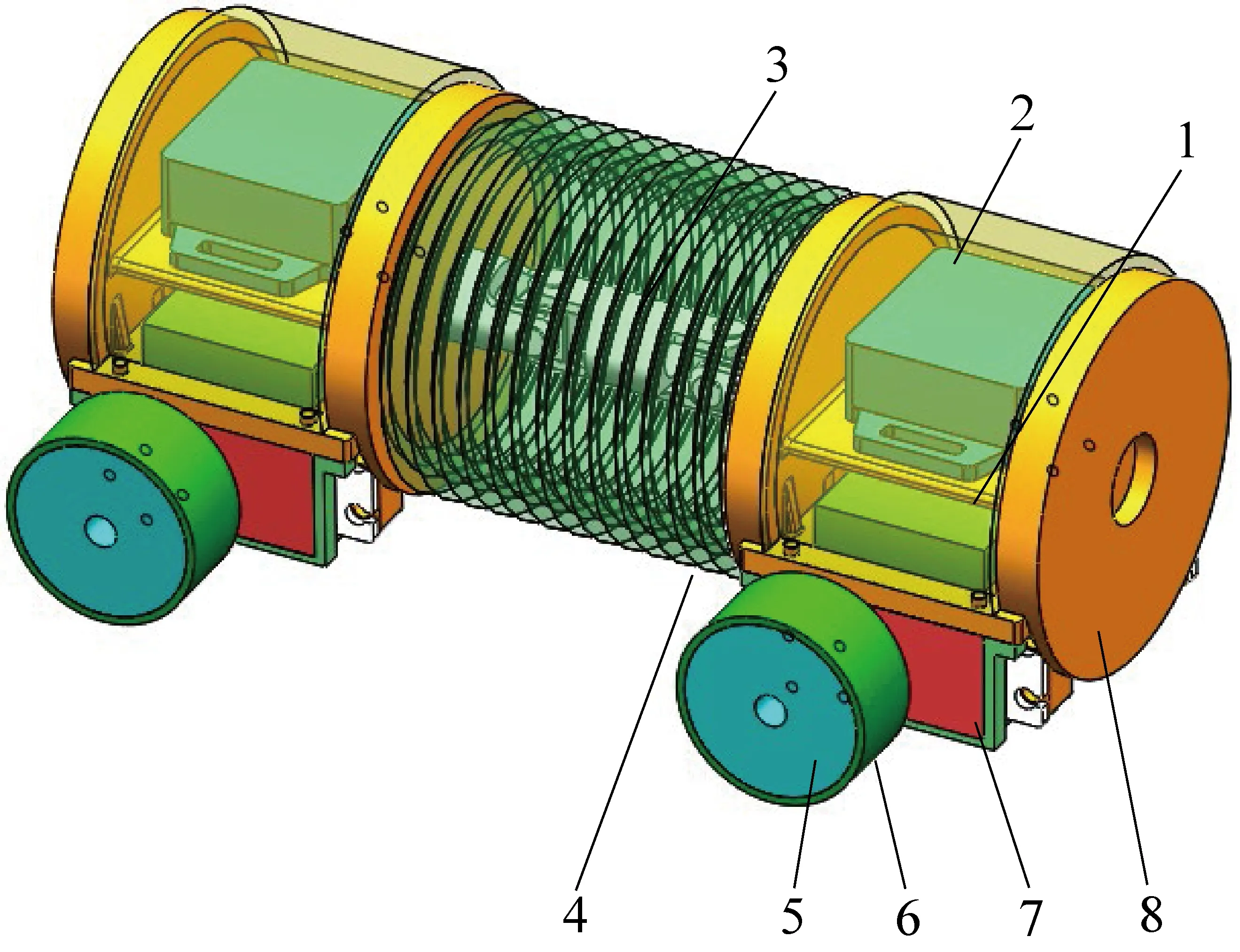
1—电源模块；2—传感器模块；3—万向节；4—波纹管；5—磁轮；6—轭铁；7—驱动舵机；8—底板外壳图6 钢罐道巡检机器人三维造型Fig.6 Three-dimensional modeling of rigid cage guide inspection robot

钢罐道巡检测机器人主要由以下8部分组成：底板外壳采用ABS材料进行3D打印加工；驱动装置为高度集成的连续旋转转向器；2个单元之间采用万向节连接；传感器模块采用JY-901姿态模块；电源模块采用7.4 V、5 000 mAh锂电池。

表3 钢罐道巡检机器人技术指标

2 步态规划及仿真

2.1 姿态估计

巡检机器人的姿态估计系统框流程如图7所示。为确保MARG传感系统能输出准确、稳定的姿态角，本研究将陀螺仪、加速度计、磁强计所输出的测量值通过扩展卡尔曼滤波算法进行多传感器的信息融合。

系统模型建立：

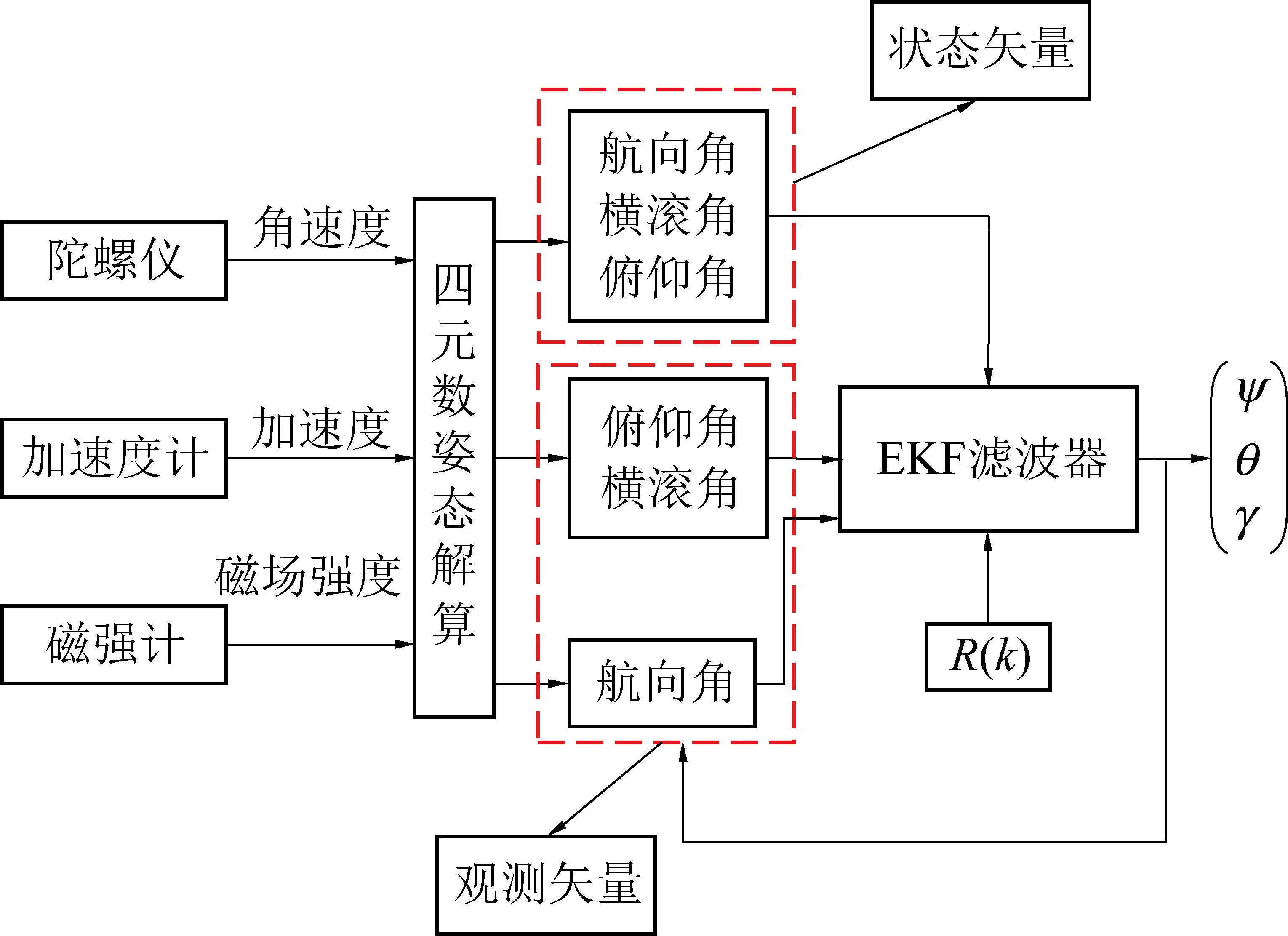
图7 姿态估计系统流程Fig.7 Flow of the attitude estimation system

（9）

其中：x（k）∈Rn为系统在K时刻的状态预测矢量；uk-1为K时刻的控制输入；ωk-1为过程激励噪声Q（k）的协方差；zk为K时刻的观测真值；vk为观测噪声R（k）的协方差。

设系统非线性状态方程为：

（10）

其中：q0（k），q1（k），q2（k），q3（k）为K时刻姿态的四元数；ωxb（k），ωyb（k），ωzb（k）分别为K时刻陀螺仪角速度偏置误差。

设系统观测方程为z（k）=[axb（k）ayb（k）azb（k）ψm（k）]T。其中axb（k），ayb（k），azb（k）分别表示载体坐标系中三轴加速度值；ψm（k）表示通过磁强计所计算得出的航向角。

当机器人静止或保持匀速直线运动时，如式（13）所示。

（11）

（12）

系统的观测方程为：

（13）

对h（x（k）,k）求取雅克比矩阵：

（14）

建立好关系后，姿态更新系统通过图8的姿态解算算法循环。

通过以上对姿态估计算法的设计，对其进行仿真分析，如图9所示，可看出其状态测量与真实状态相差较大，通过EKF进行姿态最优估计，其估计值与姿态真实状态相近，其偏差图如图10所示，浮动范围在±0.1°内，证明该姿态估计算法是可靠的。

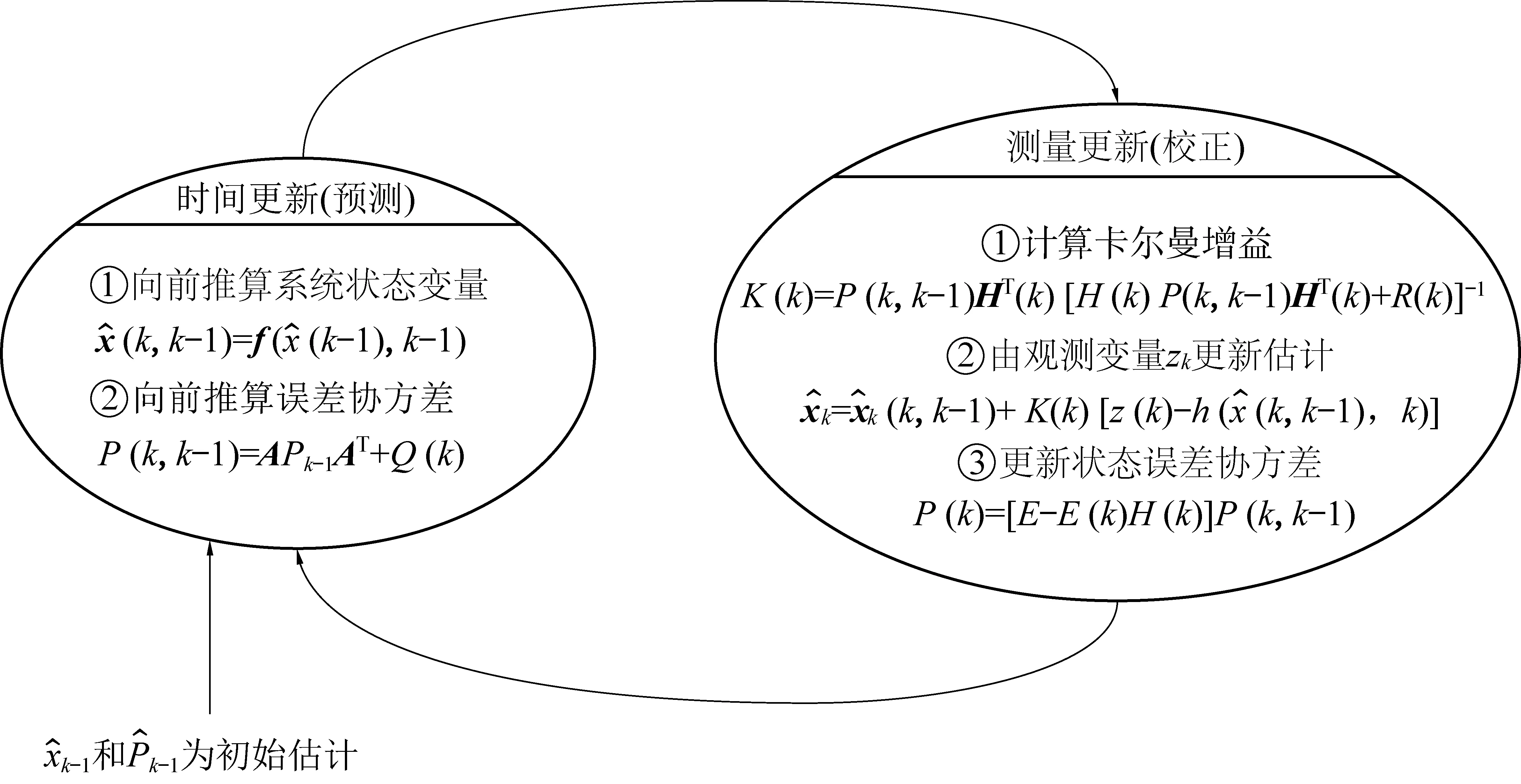
图8 基于扩展卡尔曼滤波姿态解算算法流程Fig.8 Program flow of attitude algorithm based on extended kalman filter

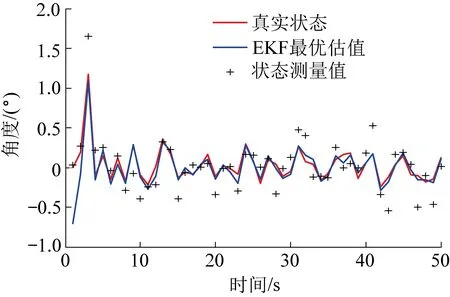
图9 基于EKF滤波姿态估计仿真分析Fig.9 Simulation and analysis of attitude estimation based on EKF filter

图10 基于EKF滤波姿态估计偏差Fig.10 Attitude estimation deviation map based on EKF filter

2.2 反步法轨迹追踪

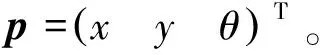
当磁轮与地面无滑动时，则运动学方程为：

（15）

非完整约束为：

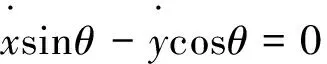
（16）

巡检机器人期望位姿为（xr,yr,θr）T，实际位姿为：（xc,yc,θc）T，在全局坐标系内位姿偏差为（xr-xc,yr-yc,θr-θc）T，机器人局部坐标系内偏差为：

（17）

其中：θe=θR-θC；θR、θC分别为R点和C点的方向角。

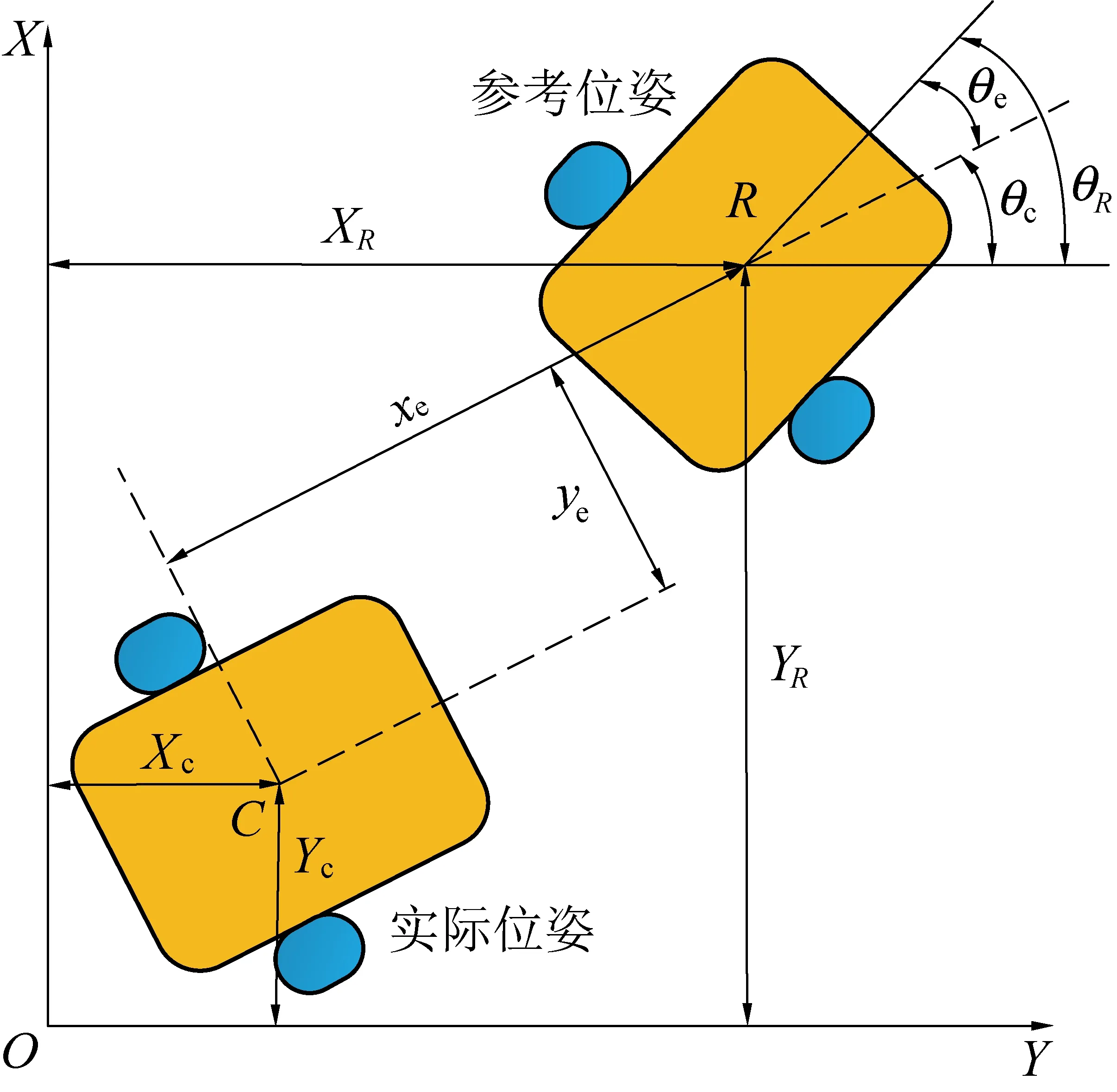
图11 巡检机器人运动学模型Fig.11 Kinematics model of inspection robot

由式（16）得：

（18）

由式（18）得：

对式（18）求导可得机器人误差微分方程为：

（19）

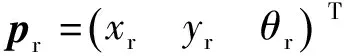
考虑到巡检机器人系统的复杂性和非完整约束，Backstepping方法是一种将不确定系统系统化的控制器综合方法。通过递归构造闭环系统的Lyapunov函数，得到反馈控制器。为此，采用backstepping方法设计了巡检机器人的轨迹跟踪控制律设计原理如图12所示。

图12 机器人轨迹追踪控制框Fig.12 Robot track tracking control block diagram

首先当xe=0时，选取控制Lyapunov函数为：

（20）

对V1微分可得：

（21）

其次：在V1的基础上选取Lyapunov函数为：

（22）

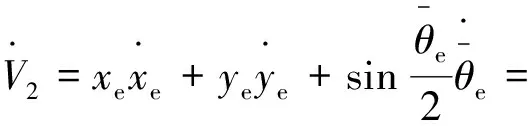
（23）

故将轨迹跟踪控制率设为：

（24）

式中，β为虚拟控制量；k1，k2为正数。

最后对其稳定性进行分析，取Lyapunov函数为：

（25）

则有：

（26）

式中，k1，k2均不小于0，yevrsin[arctan（yevr）]≥0，可得V≤0，即V为负定连续函数，使得t→∞时，V→0，根据Lyapunov稳定性判断方法可以得出系统是稳定的。

对爬壁巡检机器人系统的轨迹跟踪过程进行仿真分析。使检测机器人分别跟踪给定的直线轨迹、圆轨迹。

1）参考轨迹为直线。具体参数为：跟踪直线为y=1.73x-1.73，初始偏差（0.2，-2，0.53），选取k1=5,k2=5。参考线速度为vr=0.2,ωr=0.2，具体仿真结果如图13所示。

图13 基于运动学模型反步法跟踪直线轨迹结果Fig.13 Tracking straight line trajectory based on kinematics model backstepping method

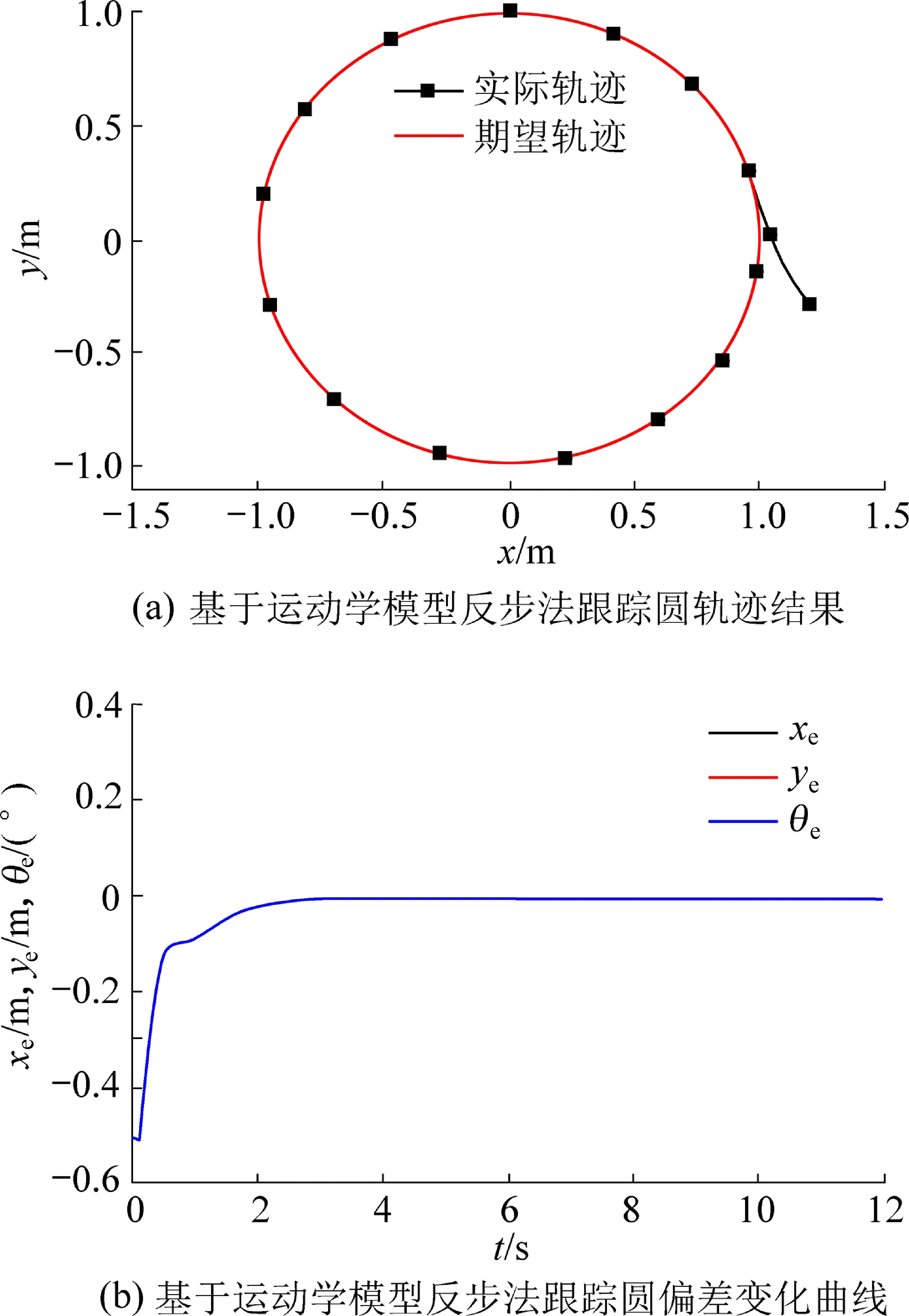
图14 基于运动学模型反步法跟踪圆轨迹结果Fig.14 Tracking circular trajectory results based on kinematic model backstepping

2）参考轨迹为圆。具体参数为：跟踪圆为x2+y2=1，初始偏差（0.2，-0.32，0.5），选取k1=5,k2=5。参考线速度为vr=0.2,ωr=0.2，具体仿真结果如图14所示。

根据直线和圆轨迹跟踪的仿真结果，当跟踪时间达到3 s时，局部位置误差趋于稳定并收敛到零，说明在控制器的作用下，爬壁机器人能够实现直线和圆轨迹的快速、准确的轨迹跟踪。当轨迹比较复杂时，局部位置误差总是存在的，但总体收敛到0，因此本研究提出的基于backstepping方法设计的控制器能够满足爬壁机器人轨迹跟踪的要求。

3 巡检机器人运动轨迹试验

基于MARG传感器测量单元，结合EKF滤波算法，实现了爬壁机器人的实时姿态估计，主要是二维位姿估计，即平面位姿估计和空间位姿估计。平面姿态估计是检测机器人在钢罐道单壁上的姿态估计和反馈；空间姿态是检测机器人在钢罐道单壁上的姿态估计和反馈。当检测机器人在壁面上处于过渡步态时，前面部分可能已经通过壁面，而后面部分仍然在原来的壁面上。利MARG传感器测量单元实时反馈检测机器人此时的位置和姿态，从而规划检测机器人的下一步运动轨迹，试验平台如图15所示。

3.1 平面姿态评估

巡检机器人在单壁面上进行直线行驶，其偏航角随时间变化如图16所示。通过MIMU传感器所返回的数据我们可以看出，由于机器人制造误差以及舵机特性不一造成巡检机器人在进行直线行驶时其偏航角会浮动在2°以内。

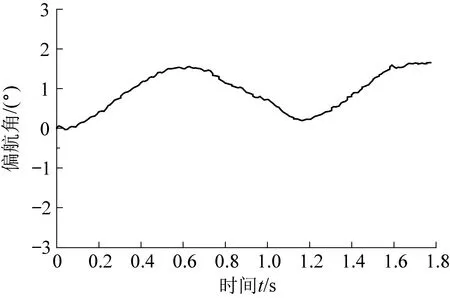
图16 巡检机器人在单壁面直线行驶偏航角随时间变化Fig.16 Variation of yaw angle with time of inspection robot traveling in a straight line on a single wall

3.2 壁面过渡姿态估计

当检测机器人检测到钢罐道单壁存在缺陷或损坏时，或当加速度计检测到特强振动信号时，检测机器人会自动爬到另一侧。运动过程如图17所示。

图17 机器人进行跨壁面运动示意Fig.17 Schematic of robot moving across the wall

当其完成翻越动作时，其俯仰角会发生90°的跳变，如图18所示，通过在上位机观察巡检机器人所携带MARG传感测量单元所检测出姿态角的变化，判断其是否完成翻越动作。

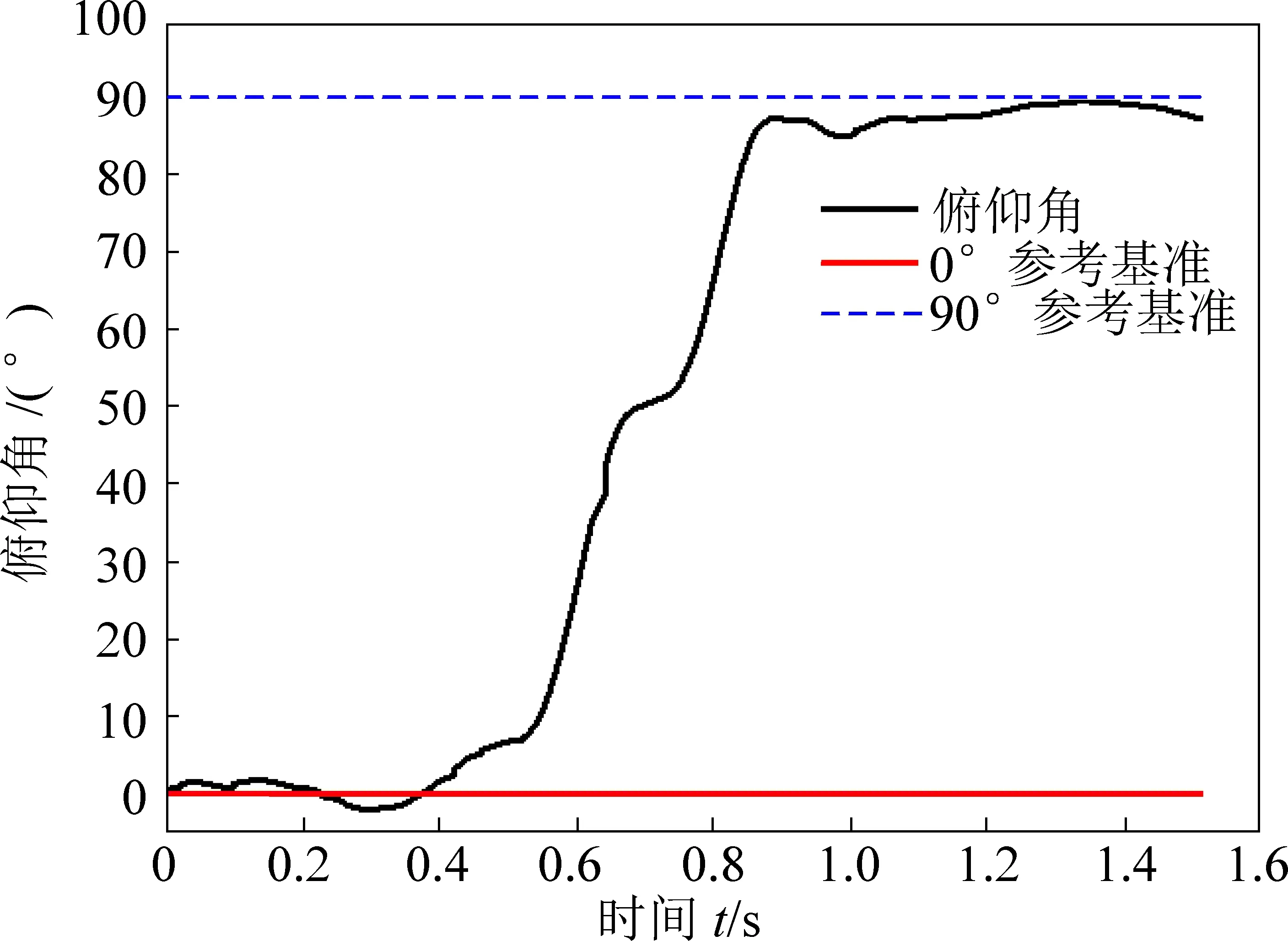
图18 巡检机器人跨壁面运动时俯仰角随时间变化Fig.18 Pitching angle versus time of inspection robot moving across Wall

3.3 机器人轨迹追踪试验

1）机器人直线行驶轨迹追踪分析。给定左右侧舵机转速相同，且在机器人底部安装了一个记号笔，测试机器人在直线行驶时的轨迹，试验结果如图19所示。

图19 机器人直线行驶运行轨迹线Fig.19 Robot straight running trajectory

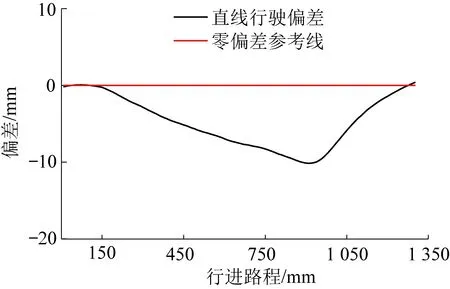
图20 直线轨迹追踪偏差Fig.20 Deviation of straight track tracking

巡检机器人在直线行驶时的偏差如图20所示，由于左右磁轮品质不一，导致机器人在初始阶段偏离了航线，由控制系统对其航向角进行反馈，当其航向角超过1°时开始进行自我调整，所以在前进900 mm后机器人开始回归原始航线。

2）机器人转弯行驶轨迹追踪分析。给定左侧舵机转速为0.1 m/s，右侧舵机转速为0，转弯半径为49.5 mm。测试机器人在转弯行驶时的轨迹，试验结果如图21所示。

巡检机器人在进行转弯轨迹追踪时，由0°转动至90°其转弯半径的变化，变化如图22所示，由图可看出，在转弯初始阶段，出现一定的偏差，当偏差达到1 mm左右时趋于稳定。该偏差可能是有测量方法、机器人安装误差、试验环境不够标准等造成的。

图21 转弯轨迹追踪Fig.21 Turning trajectory tracking

图22 转弯轨迹追踪转弯半径随转角变化Fig.22 Turning trajectory tracking turning radius changing with turning angle

4 结 论

1）通过分析机器人在钢罐道上可靠运行的条件，设计并研制了机器人样机，进一步对机器人的磁轮结构尺寸进行了优化分析，为实现钢罐道全面巡检提供了硬件基础。

2）通过研究EKF滤波算法并结合MARG传感测量单元，建立了状态方程，利用matlab进行算法仿真分析，实现了对机器人当前姿态的估计。

3）建立了巡检机器人在罐道面上的运动学模型，并利用反步法设计控制器，在仿真环境中实现了直线和圆轨迹的快速、准确跟踪。

4）最后进行了罐道攀爬试验，结果表明：所设计的巡检机器人能够进行壁面跨越；左右两侧舵机转速为0.1 m/s，转弯半径为49.5 mm时，可实现0°～90°的转弯。试验验证了所设计样机在钢罐道上进行全面巡检的可行性。