基于贝叶斯法估计龙竹人工林叶面积指数模型

孙 杨 舒清态 黄金君 席 磊 刘玥伶 罗 浩

（西南林业大学林学院，云南昆明 650233）

叶面积指数（LAI）是森林生态系统研究中的重要参数之一，是植物光合作用、蒸腾作用、水分利用及初级生产力构成中的重要指标[1]，在估算多种生态功能和过程中起到关键变量的重要作用[2]。叶片是植物与自然界进行能量交换的重要通道，在不同环境和植被条件下具有不同程度的健康状况，因此叶片可用于间接反应森林植被信息[3-4]，同时也决定了陆地植被的生产力水平。快速地获取林分LAI对于不同生态系统研究具有重要意义[5]。目前对LAI的估测方法大体分为直接测量和间接测量[6]，由于森林覆盖面积大且结构复杂多样，直接测量法对物力、财力和人力的消耗很大，对森林造成的破坏也很严重。间接测量法消耗时间少，对森林的破坏也小。采用异速生长方程估测LAI可减少大量工作量，有许多研究采用异速生长方程进行模型研究，如Vyas等[7]以柚木（Tectona grandis）和印度实竹（Dendrocalamus strictus）为研究对象构建异速生长方程对LAI进行研究，决定系数（R2）达到0.94。王柯人等[8]基于异速生长方程对高山松（Pinus densata）生物量模型进行研究，采用非线性最小二乘法进行估算，R2高达0.90以上。Zhang等[9]通过建立胸径和叶面积指数之间的指数关系，构建林分叶面积指数模型，预测了长白山多种树种的LAI，R2均能保持在0.80以上。该方程符合林分的生长规律，其参数的拟合方法可采用传统统计学方法，传统统计学方法操作简单，但只考虑了样本信息，忽略了样本之间的区域、层次效应，模型参数估测精度有待提升[10]。而贝叶斯方法充分利用调查对象样本信息与先验信息，分别从定性、定量两个角度诠释了模型参数特征，且具有良好的稳健性[11]。贝叶斯模型是一种有效描述数据集合评估参数不确定性的方法[12]，已经在医疗、生态、水文、环境等领域得到广泛应用[13]，如李向阳[14]采用贝叶斯方法求解出流域水文模型各参数的后验分布，且求解出的参数质量好。贝叶斯方法在林业领域研究中应用同样广泛，常用于林木的直径分布、胸径树高生长模型、胸高断面积模型、单木竞争模型、枯死模型、生物量模型及其他应用[15-18]。而基于贝叶斯统计对叶面积指数模型的研究却少有报道。混合模型和分层贝叶斯模型在拟合叶面积指数时，能考虑到区域位置对叶面积指数的影响[10]，混合模型既能体现总体平均变化趋势，又可体现区域之间的差异[19]，因此非常适用于具备多层次，多区域的数据[20]。

龙竹（Dendrocalamus giganteus）又名苦龙竹，在云南省栽培最为广泛[21]。它的秆茎笔直粗大，成材时间短，是良好的建筑和篾用竹材。国内目前对竹类植物研究开发最全面的是毛竹，其种植面积占全国竹林面积的73%[22]。而对龙竹的研究鲜有报道，因此本研究采用野外调查样地数据结合异速生长方程对沧源县和新平县的丛生龙竹叶面积指数进行估测，并利用非线性最小二乘法、贝叶斯法和分层贝叶斯模型进行模型拟合，比较3种方法的预估精度，对丛生龙竹叶面积指数模型进行探索，为日后森林叶面积指数精确估测提供服务。

1 研究区概况

以云南省新平县和沧源县为研究区。新平县地处哀牢山中段东麓，位于23°38′～24°26′ N，101°16′～102°16′E，属温带气候区。沧源县地处23°04′～23°40′ N，98°52′～99°43′E，属亚热带低纬山地季风气候，位于中缅边界中段，北接耿马傣族佤族自治县，东与双江县相连，南面与缅甸掸邦第二特区勐冒县相邻，西面与南邓特区接壤[23]。全境最高点海拔2605 m，最低450 m，年平均气温17.2℃，富含丰富的珍稀动植物资源。龙竹的气候条件要求年均温大于17℃，且具备一定的耐瘠薄能力。随着我国经济快速发展及全球化发展的不断深入，对龙竹的需求自然会增加。因此，对龙竹长势进行监测，推动龙竹产业可持续发展，最终实现定性定量对龙竹冠层结构信息研究是十分重要的。

2 材料与方法

2.1 数据采集及整理

所需数据包括实测丛生龙竹叶面积指数（LAI）、胸径（D），分别在沧源县、新平县设计20 m ×20 m的方形样地23块和50块，对每块样地进行每木检尺，测定胸径、坐标、LAI等因子。胸径的起测径阶设置为4 cm，每块样地的坐标使用RTK进行测量。实测叶面积指数主要通过LAI-2200植被冠层分析仪获取。LAI2200是基于LAI-2000开发的，其原理利用鱼眼光学传感器在5个不同的天顶角方向来检测植物冠层下方光照强度变化，测量时的最佳状态应为云层均匀分布的阴天[24]。选取的仪器模式为“ABBBB”模式，即在每块样地测量1个天空空白作为“A”值和4个在林下测量得到的“B”值，通过LAI-2200匹配的软件中进行计算得出每块样地的平均值，共采集73块地面样地数据，经过整理分析，统计数据如表1。本试验所选的2个地区地理位置差异较大，气候条件也不同，从沧源县的亚热带低纬山地季风气候到新平县的温带气候，气候上的巨大差异对龙竹的生长状况必将产生影响，因此将新平县划分为I区域，沧源县划分为II区域。

表1 龙竹实测样地数据统计表Table1 Statistics of measured plot data of D. giganteus

2.2 LAI基础模型构建

有研究表明胸径、树高、冠层郁闭等因子与LAI之间存在很好的相关性[25]，本研究选用Zhang等[26]构建的LAI模型为基础模型，以此估测龙竹叶面积指数，所构建的模型如下：

式中：LAI代表林分加权叶面积指数，a和b为模型的参数。

而龙竹与其他散生竹的生长方式有很大差异，龙竹以丛为单位生长，平均每丛龙竹有10棵龙竹，这对于测定龙竹单木水平上的LAI是一个难点，因此需对基础模型进行进一步转换。本研究以断面积（G）为权重因子，所构建的模型如下：

2.3 模型拟合方法

2.3.1 最小二乘法

最小二乘算法在经典统计学中是一种常见和普遍采用的逼近算法，其基本原理是通过不断迭代和替换线性函数以达到与非线性函数的平方和最小，从而求解出参数的最优解。公式为：

式中：argmin为最小化函数，LAIi为龙竹叶面积指数的实测值，aDb为龙竹叶面积指数的估计值，采用当龙竹叶面积指数实测值与估测值平方和最小求出参数a和b。

2.3.2 贝叶斯方法

贝叶斯统计学与传统统计学是现今世界两大统计学派，且具有不同的统计推断理论，贝叶斯统计主张把待估参数（θ）看做随机变量，在抽样前就具有先验分布，且贝叶斯方法充分考虑了样本信息和先验信息，从而在样本量小的情况下最大程度弥补信息的缺失[27]，而传统统计学派则把θ视为固定的未知参数。贝叶斯方法的核心就是对后验分布的计算，而后验分布马尔科夫链蒙特卡罗（MCMC）方法的应用，解决了后验分布复杂计算的问题。

贝叶斯统计估测法和层次贝叶斯统计法都可以获取叶面积指数经验模型中的参数。先验信息是贝叶斯统计中的关键因素，贝叶斯中的先验信息可通过前人研究成果或主体经验获取。当对参数了解较少时，常选取正态分布表示先验分布[28]。当有丰富的先验信息时，先验分布可根据先验信息构建[29]。贝叶斯公式是贝叶斯统计的核心，其基本形式为：

式中：P(B|A)表示在事件A发生的条件下，事件B的概率，P(A|B)是后验分布。

在本研究中，假设模型的表达形式如下：

式中：y是模型的因变量，x是模型中的自变量，θ是模型中的待估参数。

假设y作为样本向量，θ为参数向量，那么上述公式可以概括为：

式中：对于给定样本数据y的θ条件分布即π(θ|y)就 是需求算的后验分布，P(y|θ)是y的似然函数，而π(θ)为当样本信息不清楚时的θ的分布。

分层贝叶斯是以贝叶斯为理论基础，设置多层先验求出参数的方法[30]。混合模型具有明显的层次结构，即固定效应和随机效应，固定效应包含与总体有关参数，随机效应是与总体中的个体有关的量。随机效应为模型再增加了一个层次，既可以反映总体的一般变化趋势，又可反映个体间的差异。在贝叶斯模型中，此类模型使用分层贝叶斯进行分析。本研究主要考虑了不同区域的随机效应，将数据分为2层，第1层是时空间的不同区域LAI数据，第2层是时空内样本的LAI和胸径。混合模型在林业方面已有研究[31-32]，其参数估计主要采用最大似然或最小二乘法进行估计。贝叶斯统计方法本身就有层次性，而分层贝叶斯统计方法是对参数a再增加一个层次，即再将先验信息赋予先验参数。其基本形式如下：

在贝叶斯统计中，后验分布的计算结果是十分重要的，主要是由似然函数、先验分布及一个积分的形式构成，其计算方法主要采用马尔科夫链蒙特卡罗（MCMC）模拟法计算。

针对贝叶斯方法的参数估计，主要运用由Andrew Thomas在赫尔辛基大学研发的OpenBUGS软件，其理论与方法和WinBUGS软件基本相同[33]，即采用吉布斯抽样算法[34]和MCMC方法估计参数，对于传统统计方法的参数估计主要在R软件下完成。本研究为保证迭代收敛以及获取可靠的参数值，设置迭代次数为3万次，并将前面的1000次作为退火迭代舍去，为减少相邻链的相关性，设置链条数为3条。设置的有先验信息贝叶斯法和分层贝叶斯模型先验信息见表2。

表2 先验信息Table 2 Prior information

2.3.3 模型评价

本研究拟从三个方面，包括模型精度、拟合优度以及参数稳定性对模型进行综合评价，模型精度主要包括均方根误差（RMSE），估测精度（E），模型拟合优度主要采用决定系数（R2），参数稳定性主要由置信区间和可信区间表示，各评价指标计算方法见式（10）～（12）。

3 结果与分析

3.1 分层贝叶斯估计结果分析

通过计算非线性混合效应模型估计的参数值作为分层贝叶斯的先验信息，以2个不同区域作为随机效应，通过比较AIC值构建适合的随机效应模型，最终选用将随机效应作用在参数b上。分层贝叶斯参数后验概率的计算采用MCMC方法估计，计算结果见表3。2个区域的参数a均值为0.0025，第1区域的参数b均值为1.162，第二区域的参数b均值为0.9594。利用分层贝叶斯方法估测参数的后验概率核密度图见图1。由图1可知，待估参数a、b1、b2的后验概率核密度图都呈现出正态分布，但加入了随机效应后参数b1、b2较稳定，各参数结果通过显著性检验（P＜0.05），说明相关性较好。

图1 分层贝叶斯参数后验概率分布Fig.1 Posterior probability distribution of hierarchical Bayesian parameters

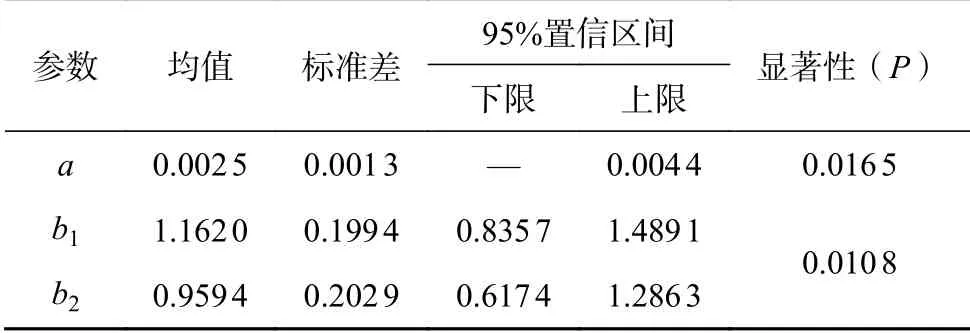
表3 分层贝叶斯参数估计结果Table 3 The results of hierarchical Bayesian parameter estimation

3.2 不同方法估测结果比较分析

采用最小二乘、有先验信息贝叶斯和分层贝叶斯3种方法对模型参数拟合后的结果与评价指标见表4。由表4可知，最小二乘法、有先验信息贝叶斯方法和分层贝叶斯方法的R2和RMSE分别为0.4875、0.4874、0.6733和0.0071、0.0070、0.0057，估测精度值E分别为75.31%、75.31%和80.27%。其中，分层贝叶斯方法的R2最高，达到0.6733，通过观察95%的置信区间可发现，有先验信息的贝叶斯方法估测参数置信区间比传统方法窄，这说明通过贝叶斯方法估测得到的参数要比传统法的可靠。而分层贝叶斯方法的各待估参数置信区间比最小二乘法，先验信息贝叶斯法窄，因此基于分层贝叶斯法估测的参数更加可靠、稳定。通过比较RMSE值，贝叶斯方法要略好于最小二乘法，分层贝叶斯法明显优于其他2种估测方法；且对比估测精度发现分层贝叶斯法的拟合精度表现最好。观察偏差信息准则（DIC）值可发现，分层贝叶斯模型的效果优于有先验信息贝叶斯模型。

表4 3种拟合方法结果及评价指标Table 4 Theresultsof 3 fitting methodsand evaluation indexes

采用最小二乘、贝叶斯方法和分层贝叶斯方法预估的待估参数进行拟合龙竹叶面积指数估测值与林分加权叶面积指数值见图2。由图2可知，采用分层贝叶斯方法估测的效果是最好的，其预测值与实测值相近波动小，同时与其他2种方法相比R2从0.4882提高至0.6753，这表明分层贝叶斯方法估测精度是最高的，预测效果是最好的。而以最小二乘结果作为先验信息的贝叶斯方法，其拟合结果与最小二乘方法相近，结果为0.4882，这是因为贝叶斯方法充分利用了样本信息和先验信息，同时由于加入随机效应，使得分层贝叶斯方法的估测值更加可靠、稳定。采用十折交叉验证法后，相关评价统计指标如表5，从检验样本的验证效果来看，分层贝叶斯法的效果对比其他2种方法同样有较大提升。

图2 不同方法叶面积指数实测值与估计值对比Fig.2 Comparison of measured and estimated leaf area index by different methods

表5 检验样本的相应评价指标Table5 Thecorresponding evaluation indexesof test samples

4 结论与讨论

本研究旨在探索基于异速生长方程模型的叶面积指数估测，分别利用传统统计学方法（非线性最小二乘法）和贝叶斯方法估测小尺度林分上叶面积指数估测模型参数。研究发现：

1）传统统计法（非线性最小二乘法）在估测叶面积指数模型参数时，R2对比有先验信息贝叶斯法有小幅提升，但RMSE略低于有先验信息贝叶斯。这表明利用非线性最小二乘方法拟合叶面积指数模型参数时出现过拟合现象，这可能由样本数量较小所导致。Zapata-Cuartas等[35]通过构建单木生物量模型，比较最小二乘法和贝叶斯法对不同样本量拟合的估计效果，结果表明，样本量小时参数置信区间对比样本量大时的参数置信区间要宽，同时，贝叶斯法的参数置信区间对比最小二乘法更加集中，且贝叶斯法的偏差和均方根误差都比最小二乘法更为稳定，并随着样本量到达一定程度时趋于统一。本研究建立的贝叶斯模型没有出现过拟合现象，估测效果表现较好，这与其研究成果相近。由于贝叶斯法综合了样本信息和先验信息，先验信息是统计推断不可或缺的重要因素之一，可来自历史文献或主观信念。其次，贝叶斯方法将样本和未知参数视为随机变量，具有一定的分布形式，而传统的统计学方法只是将未知参数看做为固定值[36]，综合以上贝叶斯方法的优势使得贝叶斯法在样本量较小时的估测精度要优于传统的统计法[37]。

2）贝叶斯模型其本身就具备层次性。而分层贝叶斯法由于加入了随机效应，使得整个模型具有更加明显的层次结构，同时也增加了模型的复杂程度，通过预测量中超参数随机效应与样本数据中固定效应结合，在小样本条件下，表现出极佳的估测精度。本研究选取的沧源县和新平县两个不同区域作为随机效应建立混合效应模型，利用分层贝叶斯方法拟合模型参数，通过引入随机效应，释放了区域间差异的约束，使其在不同条件下的差异更为显著[38]。

3）以往研究通过对树种单木水平的LAI测定，模型的研究可以取得较好的结果。但针对龙竹人工林单木水平的LAI难以获取，需综合考虑不同龄级，不同径阶对龙竹生长造成的影响，通过引入林分加权叶面积指数，可提高估测精度。

4）目前对叶面积指数的研究以遥感反演居多，对经验模型估测叶面积指数的研究较少。经验模型获取数据便捷，所需测树因子容易获取，但经验模型的经验性总体较强，对一些外界因子的限制考虑较少[39]，因此本研究使用贝叶斯法，对比传统经验模型，综合考虑了样本信息与先验信息，预测精度和可靠性得到进一步提升。但与遥感反演相比，其在较大尺度下表现却不尽人意。

本研究采用叶面积指数经验模型估测法，基于不同区域龙竹人工林加权叶面积指数数据，以传统统计法、贝叶斯方法和分层贝叶斯法为拟合方法拟合龙竹叶面积指数，最终得出基于分层贝叶斯法拟合得到的参数最佳。证实了当数据具有明显的区域差异或层次差异时，分层贝叶斯法可以显著提高龙竹人工林叶面积指数的估算效果。同时，发现以区域为随机效应和分层基础可显著提升估测精度。由于区域之间的地理位置，土壤养分条件的不同等因子会对林木的生长有影响，因此将区域作为随机效应能充分解释不同地区的叶面积指数的差异。下一阶段可对造成此差异的因素进行探究。