基于灰色关联分析综合法的信息系统安全管理评价

唐荣华

（广东金质信息技术有限公司，广东 广州 510220）

0 引 言

当前国际形势下，人们对信息安全越来越重视。没有信息安全就没有国家安全。因此，加强信息安全的管理以及对安全管理的评价也日趋重要。目前，对于信息安全管理的评估，许多专家学者结合评估指标，运用模糊数学、灰色理论、层次分析法（Analytic Hierarchy Process，AHP）、熵权理论等多种方法[1-4]，取得了不少研究成果，但仍存在一些不足。

（1）评价对象主要侧重于对信息安全和风险的评估，注重从全域的角度对软硬件环境、网络运行、应用、数据及管理等方面做安全评价，较少从管理角度进行评价。

（2）在评估方法上面，多倾向于模糊数学、灰色理论、AHP、熵权理论等方法的单独应用或简单组合。由于信息系统具有一定的复杂性和模糊性，评价往往带有较多的主观性，忽视了客观性和指标的相互影响等。

（3）在评价指标的选取上有较多的主观性，采用标准时也做了很多的裁剪，缺少权威性、普适性和客观性。

本文提出的基于灰色关联分析综合法的信息安全管理评价，评价对象是管理层面的评价，因为信息安全的重点在于管理，更多的是从上到下，没有上层的重视很难得到落实；在评价方法上，综合应用灰色系统理论的关联度分析、层次分析法多层递归综合和熵权理论等多种理论和方法，兼顾了指标属性的主观权重和客观权重，使评价更为科学；在评价指标的选取上，选择了国家标准《信息安全技术 信息系统安全管理要求》（GB/T 20269—2006）[5]中的全部指标，具有很好权威性和实用性。本方法针对性强，对系统等级安全保护的管理的改进具有非常重要的指导意义。

1 基于AHP的评价层级构建信息安全管理指标体系

国家标准《信息安全技术 信息系统安全管理要求》（GB/T 20269—2006）[5]对等级保护提出了具体安全管理要素及其在不同等级保护的执行强度，有利于对安全管理的评价。本文采用此标准对信息系统安全管理的要求，基于AHP的层次分析法建立如表1所示的信息系统安全管理指标体系。该体系分为目标层、准则层和指标层三层。目标层是信息系统安全管理，是评价的目标对象，准则层是8个影响因素，指标层是30个具体的属性指标。

表1 信息安全管理指标体系

2 信息安全管理评估模型

邓聚龙教授在1982年3月提出灰色系统理论[6]。它是根据序列曲线几何形状的相似程度来判断其联系是否紧密。形状越接近，对应序列之间的关联度就越大，反之就越小。本文指标体系分为三级，分别是目标层、准则层和指标层，结合主观权重和客观权重，先分别计算单个准则的指标关联度，然后再以各个准则的关联度结果作为输入，计算目标层的综合关联度。

2.1 运用AHP确定各级指标体系的主观权重

2.1.1 构建判断矩阵

利用AHP（层次分析法）[1]建立判断矩阵A=(aij)，满足其中，aij表示对上一层比较本层第i个指标和第j个指标的重要程度，其值通过专家打分来确定，分值采用1-9标度法，如表2所示。

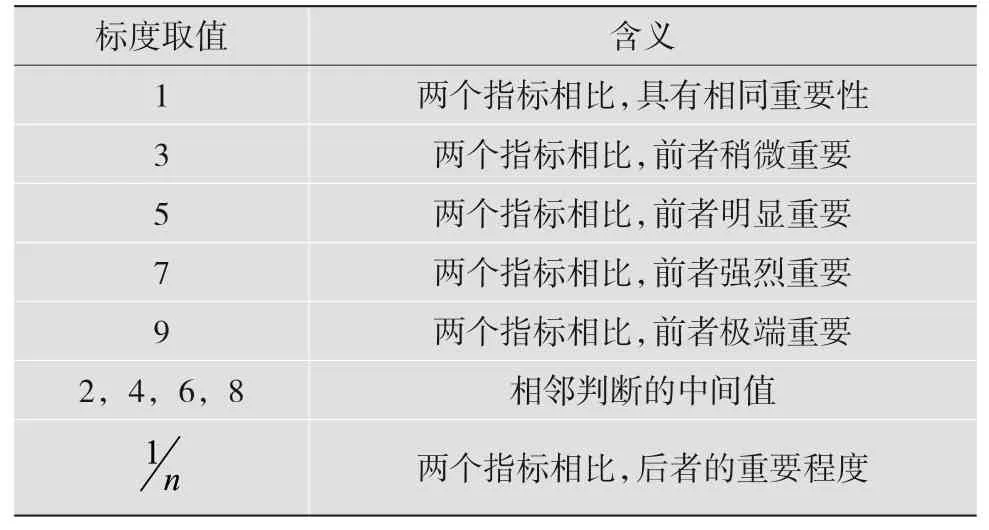
表2 层次分析1-9标度取值和含义

2.1.2 主观权重计算

根据信息安全管理指标体系层次关系，先计算指标层对准则层的权重，再计算准则层对目标层的权重。具体步骤如下。

（1）指标层对准则层的权重。对8个准则分别计算其下一层指标间的权重，每个准则的下一层指标构建判断矩阵A=(aij)n×n后，经过如下归一化和一致性评价，计算得出指标层因素对准则的主观权重向量WA(i)，(i=1,2,…,8)。

（2）归一化。先将判断矩阵每一列做归一化处理：

再对归一化后的矩阵每一行求和，并进行归一化处理：

得到向量WA即为相对权重。

（3）一致性检验。采用式（3）进行一致性校验：

式中：CI为一致性指标，其中λmax为判断矩阵的最大特征根；RI为平均随机一致性指标，一般当CR<0.1时，一致性可接受，否则需要重新进行专家打分。

（4）准则层对目标层的权重。用同样方法，准则层8个准则对目标层构建判断矩阵，经归一化和一致性评价，求得主观权重向量。

2.2 运用熵权法确定各级指标体系的客观权重

熵权法[3]是一种利用信息熵计算出各指标熵权的一种方法。它直接利用无量纲化后的矩阵所给出的信息计算出各指标的权重，而没有引入决策者的主观判断，是一种客观赋权方法。对于无量纲化后矩阵Xm×n（m个信息系统，n个指标），各指标的相对权重计算式为：

式中：Ej为第j个指标值的信息熵，j=1,2,…,n，其 计 算 公 式为若Pi(j)=0，则Ej=0。Pi(j)为计算第i个系统第j个指标值的比重，计算公式为

对相对权重进行归一化，即得到各指标的权重系数wB(j)：

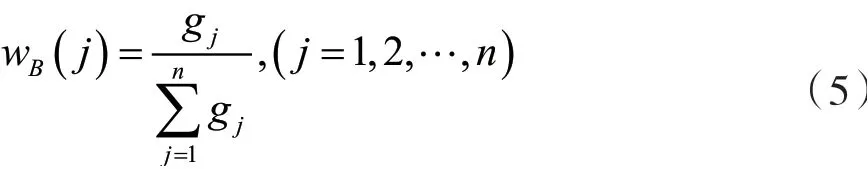
根据信息安全管理指标体系层次关系，先计算准则层各指标的权重，再计算目标层各准则的权重。

（1）准则层各指标的权重。对8个准则分别计算其下一层指标间的权重，每个准则的下一层指标无量纲化矩阵Xm×n（m个信息系统，n个指标）经相对权重公式（4）、式（5）求得客观权重wB(j)，(j=1,2,…,8)。

（2）目标层各准则的权重。以同样方法，目标层下一层8个准则构建无量纲化矩阵Xm×8，经相对权重式（4）、式（5）求得客观权重。

2.3 采集各信息系统评价构建初始矩阵

采集指标层各个指标的得分，按准则分别构建初始矩阵：

2.4 单准则关联度评价

2.4.1 无量纲化处理

对于单个准则指标值初始矩阵，指标得分越大越好。规范化采用以下公式进行无量纲化：

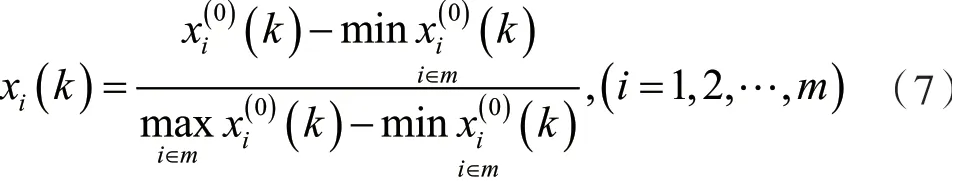
规范化变换后，式（6）变为

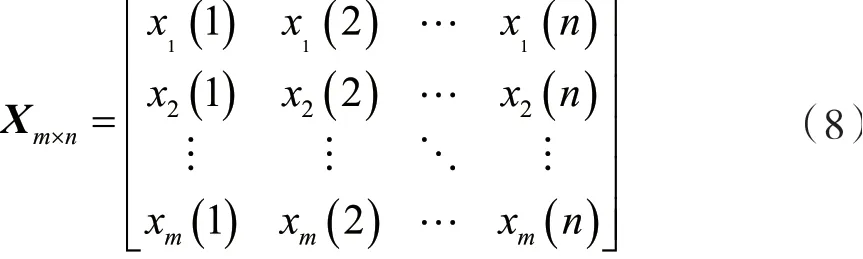
2.4.2 确定参考数列和比较数列

选取比较矩阵X中各项评估指标的最大值作为参考数列：

比较数列：

为第i个系统的比较数列。

2.4.3 建立关联系数矩阵

计算比较数列与参考数列的相对差值，定义如下关联系数计算公式：

式中：ρ为分辨系数，取值在0到1之间，一般取0.5，分 别表示|x0(k)-xi(k)|矩阵的最小值和最大值，式中ζi(k)为第i个系统的第k个影响因素对于参考系统x0的关联系数。

2.4.4 计算各影响属性的权重

采用客观的熵权法和带主观性的专家打分法对信息系统安全管理影响因素指标权重进行计算，分别得到影响因素指标k的权重系数：

式中：wA(k)和wB(k)分别为熵权法和专家打分法得到的权重，α为主观系数，0≤α≤1，通常取0.5。

2.4.5 计算灰色关联度

为了得到系统xi与x0的灰色关联度，需要将各影响因素的灰色关联系数进行加权求和求得灰色关联度向量，如式（13）所示：

2.5 综合关联度评价

先分别计算单个准则层准则的指标的关联度向量，然后把8个准则关联度向量合并作为初始矩阵计算目标层的关联度，方法同单准则关联度评价（1）-（5）的递归计算。

3 应用实例

本文以某集团公司10个信息系统的信息安全管理评价为例，分别以S1—S10表示10个系统，采集样本参数如下。

3.1 AHP确定各级指标体系的主观权重专家打分情况

指标层对准则层的权重判断矩阵：

准则层对目标层的判断矩阵：

3.2 按准则分别构建初始矩阵

通过对各信息系统的信息安全管理8个准则的指标进行打分（10分制），整理获得相应指标的评判情况，分别对8个准则构建8个初始矩阵。

3.2.1 主观权重和客观权重计算

根据采集的样本数据，运用式（1）—式（5）计算得各级指标的主观和客观权重，如表3所示。

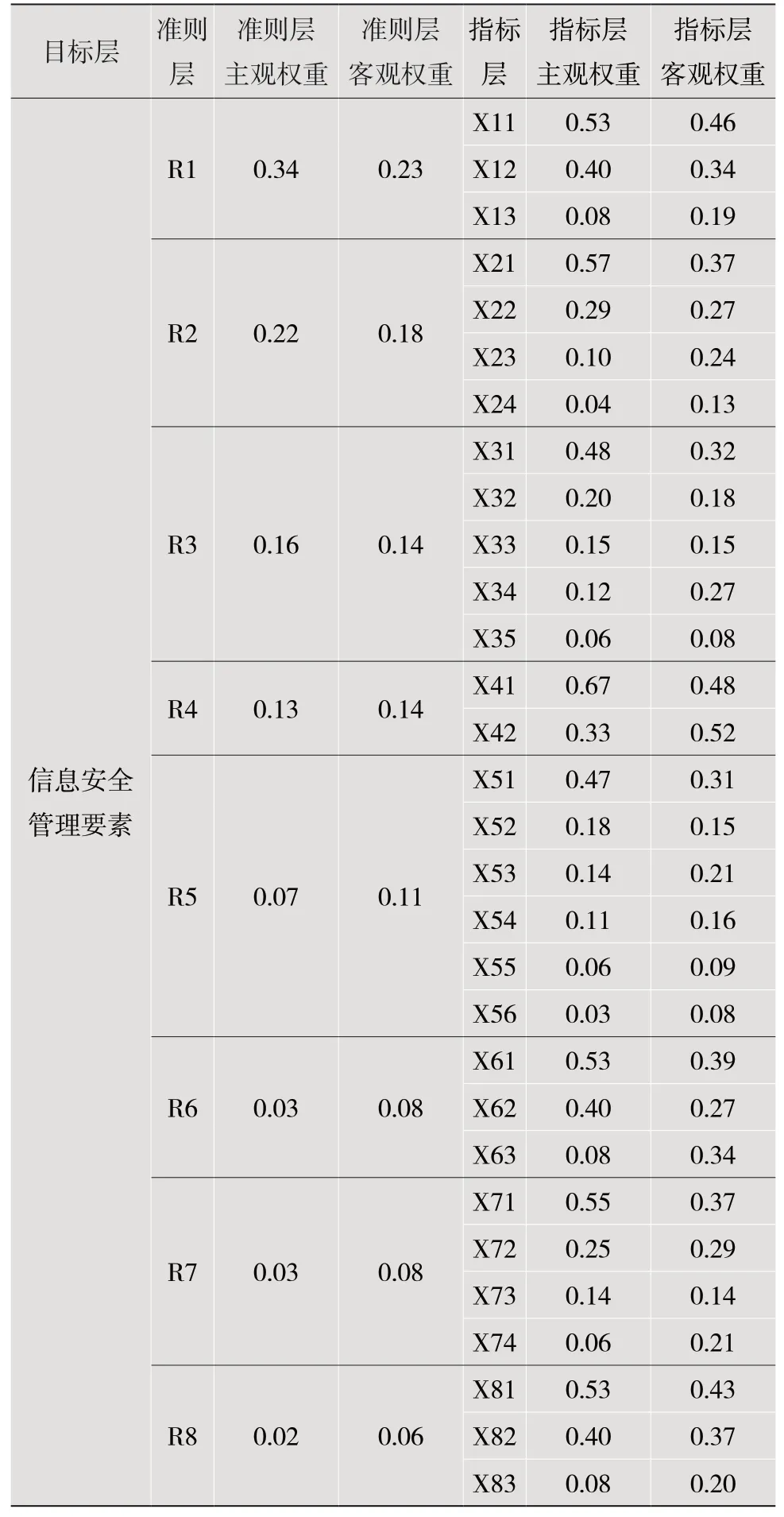
表3 各级指标的主观和客观权重

3.2.2 单项准则计算关联度

根据各准备采集的样本数据，经式（7）—式（13）计算各准则的关联度，结果如表4所示。

3.2.3 综合评价

以表4各单项准则关联度为初始矩阵X0，结合准则层的主观权重和客观权重，经单项准则计算关联中（1）-（5）计算得出如下综合评价关联度：[0.91 0.47 0.40 0.51 0.55 0.47 0.50 0.49 0.58 0.65]T。把综合的评价关联度和8个准则的关联度合并并排序，得到表5的结果。

表4 各单项准则关联度

由表5可以得到10个信息系统的评价结果。综合评价得分最高的是S1号信息系统，管理能力最优；得分最低的是S6号，管理能力有待进一步提高。根据综合关联度的高低，可以确定总体排名情况。根据单项准备的关联度高低，也可以找到在哪些指标和准则存在不足，从而采取有针对性的改进措施，有效提升管理能力。

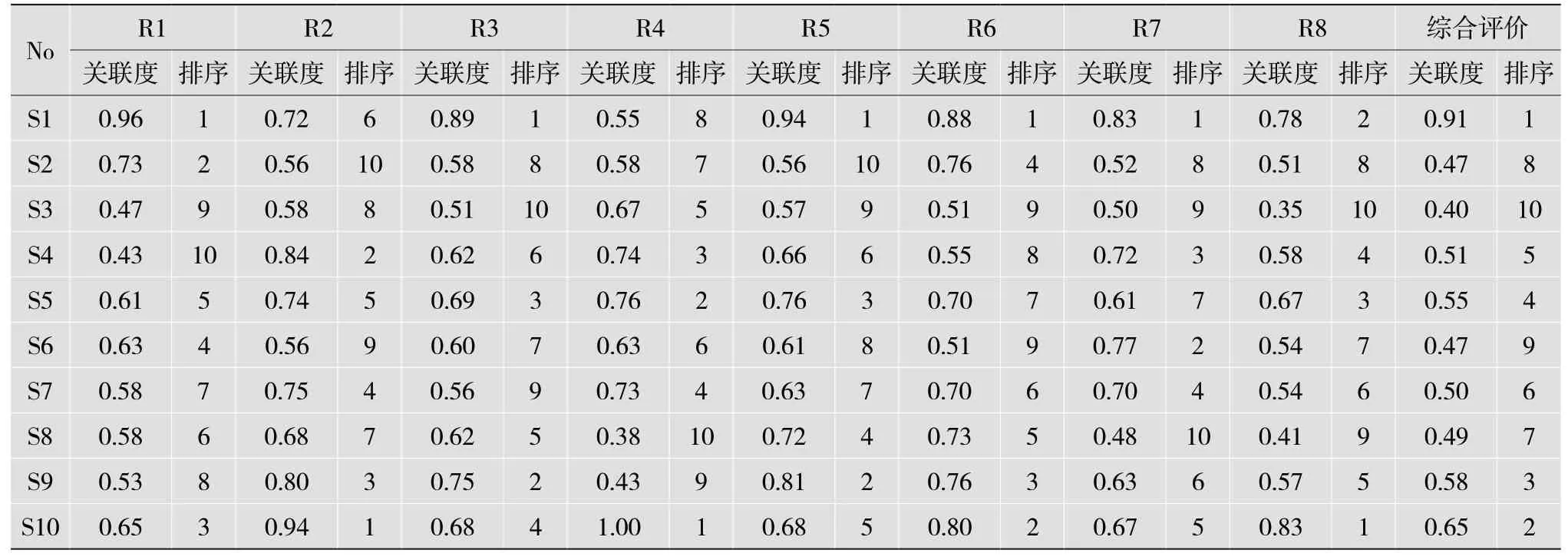
表5 各单项准则关联度和综合评价排序表

4 结 语

本文针对信息安全管理评价存在的问题，首先采用国家标准基于AHP的评价层级构建信息安全管理指标体系，然后借助灰色理论、层次分析法和熵权法论述了信息安全管理评估模型的综合评估建模过程，最后通过实例完成了对某集团公司10个信息系统的信息安全管理评价，具有以下创新点。

（1）从管理层面进行评价，抓住管理层面这个关键要素，有利于对管理人员的绩效考核和信息安全的推动和落地。

（2）从目标、准则和指标三个层次，先分层、分准则进行灰色关联度分析，再综合递归计算，自下而上，简化了问题处理复杂度，避免了同一层指标过多时指标权重的设置困难。

（3）采用AHP专家打分确定各级指标体系的主观权重和熵权法确定各级指标体系的客观权重相结合的方法，克服了评价中的主观偏差。

（4）选用与等级保护相关的国家标准作为评价指标体系，保证了评价指标的权威性和实用性问题。