基于遗传算法的域间路由系统跳变链路生成

王 禹，王银川，焦飒镧，张劳模

(1.河南工程学院 软件学院，河南 郑州451191; 2.中国移动通信集团郑州分公司 网络部，河南 郑州 450000)

边界网关协议(border gateway protocol，BGP)是目前互联网上唯一部署的域间路由协议，它负责自治域(autonomous system，AS)之间交换网络可达性信息(network reachability information, NRI)，属于增量路径向量协议，可避免发生路由循环。BGP依赖于自治域之间的相互信任，极易受到错误配置、路由劫持和拒绝服务等攻击[1-2]，以致影响互联网正常通信。因此，BGP运行的安全性和稳定性对于全球网络至关重要。

考虑到日益增多的域间路由系统攻击，其突发性和扩散性对路由系统的应急响应能力提出了更高的要求。Cheng等[3]提出了多项式时间的启发算法来计算自治域之间的稳定路径；Damanik[4]为实现对路由系统不同级别的复杂失效路由进行建模，提出了多路径快速恢复和优化方法；Tran等[5]针对路由拥塞防御可行性进行深入分析，提出了实用性很强的重路由方案。但是，已有研究大多忽略了多节点资源/策略整合问题，且只着眼于实时性或近实时性操作，难以满足多域资源调配复杂性下重路由或恢复路由时间紧迫程度的需求。

本研究提出构建多域社团，利用预计算多路径跳变机制，基于遗传算法生成跳变候选集，从而应对多自治域的路由系统通信失效场景。其本质是预先为多域社团节点对(nodes pair)计算尽可能完备的不相交路径集合，在多域中心控制器负载受限时立即随机选取不同转发路径以实现跳变，进而实现通信可达的目标。

1 多域社团

域间路由系统在AS级拓扑结构上存在典型的社团特性，主要表现如下：社团内部各组织联系紧密，社团外部联系松散；社团内AS节点的地理位置靠近；社团内AS节点通常具有较为一致的利益关系。基于此，旨在更好地应对域间路由系统攻击，尤其是BGP-LDoS对于拓扑关系的探测，本研究给出一种轻量级的协作防御模式，根据地理位置和权益关系将域间路由系统中已经具备典型社团特征的多个自治系统，构建为共同面向域间路由安全的多自治系统社团。

假定编号为1～10的自治域拥有共同的通信、利益诉求且相互毗邻，具备基本的社团特征，则可将其组织为多域社团，如图1所示。该社团边界的4个自治域编号分别为1、2、8、9，同社团外部连接的自治域包括A、B、C、D和E等。

图1 多自治域社团

2 数据结构定义

结合域间路由系统结构特性，进行数据结构的定义。

2.1 节点的定义

对于单个自治域节点，定义“节点状态信息”，用于体现该节点的即时状态，格式为

"ASN":(bandwidth, AS_class, reachability, longitude, latitude)。

其中，ASN表示该节点全球唯一的自治域号码，bandwidth为当前出口带宽的最小值，AS_class为自治域类型，reachability表示节点此时的可达性，longitude和latitude分别代表该自治域所处区域中心的经度和纬度。

多个自治域节点组成的nodes集合形式如下：

nodes ={′13335′:[1 024, ′Transit′, 1, ′4.881′, ′89.2343′], ′8888′:[1 024, ′Transit′, 1, ′8.888′, ′88.888′], ′1111′:[1 024, ′Stub′, 1, ′4.881′, ′89.2343′],…}。

2.2 边的定义

两个毗邻的自治域节点连接组成一条边(edge)，形式为"ASN-ASN"。多条边组成edges集合，形式如下：

edges = {′13335-18403′: 2 048, ′56149-18403′: 2 048, ′24088-55309′: 2 048, ′1111-8888′: 2 048, ′45899-45903′: 2 048,…}。

在定义了节点与节点集合、边与边集合之后，对国家/地区AS级自治域链路信息进行提取。

2.3 链路的定义

可使用多个自治域节点来表示一条双向链路，例如某条链路以列表为类型，可表示为如下形式：

link =[′18403′, ′18403′, ′56149′, ′55309′, ′24088′, ′45903′]。

在此基础上，由多条链路共同组成链路集合，例如：

links =[′18403′, ′18403′, ′56149′, ′55309′, ′24088′, ′45903′],[′18403′, ′13335′, ′56149′, ′55309′, ′24088′, ′45903′], …]。

3 恢复链路生成方法

遗传算法是一种用于计算的搜索过程，用于寻找问题的精确解或近似解，也被称为全局搜索启发法。基于遗传算法的恢复链路生成(genetic algorithm based recovery link generation,GARLG)方法，主要包括链路提纯、链路有效性检验、链路适应度计算、链路遗传概率计算、父体染色体和母体染色体选择、变异计算和染色体交叉等子算法。

3.1 链路提纯

定义link_refine，对链路实施提纯，依次判断该链路中的每个AS节点，如果发现某节点为NA，即该节点位于当前考察区域之外，则舍弃该链路；此外，将重复出现的节点予以去重操作。

例如，待检验链路为[′18403′, ′13335′, ′13335′, ′56149′, ′55309′, ′24088′, ′24088′,′45903′]，去重后为[′18403′, ′13335′, ′56149′, ′55309′, ′24088′, ′45903′]。

3.2 链路有效性检验

定义is_valid_link方法，用于判断某条链路是否有效，需要结合nodes和edges数据集进行判断。

①针对该链路中的所有节点，判断其是否存在于nodes集合，以及reachability是否符合条件(reachability为1则表示可达)，从而认定其是否存活。②针对链路中涉及的各个边，依次判断其是否存在于edges集合，从而认定该链路是否保持连接；如果有任何一段边存在于edges集合之外，则表明该链路无效。上述两步若均满足，则判定该链路为有效链路。

3.3 计算链路适应度

适应度(fitness)函数也称评价函数，是根据目标函数确定的用于区分群体中个体好坏的标准。适应度函数总是非负的，而目标函数可能有正有负，故需要在目标函数与适应度函数之间进行变换。

基于前述的link_refine和is_valid_link，定义get_fitness来计算链路集合pop中的全部有效链路及其对应的fitness值。过程如下：首先从pop集合中筛选出有效路径，然后比对该链路中每条边的带宽，从而获得其最小带宽值，作为该链路的fitness值。例如，[((′55315′, ′7552′, ′55308′), 2 048),((′135947′, ′38731′, ′63734′), 2 048)]分别表示两条链路及其fitness值。

3.4 计算链路遗传概率

根据每条链路的fitness值，计算出每一个体被遗传到下一代群体中的概率

(1)

式中：p(xi)表示第i条链路遗传至下一代的概率；xi表示链路群体中第i条链路；f(xi)表示第i条链路的fitness值。

以转盘划分(图2)为例，链路群体的每一条链路可视为一个染色体，每个染色体的fitness值(即遗传概率)对应饼图中一小块，fitness值越高，则饼图中小块所占面积越大。

图2 轮盘划分

遗传算法中，轮盘赌选择又称比例选择，运用该算法的目标是选取一个染色体。转动轮盘，观察轮盘停止时指针停在哪一块区域，则选中与它对应的那个染色体。由此可知，每个个体被选中的概率与其fitness值成正比。按照上节fitness的定义可知，链路被选中的概率与其带宽成正比，带宽越大，链路越容易被选中。

3.5 选择父体/母体染色体

利用累积概率和轮盘赌算法，分别计算选择父体染色体和母体染色体，要求二者相异。轮盘旋转停止后，需要判断指针落于哪个区域，采用累计概率(cumulative probability)的计算方式进行选择判断。每条染色体的累计概率

(2)

染色体遗传概率的取值为0～1，将其依次进行排列，计算得到累计概率值。若qi大于当前轮盘指针的数值，则染色体i被选中(即第i条链路)；若qi小于当前轮盘指针的数值，则比较下一个染色体qi+1，直至选出符合的个体为止。

3.6 变异操作

遗传算法中的变异(mutation)运算[6]，是指将个体染色体编码串中的某些基因座上的基因值用该基因座上的其他等位基因来替换，从而形成新的个体，包括基本位变异、均匀变异、边界变异、非均匀变异和高斯近似变异等。针对染色体可能出现的变异特性，引入基本位变异操作。当设置的变异发生概率(较小概率)小于该阈值时，可以随机实施链路中AS节点删除操作，或者链路中两个AS节点的交换操作，增加链路突变优化的可能性。

3.7 染色体交叉

遗传算法的交叉(crossover)运算，是指对两个相互配对的染色体按某种方式相互交换其部分基因，从而形成两个新的个体。常见的交叉算子包括：单点交叉(one-point crossover)，指在个体编码串中只随机设置一个交叉点，然后在该点相互交换两个配对个体的部分染色体；两点交叉(two-point crossover)，指在个体编码串中随机设置两个交叉点，然后再进行部分基因交换；均匀交叉(uniform crossover)，也称一致交叉，指两个配对个体每个基因座上的基因都以相同的交叉率进行交换，从而形成两个新个体；算术交叉(arithmetic crossover)，指由两个个体的线性组合而产生出两个新个体，该操作对象一般是由浮点数编码表示的个体。本研究采用单点交叉方式，当满足随机数小于设定的交叉率CROSSOVER_RATE时，利用轮盘赌算法从种群中选择出父体染色体和母体染色体，并随机产生交叉点位，完成染色体链路的交叉。如果新链路能够通过有效性检验，则将其加入种群中。随着多轮交叉与变异，种群不断扩展，性能更优的链路将存在于种群之中，保证恢复链路。

4 实验

仿真实验的数据来源于应用互联网数据分析中心(center for applied Internet data analysis，CAIDA)2020年发布的互联网拓扑数据集(Internet topology data kit，ITDK)[7]，该数据集由基于Ark(archipelago)推导获得的traceroutes命令生成。首先分别实施了功能与性能实验，针对西欧相互毗邻的部分国家，抽取其ASN、地理位置、链路等自治域节点信息，如表1所示。验证过程共400轮，依照不同的初始种群规模、变异率、交叉率、生成链路数目的组合进行，然后对比已有典型跳变算法并分析其优劣。

表1 自治域节点信息

4.1 功能实验

针对所提方法，一方面需要验证链路生成的有效性，另一方面需要注意约束性节点的可控性。验证过程中391轮完成恢复链路计算任务，正确率达97.8%左右。图3和图4展示了以ASN 205996为起点、以ASN 16313为终点的链路生成实验结果。

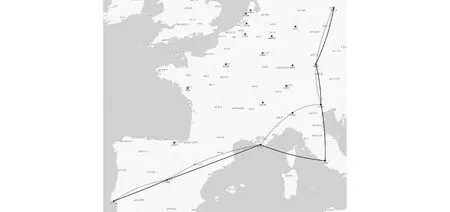
图3 预计算生成2条最佳路径

图4 预计算生成5条最佳路径

假定ASN 60768遭受BGP-LDoS已失效，则经过所提遗传算法的计算，在已有种群基础上新生成的链路符合恢复路径的需求，其中设置了约束性排除节点ASN 60768。以预计算生成两条最佳路径为例，Path1为[′205996′, ′31428′, ′200804′, ′57495′, ′31167′, ′12605′, ′16313′]，Path2为[′205996′, ′31428′, ′200804′, ′20958′, ′31167′, ′12605′, ′16313′]，见图3。

以预计算生成5条最佳路径为例，同样设置了约束性排除节点ASN 60768，依照不同线型和灰度可得5条路径，即Path1为[′205996′, ′31428′, ′200804′, ′57495′, ′31167′, ′12605′, ′16313′]，Path2为[′205996′, ′31428′, ′200804′, ′20958′, ′31167′, ′12605′, ′16313′]，Path3为[′205996′, ′10429′, ′200804′, ′57495′, ′31167′, ′12605′, ′16313′]，Path4为[′205996′, ′10429′, ′200804′, ′20958′, ′31167′, ′12605′, ′16313′]，Path5为[′205996′, ′10429′, ′2856′, ′45758′, ′29686′, ′8839′, ′16313′]，见图4。

4.2 性能实验

本阶段实验方案包含两项。

其一，在相异参数配置下，分别生成满足规范条件的最优链路候选集。假定不同情况下候选集合中链路数目均相同(以生成2条恢复链路为目标)，比对生成候选链路所需要的迭代次数。遗传算法中变异率一般取值较小，则针对初始种群数目、变异率、交叉率的4类配置如下：

A参数配置：初始种群为40，变异率为0.05，交叉率为0.90。

B参数配置：初始种群为60，变异率为0.05，交叉率为0.90。

C参数配置：初始种群为60，变异率为0.08，交叉率为0.95。

D参数配置：初始种群为90，变异率为0.08，交叉率为0.95。

图5展示了不同参数配置下的迭代次数，可知在初始种群数量相同时，变异率和交叉率阈值较高时所需迭代次数相对较少，即具有更好的生成性能；在交叉率和变异率保持一致时，初始种群数量越大越有利于发现最优路径，缩短生成时长。

图5 不同配置类型下候选集生成迭代次数

其二，在相同参数配置下，以B参数配置为模板，生成满足规范条件的最优链路候选集，根据目标链路数目的不同，比较生成迭代次数。图6为不同链路数目下候选集生成迭代次数，可知在目标链路数目分别为2、4、6和8时，迭代次数依次呈递增态势分布，且增长幅度不断降低。考虑到种群的不断优化，所以符合需求的链路能够得以更快地被发掘。

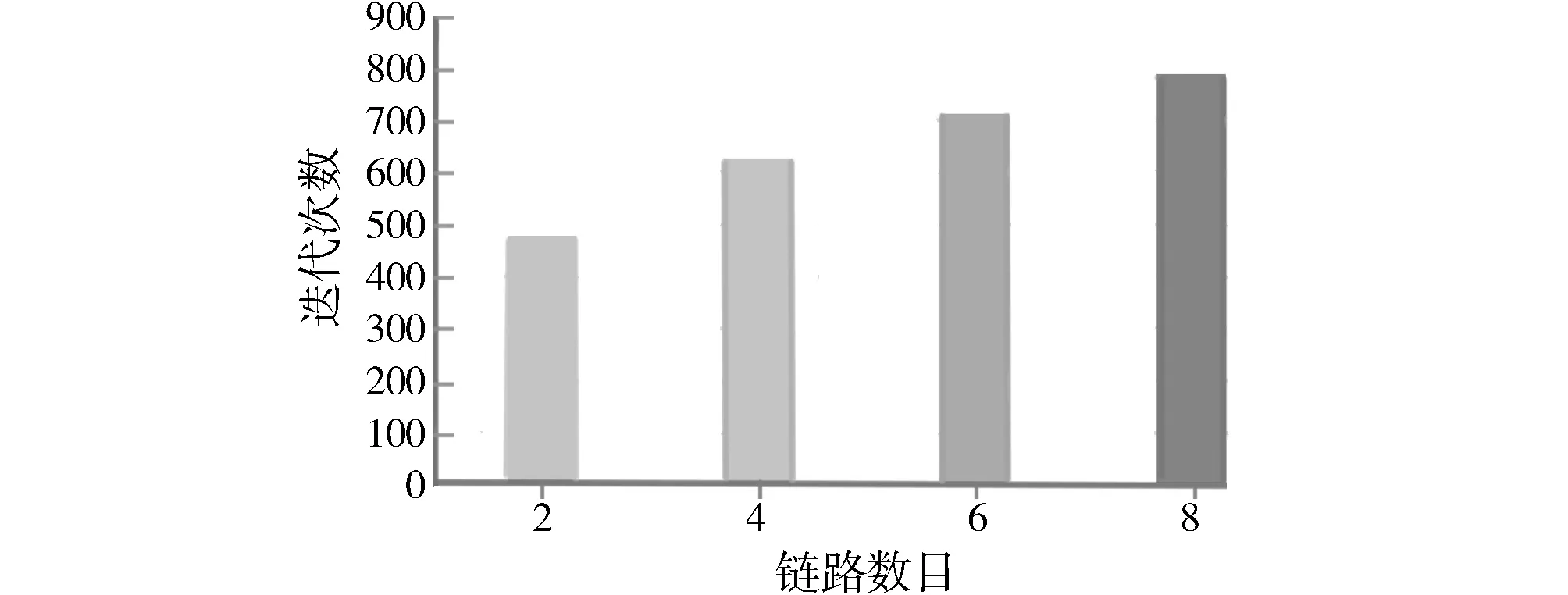
图6 不同链路数目下候选集生成迭代次数

4.3 对比实验

跳变是主动防御技术的核心技术之一，张连成等[8]提出了一种基于路径跳变的算法，即PPAH-SPD算法，该算法可随机改变通信双方之间的通信路径与路由。以前述网络拓扑结构为基准，将本算法与PPAH-SPD算法进行比较。

实验硬件配置如下：CPU为Intel(R)Core(TM)i7-10750H，2.60 GHz，内存16 G。针对不同跳变路径长度，计算二者时间消耗情况。其中，本算法采用了前述的C参数配置，即初始种群为60、变异率为0.08、交叉率为0.95。两类算法的生成时长对比见图7。

图7 两类算法的生成时长对比

由图7可知，当路径长度均为3时，二者计算时长基本相当，PPAH-SPD算法略优；随着路径长度的增加，两类算法的时长都不断提高，但本算法的增长态势优于PPAH-SPD算法。可以看到，当恢复路径长度为6时，二者的时长差距为70 ms左右，由此可知随着路径长度的扩展，本算法计算复杂度的优势将更为显著。

5 结语

在针对互联网实际自治域拓扑的仿真实验中，通过不断优化得到了最优交叉率和变异率，所提算法能够设置约束排除节点，预计算生成多路径跳变集合，满足路径数目、跳数及带宽需求。对算法进行功能和性能测算，并与已有典型算法对比，证明了本算法的有效性。