某重型燃机涡轮盘连接优化设计及焊接变形影响分析
权立宝
(中国航发燃气轮机有限公司)
0 引言
涡轮盘作为燃气轮机关键部件之一,叶片与轮盘质量及转速引起的离心力、温度梯度产生的热应力以及相关零件非协调变形的附加应力是其受到的典型载荷[1,2]。离心载荷和温度载荷的不同步,轮盘复杂几何导致的应力不均匀和梯度,是其典型的载荷分布特征,且轮盘的工作环境非常恶劣[3],使其受载情况更加复杂。轮盘工作时一旦破坏,往往造成无法挽回的灾难性损失。因此,轮盘的设计必须考虑材料、强度、振动、寿命以及加工工艺性等问题,尽可能地提升轮盘的可靠性。
在实际工程应用中,常采用有限元方法对轮盘机组的强度进行计算和校核。袁定军等[4]通过有限元分析软件对某机型飞轮强度进行了计算,讨论了飞轮的强度及热应力,为飞轮的结构优化提供有效的依据。童正明等[5]针对涡轮增压器离心压气机叶轮轮盘边缘断裂故障,建立压气机三维模型,进行有限元强度分析和有限元模态分析。张同桐等[6]分析了在实际工况下叶轮表面的von-Mises应力分布,发现在叶片进口边,尤其是叶顶和叶根位置应力最大。为了减小叶轮局部位置上最大von-Mises应力,分别对叶片与轮盘、轮盖的连接处倒圆进行了分析。赵明等[7]为了分析某烟机轮盘在受损修复后的使用寿命,采用有限元方法对该轮盘在修复前后不同工作状态下的强度和寿命进行了分析比较,给出了修复后轮盘安全系数和工作寿命的变化,确定修复后轮盘的安全系数。上述研究多数研究了轮盘本身的结构强度,而针对连接点对轮盘强度的影响却鲜有人分析。
针对某型燃气轮机的轮盘焊接连接结构对整体强度的影响,本文采用某型轮盘组件的循环对称模型,基于有限元方法分析对轮盘的整体强度进行分析,并优化了连接结构,分析了不同连接条件下的轮盘等效应力和应力储备系数。
1 研究目标与对象
1.1 研究目标
对某国产重型燃气轮机第一级涡轮盘结构进行强度计算,与焊接变形结构的强度校核结果进行对比分析,获得焊接变形对涡轮盘的影响。此外,为彻底解决焊接造成轮盘的变形翘曲,提高涡轮盘的可靠性,开展第一级涡轮盘连接结构的优化设计与可靠性评估。
1.2 研究对象
某国产重型燃气轮机涡轮转子是一种盘鼓混合式结构,本文研究对象为该型燃气轮机的第一级涡轮盘组件,由吊挂盘、鼓筒及第一级涡轮盘组成,采用电子束焊接方式连接成一体,其具体结构如图1所示。焊接后的应力释放造成轮盘辐板翘曲变形,而第一级轮盘组件中间为半封闭环腔结构,无法通过机械加工保留余量的方式保证轮盘中心对称和各截面的壁厚要求,从而可能影响轮盘组件的强度与运行安全性,因此需要对轮盘组件的焊接变形结构的强度进行校核,必要时应对其结构进行优化设计。轮盘材料均采用的是GH2674高温合金,轮盘运行时的环境温度250℃,该温度下的材料性能数据见表1。

图1 第一级涡轮盘组件三维模型Fig.1 Three dimensional model of the first stage turbine disc

表1 GH2674高温合金材料参数(250℃)[8]Tab.1 Material parameters of GH2674 superalloy(250 ℃)
1.3 计算方法及流程
本文考虑轮盘组件为循环对称结构,选取1/82 扇区作为计算对象,采用AnsysWorkbench 商业有限元软件计算轮盘组件的强度结果。轮盘组件有限元计算的主要流程如图2所示。首先,将轮盘组件的模型切分出1/82扇区,并将其导入Workbench定义轮盘组件的材料参数;然后对叶片的质量进行等效,在模型的叶片质心位置建立叶片等效质量点,在轮盘组件的切分截面设置循环对称边界;其次,对轮盘组件模型进行网格划分,并检查网格单元的质量;最后,根据轮盘组件的运转环境设置边界条件和载荷,完成数值计算并得出响应的强度和变形结果。

图2 轮盘组件有限元计算流程Fig.2 Finite element calculation process of wheel disc assembly
2 计算模型和载荷
2.1 边界条件
为了更准确地模拟分析对象的边界条件,得到更为精准的强度校核结果,需要进行边界条件的确定。首先,分别将连接一级盘和二级盘的转接环、连接吊挂盘及其负载的转接环以及连接吊挂盘和第一级涡轮盘的盘心圆柱壳体考虑到计算模型中,具体考虑方式如图3(a)所示。然后,对重组结构两端分别施加载荷和约束条件:在图3(b)中A 位置设置轴向和周向位移约束;B位置施加扭转载荷。

图3 一级盘及转接环两端边界条件设定方案Fig.3 Setting scheme of boundary conditions at both ends of primary disc and adapter ring
2.2 模型的选择
为了实现模型减缩以提高模型计算效率,本研究将采用循环对称算法,因此将全尺寸模型减缩为原模型的1/82个扇区。计算模型网格尺寸为2.5mm,单元类型为Solid186,共包含75672 个单元、348852 个节点,具体计算模型网格划分效果如图4所示。

图4 分析对象的网格划分结果Fig.4 Meshing results of the analysis object
2.3 载荷的施加
本文的分析对象为吊挂盘、转接环及一级涡轮盘组成的整体结构,工作载荷包括轮盘自身质量、叶片质量和转速产生的离心载荷、温度载荷以及扭矩载荷,运行转速为3000r/min,不同部件处功率载荷如表2 所示,转换为扭矩载荷见表3。
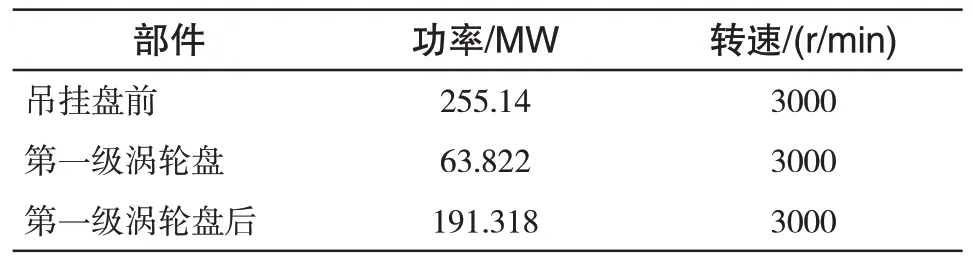
表2 不同部件处功率载荷Tab.2 Power loads at different parts

表3 不同部件处扭矩载荷Tab.3 Torque loads at different parts
为了模拟真实载荷条件,施加载荷的具体方案如下:第一,对轮盘组件结构中一级涡轮盘后转接环端面施加扭矩载荷;第二,通过透平功率换算出每个叶片承载的周向载荷,并施加在叶片质心位置,如图5所示。

图5 叶片周向载荷施加位置Fig.5 Application position of blade circumferential load
3 强度计算和校核
通过计算得出变形前与变形后的吊挂盘、转接环及一级涡轮盘的等效应力、径向应力及周向应力云图,如图7 及图8 所示,表4 中提供了原设计与变形后轮盘分析结果,并计算得到单点储备应力系数,其具体公式如下:
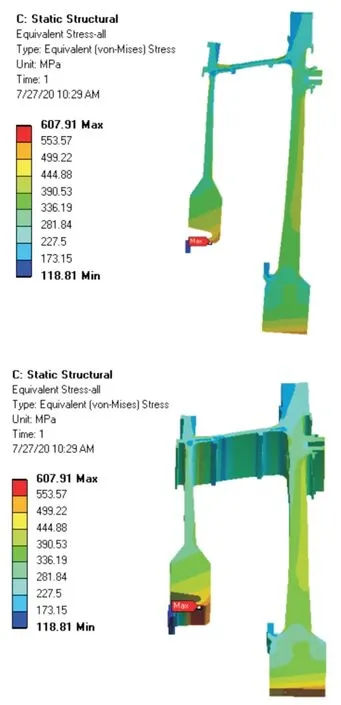
图7 原设计结构轮盘整体结构等效应力云图Fig.7 Equivalent stress for the overall structure of the wheel disc of the original design structure
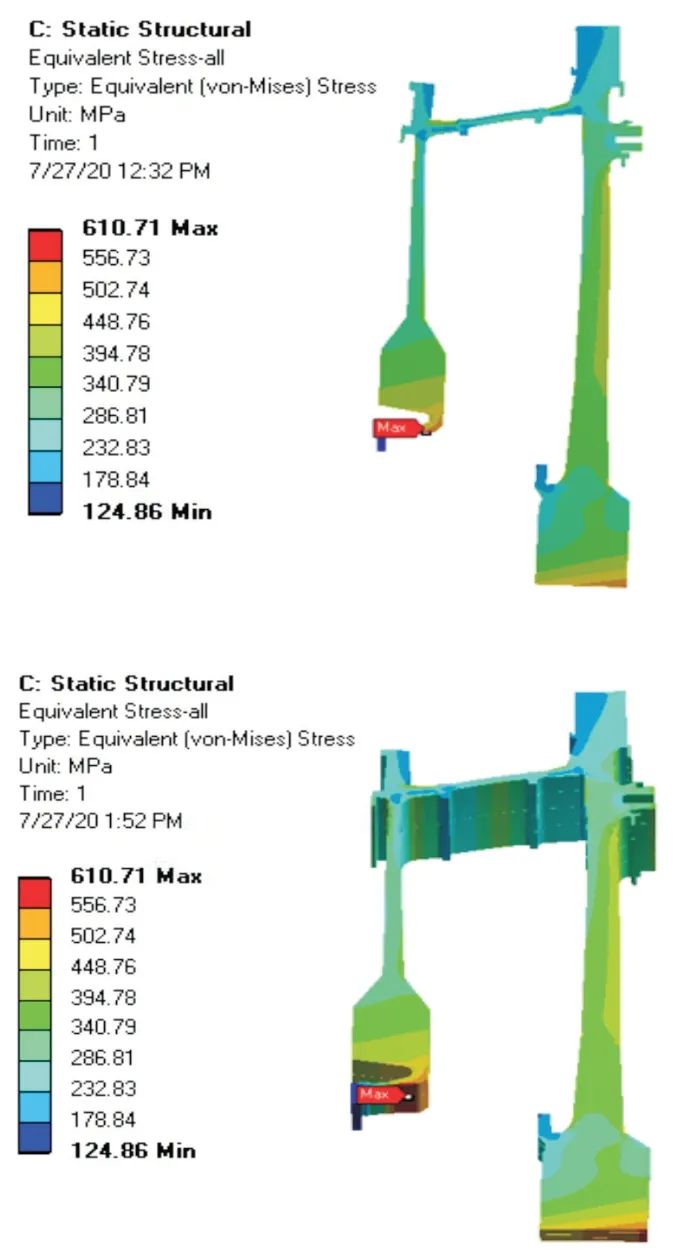
图8 焊接变形后轮盘整体结构等效应力云图Fig.8 Equivalent stress on the overall structure of wheel disc after welding deformation
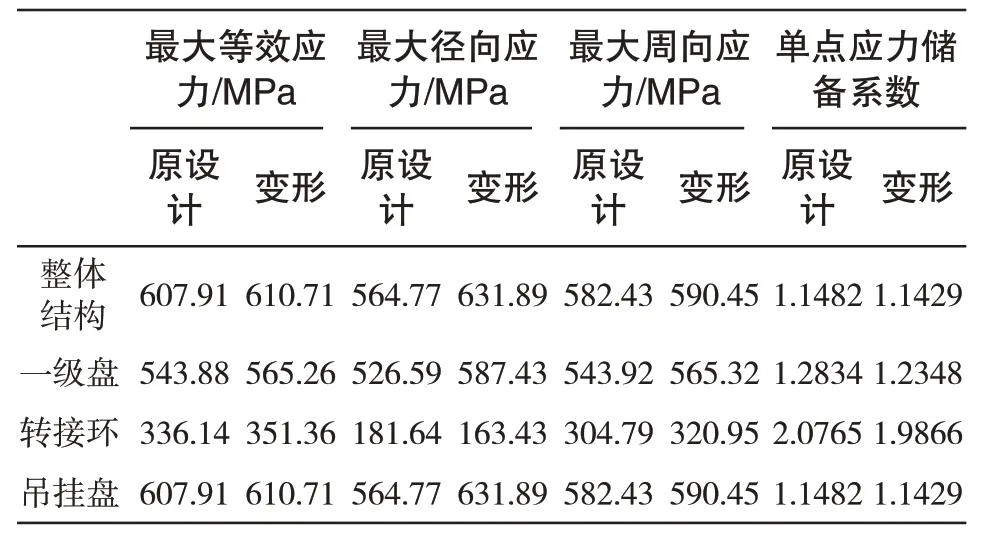
表4 原设计及焊接变形两种状态的等效应力、径向应力及周向应力云图计算结果Tab.4 Cloud chart calculation results of equivalent stress,radial stress and circumferential stress in original design and welding deformation

式中,σ0.2是材料的屈服极限,本次计算使用的合金GH2674环境温度250℃下的屈服极限应力698MPa;σE为单点节点等效应力;i为节点编号。
4 优化结构的强度校核与传扭可靠性分析
4.1 轮盘组件结构优化
因每一台轮盘的焊接变形翘曲的大小和位置不可控,导致涡轮盘的应力分布存在差异,给燃气轮机的安全可靠性带来不确定性。为解决焊接造成的变形影响,开展了第一级涡轮盘组件连接结构优化设计,优化后的结构见图9。

图9 优化后的轮盘结构Fig.9 Optimized wheel-disc structure
具体优化内容为:
1)转接环与第一级涡轮盘仍采用电子束焊接连接;
2)吊挂盘与转接环采用精密螺栓连接。
该种连接方式将原来的半封闭环形结构转变为开式环形结构,这种连接结构的优点在于可通过焊接后组合加工的方式消除焊接引起的变形,保证了零件与设计状态的一致性和可控性。为满足第一级涡轮盘组件安全稳定运行的要求,开展优化结构的强度校核和传扭可靠性分析。
本节分析中轮盘材料与第1节内容相同,结构优化新增加的螺栓采用M20×1.5型螺栓,材料采用GH4033高温合金,结构运行的环境温度为250℃,该温度下的材料参数如表5所示。

表5 GH4033合金材料参数[3]Tab.5 Alloy material parameters of GH4033
4.2 载荷条件
施加在改进设计方案结构上的载荷有两种:
1)第一种载荷与2.3节内容所施加的载荷相同;
2)第二种载荷则是施加在螺栓上的预紧力,预紧力为内载荷,根据螺栓的材料属性及标准进行螺栓预紧力测算。
在装配过程中,通过拧紧力矩控制预紧力,优化结构中螺栓施加拧紧力矩300/(N·m),根据《机械设计手册》第四版第二卷(成大先主编)[9],可得螺栓预紧力为88888.9N。
4.3 有限元建模
对传扭可靠性进行分析和结构强度计算及校核前,需要对模型进行网格划分,并施加边界条件及载荷,以求得接触界面的法向压力和结构强度。根据螺栓分布特征,采用循环对称算法,根据周向螺栓数量将全尺寸模型减缩为原模型的1/100 个扇区。计算模型局部网格尺寸细化,具体计算模型如图10所示。

图10 循优化结构的环对称模型网格划分结果Fig.10 Meshing of model based on optimized structure
4.4 传扭可靠性分析
在工作过程中,螺栓连接结合面通过摩擦传扭,承受转矩T的作用,螺栓连接界面有平衡方程:

经计算,螺栓连接部位各接触界面法向压力为N0=1.3907×105N。为实现较高传扭可靠性,连接界面应该不发生相对移动,根据《机械设计手册》第四版第二卷(成大先主编),最大可传递扭矩为:

式中,N0为连接界面压力;Kn为可靠性系数,通常为1.2~1.5,取值1.5;r为螺栓处旋转半径,r=0.915m;μ为摩擦系数,为0.1~0.16,取0.135;z为螺栓数量,取100。
本文研究对象在运行过程中不同位置处扭矩载荷如2.3节表3所示。对比发现,Tmax>8.124×105N·m。计算结果表明,能够传递的最大扭矩大于实际工作扭矩,能够实现摩擦传扭(若摩擦系数μ=0.1,经计算预紧力F0=120000N,接触界面法向压力N0=1.7714×105N,Tmax=1.0805×106N·m>8.124×105N·m,仍然能够实现摩擦传扭)。
4.5 结构强度计算及校核
本节载荷条件的施加除螺栓预紧力外均与2.3节内容一致,通过计算得出轮盘应力云图,如图11所示。计算结果显示,最大等效应力出现在转接环圆角处,最大径向应力出现在吊挂盘靠近螺栓连接处,最大周向应力出现在吊挂盘吊耳处。
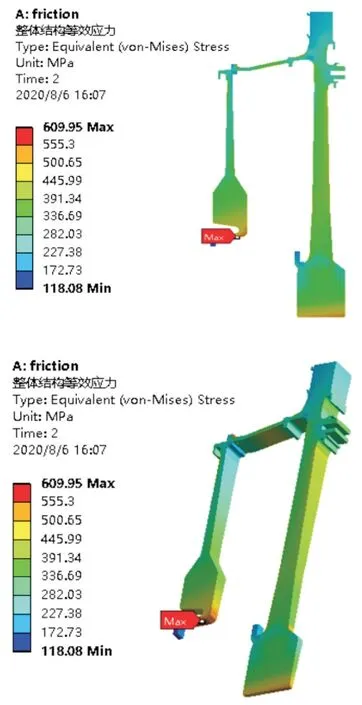
图11 采用螺栓连接轮盘整体结构等效应力云图Fig.11 Equivalent stress of the turbine disc connected by bolts
为了更加清楚地对比原结构和改进后螺栓连接结构的应力情况,这里将原设计与优化设计结构的最大等效应力、最大径向应力及最大周向应力列出,如表6 所示。结果表明:尽管转接环处等效应力有一定增加,但远低于其屈服极限;关键结构件精密螺栓连接结构一级盘最大等效应力变化不明显;整体上单点应力储备系数变化不大,足以保证设备稳定运行。
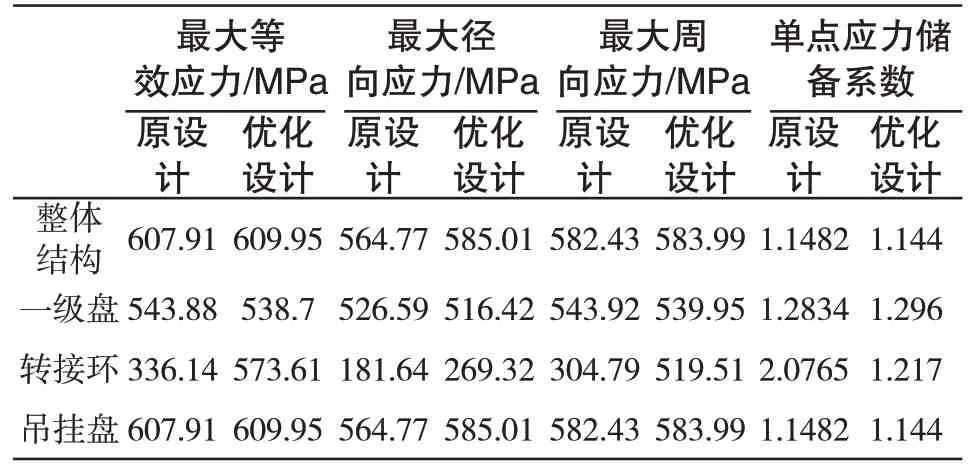
表6 原结构与改进螺栓连接结构等效应力、径向应力及周向应力计算结果Tab.6 Calculation results of equivalent stress,radial stress and circumferential stress of original structure and optimized structure with bolt connection
5 结论
1)通过对轮盘原设计结构与焊接变形后结构的强度计算分析,结果表明焊接造成的变形降低了轮盘的强度储备系数,并且每一个轮盘组件焊接变形位置和变形位移大小具有一定的偶然性,无法完全满足设计要求,给燃气轮机运行带来安全隐患。
2)原设计结构与焊接变形结构的最大等效应力出现于吊挂盘内径吊耳处,最大径向应力出现于吊挂盘前圆倒角处,而最大周向应力同样出现于一级盘吊耳处。因此,吊挂盘内径吊耳结构以及一级盘倒角等结构需要重点关注,并可进行适当的结构优化以降低应力水平。
3)焊接变形结构的最大等效应力和最大周向应力相对原设计结构有微小增加,但最大径向应力增大明显,单点应力储备系数降低。
4)优化设计结构传扭可靠性分析结果,即最大可传递扭矩大于最大工作扭矩,表明螺栓连接结构能够满足摩擦传扭要求;强度校核计算表明优化后的结构与原设计结构比较变化不大,满足设计需求。另外,转接环圆角和吊挂盘吊耳处相对危险,经进一步改进结构计算证明,可对转接环和吊挂盘进行结构优化以降低应力水平。

