风储联合电站实时自调度的高效深度确定性策略梯度算法

宋煜浩 魏 韡 黄少伟 吴启仁 梅生伟

风储联合电站实时自调度的高效深度确定性策略梯度算法

宋煜浩1魏 韡1黄少伟1吴启仁2梅生伟1

（1. 清华大学电机工程与应用电子系 北京 100084 2. 中国三峡新能源（集团）股份有限公司 北京 101100）

发展风电等可再生能源对于实现双碳目标具有重要意义，风储联合电站是未来风电接入电网的主要形式。该文研究发电侧商业化运行的风储联合电站的实时自调度问题，目标是使自身的期望收益最大化。由于场站级风电预测误差较大，独立发电商信息有限，难以准确预测电网电价，风储联合电站实时自调度面临多重不确定性，极具挑战。该文提出高效深度确定性策略梯度（DDPG）算法求取风储联合电站实时自调度策略，实现不依赖预测的场站级在线决策。首先通过Lyapunov优化构建基础策略，得到一个较好的但未必是局部最优的策略；然后，采用基础策略预生成样本，用于初始化经验库，提升搜索效率；接着，应用引入专家机制的DDPG算法，可以训练得到局部最优的自调度策略；最后，算例分析表明，相比于基础调度策略和经典DDPG，该文所提方法能有效提升风储联合电站的平均收益。

风储联合电站 实时自调度 Lyapunov优化 深度确定性策略梯度（DDPG）

0 引言

近年来，新能源发电发展迅速。以风电为例，截至2021年底，我国风电累计装机容量已经超过3亿kW，同比增长16.6%[1]，仅2022年一季度便新增风电790万kW[2]。风能作为一种绿色能源有望在未来的低碳电网中发挥主要作用。然而风能本身的波动性和随机性却给电力系统的运行带来了巨大的挑战，需要足够的备用资源。储能可以平滑风电出力，风储联合电站是未来风电接入电网的主要形式[3-5]。

本文考虑由独立发电商管理的风储联合电站参与实时市场，发电商的目标是最大化期望收益。由于场站级风电预测误差较大[6]，且独立发电商信息有限，难以准确预测电网电价[7]，风储联合电站实时自调度面临多重不确定性，极具挑战。目前关于风储联合电站调度优化的方法可大致分为以下几类。

1）基于模型预测控制（Model Predictive Control, MPC）或称滚动优化[8]。该方法利用一个预测模型求解当下的最优策略，如此随时间向前推进。文献[9]中提出了风储联合电站协调调度运行的框架。然而，MPC方法的性能依赖预测的精度。在最坏的情况下，与无预测的贪婪算法相比，MPC并不能带来更好的性能[10]。

2）基于两阶段鲁棒优化或者随机规划。随机规划假设不确定量的分布已知，对目标函数的期望值进行优化[11]。鲁棒优化考虑不确定集合中的最坏情况[12]。如采用随机规划方法研究风储联合电站参与电力市场问题[13]，采用鲁棒优化的方法研究风储联合电站在微网中的能量管理问题[14]。这一类方法的主要问题在于，第二阶段需要假设所有时段的不确定量都已获知后才能做出决策，无法用于在线调度。

3）以Lyapunov优化[15]为代表的在线优化方法，这一类方法既不需要预测也不需要历史数据。通过构造储能荷电状态的虚拟队列，将队列长度作为惩罚项加入目标函数，从而将时段耦合的优化问题分解为单时段决策。文献[16]将Lyapunov优化用于风储联合电站的实时调度，提升长期收益。此类方法的共性问题在于惩罚项引入目标函数可能会影响算法性能，导致得到的策略具有保守性。此外，完全忽略历史数据与预测信息也会影响策略的最优性。

4）基于以强化学习为代表的近似动态规划算法。相比于前两类方法，强化学习为数据驱动，其本身不依赖预测信息且便于实现在线决策。而相比于Lyapunov优化，强化学习可以充分利用历史数据的价值。强化学习在电力系统调度问题中已有较多应用[17-19]。特别地，对于风储联合电站的调度，目标包括最小化弃风[20]和最大化收益[21]等。

在强化学习算法中，深度确定性策略梯度（Deep Deterministic Policy Gradient, DDPG）算法[22]适用于状态和动作都为连续量的场景，和风储联合电站的调度问题兼容性较好。然而，在不依赖预测的前提下，鲜有研究将DDPG算法应用于风储联合电站的实时自调度中。如文献[23]将DDPG算法用于风储联合电站日前调度，文献[24]研究风光储联合系统在线调度，都使用了预测信息，性能依赖预测精度。此外，当调度时段较多时，各时段策略函数不同，离线训练效率降低；由于给储能充电没有即时收益，在训练时智能体容易短视而影响性能。这些也大大增加了DDPG算法应用于本文问题的难度。

Lyapunov优化利用了系统运行模型，可以有效规避不可行的调度动作和低收益动作，作为先验知识提升DDPG的探索效率；DDPG则可以充分利用历史数据的价值，通过训练，降低Lyapunov优化的保守性。鉴于二者具有互补性，本文提出高效DDPG算法。以Lyapunov优化作为基础策略，用于初始化DDPG的训练，求取风储联合电站实时自调度策略，实现不依赖风电出力和电价预测的场站级在线决策。最后对实际数据进行算例分析，通过和经典DDPG算法的对比，验证了所提策略的有效性。

1 风储联合电站自调度的数学模型

风储电站及其内部潮流如图1所示。电站通过一条输电线和主网相连，其传输容量是有限的。风能既可以直接通过传输线送到电网，也可以储存在配套储能中。储能从风机充电，向电网放电。为了提高收益，风储电站需要在电价低时储存风能，在电价高时卖出电能。然而在实时自调度的场景下，未来风电出力和电网电价是不确定的，传统优化模型只能作为离线策略提供最优值的基准，并不能提供在线策略。以下分别描述离线模型和在线模型。

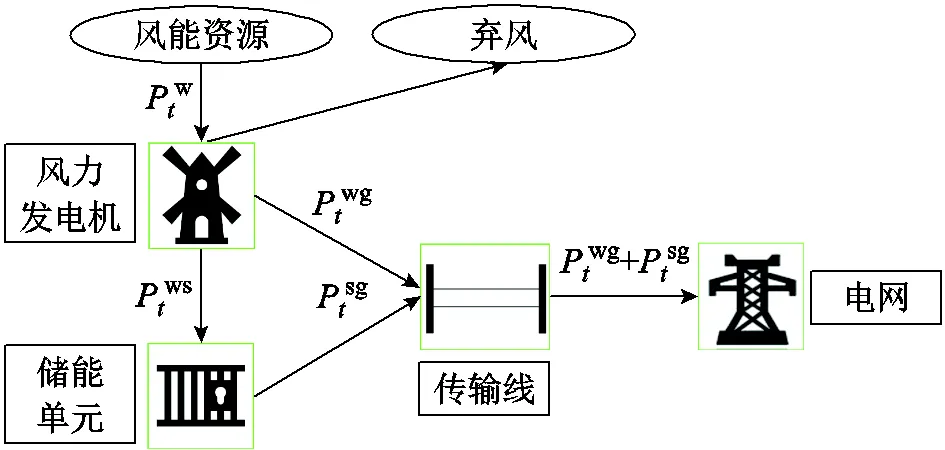
图1 风储电站及其内部潮流

1.1 离线模型

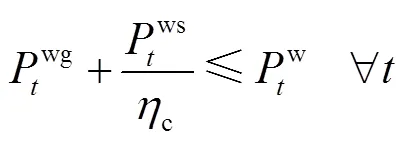
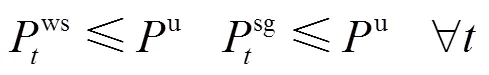
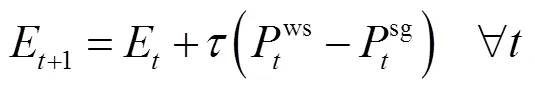
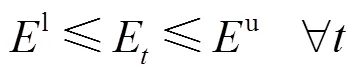
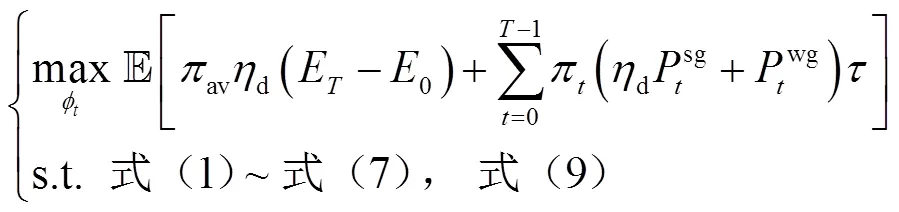
由于各阶段状态不存在不确定量，式（8）退化为式（10），形式上属于线性规划。

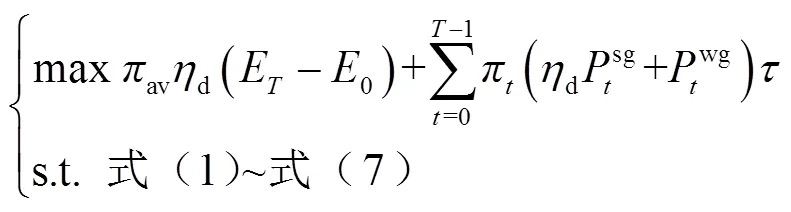
1.2 在线模型

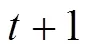
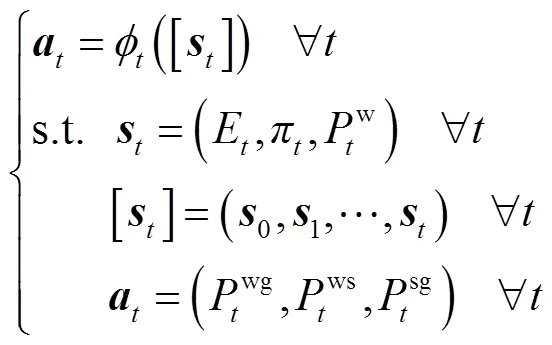
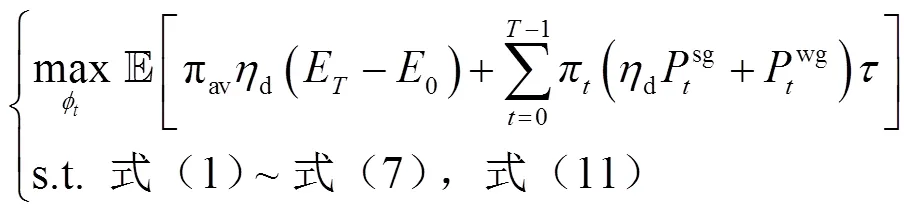
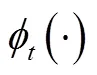
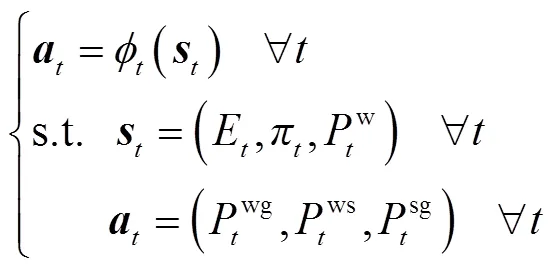
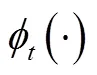
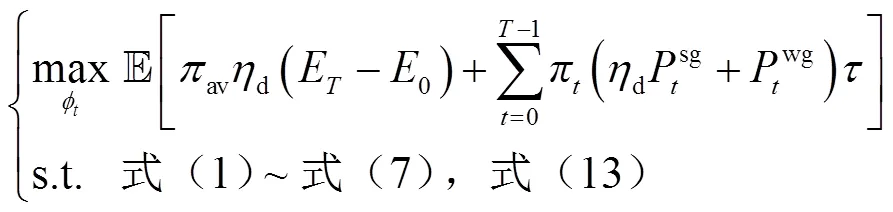
为了得到性能较优的策略，实现在线自调度模型（14）的求解，本文先基于Lyapunov优化理论得到一个基础调度策略，用该策略生成初始样本。随后提出高效DDPG算法，训练智能体改进基础调度策略。

2 基于Lyapunov优化的基础调度策略

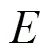
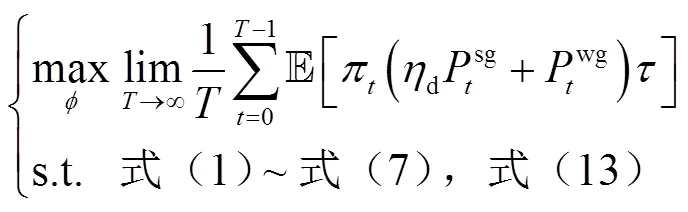
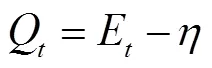
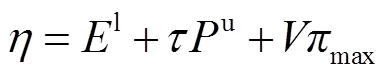
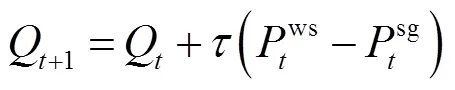
选择二次函数（19）为Lyapunov函数[15]。

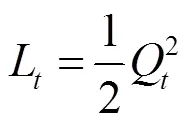
相邻两个时期的Lyapunov函数增量定义为漂移，即

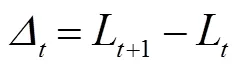
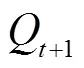
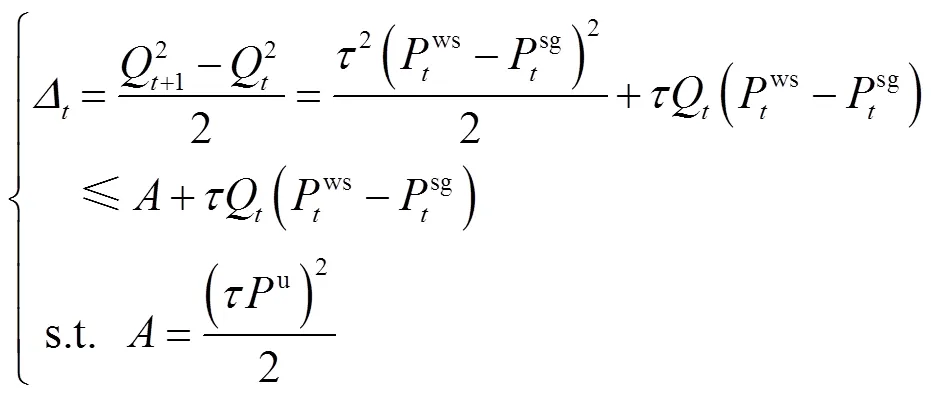
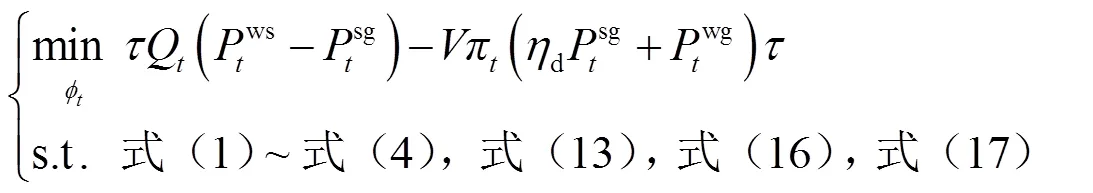
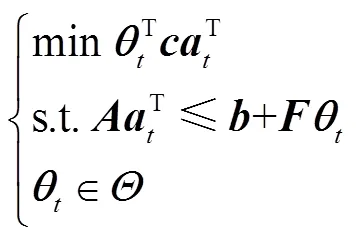
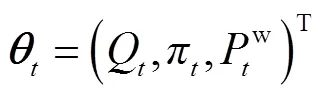
、和为常矩阵，为常向量，即

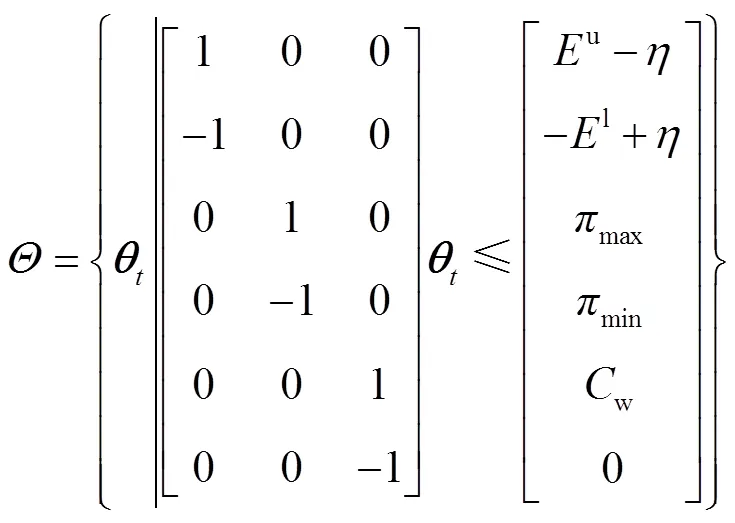
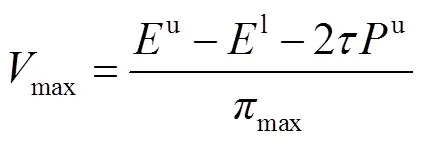
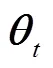
3 基于DDPG的改进调度策略

基于Lyapunov优化的基础调度策略求解速度快，然而，由于完全忽略了历史数据和预测信息，可导致应用效果偏保守或贪婪，在一定程度上损失了最优性。本节在基础策略的基础上，利用历史数据通过DDPG算法改善策略的表现。基础策略利用了系统模型，提升了智能体的探索效率，相比于经典DDPG性能更好。

3.1 自调度的MDP表述

式（14）可以看作一个马尔可夫决策过程（Markov Decision Process, MDP）[27]。

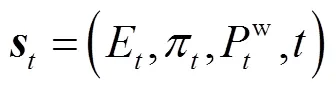
SOC的状态转移由式（5）描述。如果忽略实时电价和风机实时出力的长程相关性，可近似认为下一时期的状态不受过去时期状态和动作的影响，而受到当前时期状态和动作的影响，由此体现了MDP表述的合理性。

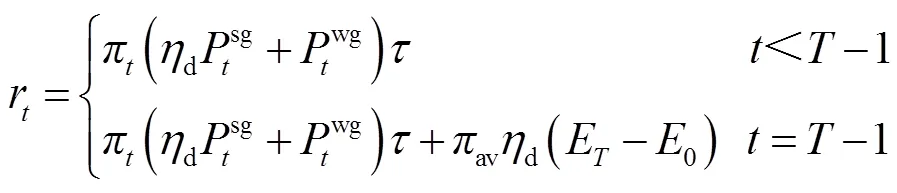
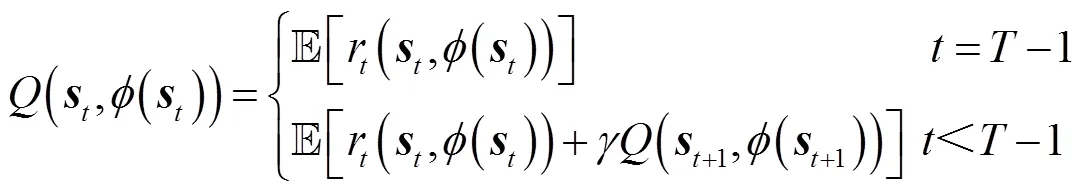
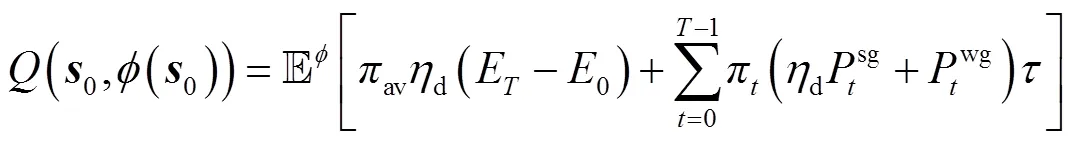
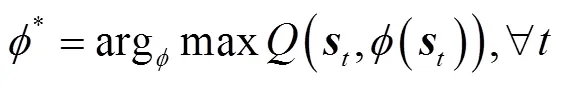
3.2 DDPG算法

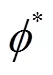
表1 DDPG神经网络

Tab.1 Neural networks of DDPG

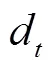
训练时，Actor评估网络的目标为最大化其输出动作的函数值，其损失函数为

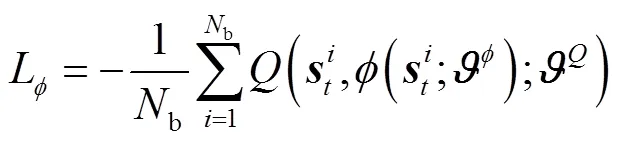
Critic评估网络的目标是最小化和目标网络之间的时间差分损失。

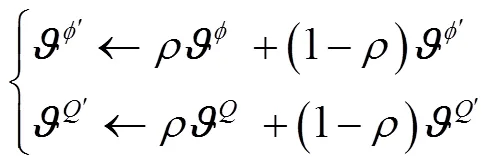
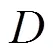
3.3 动作降维

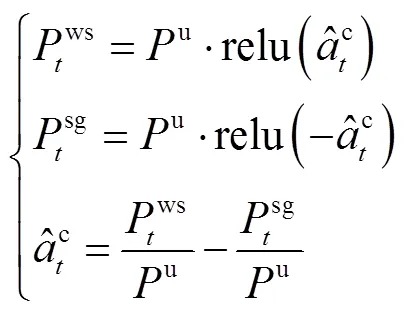
式中，relu()定义为当＞0时，relu()=；否则，relu()=0。

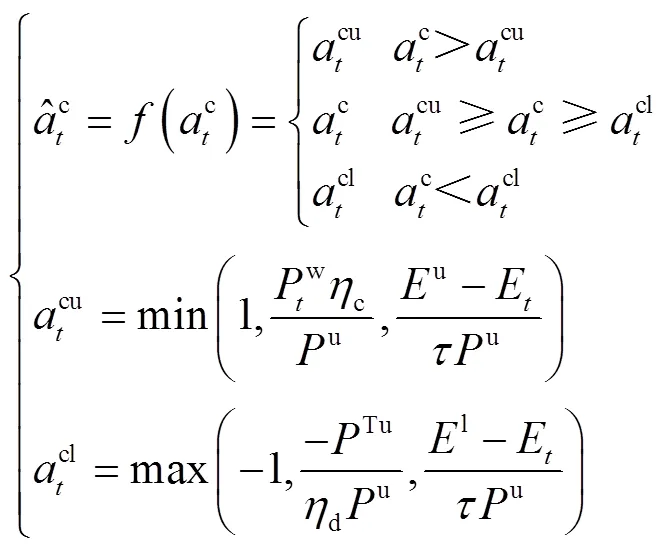
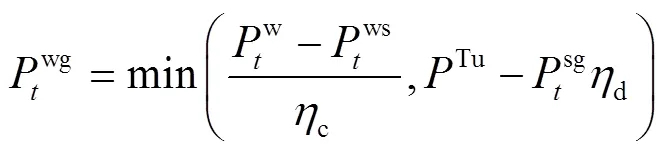
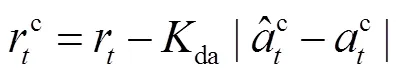
可以验证，采用式（38）替换3.1节中原有奖励式（28）得到新的MDP问题，其最优策略及最优值都是不变的，因此该问题和式（14）仍是等价的，但是训练难度降低了。

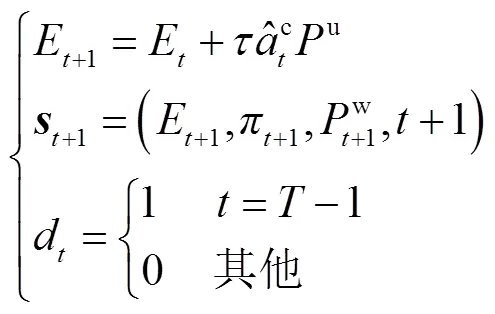
3.4 策略初始化与高效DDPG算法

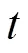
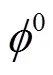
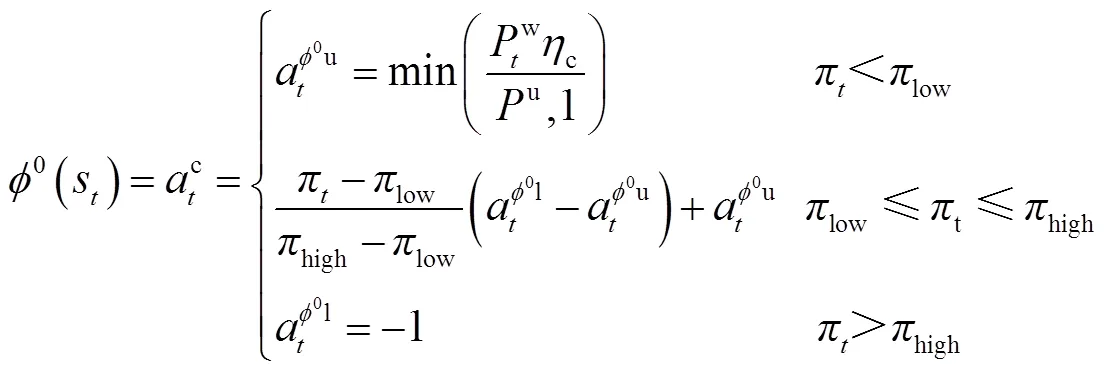
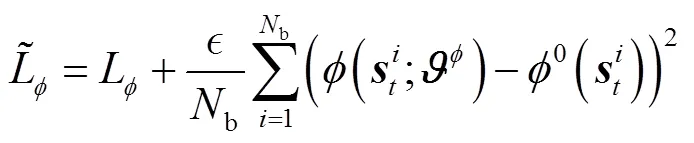
引入基于基础策略的样本初始化和专家机制后，求解自调度MDP模型的高效DDPG算法结构如图2所示。

图2 高效DDPG算法结构

表2 高效DDPG算法训练流程

Tab.2 Efficien DDPG algorithm training process

算法1是在基础调度策略样本的基础上进一步训练。相比于之前的基础策略，性能有进一步的提升。当训练完成后，Actor评估网络可以直接用于调度动作的生成，由此得到表3中的改进调度策略。由于神经网络的前馈在ms级时间即可完成，该策略是实时的，满足在线需求，并且不依赖于对未来不确定量的预测。但由于利用了历史数据，电价与风电出力的日变化模式包含在了最优动作价值函数式（29）中，因此具有一定前瞻性，可以获得比基础策略更好的性能。

表3 改进调度策略

Tab.3 Real-time self-dispatch improved strategy

4 算例分析

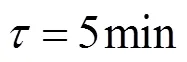
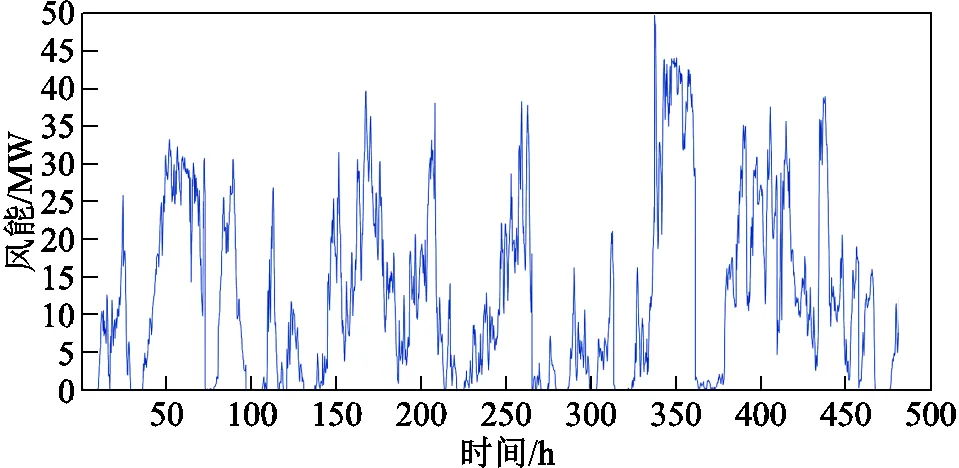
图3 风机实时出力（测试集）

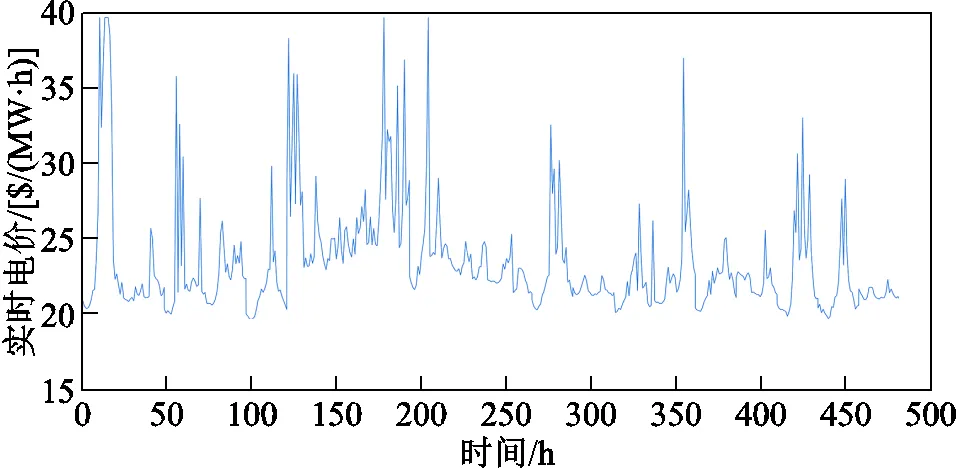
图4 实时电价（测试集）

表4 风储电站参数

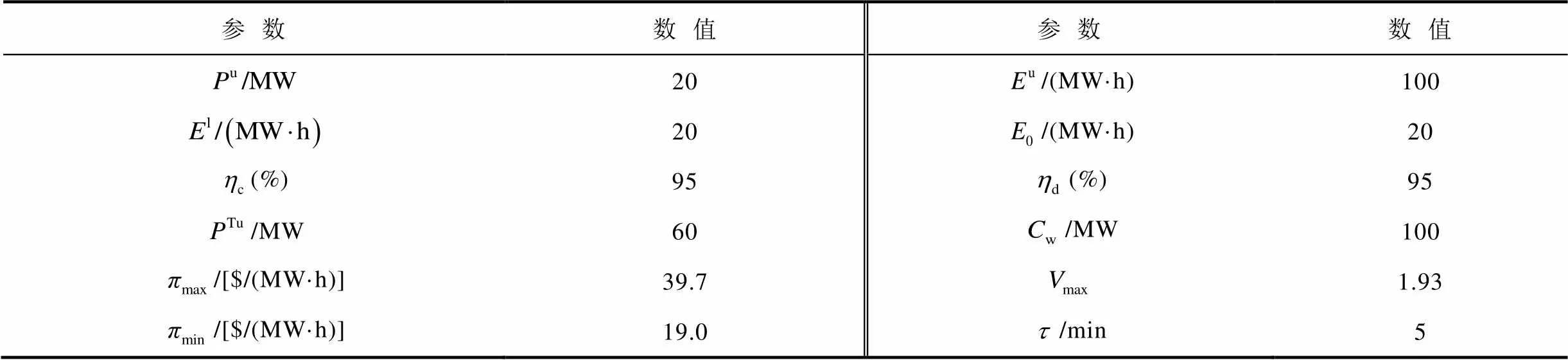
Tab.4 Wind - storage power plant parameters

表5 高效DDPG算法的超参数

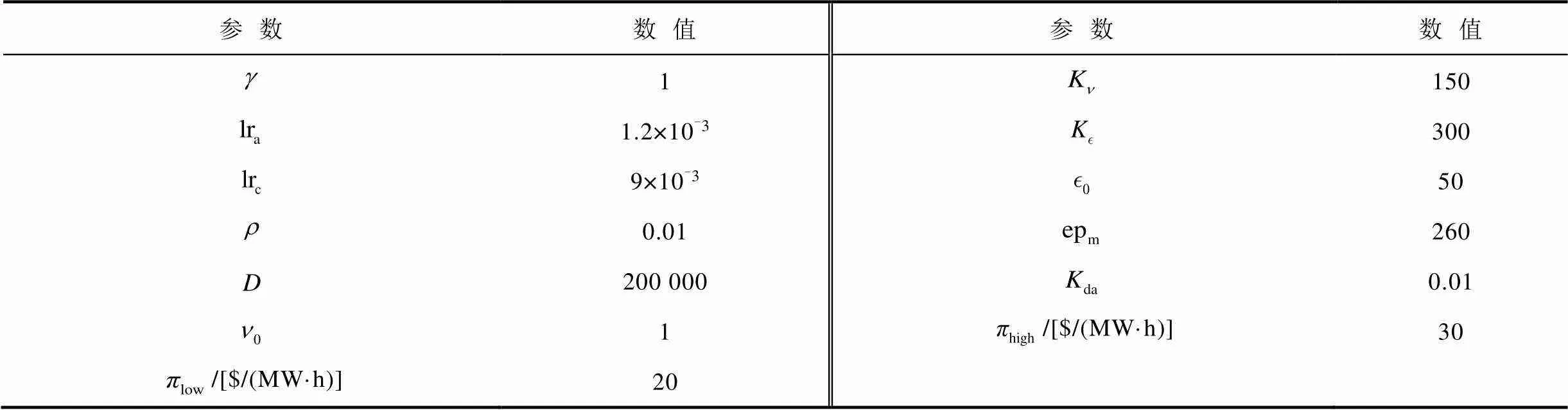
Tab.5 Hyperparameters of the improved DDPG algorithm

表6 神经网络的结构和优化器

Tab.6 Structure and optimizer of neural networks

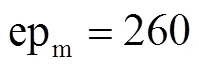
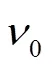
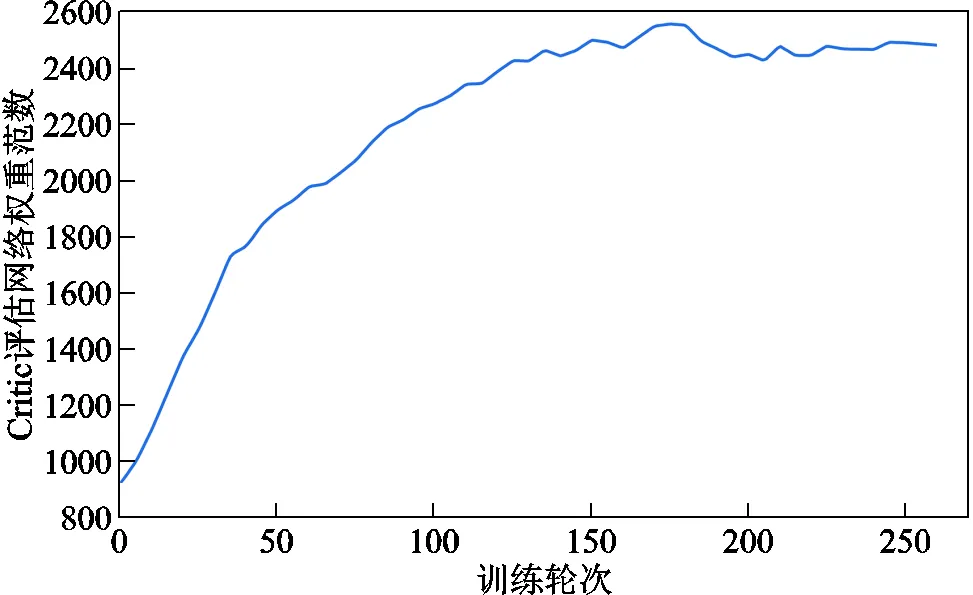
图5 神经网络权重—训练轮次曲线

在测试集上测试改进调度策略、经典DDPG算法训练的智能体及基础调度策略三种算法，结果见表7。在运行效果方面，三种策略不可行点数都为0，说明这些策略都运行在安全范围内，没有给出越界的调度动作；在SOC方面，改进策略的平均日最大SOC高于经典DDPG，但都小于12%，说明储能容量比较充足，而基础调度策略的平均日最大SOC高达43.68%，这是因为Lyapunov漂移惩罚项倾向于将SOC稳定在50%附近；在收益方面，改进调度策略的性能最好，经典DDPG算法的效果最差，前者比后者收益增加了2.60%，比基础调度策略增加了1.80%。由此可见，在基础调度策略基础上进行的DDPG训练提升了其性能，而基础策略的样本初始化及专家机制这一改进也明显提升了DDPG的训练效果。在运行过程中，改进调度策略给出的调度动作都是可行的且平均收益相对其他两种策略都有明显提升，证明了算法的有效性。

表7 平均性能比较（测试集）

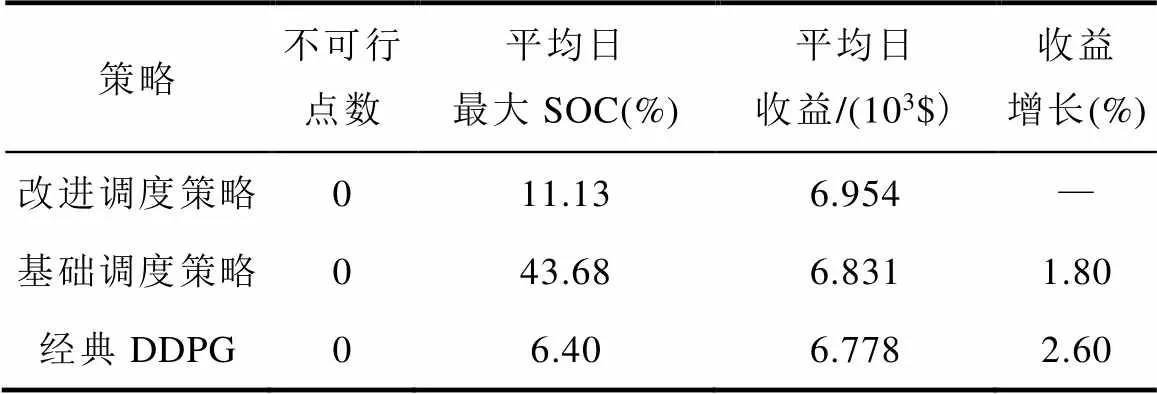
Tab.7 Average performance comparison (test set)

为了进一步对比策略的性能，选取测试集第19天，对比改进调度策略和基础调度策略的放电功率，如图6所示，其SOC曲线如图7所示。可以看到这一天的电价波动较大，凌晨时在22$/(MW·h)以下而下午则一度逼近30$/(MW·h)。基础策略的充电行为波动剧烈，放电行为出现在11:00电价上涨之后，然而随着SOC的下降，式（20）中的Lyapunov漂移惩罚项开始影响决策，在临近15:00出现了“高价充电”的情况；此外，在3:00附近由于长时间满充，SOC较高，类似地也出现了“低价不充”的现象。这些都影响了其最终的收益。而改进策略的充电行为比较平滑，如在0:00～5:00时SOC较低且电价有下降趋势，因此不断增加充电功率，5:00以后SOC达到较高水平且电价有上升趋势，因此充电功率迅速减小。由此，改进策略基本满足“低充高放”，且改进策略对电价变化的响应非常灵敏。

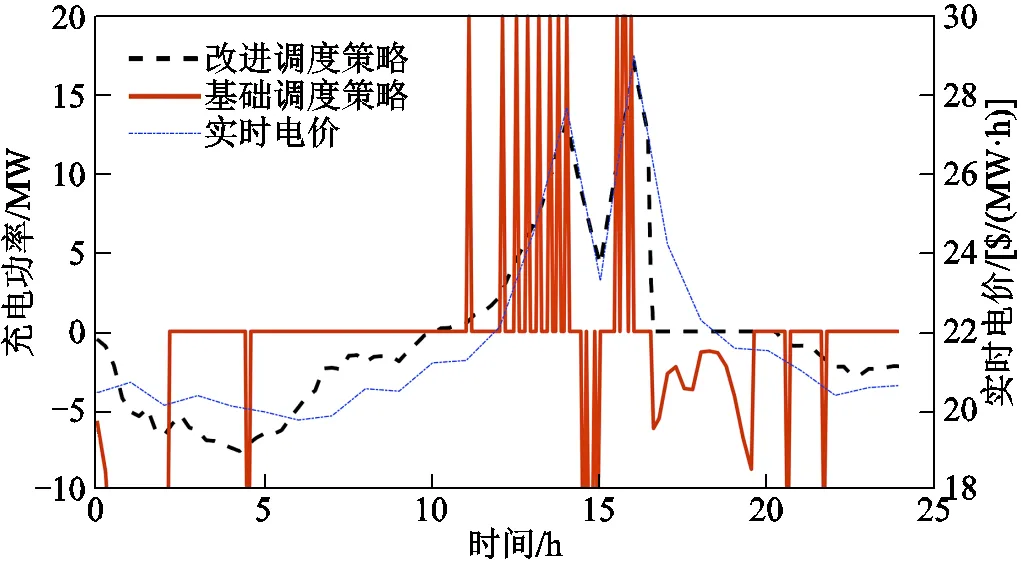
图6 放电功率对比（测试集第19天）

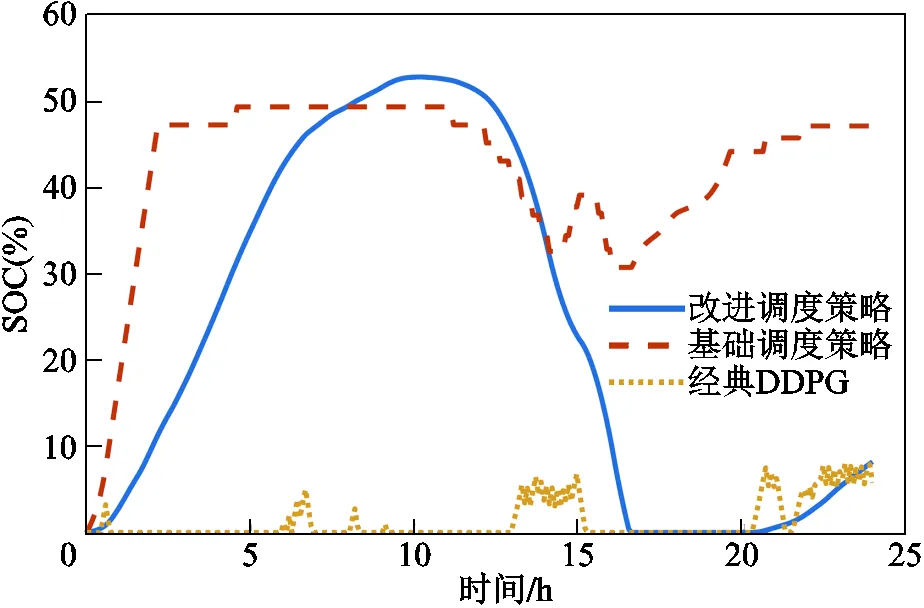
图7 SOC对比（测试集第19天）

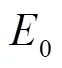
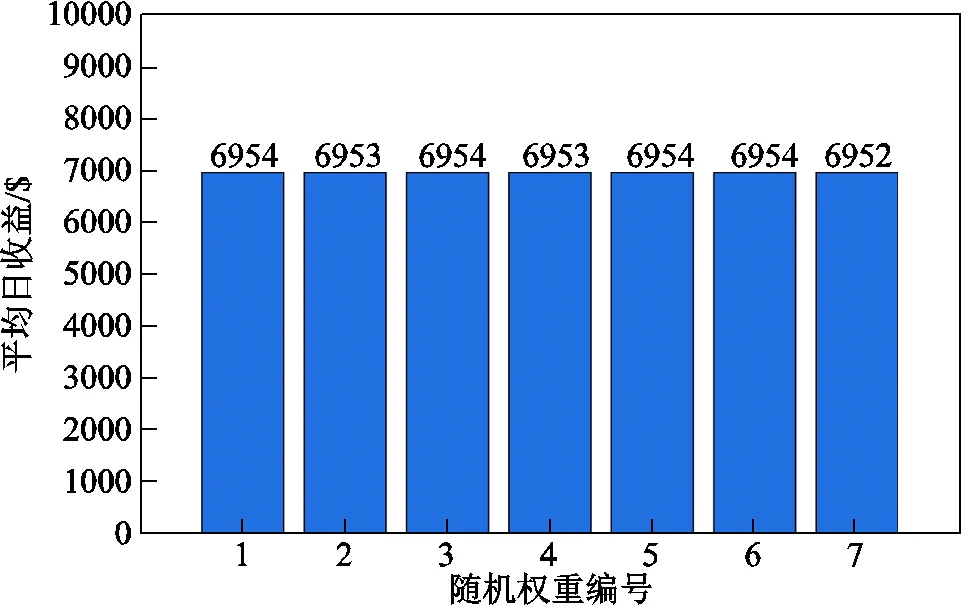
图8 随机权重对算法结果的影响

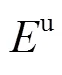
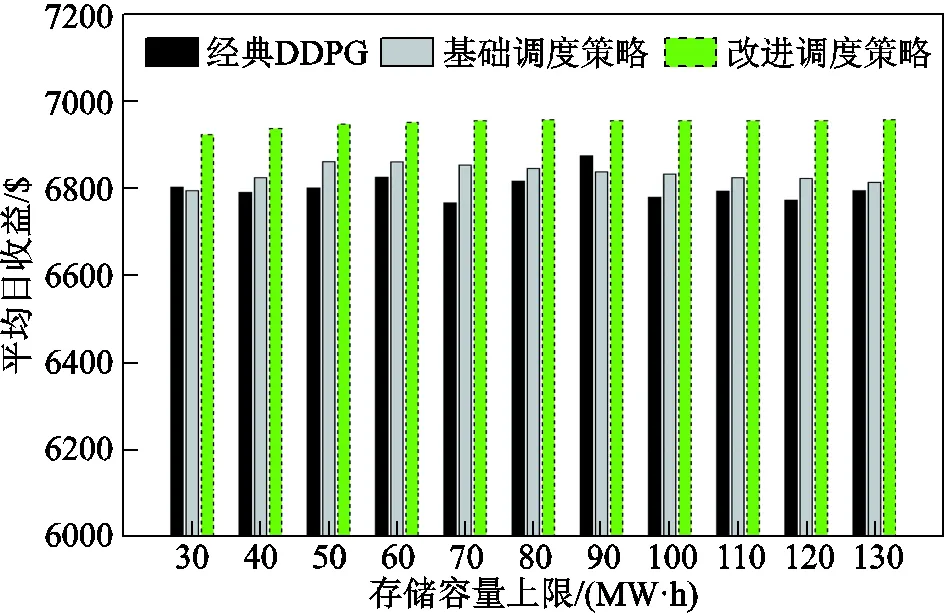
图9 容量变化对算法结果的影响

5 结论

本文针对传输线并网的风储联合电站的实时自调度问题，从并网上电经济收益最大化目标出发，利用基于Lyapunov优化的基础调度策略，由高效DDPG算法得到改进调度策略。通过和经典DDPG算法的对比，论证了该策略的有效性。结果表明：

1）改进调度策略在提升经济收益方面效果较佳。第4节的仿真算例表明，在风电和电价等预测信息未知的条件下，本文所提方法相比于基础调度策略和经典DDPG算法得到的调度策略，平均收益都有明显提升。

2）基础调度策略引入了额外的保守性，经典DDPG算法容易陷入不给储能充电的解。高效DDPG算法用基础调度策略进行初始化并引入专家机制，训练效率高。由此得到的改进调度策略更充分地利用了储能的存储容量，对电价变化的响应灵敏。

3）高效DDPG算法收敛性较好。离线训练的智能体在线应用，满足了自调度的实时性需求。

[1] 国家能源局. 2021年全国电力工业统计数据[EB/OL]. [2022-01-26]. http://www.nea.gov.cn/2022-01/26/c_1310441589.htm.

[2] 国家能源局. 截至3月底全国发电装机容量约24亿千瓦,3月份可再生能源发电量较快增长.[EB/OL]. [2022-04-22]. http://www.nea.gov.cn/2022-04/22/c_ 1310569074.htm.

[3] 姜书鹏, 乔颖, 徐飞, 等. 风储联合发电系统容量优化配置模型及敏感性分析[J]. 电力系统自动化, 2013, 37(20): 16-21.

Jiang Shupeng, Qiao Ying, Xu Fei, et al. Capacity optimization and sensitivity analysis of cogeneration system of wind power and energy storage[J]. Automation of Electric Power Systems, 2013, 37(20): 16-21.

[4] 陆秋瑜, 罗澍忻, 胡伟, 等. 集群风储联合系统广域协调控制及利益分配策略[J]. 电力系统自动化, 2019, 43(20): 183-191.

Lu Qiuyu, Luo Shuxin, Hu Wei, et al. Wide-area coordinated control and benefit assignment strategy of clustering wind-energy storage integrated system[J]. Automation of Electric Power Systems, 2019, 43(20): 183-191.

[5] 孙辉, 刘鑫, 贲驰, 等. 含风储一体化电站的电力系统多目标风险调度模型[J]. 电力系统自动化, 2018, 42(5): 94-101.

Sun Hui, Liu Xin, Ben Chi, et al. Multi-objective risk scheduling model of power system containing power station with integrated wind power and energy storage[J]. Automation of Electric Power Systems, 2018, 42(5): 94-101.

[6] 王佳丽. 探路风电预报[J]. 能源, 2014(3): 74-76.

Wang Jiali. Pathfinder wind power forecast[J]. Energy, 2014(3): 74-76.

[7] 姚子麟, 张亮, 邹斌, 等. 含高比例风电的电力市场电价预测[J]. 电力系统自动化, 2020, 44(12): 49-55.

Yao Zilin, Zhang Liang, Zou Bin, et al. Electricity price prediction for electricity market with high proportion of wind power[J]. Automation of Electric Power Systems, 2020, 44(12): 49-55.

[8] García C E, Prett D M, Morari M. Model predictive control: theory and practice—a survey[J]. Automatica, 1989, 25(3): 335-348.

[9] Xie Le, Gu Yingzhong, Eskandari A, et al. Fast MPC-based coordination of wind power and battery energy storage systems[J]. Journal of Energy Engineering, 2012, 138(2): 43-53.

[10] Lin Minghong, Liu Zhenhua, Wierman A, et al. Online algorithms for geographical load balancing[C]//2012 International Green Computing Conference (IGCC), San Jose, 2012: 1-10.

[11] Wu Hongyu, Shahidehpour M, Li Zuyi, et al. Chance-constrained day-ahead scheduling in stochastic power system operation[J]. IEEE Transactions on Power Systems, 2014, 29(4): 1583-1591.

[12] Ben-Tal A, Nemirovski A. Robust solutions of uncertain linear programs[J]. Operations Research Letters, 1999, 25(1): 1-13.

[13] Garcia-Gonzalez J, de la Muela R M R, Santos L M, et al. Stochastic joint optimization of wind generation and pumped-storage units in an electricity market[J]. IEEE Transactions on Power Systems, 2008, 23(2): 460-468.

[14] Lara J D, Olivares D E, Cañizares C A. Robust energy management of isolated microgrids[J]. IEEE Systems Journal, 2019, 13(1): 680-691.

[15] Neely M J. Stochastic network optimization with application to communication and queueing systems[M]. Berlin: Springer, 2010.

[16] Guo Zhongjie, Wei Wei, Chen Laijun, et al. Real-time self-dispatch of a remote wind-storage integrated power plant without predictions: explicit policy and performance guarantee[J]. IEEE Open Access Journal of Power and Energy, 2021, 8: 484-496.

[17] 赵冬梅, 陶然, 马泰屹, 等. 基于多智能体深度确定策略梯度算法的有功-无功协调调度模型[J]. 电工技术学报, 2021, 36(9): 1914-1925.

Zhao Dongmei, Tao Ran, Ma Taiyi, et al. Active and reactive power coordinated dispatching based on multi-agent deep deterministic policy gradient algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1914-1925.

[18] 李涛, 胡维昊, 李坚, 等. 基于深度强化学习算法的光伏-抽蓄互补系统智能调度[J]. 电工技术学报, 2020, 35(13): 2757-2768.

Li Tao, Hu Weihao, Li Jian, et al. Intelligent economic dispatch for PV-PHS integrated system: a deep reinforcement learning-based approach[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2757-2768.

[19] 刁浩然, 杨明, 陈芳, 等. 基于强化学习理论的地区电网无功电压优化控制方法[J]. 电工技术学报, 2015, 30(12): 408-414.

Diao Haoran, Yang Ming, Chen Fang, et al. Reactive power and voltage optimization control approach of the regional power grid based on reinforcement learning theory[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 408-414.

[20] 梁煜东, 陈峦, 张国洲, 等. 基于深度强化学习的多能互补发电系统负荷频率控制策略[J]. 电工技术学报, 2022, 37(7): 1768-1779.

Liang Yudong, Chen Luan, Zhang Guozhou, et al. Load frequency control strategy of hybrid power generation system: a deep reinforcement learning—based approach[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1768-1779.

[21] 于一潇, 杨佳峻, 杨明, 等. 基于深度强化学习的风电场储能系统预测决策一体化调度[J]. 电力系统自动化, 2021, 45(1): 132-140.

Yu Yixiao, Yang Jiajun, Yang Ming, et al. Prediction and decision integrated scheduling of energy storage system in wind farm based on deep reinforcement learning[J]. Automation of Electric Power Systems, 2021, 45(1): 132-140.

[22] Lillicrap T P, Hunt J J, Pritzel A, et al. Continuous control with deep reinforcement learning[EB/OL]. 2019: arXiv: 1509.02971. https://arxiv.org/abs/1509. 02971

[23] 蔡新雷, 崔艳林, 董锴, 等. 基于改进K-means和MADDPG算法的风储联合系统日前优化调度方法[J]. 储能科学与技术, 2021, 10(6): 2200-2208.

Cai Xinlei, Cui Yanlin, Dong Kai, et al. Day-ahead optimal scheduling approach of wind-storage joint system based on improved K-means and MADDPG algorithm[J]. Energy Storage Science and Technology, 2021, 10(6): 2200-2208.

[24] 张淑兴, 马驰, 杨志学, 等. 基于深度确定性策略梯度算法的风光储系统联合调度策略[J/OL]. 中国电力, 2022: 1-9. [2022-07-03]. http:// kns.cnki.net/ kcms/ detail/11.3265.TM.20211115.1426.002.html.

Zhang Shuxing, Ma Chi, Yang Zhixue, et al. Joint dispatch of wind-photovoltaic-storage hybrid system based on deep deterministic policy gradient algorithm [J/OL]. Electric Power, 2022: 1-9. [2022-07-03]. http://kns.cnki.net/kcms/detail/11.3265.TM. 20211115. 1426.002.html.

[25] Shen Ziqi, Wei Wei, Wu Danman, et al. Modeling arbitrage of an energy storage unit without binary variables[J]. CSEE Journal of Power and Energy Systems, 2021, 7(1): 156-161.

[26] 束金龙, 闻人凯. 线性规划理论与模型应用[M]. 北京: 科学出版社, 2003.

[27] Sigaud O, Buffet O. Markov decision processes in artificial intelligence[M]. New York: John Wiley & Sons, 2013.

Efficient Deep Deterministic Policy Gradient Algorithm for Real-Time Self-Dispatch of Wind-Storage Power Plant

Song Yuhao1Wei Wei1Huang Shaowei1Wu Qiren2Mei Shengwei1

（1. Department of Electrical Engineering Tsinghua University Beijing 100084 China 2. China Three Gorges Renewables (Group) Co. Ltd Beijing 101100 China）

The development of wind power and other renewable energy is of great significance to achieve the dual carbon goal, and the wind-storage power plant is the main form of wind power connected to the power grid in the future. This paper studies the real-time self-dispatch problem of the wind-storage power plant commercialized on the generating side, with the goal of maximizing its expected income. Due to the large prediction error of the field-level wind power and the difficulty in accurately predicting the electricity price of the grid due to the limited information of independent power producers, the real-time self-dispatch of the wind-storage power plant is faced with multiple uncertainties, which is extremely challenging. In this paper, an efficient DDPG algorithm was proposed to solve the real-time self-dispatch strategy of the wind-storage power plant, and realize the field-level online decision-making independent of prediction. Firstly, Lyapunov optimization was used to construct the basic strategy to obtain a good but not necessarily local optimal strategy. Then, samples were pre-generated by the basic strategy to initialize the experience base and improve the search efficiency. Further, DDPG algorithm with expert mechanism was applied to train the locally optimal self-scheduling strategy. Case study shows that compared with the basic dispatch strategy and the classical DDPG, the proposed method can effectively improve the average revenue of the wind-storage power plant.

Wind-storage power plant, real-time self-dispatch, Lyapunov optimization, deep deterministic policy gradient(DDPG)

10.19595/j.cnki.1000-6753.tces.220979

TM614

中国长江三峡集团有限公司科研项目资助（202003128）。

2022-05-30

2022-07-18

宋煜浩 男，1998年生，博士研究生，研究方向为储能技术的应用。E-mail：3160871816@qq.com

黄少伟 男，1985年生，博士，副研究员，硕士生导师，研究方向为人工智能在电力系统中的应用。E-mail：huangsw@mail.tsinghua.edu.cn（通信作者）

（编辑 赫蕾）