具有时变延迟和扰动的非线性系统自适应学习控制*

孙云平，李金绪，郑平安

(云南师范大学 信息学院，云南 昆明 650500)

延迟和扰动常存在于实际的控制系统中，导致系统性能的降低[1-10]，同时存在时变延迟和扰动的系统由于时变扰动的导数不等于零，对其进行理论研究相对困难，一般会利用自适应界化技术对时变扰动进行处理，但是得到的结果不太理想[11].本文研究了一种具有时不变扰动及不确定周期时变扰动和延迟的非线性系统的重复学习控制问题，利用文献[12-13]提出的自适应周期控制方法，对时不变和时变扰动分别设计了参数学习律，并利用Lyapunov-Krasovskii函数消除时变延迟影响，提出基于李亚普诺夫理论的混合重复学习控制方案.

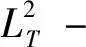
1 问题描述

考虑下列非线性系统

(1)

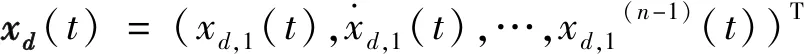
假设1 函数f(·,·)满足李普希茨条件，即

|f(x,x(t-τ))-f(xd,xd(t-τ))|≤l(‖x-xd‖+‖x(t-τ)-xd(t-τ)‖),

(2)

其中l是未知李普希茨常数.

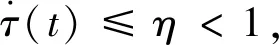
假设3g(x,θ(t),ϖ)=θ(t)ξ(x,t)ϖ,其中θ(t)=(θ1(t),θ2(t),…,θn(t))∈R1×n是周期为T的未知连续时变参数向量，ϖ=(ϖ1,…,ϖn)T∈Rn×1是未知的时不变参数向量，ϖ的每个分量ϖi的符号是已知的(i=1,2,…,n)，不妨设ϖi>0,ξ(x,t)=diag{ξ1(x,t),ξ2(x,t),…,ξn(x,t)}是已知矩阵函数.

假设4θ(t+T)=θ(t)属于某个紧集，且θi(t+T)=θi(t)，存在未知正数θM<∞，使得‖θ(t)‖≤θM.

以下推导过程中，除了特别说明，将省略t.

2 控制律与参数学习律的设计

系统(1)的跟踪误差的动态方程为

(3)

其中，

选取适当的κ,使多项式sn+κ1sn-1+…+κn-1s+κn为Hurwitz多项式，从而可以找到给定常数ω>0,存在正定矩阵P>0,I为单位矩阵，满足

(4)

为了消除延迟，设计Lyapunov-Krasovskii函数

(5)

其中γ>0为设计增益，对(5)式求导，得

(6)

由(4)式，得到

(7)

由假设1知|Λ|≤|l(‖e‖+‖e(t-τ)‖)|,因此

|eTPCb-1Λ|≤|eTPCb-1|l(‖e‖+‖e(t-τ)‖)|.

(8)

利用Young′s不等式，得

eTPCb-1Λ≤γ-1(eTPCb-1l)2+0.5γeTe+0.5γeT(t-τ)e(t-τ).

(9)

将(9)式代入(7)式，得

(10)

由假设2，可以得到

(11)

由(11)式，设计控制律

(12)

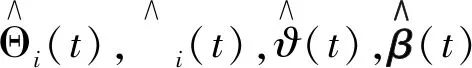
设计时变参数周期学习律

(13)

(14)

时不变参数学习律

(15)

(16)

其中r1,i>0,r2,i>0,q1>0分别是设计的常增益;Γ是正定对称矩阵.

设q0(t)=tT-1q1,r0,i(t)=tT-1r1,i,t∈[0,T)，那么r0,i(t),q0(t)在[0,T)上是严格单调增加的连续函数，从而有r0,i(0)=0,r0,i(T)=r1,i;q0(0)=0,q0(T)=q1.

将(12)式代入(11)式，得

(17)

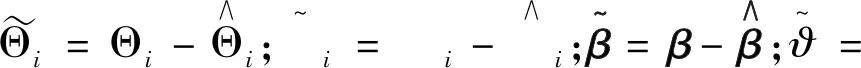
(18)

3 收敛性分析

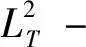
证明定义Lyapunov函数

(19)

对于 ∀t≥T,E(t)在[t-T,t)的差分

(20)

分别计算(20)式等号右边每一项.由(18)式，可知

(21)

由Θi(t)=Θi(t-T)和(13)式，得到

(22)

由ϑ(t)=ϑ(t-T)和(14)式，得

(23)

由(15)式，得

(24)

由(16)式，得

(25)

由(21)-(24)式，(20)式变为

(26)

因α>0，r1,i>0,q1>0，ϖi>0，从而

(27)

对t∈[jT,(j+1)T]，多次利用(27)式，记t0=t-jT，则

(28)

因为t0∈[0,T),对(28)式求极限，得

(29)

由(13)-(16)式，学习律在[0,T)上变为

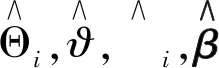
下面，只需考虑t∈[T1,T)上，E(t)的有界性.

由r0,i(t),q0(t)的取值，有

r1,i≥r0,i(t)≥r0,i(T1)>0;q1≥q0(t)≥q0(T1)>0;2r1,i>r0,i(t)>0;2q1>q0(t)>0.

对(19)式求导，得

(30)

由(22)-(25)式，可得

结合(30)式，得

从而得到

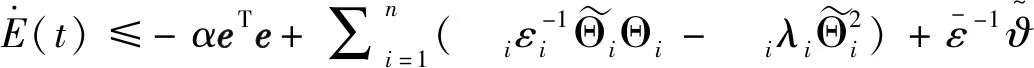
(31)

将上式代(31)式，得

(32)

4 数值仿真

为了验证算法的有效性，考虑二阶非线性系统

(33)

其中,

选取κ=[1,2]T,q1=1,r1,j=1,r2,j=1,q0(t)=tT-1q1,r0,i(t)=tT-1r1,i(i=1,2),取ω=4,有P=[6,2;2,2].通过编程仿真，图1说明控制u(t)一定有界，图2和图3分别表明跟踪误差最大绝对值渐近收敛于0，证明所提算法是可行有效的.

图1 控制u(t) 图2 跟踪误差e1 图3 跟踪误差e2Fig.1 Controller u(t) Fig.2 Tracking error e1 Fig.3 Tracking error e2

5 结语

根据Lyapunov稳定性理论，将学习控制和自适应控制相结合，设计自适应学习控制方案，处理了被控系统中的未知延迟和干扰等不确定性因素，从而达到控制系统稳定性的目的，提高了系统的性能和指标.数值仿真表明了所提算法是有效和可行的.