基于改进动态域遗传算法的神经元控制器参数优化*

鲜 阳，谭 飞

(四川轻化工大学自动化与信息工程学院，宜宾 644000)

0 引言

遗传算法理论基本思想是基于进化论和遗传学说[1-2]。由于遗传算法不依赖被求解的目标函数本身，具有较强的全局搜索能力、适用范围广、鲁棒性强，得到了较多的工程应用[3-4]。HWANG、王剑楠等[5-7]认为遗传算法和神经网络、模糊逻辑一起构成了“软计算”的三大基石，但算法还是存在编码、选择交叉、计算效率、精度等方面的一些问题需要解决，吸引了大量的科技工作者对它进行研究改进。杜嘉伟等[8]提出一种基于矩阵二进制编码的改进遗传算法，通过对初始种群的编码以及降维保证了合理的初始适应度，使算法有优良的全局和局部搜索能力，但未在高维数据下验证可行性。周凯等[9]设计了一种基于二进制和实数编码的混合编码多种群遗传算法，能有效提高计算效率和求解精度，但定义的优化模型的目标函数较少，显得算法适应性不足。而本文以十进制编码遗传算法为基础，从提高算法收敛全局性、收敛精度两个方面进行相关设计，通过大量代表性测试函数对比分析，将其用于挖掘机的神经元控制系统参数优化，取得的结果说明算法具有很好的工程适应性。

1 归一化十进制编码与解码

讨论遗传算法的编码方法的文献有很多[10-11]，多数文献是以二进制和浮点编码进行讨论，而讨论十进制整数编码的文献有少量，且主要是变异问题存在缺陷，收敛效果不佳。

本算法设优化问题如式(1)所示。

z=maxf(x)x=(x1,x2,…,xm)∈S⊆Rm

(1)

式中，xi∈[ai,bi]，i=1,2,…,m；ai,bi∈R分别为xi的下界和上界；m为目标函数变量维数。

该十进制整数编码是把目标函数的每一维变量的定义域规范到1，域间的点属于[0,1]间，然后放大(10d-1)倍，得到变量基因位的编码值，如式(2)所示。

(2)

编码是变量xi离散过程，其误差与10-d成正比，d越大，误差越小。解码时通过式(3)可得变量值xi。

(3)

编码取各变量的基因长度相同，不需处理符号位和定义域的宽度。

2 动态域遗传算法设计

2.1 种群初始化

Zp×1=f(Vp×m),Vp×m→Cp×md

(4)

2.2 交叉与选择

算法交叉，父代采用精英策略，其中一个父代固定为备选库中的最优个体，另一个通过二选一择优机制从库中随机抽取。采用两点交叉法，如式(5)所示。

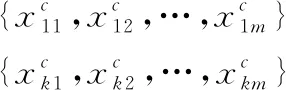
(5)

交叉完成规定子代的产生，译码求解目标函数值，然后子代与父代备选库一起按适应值从大到小排序，并去除相似个体，择优选择排在前的n1条个体组成下一代备选库的一部分。

2.3 算法的变异策略

2.3.1 基因补全变异

在二进制遗传算法中，变异是通过0和1的互变实现，因为它的状态只有两个，很易满足每个等位基因都存在基因0和1的全集，而高进制算法互补运算很难实现等位基因为0～n-1的全集。本算法采用基因补进方法实现，方法是，检查备选库编码阵C，按列查找缺失的等位基因。比如，查询哪些列缺失基因0，采用最优个体编码ce，修改相应等位基因为0，得到补进基因值0的个体，如式(6)所示。

(6)

把十进制的0～9的基因值补完，最多可得到10条染色体，并译码加入到备选库中。该方法可大概率提高优秀个体与缺失基因的组合，提高算法全局优化能力。

2.3.2 重生变异

重生变异就是以最优个体xe为中心随机从当前定义域中生成多个点，方法如式(7)所示，译码加入到父代备选库中。重生策略可增加备选库基因模式的多样性。这种策略也相当于是一种变异，可称为重生变异。

(7)

这两种变异个体的补充，构成了每列各种十进制基因都存在的完整父代备选库。

2.4 动态域调整

提高算法寻优精度的办法可以采用实时缩小算法搜索范围来解决，搜索范围小，精度就越高，但全局性兼顾是个问题。解决这个矛盾本算法采用动态域方法，结合到前面精英交叉策略，把这算法称为动态域精英遗传算法(dynamic domain and elite genetic algorithm，DDEGA)。

按式(8)检查最优个体的改善速度是否满足要求，成立则进行动态域调整。

ze-ze0<α·|ze0|或ze-ze0<α

(8)

式中，ze和ze0分别为当前和前一代的最优适应值；α∈(0,1)，通常α取0.05或再小一点。

动态域搜索调整如图1所示，有两个阶段。第一阶段式(8)不满足时，采用式(10)调整域边界，这是动态界1法，此法使各维变量边界同步整体缩小。

B1=min(|b0-a0|)

(9)

a1=a0+B1/β，b1=b0-B1/β，β>2

(10)

式中，a0和b0分别为上代的下界和上界；a1和b1为变量x调整后的下界和上界；β为一个常数，本算法取10，若取更大，搜索域缩小很快，不利于全局寻优。式(8)成立，域进一步缩小。

图1 算法搜索动态域示意图

在域1里边界变化后，首先复制最优个体，备选库的其他个体用重生策略随机产生。若最优个体的任何一维值离域边界的距离小于容错变量tol，则进入动态界2调整，以每维变量为中心，缩小搜索域。

B2=max(|b1-a1|)

(11)

a2=xe-B2/β，b2=xe+B2/β，β>2

(12)

式中，a2和b2分别为调整后变量下界和上界。调整后界要限制到原始定义域内。

动态界2方法，以式(8)为准则，使边界逐次缩小，当边界宽度小于tol或最优个体离边界距离小于tol时，恢复边界到最初定义域，复制精英个体，其他备选库个体重新初始化产生，然后继续遗传搜索。

2.5 算法步骤

算法的停止条件可设置多个。当达到最大代数、或者达到寻优精度等条件都可停止寻优，显示参数和结果，完成计算。

按照以上所述，DDEGA算法的流程图如图2所示。

图2 DDEGA算法流程图

2.6 算法全局收敛性分析

研究算法时，采用设置d=3，去除动态域法，只应用前述的基于精英交叉策略的遗传算法(elite genetic algorithm，EGA)，或者不用精英交叉，两个父体都用联赛选择的遗传算法(league matches genetic algorithm，LMGA)，比较它们的收敛特性。

由于算法随时从搜索域随机补充新个体，且每次边界恢复时从全域重生新个体种群，使种群丰富多样，从而减小了算法陷入局部最优的概率。可以证明每一次重生策略和搜索域恢复时都从全局随机取点，取到全局最优解的概率可以达到1 ，所以DDEGA具有全局最优收敛能力。

3 算法测试

为便于比较，测试条件一致，测试函数选择文献[12]所列部分Benchmark函数如表1所示。为了说明精英策略的有效性和快速性，把EGA算法与LMGA算法进行测试比较；同时把动态域算法DDEGA与文献[12]的自适应直接变异浮点编码遗传算法ADMRCGA(adaptive directed mutation for real-coded genetic algorithm)进行比较。文献[12]列了6种算法，ADMRCGA是其最好的一种。

算法设种群为60，编码精度为14位，交叉操作后通过排序择优选择得45个个体，基因补全可最多得到10个个体，重生操作添加补足总数，它们一起构成下一代交叉备选库种群。选函数维数为30，最大评价30万次，独立运行30次统计结果如表2所示。

本文算法采用MATLAB2020a在RTX2060、8 G内存、Win10系统下编程实现。函数优化停止条件：①达到最大代数；②100代适应值不变；③与全局最优值绝对误差小于阀值1E-8。只要满足任一条件就终止迭代进化。采用30代独立运行进行统计比较，如表2、表3所示。

表1 BENCHMARK测试函数

表2 函数30次独立运行的均值与方差

表3 函数的平均耗时及评价次数

从表3可以看出DDEGA计算结果在函数f1～f4、f6～f8比算法ADMRCGA高很多，并且从表3可以看出DDEGA算法搜索计算时间很短，说明DDEGA算法收敛很快。但DDEGA算法要进一步提高精度，得适当增加编码长度，与浮点编码比较，在要求非常高精度时受到一定限制。结合表2和表3可以看出，在不用动态域方法时，很难达到1E-8的要求精度。在相同评价计算次数下，基于精英策略的算法精度要优一些。由于篇幅限制，列了两个函数的收敛过程如图3和图4所示，可以看出，基于精英策略的算法EGA在初始阶段的收敛速度比联赛算法LMGA要快，但从表3看，后继的精确搜寻能力比较，LMGA的能力比EGA相对稍微强点，平均来看还是EGA比LMGA好点。几种算法中，DDEGA是精英策略与动态域方法结合，有了快速与精确的搜索能力，使遗传算法的速度得到了质的飞越。实验还发现DDEGA在函数f7、f8上的收敛效果比文献[13]的基于精英学习的动态差分算法还好，说明遗传算法的性能并不逊于现代差分进化算法，有它独有的魅力。

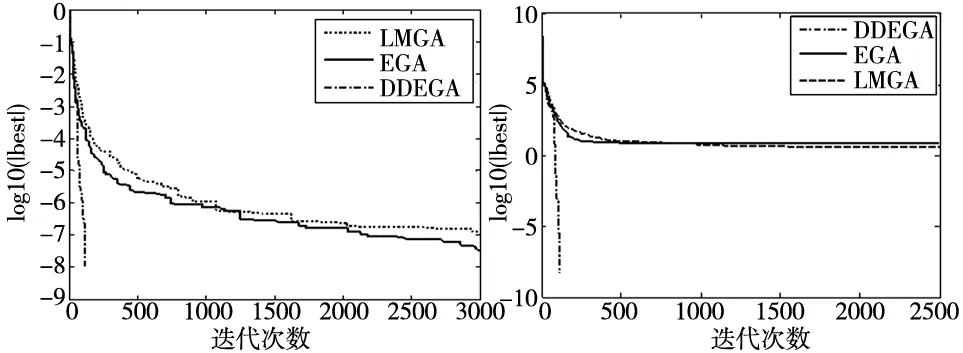
图3 f3函数收敛曲线 图4 f7函数收敛曲线

4 算法的应用

神经网络技术发展并应用到控制中，解决了很多常规PID控制无法解决的问题。增量PID控制算法和神经网络技术的结合，得到了神经元PID控制算法[14-16]。一些神经元PID控制算法采用BP方法实现自适应控制，但效果不理想。虽然理论上证明，系统自学习调整控制参数，可以达到稳定收敛，但仿真发现，还是存在长时间学习后失稳的情况，但是在确定控制权重等参数后，系统的鲁棒性和控制性能比常规PID好很多。所以神经元控制的应用最好是离线学习后用于在线参数整定。

神经元PID控制系统的结构如图5所示。采用动态域精英遗传算法优化神经元PID控制系统的权值。

图5 神经元PID控制系统

神经元控制单元算法如式(13)、式(14)所示，这种结构便于系统投运，控制的总增益K可根据实际情况及时在线调整，权值设置好后可不再调整。

x1(k)=Δe(k)
x2(k)=r(k)-y(k)=e(k)
x3(k)=e(k)-2e(k-1)+e(k-2)

(13)

u(k)=u(k-1)+Ktanh[ω1x1(k)+ω2x2(k)+ω3x3(k)]

(14)

式中，ωi为加权系数。

被控对象取某挖掘机伺服系统特性：

(15)

设采样时间0.1 s对Gp(s)进行离散，对控制器的3个权值寻优。目标函数取ITAE和ISE如式(16)所示，优化到最小。

(16)

式中，tm为仿真终止时间，取30 s。

图6 挖掘机伺服控制系统的阶跃响应曲线

该目标函数是一个复杂的多峰函数，寻优发现在K不定的情况下优化得到的权值解不唯一。本次优化把K固定等于1.5(连续系统的临界增益)，ω1和ω3取值范围[0,1]；虽然对象由积分特性，但仿真发现ω2不能为0，否则对定值控制的稳态偏差将失去修正能力，所以寻优取值范围确定为[0.001,1]。本文算法对系统进行10次寻优，每次评价5000次得到的ITAE结果，ω1=0.268 7，ω2=0.001，ω3=0.164 7；ISE的优化结果，ω1=0.451 5，ω2=0.005 4，ω3=0.364 9。这些结果同ZN法整定的PID控制结果做比较如图6所示。可见算法取得了优良控制质量。可以验证在这权值下把K放大3倍或缩小到1/3，系统不会失去稳定，神经元PID控制系统具有很好的鲁棒稳定性。

5 结论

本文提出的基于精英策略动态域整数编码遗传算法，采用归一化十进制整数编码求解连续定义域函数最大值问题，它编码方便，不用考虑符号位和定义域的大小，同样情况下比二进制编码求解效率高。实验表明它算法具有全局寻优和求精的能力，并且快速稳定收敛于理论目标，具有良好的收敛特性，搜索性能优越。本算法缺陷在于采用整数编码，有离散量化误差，进一步精度的提高将加大编码译码的复杂性，但精英学习的快速收敛能力、重生策略的全局最优保证能力、动态域的求精能力值得其他算法设计的学习。算法用于优化神经元PID控制系统，取得了成功，表明能很好解决工程优化实际问题。