基于高斯层次感知的知识图谱链接预测
胡雪若白,黄 洁,王建涛,李一鸣
(战略支援部队信息工程大学 数据与目标工程学院,河南 郑州 450000)
为了提高信息搜索效率,提升用户使用体验,谷歌公司于2012年创建了知识图谱。知识图谱的发展经历了语义网络、知识表示、本体论、Semantic Web、自然语言处理等技术发展阶段,并继承了来自Web、人工智能和自然语言处理等多领域的技术优势[1]。知识图谱利用图模型来描述知识,能够直观地建模物体之间的关联关系。
知识图谱中包含节点以及边,其中节点表示实体,实体表示了现实世界中存在的知识;边代表知识之间的关联关系[2],其既可以是实体的属性,也可以是实体之间的关系。现有的知识图谱中存在着海量知识,知识图谱能够提供海量的事实知识,建立从客观世界的知识到结构化语义描述的映射,因此知识图谱能够为辅助智能问答、自然语言理解、推荐计算、可解释性人工智能等多个领域的应用与实现提供数据和技术支持[3]。但是,现有的知识图谱存在明显的知识缺失,需要对知识图谱进行知识推理以补全知识图谱,为后续知识图谱的应用提供丰富知识支撑,因此知识图谱推理对知识图谱的发展演变十分重要。
基于表示学习的推理通过知识图谱嵌入(Knowledge Graph Embedding,KGE)方法,将知识图谱中包括实体和关系的元素映射到一个连续的向量空间中,学习实体和关系在向量空间中的表示[4],使之能够通过向量空间表示之间的计算来自动实现知识图谱的推理。该领域常见的算法包括Trans系列模型算法[5]、基于三阶张量表示学习算法RESCAL[6]、基于流形的表示模型算法MainfoldE[7]、深度神经网络算法NTN[8]、ConvE[9]等。
在知识图谱分布式表示算法中,最常用的是Trans系列模型,其中最经典的是TransE[5]模型。在TransE模型中,知识图谱中的每个实体和关系都通过模型表示成一个低维向量,若该三元组成立,则头实体向量h与关系向量r的和与尾实体向量t相近。尽管TransE模型能够有效学习实体的分布式表示,但其对于实体间多对多的关系表示仍然存在着一些缺陷。文献[10]中提出了TransH模型,该模型假设每个关系r都有一个对应的关系超平面,将实体映射到关系指定的超平面,然后在该超平面上,将关系的分布式表示看作映射后实体之间的空间距离。该方法中,映射向量增加了同一实体在不同关系上的表示,一定程度上弥补了TransE模型不能有效处理实体间多映射关系的缺陷。文献[11]中提出的TransR模型为每个关系r都定义了一个语义空间,然后将实体映射到该语义空间中进行表示。文献[12]的映射考虑了实体和关系之间的交互,该研究在TransR的基础上,提出了更细粒度的TransD模型。文献[13]中提出了KG2E模型,该模型通过建模实体和关系的不确定性,在多维高斯空间中学习实体和关系的概率分布,通过衡量实体的转移分布与关系分布之间的能量距离KL散度,来精确地获取实体和关系的语义信息。本文基于实体与关系的能量距离和空间距离,设计了基于高斯层次感知的知识图谱链接预测模型,并将其命名为GHAKE(Gaussian Hierarchy-Aware Knowledge Graph Embeddings)。
1 改进的知识图谱链接预测
1.1 模型框架
在高斯层次感知链接预测模型中,分别将实体输入高斯嵌入模块和词向量嵌入模块,以获取实体和关系的高斯分布信息和表示向量。在高斯嵌入模块中,在获取实体和关系的高斯分布信息后,以实体概率分布和关系概率分布两个分布之间的相似性来衡量两个实体之间是否存在链接。在词向量嵌入模块中,将学习到的词向量嵌入到极坐标系中,以实体向量之间的空间距离来衡量实体之间是否存在链接。通过 D-S 证据理论将基于能量距离的得分与基于空间距离的得分进行融合,以联合得分来衡量实体之间的关系。高斯层次感知链接预测模型的结构如图1所示。
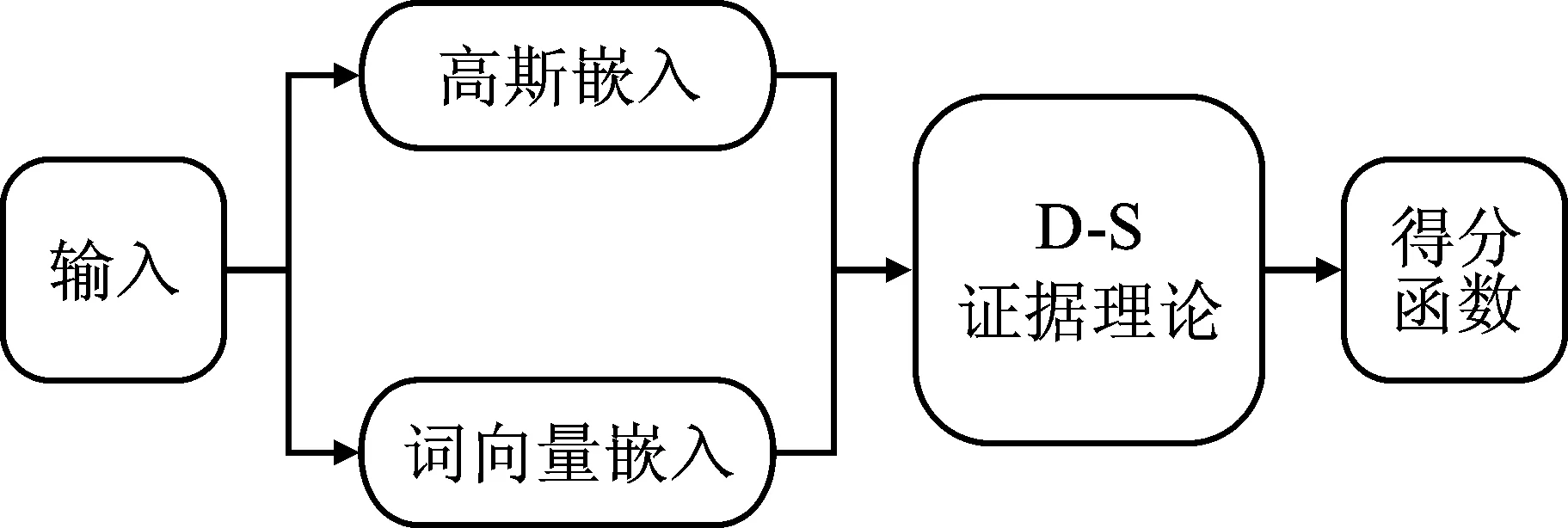
图1 高斯层次感知链接预测模型框架
1.2 基于高斯嵌入的实体关系表示
为了对实体的不确定性进行建模,本文使用变分自编码器(Variational Auto-Encoder,VAE)从节点属性中学习节点的概率分布函数,然后通过节点的概率分布函数表示来对实体嵌入的不确定性进行建模。均值向量表示节点在嵌入空间中的位置,协方差矩阵表示节点嵌入的不确定性。
(1)
使用H-T表示实体的分布变换,它对应于概率分布Pe~N(μh-μt,∑h+∑t),即头实体与尾实体之间的概率差。因此,结合关系的概率分布Pr~N(μr,∑r),最重要的步骤是测量Pe和Pr之间的相似性[13]。
Wasserstein距离是一种可用于测量两个概率分布的相似性的算法。根据实体分布和关系分布之间的Wasserstein距离定义的能量距离函数[14]为
ε(h,r,t)=ε(Pe,Pr)=W2(Pe,Pr)
=W2(N(μe,∑e),N(μr,∑r))
(2)
式中,tr(∑)代表协方差矩阵的迹。
本文引入正则化系数ε和Sinkhorn迭代方法来简化Wasserstein距离的计算过程。本文引入一个耦合矩阵P和一个距离矩阵C,其中耦合矩阵表示将点从Pe移到Pr所需的概率质量,而距离矩阵表示从点Pe移到Pr的成本。采用两个分布本身之间的耦合矩阵来衡量Pe和Pr之间的相似性。在高斯嵌入中,均值和协方差分别表示实体的位置和不确定性,因此可以获得耦合矩阵P和距离矩阵C,如式(3)和式(4)所示
P:{∑e-∑r}
(3)
C:{μe-μr}
(4)
得出总成本如式(5)所示。
(5)
但是,并非所有矩阵都是有效的耦合矩阵,因此需要引入约束条件:对于耦合矩阵,必须以概率质量Pr将其所有列添加到向量中。在进行Wasserstein距离计算时可以将两个向量分别表示为a和b,因此最优成本可以表示为
(6)
由此可将寻找两个分布之间距离的问题转换为求解最佳耦合矩阵的问题。定义耦合矩阵的熵为
(7)
由于具有较低熵的矩阵将更加稀疏,具有高熵的矩阵将更平滑,因此引入正则化系数ε以获得更平滑的耦合矩阵
(8)
引入熵正则化可以将求解最优耦合矩阵的问题转化为凸优化问题,并可以使用Sinkhorn迭代方法进行解决,即P=diag(u)Kdiag(v),在迭代过程中交替更新
(9)
(10)
其中,K是由C计算的核矩阵。
简化后的Wasserstein距离被描述为
ε(h,r,t)=
ε(Pe,Pr)=W2(Pe,Pr)=
W2(N(μe,∑e),N(μr,∑r))=

(11)

1.3 基于词嵌入的实体关系表示
通常情况下,实体之间的关联关系并不是简单的线性关系,而是自然地存在着多对多的关系,这些抽象的关系都可以用“树”结构来表示,例如公司企业中的职级关系,可以抽象地表示成一个“树”,如图2所示。
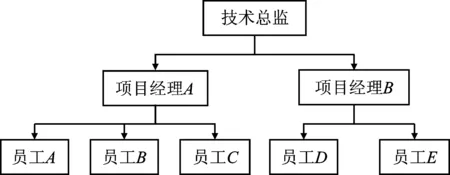
图2 企业职级关系
在本文中,将处在不同语义层级中的实体抽象表示为树结构,树中叶子节点的深度代表实体的语义层级。为了对知识图谱中实体语义层次进行建模,本文确立了知识图谱实体中的层次级别:(1)实体分布在同一个语义层级上,例如“项目经理A”和“项目经理B”以及“员工A”和“员工C”;(2)实体分布在不同的语义层级上,例如“技术总监”和“项目经理B”以及“项目经理A”和“员工A”。
为了对实体语义层级进行建模,GHAKE将实体的词向量嵌入极坐标系中:首先将由GLOVE[15]学习获得的词向量转换为包含模向量部分和相位向量部分的复向量;然后将词的复向量嵌入到极坐标系中,此时不同层级的实体将会展现在不同的层级上,因此可以实现对两个不同类别中的实体进行建模。实体语义层次感知模型的示例如图3所示。
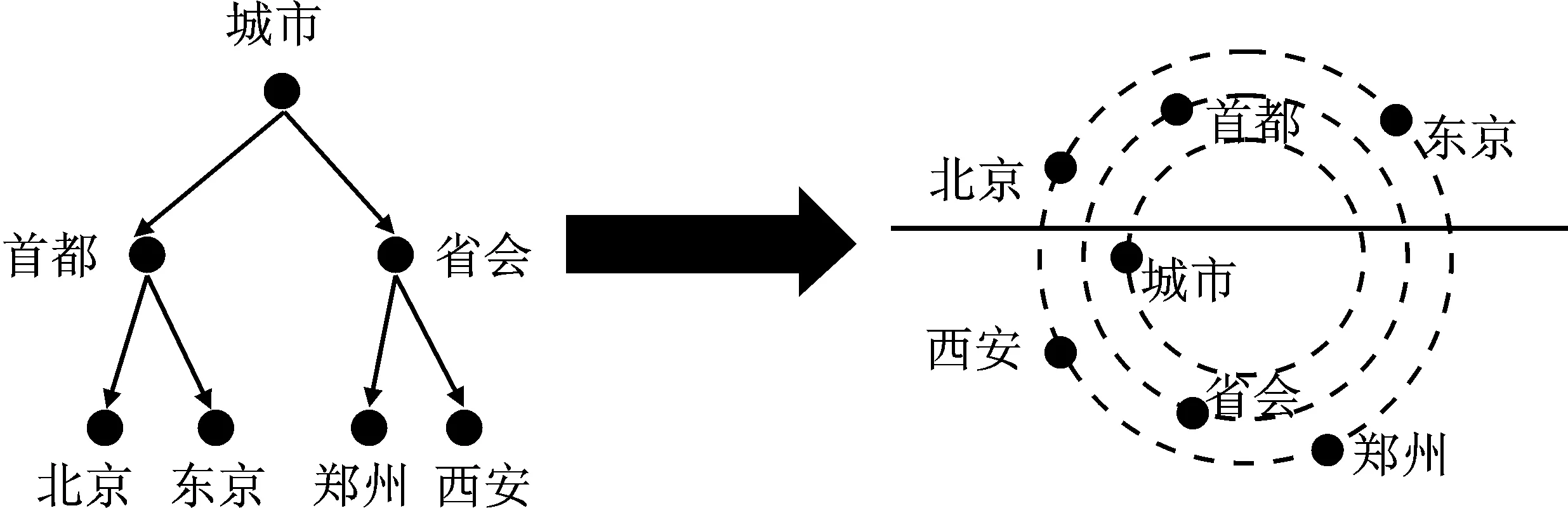
图3 层次感知模型的简单说明
为了区分实体嵌入的模向量部分与相位向量,本文分别使用em(e表示头实体h或尾实体t)和rm表示模数部分中的实体嵌入和关系嵌入;使用ep(e表示头实体h或尾实体t)和rp表示相位部分中的实体嵌入和关系嵌入。
模向量部分对处在不同语义层级的实体建模,并且树结构中不同层级的叶子节点,其在树中的深度便不相同。因此,使用实体嵌入的模向量可以对不同语义层级中的实体进行建模,其中模向量的数值反映了实体在语义结构中的深度。将每个头实体hm和每个尾实体tm的模向量嵌入视为实体表达的模量[16],并将每个关系rm视为两个实体模量之间的翻译转换
hm∘rm=tm,其中hm,tm∈d,rm∈d
(12)
相应的距离函数如式(13)所示。
dr,m(hm,tm)=‖hm∘rm-tm‖1/2
(13)
相位部分对语义层次结构相同级别上的实体建模,由于同一个同心圆上的实体的模向量相同但相位不同,因此可以使用实体的相位向量来区分处于同一语义层级上的不同实体,也就是将每个头实体hp和每个尾实体tp的相位嵌入视为实体表达的相位,并将每个关系rp的相位嵌入视为两个实体相位之间的相变
(hp∘rp)mod2π=tp,hp,tp,rp∈[0,2π)k
(14)
相应的距离函数为
dr,p(hp,tp)=‖sin((hp+rp-tp)/2)‖1
(15)
其中,sin(·)表示正弦函数。由于相位具有周期性特征,因此本文使用正弦函数来测量相位之间相变时,需要对相位进行2π取模。
GHAKE将模量部分和相位部分组合在一起,将实体映射到极坐标系中,其中映射向量的径向坐标和角坐标分别对应于实体分布式表示的模量部分和相位部分。因此,GHAKE对应的距离函数为
dr(h,t)=dr,m(hm,tm)+λdr,p(hp,tp)
(16)
式中,λ∈R为模型学习参数。相应的得分函数为式(17)。
fr(h,t)=-dr,m(h,t)-λdr,p(h,t)=-
‖hm∘rm-tm‖1/2-
λ‖sin((hp+rp-tp)/2)‖1
(17)
1.4 两种得分的融合
在高斯层次感知模型中,同时考虑基于能量的距离函数ε(h,r,t),即Wasserstein距离和空间距离函数fr(h,t),并以D-S证据理论融合两种得分函数[17]。
根据基于能量距离的得分函数得到其基本概率赋值函数
(18)

同理,根据基于空间距离的得分函数可以得到其基本概率赋值函数
(19)

融合两个基本概率赋值函数mε(h,r,t)和mfr(h,t),可以得到融合后的基本概率赋值函数
(20)
通过判定融合后实体链接的置信度可以判断两个实体之间是否存在链接。
2 实验验证
2.1 数据来源
本文在3个常用的数据集:WN18RR、FB15k-237和YAGO3-10上对本文提出模型进行评估。
在实验验证过程中,对于测试数据集中的每个三元组(h,r,t),算法样本生成时,将头实体h或尾部实体t替换为每个候选实体来创建1组候选三元组。

表1 WN18RR、FB15k-237和YAGO3-10的数据集信息
2.2 实验结果与分析
所提模型GHAKE与现有的最新链接预测方法以及经典的链接预测算法的性能的比较如表2所示,对比算法包括TransE、KG2E以及层次感知模型(Hierarchy-Aware Knowledge Graph Embeddings,HAKE)。本文选择均值倒数排名(Mean Reciprocal Rank, MRR)和N处的点击数(H@N)作为评估指标,本文分别取N=1,3,10, MRR或H@N越高表示性能越好。

表2 对WN18RR、FB15k-237和Y AGO3-10数据集的评估结果
表2展示了本文算法GHAKE与其他算法在链接预测准确性上的性能情况,最后一列为本文所提算法的结果。每个数据集中,链接预测性能表现最优的数据均为加粗形式。从表2中可以看出,本文模型GHAKE在所有数据集上的大部分性能表现较优,证明了GHAKE具有良好的链接预测功能。下文将针对每个数据集进行说明,从而充分体现本文所提算法的优势。WN18RR数据集中包含11个关系,这些关系可以分为对称关系(例如_derivationally_related_from链接同一级别的实体)和一些非对称关系(例如_member_meronynm链接不同级别的实体)。由于GHAKE将实体的不确定性添加到实体嵌入中,因此与HAKE相比,GHAKE在MRR指标和H@N指标上的表现略优,MRR指标提高了0.087,H@1提高了0.08,H@3提高了0.055,H@10提高了0.047。该结果证明本文的GHAKE可以有效地对实体的语义层次进行建模。YAGO3-10数据集由37个关系组成,其中包含对称和不对称关系。在YAGO3-10数据集中,一个三元组(, hasGender, female)具有1 000多个真实的对应头部实体。本文提出的模型GHAKE同时考虑了实体的不确定性和实体的语义层次,因此在链路预测任务中GHAKE的性能比HAKE略优,在MRR指标上提高了0.021,H@1提高了0.049,H@3提高了0.052,H@10提高了0.107。与WN18RR和YAGO3-10相比,FN15k-237数据集包含更复杂的关系和更少的实体,这无法清楚地描述实体的语义层次,给实体的语义层次带来了巨大挑战。但是,与现有模型相比,本文提出的模型在链接预测任务中仍然表现良好。
从表2中也可以看出,本文所提模型GHAKE在3个数据集上的链接预测的准确性优于HAKE与KG2E模型,这是由于KG2E模型在考虑实体与关系的不确定性分布时忽略了实体之间的语义层级关系,而HAKE模型在考虑实体的语义层级关系时忽略了实体与关系的不确定性。本文所提模型GHAKE同时考虑了实体与关系的不确定性以及实体之间的语义层级,因此在进行词嵌入时能更精确地对实体进行表征,提升实体链接预测的性能。
3 结束语
各类知识图谱链接预测算法虽然能够在不同程度上实现有效的链接预测,但较少有模型考虑实体间关系的不确定性。为了同时对知识图中实体的语义层次和不确定性进行建模,本文提出了一种高斯层次感知知识图嵌入模型GHAKE。该模型学习实体与关系的高斯分布表示与词向量表示,并将实体映射到极坐标系中建模实体之间的语义层级,通过D-S证据理论融合实体之间的能量距离与空间距离,进而提升了链接预测的性能。实验表明,GHAKE模型不仅能够对实体的不确定性进行建模,同时能够对语义层次结构中不同级别和相同级别的实体进行建模,提高了链接预测的精确度。对比实验表明,GHAKE模型在基准数据集上的链接预测性能优于现有的几种最新方法。

