组合加点准则的代理辅助多目标粒子群优化
陈万芬,王宇嘉,林炜星
(上海工程技术大学 电子电气工程学院,上海 201620)
多目标进化算法已被应用于许多现实世界中的复杂优化问题,但是当将其应用于求解耗时的多目标优化问题时,优化过程通常需要进行大量的适应度函数评估才能找到Pareto最优解。为了解决计算量大的多目标优化问题,代理辅助进化算法(Surrogate Assisted Evolutionary Algorithms, SAEAs)被广泛采用[1],以便采用计算廉价的代理模型来代替昂贵的实际适应度函数评估。
代理模型通常指代替更复杂耗时的数值分析的近似数学模型,任何具有预测能力的模型都可以被用作代理模型[2-7]。提高模型的准确度以及模型管理是SAEAs领域中目前急需解决的问题。模型管理又称为加点准则,通过代理模型产生新的样本点,达到提高代理模型精度的目的[8]。建立有效的代理模型,并使用加点准则的模型管理策略加速收敛和改善优化中的多样性,对提高代理模型的预测能力具有重要意义[9]。
模型管理是SAEAs中更新代理模型的重要步骤,国内外研究人员陆续提出多种加点准则,例如改善期望准则(Expected Improvement, EI)[10]、改善概率准则(Probability of Improvement, PI)[11]、最小化代理模型预测准则(Minimize Surrogate Prediction, MSP)[12]、置信下界准则(Lower Confidence Bound, LCB)[13]等。文献[14]使用EI准则来选择精度较高的候选解以更新代理模型,使算法在评估昂贵或数量有限的多目标优化问题上表现出较好的性能。文献[15]建立代理模型后,为每个子问题计算EI值,并求解EI的最大值,以减少问题的计算复杂性和适应度函数评估的数量。文献[16]使用高斯过程代理模型的LCB准则来选择适应度较好的后代,用以解决进化多目标优化问题。文献[17]提出代理辅助的模拟退火算法,该算法通过使用均方根误差计算得出代理模型的准确性来评估种群中的个体,提高了代理模型的精度并减少了计算成本。这些基于单一加点准则的代理模型辅助多目标优化算法的效率虽有所提高,但在每次迭代中均只添加了1个新增样本点来更新代理模型,导致整个Pareto 前沿无法在一次迭代中得到充分的探索。
基于以上问题,文献[18]使用EI准则和PI准则选择要重新评估的个体进行多目标优化,获得了当前近似Pareto解集,结果表明该方法优于NSGAII算法。文献[19]提出一种多目标加点准则,该准则将加点采样视为一个双目标问题,同时使预测的适应度和其方差最小。该方法选择第一个和最后一个非支配前沿的解作为新的加点样本,使得所提出的多目标加点准则对于高维优化问题有较好的优化效果。上述算法能够在一次迭代中同时添加多个样本点,提高优化效率,但是其较少关注集成模型提供的不确定信息。已有研究表明,集成模型成员输出的方差不确定性信息对于模型管理是有效的[20-21],因此代理模型中的不确定信息应得到更多的关注。
为了建立精度和效率都较高的代理模型,提高适应度近似的准确性,增强代理模型的预测性能,本文提出了组合加点准则的代理辅助多目标粒子群优化算法。该算法将Kriging模型与径向基函数网络模型加权集成为预测稳定性较强的异构集成模型,利用集成代理提供的不确定性信息提高模型预测能力,并使用组合加点准则进行模型管理,实现了勘探与开发之间的平衡。
1 多目标粒子群优化算法及代理模型
1.1 多目标优化问题
通常情况下,多目标优化问题(Multi-Objective Optimization Problems,MOPs)包含多个相互冲突的目标。以最小化目标为例, MOPs可以被描述为
(1)
式中,m是目标函数的数目;x是决策变量;fi(x)是第i个目标函数。若决策变量x1完全支配另一个决策向量x2,则表示为x1x2,所需满足的条件如式(2)所示。
(2)
在MOPs中,当一个解不受任何其他解支配时,则可以称其为Pareto最优解。在搜索空间中,将所有Pareto最优解的集合形成的权衡曲面称为Pareto前沿。
1.2 粒子群优化算法
粒子群优化(Particle Swarm Optimization,PSO)算法是一种模拟鸟类群体智能行为的随机搜索算法[22]。该算法中,将每只鸟都视为一个粒子,粒子与粒子之间通过相互协作和信息共享完成寻优过程,进而找到符合优化问题的最优解。PSO算法的位置和速度更新式为
vi(k+1)=w×vi(k)+c1r1(pbesti-xi(k))+
c2r2(gbest-xi(k))
(3)
xi(k+1)=vi(k+1)+xi(k)
(4)
式中,i=1,2,…,N是粒子的个数;N表示种群的大小;vi(k)表示粒子i在第k维的速度;xi(k)表示粒子i在第k维中的位置;w是惯性权重;常数c1和c2是加速系数,其中c1表示向自身学习的能力,c2表示粒子向整个种群学习的能力;r1和r2是均匀分布在[0,1]中的随机值;pbesti表示粒子i所经历的最优位置,其所在的和项表示向自身学习的机制;gbest表示种群中最好粒子的位置,其所在的和项表示粒子向整个种群学习的机制。
1.3 代理模型
代理模型是真实函数的近似值,可用来构建更为简单且计算成本更低的模型,主要包括Kriging模型、径向基函数网络(Radial Basis Function Network,RBFN)模型、多项式回归模型、支持向量回归模型等。下面主要介绍本文使用的Kriging模型和RBFN模型。
1.3.1 Kriging模型
Kriging也被称为高斯过程(Gaussian Process)[23]。与其他代理模型相比,Kriging模型不仅能给出估计值,还可以生成估计值的均方误差,用于指导添加新的采样点,以更新代理模型并提高模型的准确性。Kriging模型本质上是一种插值模型,将目标函数视为高斯随机过程的具体实现,表示为
Y(x)=f(x)+Z(x)
(5)
式中,f(x)为全局趋势,代表近似函数Y(x)的数学期望;Z(x)为局部偏差,数学期望为0。
1.3.2 RBFN模型
径向基函数(Radial Basis Function,RBF)方法[24]是一个实值函数,其值取决于从输入x到神经元中心c的距离。RBF的典型选择包括:线性函数、三次函数、多二次函数或高斯函数。
RBFN通常具有3层,即包含识别函数的输入层、具有非线性RBF激活函数的隐藏层以及线性输出层。网络的输出为
(6)
式中,φ(x)表示RBFN的输出结果;N是样本点大小;φ(‖x-ci‖)表示径向基函数,为了使RBFN模型适应特定任务,需要微调3个参数:权重wi、中心向量ci和RBF宽度参数βi。
2 组合加点准则的代理辅助多目标粒子群优化
2.1 算法框架
目前,大量的代理模型方法被用于解决许多不同适应度形态特性的优化问题,其中RBFN模型在训练数据小的情况下,对于各类非线性度不同的问题表现最好。随着搜索维度以及规模的增加,RBFN模型也能有较好的表现。Kriging模型作为一类统计学习模型,适合于捕捉复杂优化问题的全局场景,并能获得与RBFN模型相媲美的结果。为了能够快速有效地解决不同形态的优化问题,本文提出了组合加点准则的代理辅助多目标粒子群优化算法。该算法将Kriging模型与RBFN模型加权集成为预测稳定性较强的异构集成模型,利用EI准则和MSP准则结合的组合加点准则在每一次迭代中同时添加多个样本点更新代理模型,其算法流程图如图1所示。

图1 组合加点准则的代理辅助多目标粒子群优化算法流程图
首先对目标函数进行采样,使用采样的样本点训练由Kriging模型和RBFN模型组成的异构集成模型;然后,使用实际目标函数评估组合加点准则产生的多个新样本点。将包括新数据样本点的扩展训练集用于代理模型的训练,以此更新代理模型;最后,使用多目标粒子群优化算法对异构集成模型进行优化,得出Pareto最优解集。
组合加点准则的代理辅助多目标粒子群优化算法的具体步骤如下:
步骤1初始化种群。基于样本点数据库进行种群的初始化,通过最优拉丁超立方采样(Optimal Latin Hypercube Sampling,OLHS)[25]方法从决策变量空间内抽取样本点X,并将这些样本点用于评估目标函数值Y,得出样本点对应的优化目标样本数据集,并使用[X,Y]作为训练数据;
步骤2初始化代理模型。根据种群中粒子的信息,使用样本点数据集初始化两个代理模型,并训练Kriging模型和RBFN模型;
步骤3构建异构集成模型。根据加权平均法求出两个代理模型的权重,其中权重由代理模型的均方根误差得出。通过模型预测误差来调整权重大小,预测误差较小的模型,其权重较大[26];
步骤4代理模型的更新。对构造的异构集成模型进行误差分析,在不满足代理模型精度要求时,使用EI准则和MSP准则结合的加点准则来增加样本点,重新建立异构集成模型;在满足代理模型精度要求时,利用异构集成模型对更新的候选解进行评估,选出预测结果最好的粒子进行精确适应度函数评估;
步骤5利用更新后的异构集成近似模型计算各个粒子的适应度值,并将非支配解存储到外部存档中;
步骤6种群的更新。根据多目标粒子群优化算法更新种群中各个粒子的位置和速度,重新计算各个粒子的适应度值,更新个体极值、全局极值以及外部存档;
步骤7终止条件的判断。以所得粒子是否接近全局最优解作为收敛条件,若未达到收敛,对种群进行更新,并返回步骤5;若收敛,则得出Pareto 最优解集。
2.2 模型管理
2.2.1 EI准则


(7)

(8)
式中,σ2是方差;p是单位向量;R是样本点x的相关函数。通过求解maxEI(x)的子优化问题,可得出新的样本点x*。
2.2.2 MSP准则
在代理辅助优化算法中,最小化代理模型预测准则是最简单、最直接,也是最早被采用的方法,其原理是直接在代理模型上寻找目标函数的最小值,然后加入样本数据集来更新代理模型。子优化问题的数学模型为

(9)

2.2.3 组合加点准则
EI准则理论上是一种全局优化算法,但优化后期收敛速度较慢。MSP准则通常用于局部优化,但在优化空间十分复杂或者选取初始样本点较少时,其容易陷入局部最优而无法找到全局最优解。本文将EI准则和MSP准则结合成组合加点准则,该方法既能克服单一加点准则的缺陷,还可以加快收敛速度,能够在一次迭代中同时获得多个样本点,用于更新代理模型,提高模型的准确性和优化效率。组合加点准则的模型管理过程如图2所示。

图2 组合加点准则的模型管理过程
图2中,本文使用的异构集成模型由具有不同输入函数的Kriging模型和RBFN模型组成。集成成员输出的预测方差可估计适应度函数预测中的不确定性程度,用于模型管理。在优化中,集成模型代替了真实的目标函数,以评估由多目标进化算法找到的候选解,而组合加点准则用于计算这些解的最优值。
3 实验分析
本文使用具有不同复杂度的数值函数DTLZ[28](除DTLZ5和DTLZ6外)来测试所提出的方法,算法比较结果如表1所示。

表1 多种算法比较
为了减少随机误差的影响,每个测试函数都进行了10次实验。本文所使用的多目标粒子群优化算法的参数设置为:种群大小为100,领导者大小为100,变异概率为0.1,变异扰动为0.5,迭代次数为100。
3.1 测试函数
本文选择的数值测试函数是DTLZ1、DTLZ2、DTLZ3、DTLZ4和 DTLZ7,这些函数具有不同程度的复杂性,可有效说明所提方法的适用性。测试函数的性能如表2所示。

表2 测试函数特性
3.2 性能指标
本文使用3个评价指标来评估算法的性能,分别是世代距离(Generational Distance,GD)[31]、间距(Spacing,SP)[32]和超体积(Hyper-Volume,HV)[33]。GD指标和SP指标分别用来评价算法的收敛性和多样性。HV指标提供了一组非支配解的收敛性和多样性的组合信息,并且HV值越高,非支配解的质量越好。在本文中,沿着Pareto前沿采样了1 000个均匀分布的参考点组成参考集以计算GD指标、SP指标和HV指标。
3.3 实验结果与分析
假设目标函数的计算在实验过程中是昂贵的,M和D分别代表所有测试实例中目标函数的数量和决策变量的数量,算法参数设置如表3所示。对于所有比较算法,独立运行次数均为10次,且在每次运行中,初始训练数据都是新生成的。

表3 算法参数设置
为了将本文所提算法与NSGAIII、OMOPSO、HE-OMOPSO和HE-OMOPSO-EI进行比较,所有实验均使用相同的初始种群。在10次实验中,记录每种算法的实际仿真成本数量以及通过这些方法获得的非支配点。针对每次实验计算GD指标、SP指标和HV指标,其均值和标准偏差如表4~表7所示,实验结果如图3所示。

表7 HV的标准偏差
实验结果表明,与NSGAIII、OMOPSO、HE-OMOPSO和HE-OMOPSO-EI相比,本文所提方法在测试函数DTLZ1、DTLZ2、DTLZ3和DTLZ7上表现较好。从图3(a)~图3(c)中可以看出,本文所提方法在真实Pareto前沿上的分布性和均匀性与NSGAIII、OMOPSO、HE-OMOPSO和HE-OMOPSO-EI等算法效果相似,但是所提方法与传统方法相比使用了更少的适应度函数评估次数,也获得了更好的近似值;与HE-OMOPSO和HE-OMOPSO-EI相比,所提方法的模型准确率更高。从图3(d)中可以看出,所提方法在真实Pareto前沿上的分布性和均匀性与HE-OMOPSO和HE-OMOPSO-EI相比效果相似,而与NSGAIII和OMOPSO相比收敛性较差,这是由于测试函数DTLZ4的复杂性使得代理模型难于近似真实函数,导致算法性能变差。从图3(e)中可以看出,所提方法在分布性和多样性上比HE-OMOPSO和HE-OMOPSO-EI好,除了可生成更接近真实的Pareto前沿的点外,还生成了沿其分布更好的点。
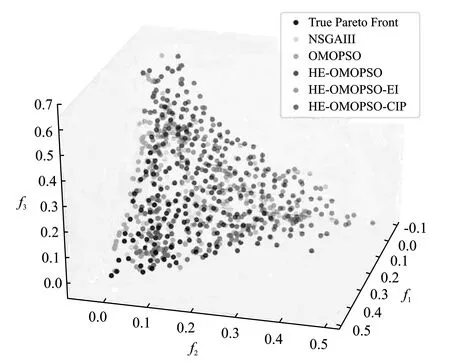
(a)
本文以测试函数DTLZ2为例,分别从GD、SP和HV共3个性能指标来说明算法的有效性。从图4(a)和图4(b)中可以看出,随着迭代次数的增加,本文所提方法能较快地收敛,并且解集分布也较均匀,算法在收敛性和多样性方面取得了较好的效果,这是因为所提方法使用组合加点准则用于模型管理,而在代理模型中又引入MSP准则用于局部搜索优化,提高了算法的多样性。从图4(c)中可以看出,随着迭代次数的增加,HE-OMOPSO-CIP的HV值虽然多次陷入局部最优,但是能够很快跳出,然后继续迭代到HV值收敛。这是因为EI准则被用于全局搜索优化,而MSP准则被用于局部搜索优化,两者相结合,加快了收敛速度。从图4(d)中可以看出,随着评估次数的增加,HE-OMOPSO-CIP能较快地收敛,在达到相同的收敛指标时,OMOPSO的评估次数是本文所提算法的10倍。
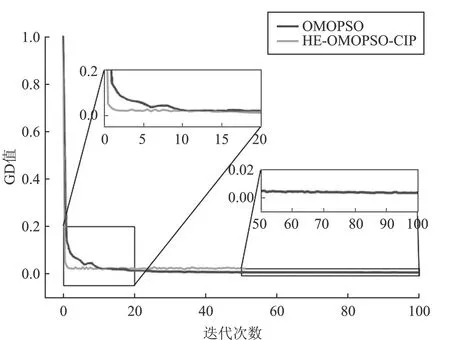
(a)
由于测试函数DTLZ4和DTLZ7的Pareto前沿具有多个局部最优解,因此适用于测试算法的收敛性能。从表4和表5中可以看出,在测试函数DTLZ4和DTLZ7中,本文所提方法与HE-OMOPSO和HE-OMOPSO-EI相比取得了较小的GD值,证明EI准则和MSP准则都能够提高非支配解的质量,将两者结合起来可以进一步提高算法的收敛性,从而提高算法性能;而异构集成模型中的Kriging模型可以使预测误差减小,增强全局搜索能力,进而提高算法的收敛性。HE-OMOPSO-CIP在测试函数DTLZ3中取得了较小的GD值和SP值,说明该算法能够获得收敛良好且分布均匀的最优解。使用组合加点准则可以避免算法陷入局部最优,而异构集成模型中的RBFN模型可以增强局部搜索能力,提高算法的多样性。在DTLZ2函数中,所提方法取得了较小的SP值,说明算法获得的非支配解在真实的Pareto前沿上分布较均匀,算法的多样性较好。
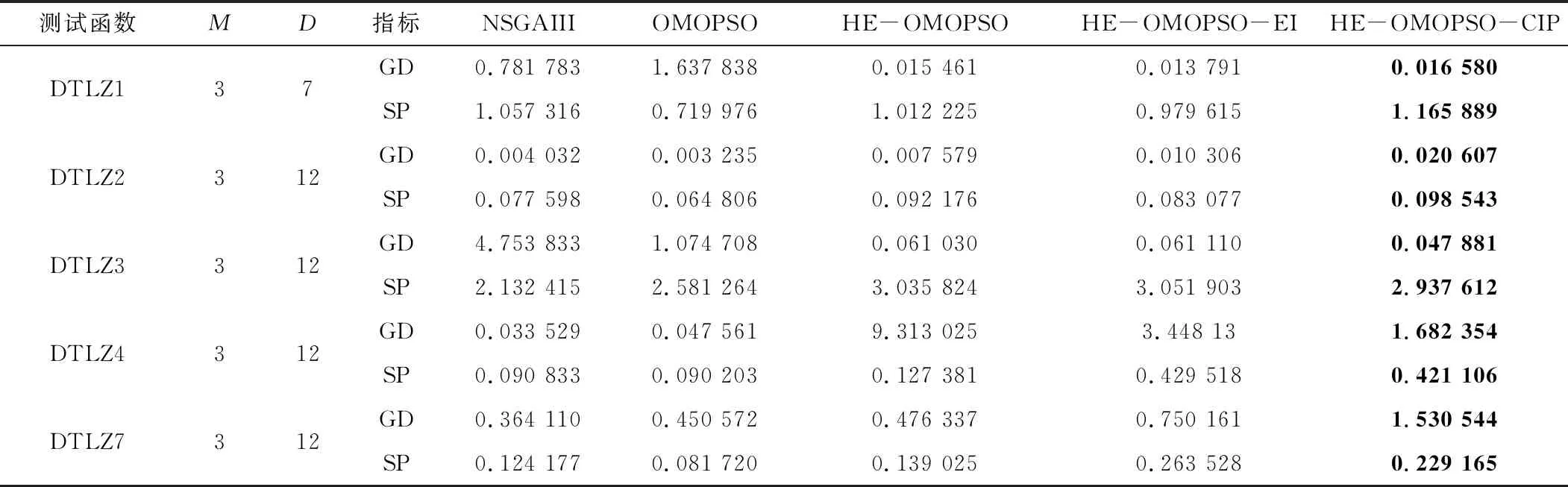
表4 GD和SP的平均值
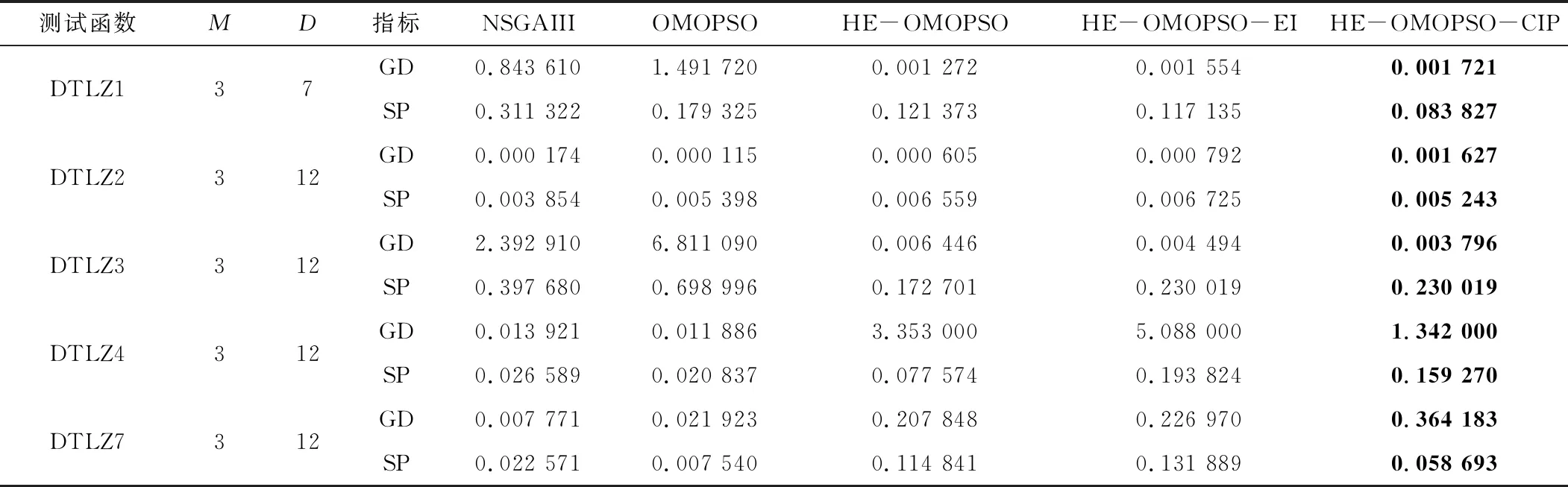
表5 GD和SP的标准偏差
从表6和表7中可以看出,本文方法在全部测试函数中的HV值与其他算法相当或更好,说明HE-OMOPSO-CIP获得的HV值与所比较的算法相比,算法的收敛性和多样性都较好,也表明近似Pareto前沿解集有较好的收敛性和多样性。在测试函数DTLZ2上,所提方法的HV值比单一加点准则和无加点准则的HV值更好,说明所提方法能够在勘探与开发之间实现更好的平衡。所提方法在测试函数DTLZ4中获得的标准偏差几乎为0,其均方误差也接近于0,说明所提方法在DTLZ4中优于其他算法。上述结果证明组合加点准则可以根据适应度估计值和方差来评估解的质量,提高代理模型的准确性和预测能力,从而获得近似Pareto最优解集。

表6 HV的平均值
4 结束语
本文提出组合加点准则的代理辅助多目标粒子群优化算法来解决耗时的多目标优化问题,并将所提方法与其他基于代理模型的方法进行了基准测试函数的比较。实验结果表明,对于高维问题,组合加点准则的代理模型充分利用了异构集成模型的预测能力,较好地平衡了算法的多样性和收敛性,能够有效优化计算量大的多目标优化问题。

