矩阵方程有解判别

◎祁明远 李俊澳 糜涵 魏聪龙 魏俊潮

(1.扬州大学数学科学学院，江苏 扬州 225002；2.扬州职业大学数学学院，江苏 扬州 225002)

2021年度扬州大学科创基金“同解矩阵方程组对广义逆矩阵的刻画”(项目编号：X20210240)

一、引言

在线性代数的教与学中，矩阵的初等变换可以作为这门课的主线，这里有两个原因，首先，无论是求可逆矩阵的逆矩阵、矩阵的秩、向量组的秩与极大无关组，还是求线性方程组的解、矩阵的特征值和特征向量以及用正交变换等方法化二次型为标准型等都与矩阵的初等变换息息相关，这也说明矩阵的初等变换在教学中具有举足轻重的地位；其次，矩阵初等变换的有关知识点具有易于理解、难度不大、容易上手的特点，能够激发同学们的学习兴趣，老师在授课时也相对轻松，容易讲清楚.因此，学好了矩阵的初等变换基本就能学好线性代数，进而能够掌握线性代数的基本知识与相关应用.

本文中的所有矩阵都是实矩阵，这也是线性代数的教学基于实数域的原因.近年来利用矩阵方程的解的表示形式来研究矩阵广义逆的性质是矩阵理论研究中的一种新形式，如文献[1]建立了EP矩阵与方程的解之间的等价关系；文献[2]研究了群可逆矩阵与矩阵方程的解的相互联系；文献[3]探究了EP矩阵与相关矩阵方程在给定集合中有解之间的等价刻画;除此还有更加系统的研究.受这些研究的影响，本文通过对线性代数中最为基本的矩阵初等变换的研究，探究矩阵的相关性质，并利用这些性质，去探讨线性方程组有解的等价刻画，从而给出线性方程组在有解时其一般解的显式表示.

二、主要结果

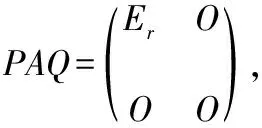
注2对于引理1中m阶可逆矩阵P与n阶可逆矩阵Q的求法，可以利用矩阵的初等变换加以求解，其中对矩阵A进行初等行变换，相当于对矩阵A左乘m阶初等矩阵；对矩阵A进行初等列变换，相当于对矩阵A右乘n阶初等矩阵，具体如下：

引理1引出了下面的几个命题.

命题3设A是m×n矩阵，则存在n×m矩阵B，使得A=ABA且r(B)=r(A).

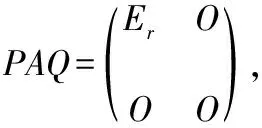
则有r(B)=r=r(A)，并且

推论4设A是m×n矩阵，则存在n×m矩阵C，使得A=ACA,C=CAC且r(C)=r(A).

证明：由命题3可知，存在n×m矩阵B，使得A=ABA且r(B)=r(A).不妨选取C=BAB，则有ACA=A(BAB)A=(ABA)BA=ABA=A,

CAC=(BAB)A(BAB)=B(ABA)BAB=BABAB=BAB=C.

注意到r(C)=r(BAB)≤r(B)=r(A)=r(ACA)≤r(C)，因此有r(C)=r(A).

推论5设A是m×n矩阵，则存在m阶幂等矩阵F及n阶幂等矩阵G，使得A=FAG且r(F)=r(A)=r(G).

证明：由推论4可知存在n×m矩阵C，使得A=ACA,C=CAC且r(C)=r(A)，因此有

A=ACA=A(CAC)A=(AC)A(CA).不妨选取F=AC,G=CA，则我们有

A=(AC)A(CA)=FAG，

F2=(AC)(AC)=(ACA)C=AC=F，则F为m阶幂等矩阵，

G2=(CA)(CA)=C(ACA)=CA=G，则G为n阶幂等矩阵.

又由于r(F)=r(AC)≤r(A)=r(ACA)=r(FA)≤r(F)，所以r(F)=r(A).

同理可证r(G)=r(A)，从而我们有r(F)=r(A)=r(G).

命题6设A是m×n矩阵，β是m维列向量，则线性方程组AX=β有解当且仅当存在n×m矩阵B，使得β=ABβ.

证明：“⟹”假设线性方程组AX=β有解，不妨设X=X0是其一个解，则有AX0=β.

由命题3可知存在n×m矩阵B，使得A=ABA且r(B)=r(A).于是我们有

ABβ=AB(AX0)=(ABA)X0=AX0=β.

“⟸”假设存在n×m矩阵B，使得β=ABβ，则X=Bβ为AX=β的一个解.

从而线性方程组AX=β有解.

命题7设A是m×n矩阵，β是m维列向量，则线性方程组AX=β有解当且仅当存在m阶幂等矩阵F，使得A=FA，β=Fβ且r(F)=r(A).

证明：“⟹”假设线性方程组AX=β有解，不妨设X=X0是其一个解，则有AX0=β.

由推论5可知存在m阶幂等矩阵F，使得A=FA且r(F)=r(A).于是我们有

Fβ=F(AX0)=(FA)X0=AX0=β.

“⟸”假设存在m阶幂等矩阵F，使得A=FA，β=Fβ且r(F)=r(A).则

推论8设A是m×n矩阵，β是m维列向量，则线性方程组ATAX=ATβ一定有解.

证明：由推论5可知，存在n阶幂等矩阵G，使得A=AG且r(A)=r(G).从而我们有

ATA=GT(ATA)，ATβ=(GTAT)β=GT(ATβ).

注意到r(GT)=r(G)=r(A)=r(ATA)且GT是幂等矩阵，因此由命题7可知线性方程组ATAX=ATβ一定有解.

推论9设A是n阶矩阵，则存在n阶矩阵C，使得AT=ATAC.

证明：分别取β=βj，其中βj是第j个分量为1，其余分量为0的n维列向量，j=1,2，…,n.

由推论8可知分别存在n维列向量αj，使得ATAαj=ATβj，j=1,2，…,n.

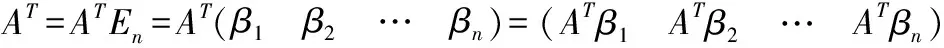
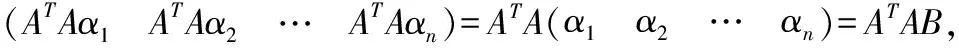
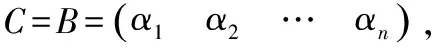
从而我们有AT=ATAC.

推论10设A是n阶矩阵，则存在n阶矩阵D，使得A=DATA.

证明：该推论其实是推论9的直接结果，由推论9可知，存在n阶矩阵C，使得AT=ATAC，两边同时取转置，可得A=CTATA，不妨选取D=CT，从而可得A=DATA.

命题11设A是n阶对称矩阵，则存在n阶矩阵W，使得A=A2W,AW=WA,W=W2A.

证明：由于A是n阶对称矩阵，从而有AT=A，因此由推论9与推论10可知存在n阶矩阵C和n阶矩阵D，使得A=AT=ATAC=A2C，A=DATA=DA2，即A=A2C=DA2，于是我们有

AC=(DA2)C=D(A2C)=DA，

ACA=DA2=A，

ADA=A2C=A.

不妨取W=DAC，则可得

AW=A(DAC)=(ADA)C=AC=DA=D(ACA)=(DAC)A=WA，

A2W=A(AW)=A(WA)=A(DAC)A=(ADA)CA=ACA=A，

W2A=W(WA)=W(AW)=W(ADAC)=WAC=(DAC)AC=DAC=W.

命题12设A是m×n矩阵，β是m维列向量，若线性方程组AX=β有解X=η，则AX=β的一般解由下式给出：

(1)X=η+δ-BAδ，其中δ为任意的n维列向量，B为n阶矩阵且满足A=ABA.

证明：由于A(η+δ-BAδ)=Aη+Aδ-ABAδ=β+Aδ-Aδ=β，因此公式(1)是线性方程组AX=β的解.

现设X=X0是AX=β的任意一个解，则AX0=β.不妨选取δ=X0-η，则有

BAδ=BA(X0-η)=BAX0-BAη=Bβ-Bβ=0，

因此X0=η+(X0-η)-BAδ=η+δ-BAδ，这说明AX=β的任意一个解都具有公式(1)的形式，因此AX=β的一般解由公式(1)给出.

三、结语

本文借助于矩阵分解理论，通过对线性代数中最为基本的矩阵的初等变换的研究，得到了矩阵的相关性质，探讨了矩阵方程组AX=β的一般解的显式表示，这是研究矩阵方程相容性的形之有效的方法.