用于求解民船装载问题的R-CS-PSO 混合改进算法
赵小康, 卢厚清
(1.陆军工程大学, 江苏 南京 210014; 2. 31151 部队, 江苏 南京 210016)
0 引言
装载问题属于离散组合优化问题, 有多个不同类型的民船(背包)、多种需要装载的货物(物品)和多重约束条件,目标函数不唯一,且解空间是离散点的集合,可以将其归为多约束背包问题(MKP,Multi-constrained Knapsack Problem)。
MKP 问题是一个NP-Hard 问题, 对于此类问题,国内外很多专家都进行了研究, 目前的解决方法主要分为两类:一类是精确的求解方法,如枚举法、动态规划方法、回溯法和分支定界法等;另一类是用启发式算法来求解,如贪婪算法、遗传算法、蚁群优化算法、模拟退火算法、粒子群优化算法等;近年来随着智能优化算法的不断发展,布谷鸟搜索算法、鸡群优化算法、哈里斯鹰优化算法等新的优化算法也被用于解决背包问题。
采用精确的求解方法虽然原理简单、容易理解、使用方便,在较小规模的问题上该方法可以得到精确解,取得不错的计算效果; 但计算时间和计算复杂度会随着物品数量增加呈指数增长,随着背包变大和物品数量的增多,用来求解背包问题会浪费大量时间,占用大量存储空间。使用智能优化算法求解此类问题, 面对不断复杂化和规模变大的问题, 可以在保持快速收敛计算的同时寻找到一个比较精确的解,在实际应用取得较好的计算效果,对于生产生活具有重要意义。
通过查阅书籍和阅读文献可以知道, 使用粒子群优化算法来解决类似0-1 背包类的离散优化问题, 通过向上或向下取整的方式将实数的符号和小数部分去掉,直接转化为正整数是可行的, 且用该方式求解的速度和解的质量要优于大多数其他智能优化算法[1],本文我们借助此思想,将布谷鸟搜索算法和粒子群算法结合起来,对算法进行混合改进来求解此问题。
1 粒子群优化算法
粒子群优化(Particle Swarm Optimization,PSO)算法,又称为微粒群优化算法, 是1995 年美国心理学家Kennedy 和电气工程师Eberhart 通过观察鸟群觅食行为,发现其有一定的规律, 进而总结此类行为规律提出的群体智能优化方法[2]。由于算法概念简明、易于实现,在解决优化问题领域具有优越性, 出现后迅速得到了各国研究者的认可,目前已被用于多个领域。
1.1 算法原理
该算法主要将将鸟群的栖息地鸟巢抽象的看作空间中的解,每只鸟相当于抽象空间中的一个粒子,每个粒子的运动轨迹都是在本身历史最好位置和所有粒子当前最优位置的影响下,不断寻找全局最优解的过程[3]。 在该算法模型中,每个粒子都是可行解空间中的一个可行解,都有一个被优化函数目标所决定的适应值, 每个粒子的运动状态都使用一组速度和位置向量来进行描述。 在初始化粒子种群中,各个粒子在空间中进行不规则的运动,运动过程中,每个粒子都会去寻找本身的最优位置,而整个粒子种群会寻找整个种群的最优位置, 每个粒子的运动都会受到当前自身最优位置和整个种群当前最优位置的影响,经过不断的迭代后,找到问题的最优解[4]。
1.2 数学模型
该算法的数学模型描述如下:规模为M 的粒子群在一个N 维的搜索空间中以一定的初速度进行不规则运动,xi=(xi1,xi2, …,xim) 表示第i 个粒子的位置;vi=(vi1,xi2,…,vin)表示第i 个粒子的速度;pi=(pi1,pi2,…,pin)表示第i个粒子经过n 次迭代后所经过的最佳位置, 也称为个体最优(pbest,personal best);g=(g1,g2,…,gn)表示所有粒子经过n 次迭代后所搜寻到的最佳位置, 也称为全局最优(gbest,global best)。
在粒子群优化算法中粒子位置和速度的更新公式如下:
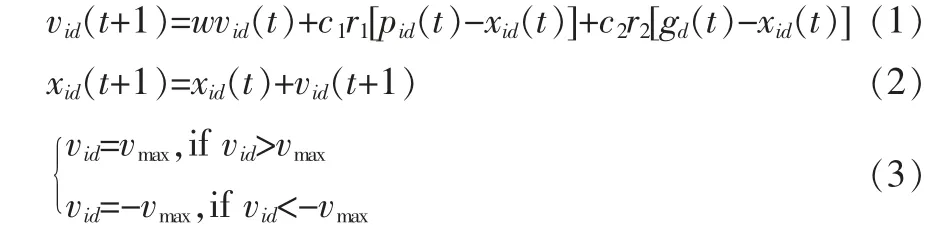
关于该公式中:i∈[1,M],d∈[1,N];vid表示粒子的速度,xid表示粒子的位置;w 表示惯性权重因子(inertia weight);c1、c2为加速常数(acceleration constants),也称为学习因子;r1、r2为在[0,1] 之间均匀分布的随机数;pbest表示个体最优解,gbest 表示整个种群的全局最优解。
式(3)中,对粒子的速度vi进行了有关约束,将速度限制在[-vmax,vmax]这一区间;如果vmax过大,粒子就会速度过快,进而飞越最优解;如果vmax太小,粒子就会在很小的范围内运动,难以进行整体搜索找到全局最优解。
从式(1)可以看出,粒子群优化算法的速度更新公式由三个部分共同构成[5-6]。 第一部分表示粒子的历史速度对当前速度的影响, 该部分起到了平衡全局和局部搜索的作用, 参数w 是为了平衡粒子的局部搜索能力和扩大对全局的搜索能力而引入的惯性系数。 第二部分反映粒子本身认知模式(cognition modal)影响,表示粒子自身的历史最优位置对个体速度更新的影响, 使粒子可以在更大范围内搜索求解,以免只取得局部最优解。第三部分反映社会模式(social modal)对粒子的影响,表示种群中各个粒子受整体中最好位置的影响,并向其靠拢,体现粒子之间进行信息共享、互相学习、互相影响。 在三部分共同作用之下,粒子群基于信息共享,根据历史经验,在当前个体最优位置的基础上不断变化调整, 以此来寻找整个问题的最优解。
1.3 算法步骤和流程
粒子群优化算法的基本步骤为:
Step1:设置算法有关参数,生成初始种群,生成粒子初始的速度和位置;
Step2:计算各个微粒的适应度函数值;
Step3:计算并更新每个微粒的最好位置,找出每个粒子自身的最优位置pbest 和整个种群的最优位置gbest;
Step4:按照公式(1)更新各个微粒的速度,按照公式(2)更新各个微粒的位置;
Step5: 比较种群中每个微粒当前目标值与其pbest 的目标值, 如果当前目标值更优,则用微粒的当前位置和目标更新其pbest;
Step6: 比较当前所有pbest 和gbest 的 值, 更 新gbest;
Step7: 若未达到终止条件,转Step4;若达到终止条件, 则输出gbest 及其目标值并停止算法。根据基本步骤,绘制流程图见图1。
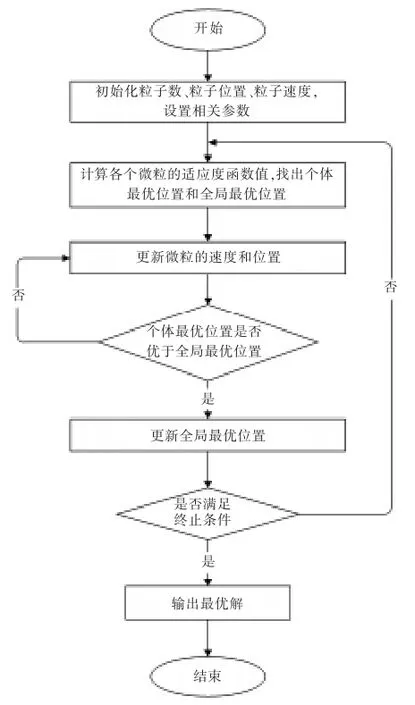
图1 粒子群优化算法基本流程图
2 布谷鸟搜索算法
布谷鸟搜索(Cuckoo Search,CS)算法,又称杜鹃搜索, 于2009 年由剑桥大学Xin-She Yang 教授和S. Deb在研究杜鹃孕育雏鸟行为的基础上, 结合部分鸟类和昆虫在飞行过程中具有Lévy 飞行特点提出的一种智能优化优化算法[7]。 该算法提出后,由于其简单的结构和高效的性能迅速成为研究的热点,被广泛应用到诸多领域。
2.1 算法原理
布谷鸟是一种神奇的鸟类,其雌鸟不会自己孵蛋,而是使用侵略性手段占据别的鸟类的巢穴让其他鸟类帮助其孵蛋,并且鸟巢内一般还会有其他鸟类产下的蛋。有时候布谷鸟会将自己产下的鸟蛋让其他鸟类一起孵化;有时候布谷鸟为了提高自己产生蛋的孵化概率会将鸟巢内原有的鸟蛋推出巢内;当然,布谷鸟产下的蛋也会被鸟巢主人发现而毁坏或者放弃原有鸟巢重新搭筑巢穴。 在该算法模型中, 布谷鸟产蛋的每个鸟巢相当于解空间的一个可行解,有一个被优化函数目标所决定的适应值,可以用解空间的一个位置来描述,而该位置以符合Lévy 飞行的方式进行变化。
2.2 数学模型
考虑建立算法数学模型的可行性, 布谷鸟的繁殖行为可以理想化概括为以下几点:
(1) 每只布谷鸟每次随机选择一个宿主鸟巢产下一枚蛋,选择的鸟巢为一个可行解。
(2)在任意选择的所有鸟巢中,能够被保留下来,并顺利进入下一代的被认为是最好的。
(3)能够被选择产蛋的鸟巢的总数量是确定的,鸟巢原主人发现布谷鸟蛋的概率为pα,其中pα∈[0,1],若被发现,则该鸟巢被淘汰。
(4)布谷鸟按照Lévy 飞行的方式寻找下一个鸟巢并产蛋,代替被淘汰的鸟巢。

布谷鸟搜索算法的具体求解过程如下: 在确定空间里随机产生一定规模数量的鸟巢并产蛋, 选择当前最好的鸟巢并存储,通过步长公式变换鸟巢新位置并产蛋;如果布谷鸟蛋被其他鸟类发现,则代表该鸟巢被淘汰,需更新鸟巢位置,寻找新的鸟巢;寻找最好的鸟巢位置是一个不断循环迭代的过程, 每次迭代都要计算当前所有剩余鸟巢的位置;不断重复上面的求解过程,就可以找到鸟巢的最好位置,也就是问题的最优解。
2.3 算法步骤和流程
布谷鸟搜索算法的基本步骤为:
Step1:种群初始化,随机选择n 个鸟巢产蛋,生成初始解集;
Step2:计算每个鸟巢的目标函数值,获得初始全局最优解;
Step3:通过Lévy 飞行更新鸟巢位置,获得新解;
Step4:由于布谷鸟蛋可能被发现,根据淘汰机制和概率淘汰部分解;
Step5:对现有鸟巢和上一代剩余鸟巢进行对比,将较好的位置保留下来,更新全局最优解;
Step6:判断迭代条件,若未达到终止条件,转Step3;
Step7:输出全局最优解。
根据基本步骤,绘制流程图见图2。

图2 布谷鸟搜索算法基本流程图
3 R-CS-PSO 混合算法
每种智能算法都有优点和缺点,没有一种智能算法能完美的解决所有问题,于是人们在实际使用过程中会考虑对已有的智能算法进行优化改进,在保持算法本身优点的同时根据需要克服不足,以达到更好解决问题的效果。 目前,研究领域对于粒子群算法改进和布谷鸟搜索算法改进都研究的比较多, 也取得了很好的应用效果,解决了很多实际领域的问题,本文在查阅大量文献基础上,分析两种算法的优缺点,将两种算法混合起来,并引入随机变化的惯性系数,进一步增进算法的活跃度,以达到取长补短的效果。
3.1 改进思想
粒子群优化算法具有搜索速度快、 寻优效率高的特点, 且粒子可以根据历史经验并利用信息共享机制进行位置更新, 但在计算后期大多数粒子容易集中于一个最优解附近,出现早熟和局部最优。布谷鸟搜索算法中鸟巢采用Lévy 飞行随机游走的方式进行更新,可以在丰富种群多样性的同时让搜索范围扩大, 该算法中使用的鸟巢淘汰机制,也可以使算法跳出局部最优,进而在全局内进行较好的搜索。 R-CS-PSO 算法针对两种算法的不同特点,将两种算法的优点结合在一起,有效克服其不足,将布谷鸟搜索算法中鸟巢采用Lévy 飞行进行变化的机制引入粒子群优化算法, 同时也将淘汰机制的理念也引入粒子群优化算法, 不仅有助于粒子在局部范围进行精细搜索,找到更优的解;而且增加了粒子的活力,让粒子跳出局部进行更大范围搜索,进而搜索得到全局最优解。
在算法改进的过程中, 考虑粒子群优化算法中是为了平衡全局和局部搜索能力而引入的惯性系数, 在搜索早期要求有较大速度,也就是较大的,便于在全局内进行快速搜索;在搜索的后期要求速度减缓,也就是较小的,算法可以快速收敛找到更精确的解; 因此提出一种分段随机的调整策略,使在逐渐缩小的同时又随机变化,进一步增加粒子的活力,丰富种群的多样性。

式中:t 表示当前迭代次数;Ndt为设置的最大迭代次数;r0为介于[0,1]之间均匀分布的随机数;wmax为通过经验和仿真实验设置的最大惯性权重系数;wmin为通过经验和仿真实验设置的最小惯性权重系数。
3.2 算法步骤
根据改进思想,设计随机布谷鸟粒子群(R-CS-PSO)混合算法的基本运行步骤如下:
Step1: 程序初始化, 设置R-CS-PSO 算法的相关参数。 主要包括:粒子个数M,最大迭代次数Ndt,学习因子c1、c2,惯性权重wmax和wmin,步长控制因子α,发现概率为pα,搜索上界Ub和搜索下界Lb;


Step7:判断是否满足终止条件,若不满足,转Step4;
Step8:输出粒子最优位置和目标函数最优解,终止算法。
3.3 算法流程
根据基本步骤, 绘制流程图见图3。

图3 R-CS-PSO 算法基本流程图
4 算法性能测试
4.1 使用典型函数测试性能
为了检验所提出的RCS-PSO 算法的性能,我们使用Python 语言进行了编程,使用Sphere 函数、Step 函数、Schwefe1_2.22 函 数、Rosenbrock 函 数、Griewank 函 数、Ackley 函 数、Alpine 函 数 和Rastrigin 函数等[8-9]标准的测试函数, 将R-CS-PSO 算法与PSO 算法、CS 算法进行求解速度、收敛性、鲁棒性等算法性能比较,通过比较发现,改进的算法相比于之前的算法搜索范围广、收敛速度快、能在较短的时间内取得较好的解。
4.2 使用标准背包测试性能
为了进一步检验所提出的R-CS-PSO 算法求解背包问题的性能,我们同样使用Python 语言进行编程,将RCS-PSO 算法与PSO 算法、CS 算法通过经典背包问题进行算法性能测试对比。 选择以下3 个大、中、小背包[10],见表1。

表1 2 个经典的测试背包
为了减少随机性对实验的影响, 每个测试的结果都是程序独立运行20 次的平均值,各背包种群规模等于背包大小,最大迭代次数为500 次。 我们分别通过最优值、最差值、平均值、标准差、成功率和迭代次数等指标来分析。其中成功率为每种算法寻优到理论最优值的成功率,迭代次数为每种算法寻优到单次实验最优值的平均迭代次数。 结果见表2。
分析表2 可以看出, 对于KP-1 背包,R-CS-PSO 算法可以很快找到理论最优解,CS 算法也可以找到理论最优解, 但迭代次数远大于R-CS-PSO 算法的迭代次数,PSO 算法容易陷入局部最优解;对于KP-2、KP-3,随着背包的不断变大,R-CS-PSO 算法可以以一定的成功率找到理论最优解,CS 算法和PSO 算法已不能找到理论最优解,而且从平均值、标准差、迭代次数等也可以看出,RCS-PSO 算法较CS 算法和PSO 算法在解决背包问题中的求解精度、速度和稳定性都更好。

表2 经典测试背包对3 中算法性能测试结果对比
5 结束语
本文在研究粒子群优化(PSO)算法和布谷鸟搜索(CS)算法的基础上,针对两种算法的不同特点,改进的提出了分阶段随机布谷鸟粒子群优化算法(R-CS-PSO),通过选择多个典型函数测试该算法具有较快的计算速度、 较好的收敛性和较强的鲁棒性, 通过标准0-1 背包测试该算法在求解多约束背包问题中具有较好性能, 进而在求解民船装载问题中进行推广应用。

