不同浓度La掺杂LiMPO4（M=Fe，Mn）电子结构及Li+扩散的第一性原理研究

杨晓翠

1997年，PADHI 等［1］首次提出利用橄榄石型LiMPO4（M=Fe，Mn，Co，Ni）作为锂离子电池的正极材料.其中，由于LiMPO4（M=Fe，Mn）具有低成本、高理论比容量、较好循环稳定性和安全性能等优点［2］，受到研究人员的广泛关注.目前，LiFePO4正极材料被大量应用于新能源汽车.LiMnPO4的理论比容量与LiFePO4相同，但电池的工作电压较后者高0.7 V，作为动力电池正极材料有巨大的应用潜力.然而，LiMnPO4的低电子电导率和离子扩散速率阻碍其应用发展［3］，研究通过包覆碳、金属和金属氧化物、减少晶粒的尺寸和在锂位、铁位掺杂金属离子等方法进行改善［4］.在这些方法中，金属离子掺杂作为一种有效的方法备受瞩目.本文利用第一性原理计算对掺杂不同浓度La 的LiFePO4与LiMnPO4进行研究，探索La掺杂对二者电子性质和Li+扩散影响的规律.

1 计算模型和方法

本文采用的模型为橄榄石构型的LiMPO4（M=Fe，Mn），如图1所示，属于正交晶系，空间群为Pnma.模拟计算时，通过对原胞和超胞（121）、（122）中的M 进行置换，得到掺杂样品.晶体结构中P（4c）原子和邻近的4 个O 原子形成PO4四面体，Li（4a）和M（4c）原子同O原子分别形成LiO6和MO6八面体.沿着b轴方向，MO6八面体通过共角的方式相连接，LiO6八面体通过共边的方式连接起来形成链状结构，使得LiMPO4（M=Fe，Mn）沿着b轴存在Li+的一维扩散通道.

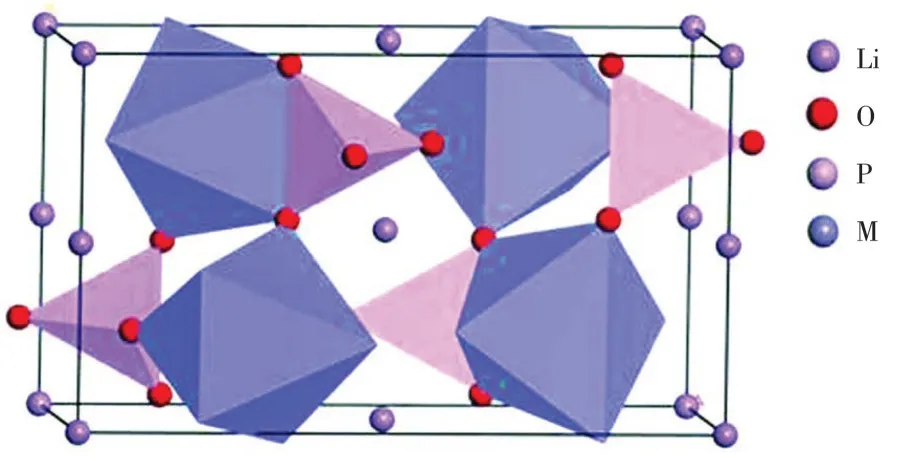
图1 橄榄石型LiMPO4（M=Fe，Mn）的晶胞模型

计算采用Material Studio 8.0 基于密度泛函理论（DFT）的CASTEP 软件包［5］.交换关联函数采用广义梯度近似（GGA）［6］下由PETER 等提出的PW91 交换关联函数.赝势采用超软赝势（ultrasoft），平面波截断能Ecut=380 eV，Brillouin区的积分计算采用3×4×5 的K 网格［7］.原子赝势计算所选取的价电子为Li-1s22s1，O-2s22p4，P-3s23p3，Fe-3d64s2，Mn-3d54s2，La-5s25p65d16s2.几何优化采用BFGS（Broyden-Fletcher-Goldfarb-Shanno）算法，其中最大能量改变的收敛阈值为E/ion=1.0×10-5eV，原子间作用力的收敛阈值为|F|max=0.3 eV/nm，原子位移的收敛阈值为|dR|max=1.0×10-4nm，原子间内应力的收敛阈值为|S|max=5.0×10-2GPa.

2 计算结果与讨论

2.1 掺杂前后晶格参数的变化

LiMPO4（M=Fe，Mn）结构优化后的结果列于表1中.从表1中可以发现，晶胞优化的结果和文献中的计算结果基本一致，比实验值偏大［8］.这主要是由于广义梯度近似中电子的相互作用被低估，使得键长较实验值略长.对比计算值和实验值，晶胞参数a、b和c的变化率均小于1%，在误差范围之内.这也验证了本文所选模型的正确性与计算参数选择的合理性.

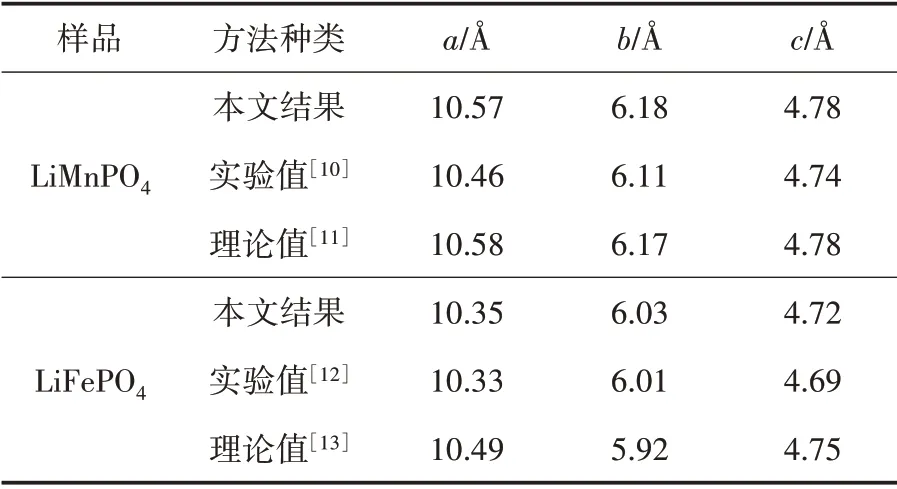
表1 LiMPO4（M=Fe，Mn）结构优化后的晶胞参数与其他结果的比较

图2和图3分别给出了LiFePO4和LiMnPO4La 掺杂前后晶胞参数的变化，晶胞参数的变化是影响Li+扩散速率的重要因素.由于La 的半径大于Fe 和Mn，掺杂必然会引起晶胞膨胀.从图2和图3中可以看出，两种材料掺杂后b、c边长变化很小，晶胞膨胀主要体现在a的伸长.研究表明，Li+的扩散通道是一维的，并且沿着b轴方向［9］.因此a轴的伸长会引起扩散通道的变形，可能会有利于Li+的扩散，但仍具有不确定性，后文将对Li+的扩散进行计算分析.

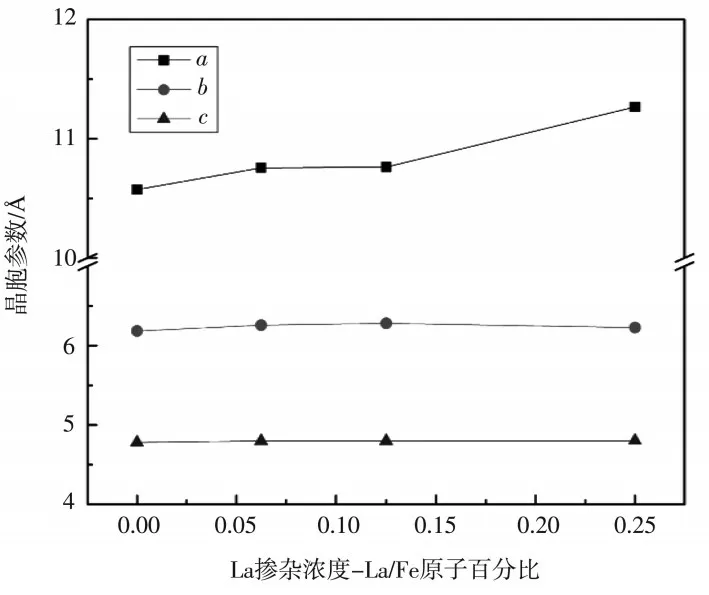
图2 La 掺杂后LiFe1-xLaxPO4 晶胞参数a、b 和c 的变化

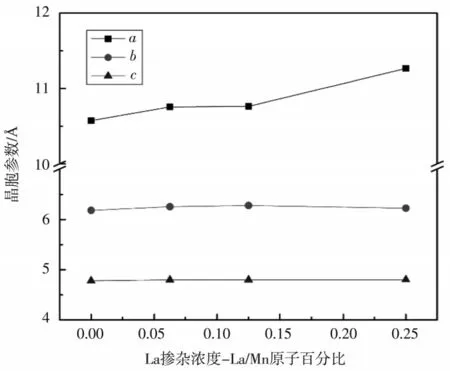
图3 La 掺杂后LiMn1-xLaxPO4 晶胞参数a、b 和c 的变化

2.2 不同浓度La 掺杂的LiMPO4（M=Fe，Mn）的电子结构

表2列出了掺杂前后LiMPO4（M=Fe，Mn）的费米能和带隙数据.其中LiFePO4的带隙为0.21 eV.XU 等［10］计算的结果为0.27 eV，与本文中结果保持一致.从表2可以看出，LiMnPO4的带隙为2.24 eV，ZHOU 等［11］的计算结果为2.0 eV，与本文结果相近.可以看出，LiMnPO4的带隙较大，几乎为绝缘体.

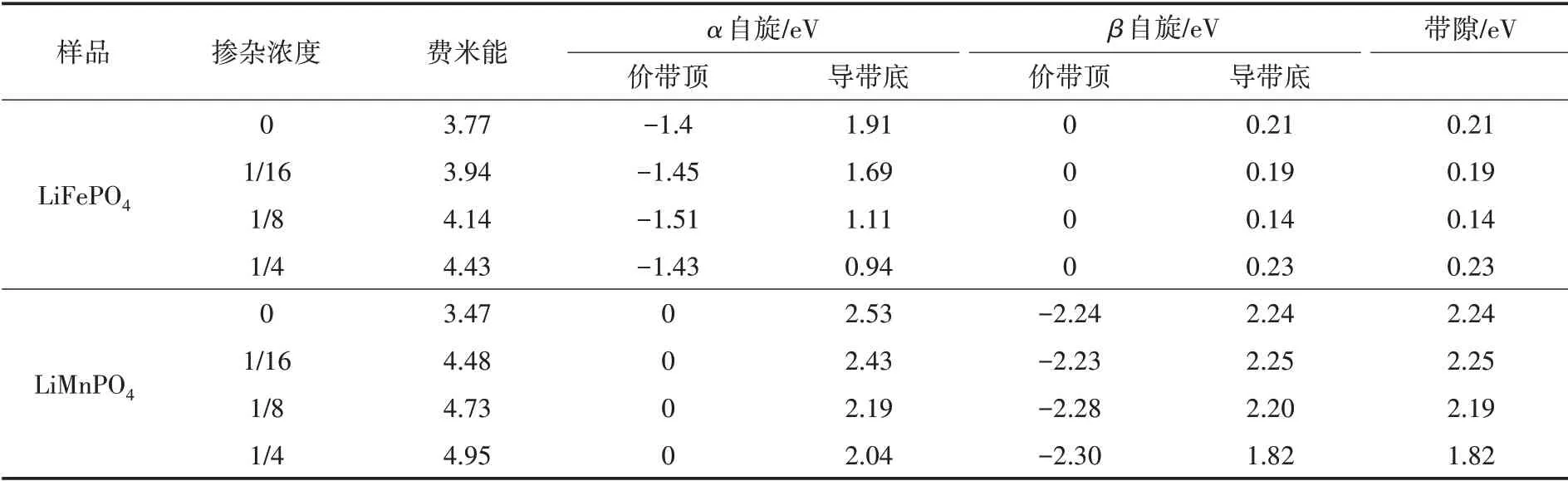
表2 不同浓度La 掺杂LiMPO4（M=Fe，Mn）的带隙及费米能

虽然LiFePO4与LiMnPO4有着一样的对称性和相似的晶格结构，但是由于Fe 原子和Mn原子的价电子数目不同，使LiFePO4与LiMnPO4的电子结构有很大的差异，最终导致二者的电化学性能差异较大.LiFePO4的带隙主要由β自旋的价带顶和导带底决定，随着掺杂浓度的增加带隙先减小后增加.当掺杂浓度为1/8时有最小带隙，最有利于电子的跃迁.LiMnPO4的带隙主要由α自旋的价带顶和β自旋的导带底所决定，伴随着掺杂浓度的增加带隙逐渐减少.当掺杂浓度为1/4 时有最小带隙.二者的费米能都随着掺杂浓度的增加而增加，表明材料充放电电压随着La 掺杂浓度的增加而增大.

图4和图5分别给出了LiFePO4和LiMnPO4掺杂前后费米面附近的态密度.剪刀因子为2 eV.从图4和图5中可以看出，LiMPO4（M=Fe，Mn）中Fe 和Mn 的d 轨道发生明显的分裂.对于LiFePO4而言，其α自旋带隙主要由Fe 的d轨道和La 的d 轨道所决定，β自旋带隙取决于Fe 的d 轨道.对于LiMnPO4而言，其α自旋带隙与LiFePO4相同，主要由Fe 的d 轨道和La 的d轨道所决定，而β自旋带隙是由O 的p 轨道和Mn 的d 轨道所共同决定的.综上所述，LiFePO4的费米面主要由Fe 和La 的3d 轨道所决定，LiMnPO4的费米面主要由Fe 和La 的3d 轨道与O 的2p 轨道共同决定.

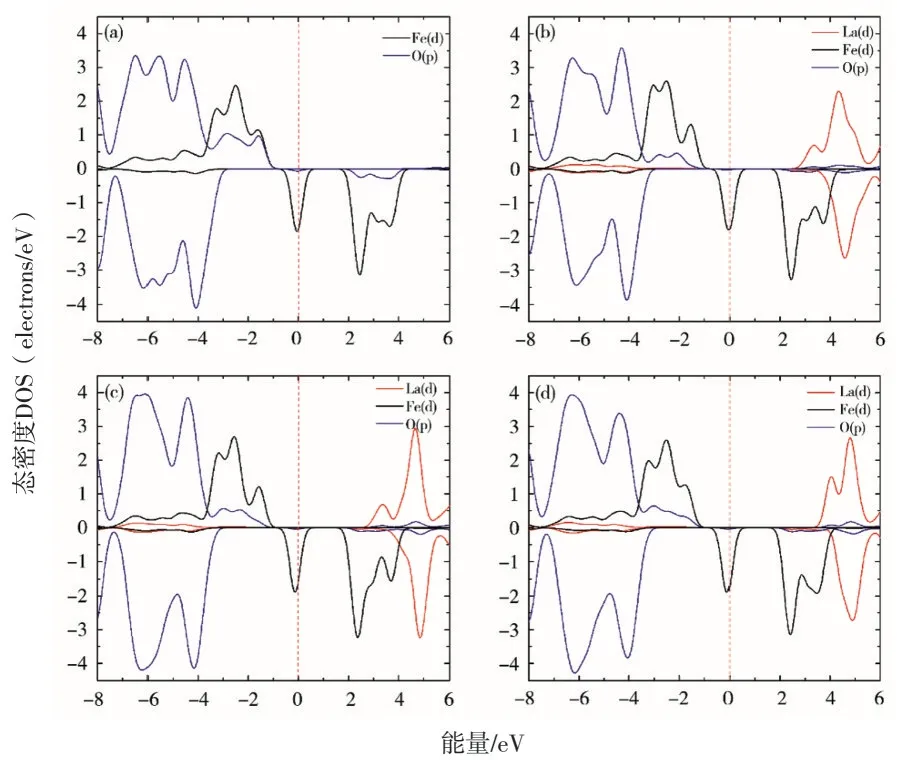
图4 LiFePO4 掺杂前后的态密度图

图5 LiMnPO4 掺杂前后的态密度图

在LiMPO4掺杂体系中La 所形成的峰型相似，都会增加费米面附近的电子浓度，且伴随着掺杂浓度的增加都向费米面方向移动.但在LiMnPO4中La 的初始位置距费米面距离较远，这也是LiMnPO4有着较差导电性的重要原因.此外，La 的加入也使Fe 和Mn 的Eg轨道位置发生移动，这是带隙发生变化的根本原因.同时，从态密度图中也可以发现，在费米面附近Fe、Mn 与O 的轨道分别相互重叠形成共价键，这对于LiMPO4（M=Fe，Mn）在脱嵌Li 的过程中保持结构稳定性也有着一定贡献.

2.3 掺杂前后Li+扩散系数的变化

LiMPO4（M=Fe，Mn）的Li+扩散速率较低，是限制其电化学性能的主要因素之一，因此研究Li+的扩散对橄榄石型LiMPO4（M=Fe，Mn）Li 离子电池的发展有着极其重要的意义.很多研究学者对Li+扩散路径进行了研究，证明了Li+沿Y轴以S 型路径进行扩散［12］.本文将直接通过构造Li 空位对Li+沿Y轴扩散过程进行模拟，利用过渡态搜索计算其迁移扩散势垒.Li+扩散速率可通过以下公式进行计算.

式中：Eα为Li+的扩散势垒，d为Li+扩散所迁移的距离，本计算取d=0.3 nm.ν0代表Li+的晶格振动频率，一般固体中原子的振动频率为1013Hz，本文取ν0=1013Hz，kB为玻尔兹曼常数，T为热力学温标，取T=300 K.计算结果列于表3中.

对于LiFePO4体系而言，从表3中可以看出：①当掺杂浓度为1/16 时有最小扩散势垒0.09 eV，与未掺杂体系相比，扩散势垒明显下降，扩散系数大大增加；②掺杂浓度为1/8 时扩散势垒为0.26 eV，相比未掺杂体系，扩散势垒减小，扩散系数也明显提高；③但当掺杂浓度为1/4 时，由于掺杂浓度过大，可能由于晶格形变严重影响到Li+扩散通道，导致扩散系数降低.因此，La 掺杂明显改变了LiFePO4体系的电化学性能.

表3 掺杂前后各个体系的扩散势垒和扩散系数

对LiMnPO4体系而言，从表3中可以看出：①LiMnPO4体系的扩散势垒为0.39 eV，这与YUSUKE 等［13］通过计算极化子和空穴迁移的方法得到的扩散势垒0.38 eV 是一致的；②La掺杂并未改善LiMnPO4的扩散速率，且随着掺杂浓度的增加其扩散系数变小，这是因为晶格产生扭曲变形所导致的，并且这种形变对LiMnPO4扩散系数的影响要大于对LiFePO4的影响.

3 结论

本文采用第一性原理对不同浓度La 掺杂的LiMPO4（M=Fe，Mn）的晶胞结构、电子结构和Li+扩散速率进行了系统研究.研究结果表明：①二者晶胞参数与实验参数吻合较好，表明计算的稳定性和参数选择的合理性.随着La 掺杂浓度的增加，只有a变长，其余晶格常数基本保持不变.②LiMPO4（M=Fe，Mn）虽然有着相似的结构和对称性，但是带隙分别为0.21 eV 和2.24 eV，导电性能差异较大.③当La掺杂浓度为1/8 和1/4 时，LiFePO4与LiMnPO4分别具有最小带隙.④LiFePO4在掺杂浓度为1/16时有最大扩散系数，但La 掺杂并不能有效改善LiMnPO4的扩散速率，二者伴随La 掺杂浓度的增加都会降低Li 离子的扩散速率.