基于多通道长短期记忆网络的PM 2.5小时浓度预报

张鑫磊，张冬峰*，刘 伟，杨 倩，郭媛媛，任玉欢，范志宣

1.山西省气候中心，山西太原 030006

2.吉林省气象科学研究所，吉林长春 130062

PM2.5指空气动力学直径小于等于2.5μm的细颗粒物，是近年来主要的大气污染物之一.研究[1-3]表明，在高浓度PM2.5环境下暴露数小时后，将增加患心血管疾病和呼吸道疾病的风险.因此，对未来多小时的PM2.5浓度进行逐小时滚动预报，可以提醒相关疾病易感人群及时调整出行计划、提早预防短期高浓度PM2.5引发的健康问题，并进一步推动政府制定紧急预案，完善大气污染治理制度[4].

目前关于PM2.5浓度预报的方法主要可分为两大类.第一类是基于气象学与数学理论的数值模拟方法，通过对污染物传输、扩散、转化以及沉降等过程进行模拟，对污染物浓度进行预报[5].比较有代表性的几个污染物模式为美国环境保护局研发的第三代空气质量预报与评估系统中的CMAQ(Community Multiscale Air Quality)模式[6-7]、美国国家气候中心预报系统实验室开发的气象-化学耦合模式WRF-Chem[8]以及由中国科学院大气物理研究所研发的嵌套网格空气质量预报模式系统NAQPMS[9]等.第二类是基于对历史资料进行分析的统计方法与机器学习(深度学习)方法，通过对历史数据的学习与分析，挖掘数据内在特征，基于当前的状态对未来给出较合理的预报.相较数值模拟方法来说，第二类方法更为简单、高效，且适用性广[10].其中，有基于统计方法的多元线性回归[11]、非线性回归[12]等模型，基于机器学习方法的极端梯度提升(Extreme Gradient Boosting, XGBoost)[13]、随机森林(Random Forest, RF)[14]与极限学习机(Extreme Learning Machine,ELM)[15]等模型，基于深度学习方法的卷积神经网络(Convolutional Neural Networks,CNN)[16-17]与循环神经网络(Recurrent Neural Network,RNN)[18-20]等模型.

随着计算机芯片的发展，图形处理器(Graphics Processing Unit,GPU)被应用到深度学习模型训练中.作为机器学习方法中的一个新领域，深度学习不仅在序列预测与特征提取等方面优于传统的机器学习方法，而且在数据预处理上也节省了较多的时间.在模型输入要素的选取上，以空气质量监测站各类污染物浓度为基础，多位学者先后融合了监测站周围的气象条件、时间信息以及地理信息，有效提升了模型的预报精度[21-24].在观测窗与预报时效的选择上，多数研究利用8~72 h历史资料来预报未来1~24 h的逐小时PM2.5浓度[24-27].但这些研究中观测窗的宽度多为人为选取的固定值，可能无法获取最优的预报结果.选取合理的观测窗宽度，一方面可提升模型预报的准确性，另一方面也可以减少观测窗过宽导致的运算成本[25-26]. 在预报模型构建上，有学者提出了CNN-RNN[24]、长短期记忆网络(Long Short-Term Memory,LSTM)[25]以及CNN-LSTM[26]等深度学习预报模型，这些模型通过提取站点所有要素的历史时间序列信息，对站点未来逐小时PM2.5浓度进行预报.在此基础上，也有学者利用三维卷积神经网络(3D-CNN)[21]、卷积长短期记忆网络(Convolutional LSTM,ConvLSTM)[23]和图卷积神经网络(Graph Convolutional Network, GCN)[27]等模型进一步提取了输入要素的空间特征，获得了较高的预报精度，但同时也增加了数据预处理的难度以及模型的复杂度.

综上，已有研究多为单个模型提取所有要素的时间序列及空间信息，然而不同要素的有效信息可能存在差异，对所有要素使用同一个神经网络进行处理，或许无法获取较高的预报精度；同时，以往研究中仅选取固定宽度的观测窗也会对预报精度产生一定影响.因此，为进一步提升预报精度，该研究以太原市为研究区域，提出了一种多通道长短期记忆网络(Multi-Channels Long Short Term Memory，MULTI-LSTM)模型，使用独立的LSTM模型分别提取不同要素的历史时间序列信息，利用不同气象站点融合得到的气象数据作为辅助输入要素，对不同观测窗与预报时效组合下模型的预报精度进行评价，以期为PM2.5预报研究中输入要素、观测窗选取和模型构建等问题提供新的研究思路.

1 材料与方法

1.1 研究区域概况与数据预处理

太原市位于山西省中部，位于37.45°N~38.42°N、111.5°E~113.15°E之间.总面积6 988 km2，截至2021年底常住人口为539万.该文选取了太原市2019−2020年的空气污染物与气象要素小时资料.空气污染物观测数据源于中国环境监测总站的全国城市空气质量实时发布平台(https://air.cnemc.cn:18007)，污染物包括PM2.5、PM10、NO2、CO、O3和SO2共6种.气象要素观测资料来自于太原市国家气象观测站与区域气象观测站(分别简称“国家站”与“区域站”).

该文选取的气象资料包括距离每个空气质量监测站最近的国家站的小时相对湿度、露点温度、2 min平均风向/风速、10 min平均风向/风速、地面温度、1 min/10 min能见度，以及每个空气质量监测站5 km范围内所有区域站的小时气温与降水要素的平均值.对个别缺失数据进行插补，将空气质量数据与气象数据按站点与时间合并，并将站点当前季节、月份以及小时等时间要素作为扩展属性添加到资料中.最终共获得20个要素，140 056条有效观测数据.空气污染物和气象资料的数值类要素统计结果如表1所示.

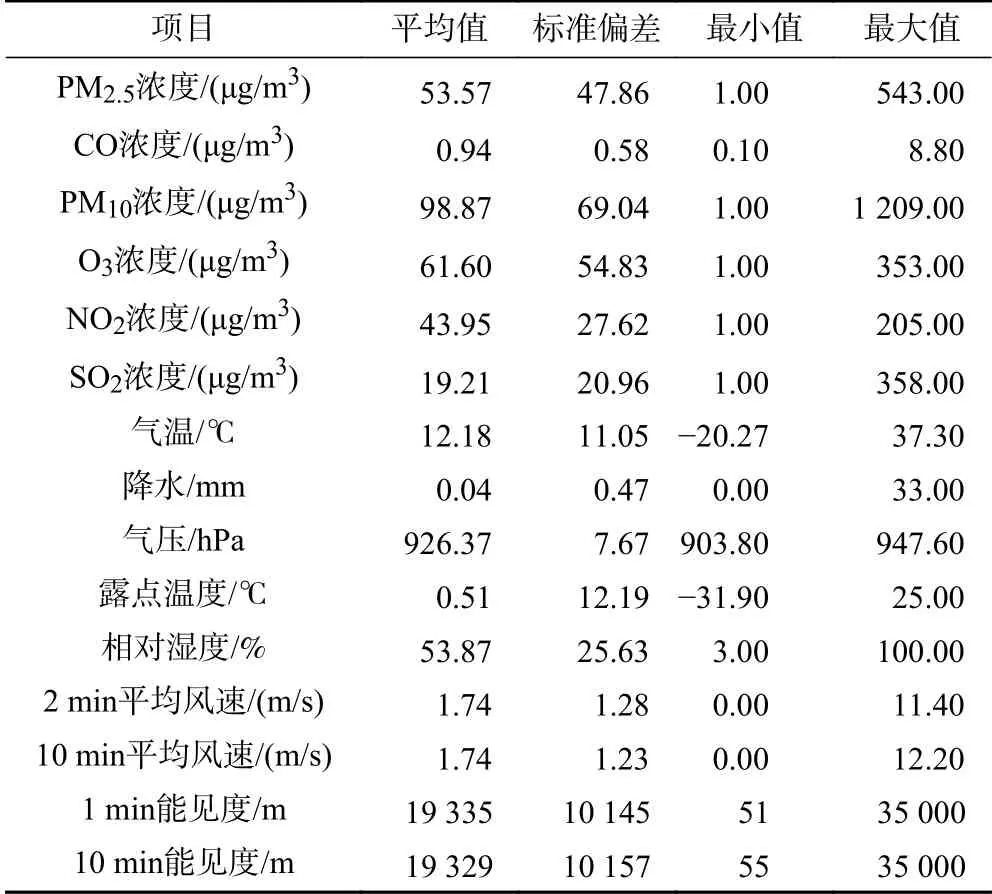
表1 空气污染物和气象资料的数值类要素统计结果Table 1 Statistical analysisof numerical elements of air pollutants and meteorological data

对空气污染物和气象数据的数值类要素进行归一化处理，对风向、季节等非数值类要素进行独热编码处理.从每个站点数据中选取80%样本组成训练集，剩下的20%组成测试集.另外，在训练集中抽取5%的样本作为模型训练时的验证集，用于超参数的调整，以期获得预报精度较高的模型.

1.2 预报模型构建

由图1可见，该文基于LSTM神经网络进行深度学习模型构建，LSTM通过遗忘门Ft、输入门It与输出门Ot在单元之间传递信息，从而控制上一时刻信息与当前时刻信息的记忆与遗忘的程度.作为RNN的一种，LSTM可以弥补传统RNN在长期记忆上导致的梯度爆炸或梯度消失的缺陷.遗忘门Ft与输入门It控制着细胞状态Ct，通过对上一时刻隐藏层状态Ht−1以及当前时刻输入信息Xt的输入与遗忘，对细胞状态Ct进行更新.输出门Ot则控制隐藏层状态Ht，通过输出门Ot以及细胞状态Ct来更新当前时刻的隐藏层状态Ht，LSTM神经网络通过历史序列信息的输入，不断更新细胞的隐藏层状态Ht，以达到提取特征序列(时间)信息的目的[28].

图1 LSTM细胞结构Fig.1 Cell structure of LSTM

图1中LSTM输入输出过程如式(1)~(8)所示.

式中：σ与tanh分别表示sigmoid函数与双曲正切函数；Wf、Wi、Wc、Wo、bf、bi、bc、bo均为模型参数，通过迭代训练不断更新.

构建MULTI-LSTM模型有以下几步：首先，利用LSTM较强的时序处理能力，分别对每个要素的历史时间序列样本(过去逐n小时历史资料)进行处理；然后，将各要素的处理结果通过Merge层进行融合；最终，通过3层全连接神经网络输出未来逐m小时的PM2.5浓度.MULTI-LSTM模型结构见图2.为防止过拟合，使用Dropout层随机移除一定比例的神经元以降低神经元之间的复杂性[29]，优化函数采用Adamax[30].

图2 MULTI-LSTM模型结构Fig.2 The structure of MULTI-LSTM model

为了对比模型预报精度，分别构建单通道LSTM模型(BASE-LSTM)和LSTM扩展模型(LSTM extended,LSTME)[25].利用各模型对多组观测窗-预报时效的数据集进行学习，核心参数如表2所示.

表2 训练参数Table2 The training parameters

该试验基于Python 3.8.5软件，利用谷歌深度学习开源框架Tensorflow-gpu 2.4.1以及GPU并行计算构架cuda 11.0，构建并训练上述模型.CPU为Xeon Gold 5222@3.80 GHz四核，使用1块Nvidia Quadro P2000(5 GB)的显卡进行GPU运算.

1.3 评价指标

为了更好地评估模型的准确性，在测试集上对模型的预报值与观测值进行对比，从而评价预报效果.该研究采用均方根误差(RMSE)、平均绝对百分误差(MAPE)以及拟合指数(IA)作为评价指标.通过RMSE可以反映预报结果整体的精确度，评估整体的绝对误差.MAPE用于相对误差的测量，评估不同等级污染过程误差的百分比.IA则用于比较预报值与观测值的分布相似度，IA越接近1，说明二者越一致[24].

2 结果与分析

2.1 预报精度对比

以8 h观测窗与6 h预报时效的MULTI-LSTM模型为例，模型训练过程的损失函数如图3所示.BASE-LSTM模型、LSTME模型和MULTI-LSTM模型在8 h观测窗与不同预报时效组合下的RMSE如图4所示.由图4可见，MULTI-LSTM模型在不同预报时效下均表现最佳，在对观测窗为8 h、预报时效为1 h(以下简写为“观测窗/预报时效”的形式，此处为“8/1”)的预报中，RMSE为10.67μg/m3，IA在0.98以上，与BASE-LSTM模型表现相近，优于LSTME模型.但随着预报时效延长，BASE-LSTM模型的预报精度明显下降，MULTI-LSTM模型逐渐优于其他两个模型.与BASE-LSTM模型和LSTME模型相比，在“8/6”组合下MULTI-LSTM模型的RMSE分别降低了7%和6%.

图3 MULTI-LSTM模型训练过程损失函数图Fig.3 Loss function of the training process of MULTI-LSTM

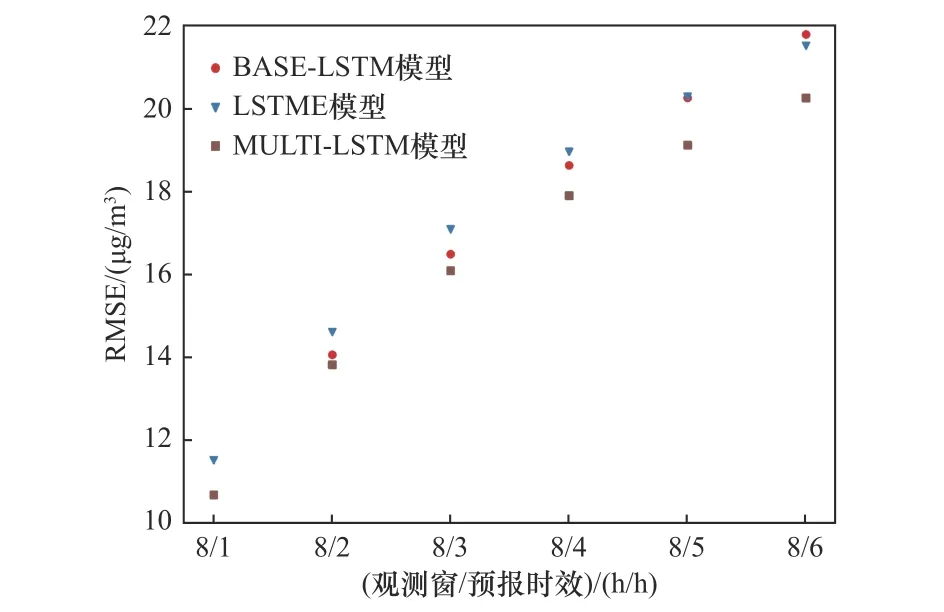
图4 8 h观测窗下不同预报时效的RMSEFig.4 The RMSE of different period validities in 8 hoursobservation windows

在6 h预报时效与不同观测窗宽度的组合下，MULTI-LSTM模型的预报精度最高(见图5).MULTILSTM模型在8~32 h的观测窗内RMSE基本没有变化，在40~48 h观测窗内略有减小，相比较于8 h观测窗，观测窗宽度为40和48 h的RMSE分别降低了2%与3%.BASE-LSTM模型与LSTME模型的预报精度基本一致，在观测窗宽度小于等于40 h范围内，随着观测窗的变宽，LSTME模型的RMSE基本没有变化，而BASE-LSTM模型的RMSE略微减小.当观测窗宽度为48 h，BASE-LSTM模型与LSTME模型的RMSE均略有减小.

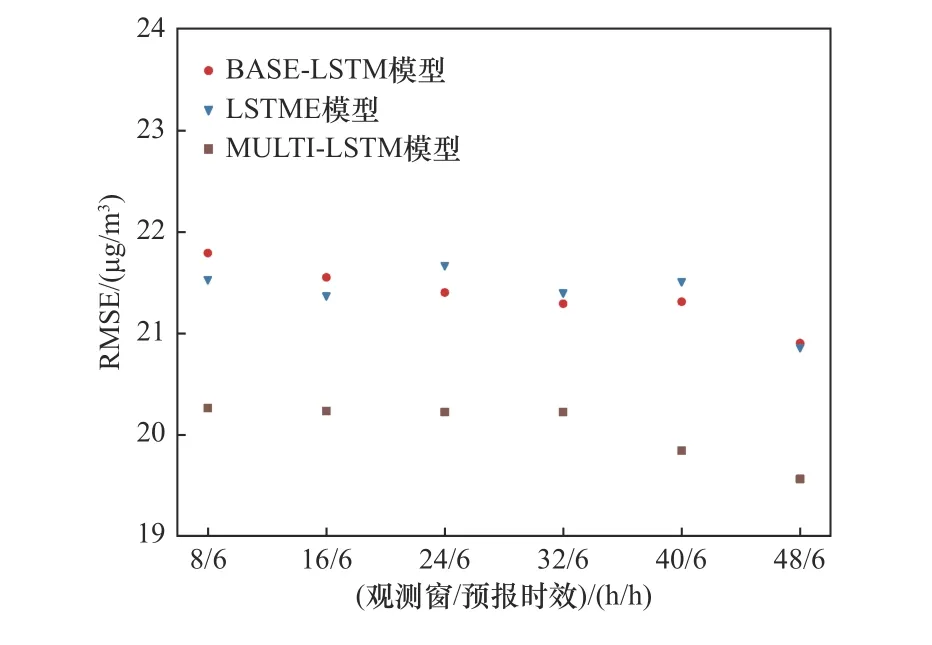
图5 不同观测窗下6 h预报时效的RMSEFig.5 The RMSE of different observation windows in 6 hours period validities

对原始数据集进行相关性分析，分别计算原始数据过去第n小时各输入要素值与未来第m小时PM2.5浓度之间的相关系数.对过去第n小时各输入要素值与未来第m小时PM2.5浓度之间的所有相关系数取绝对值后求平均值，得到平均相关系数(见图6).由图6可见，6条曲线的变化趋势一致.曲线的变化主要分为4个阶段，以未来第1小时PM2.5浓度与各输入要素值的平均相关系数曲线为例，前15 h为下降阶段，平均相关系数由0.35降至0.24；第16~24小时趋于平稳，平均相关系数在0.23~0.24之间；第2个下降阶段为第25~39小时，平均相关系数由0.23降至0.17；第40~48小时平均相关系数略有升高，由0.17升至0.18.故根据预报结果与相关性结果可以推断，增加输入历史序列的长度对预报精度提升的影响相对较小，只需根据相关性分析选取合适的输入历史序列长度.该文中进一步提升预报精度的观测窗宽度为40~48 h.

图6 过去第n小时各输入要素与未来第m小时PM 2.5浓度的平均相关系数Fig.6 Average correlation coefficient between inputs for the past n-th hour and PM 2.5 concentration for thenext m-th hour

2.2 预报性能评价

分别统计了不同PM2.5污染等级下3个模型在“8/6”组合下测试集的预报情况[31]，并将MAPE作为评价指标(见表3).由表3可见，MULTI-LSTM模型的MAPE最小.

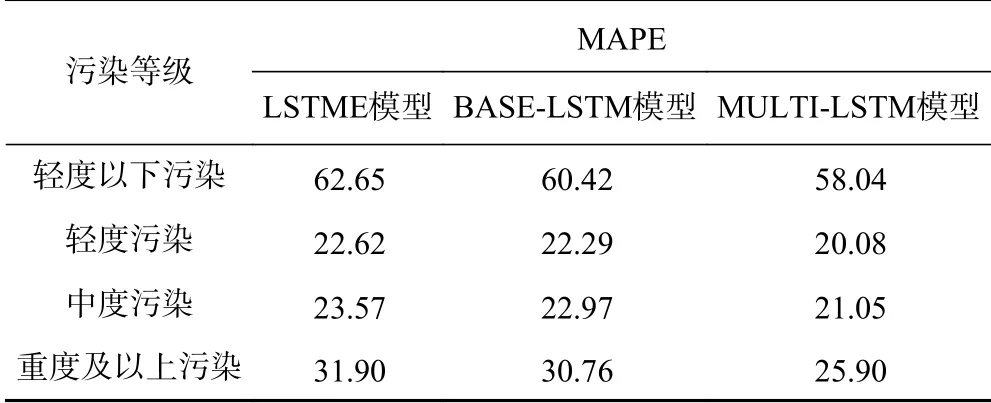
表3 不同模型在不同PM 2.5污染等级下的预报效果(MAPE)Table 3 MAPE of different models in different PM 2.5 pollution process class

对上兰站(监测站编号：1083A)测试集时段的预报值与观测值进行对比，选取了3个模型在“8/6”组合下未来6 h预报值与观测值的平均值(见图7).由图7可见，BASE-LSTM模型、LSTME模型与MULTILSTM模型的预报值与观测值之间的R2分别为0.94、0.93和0.97，MULTI-LSTM模型预报值与观测值的一致性优于其他模型.此外，根据散点密度图的线性拟合可以发现，3个基于LSTM构建的深度学习预报模型均存在一定程度的PM2.5低浓度预测偏高以及高浓度预测偏低的问题，但根据预报序列与观测序列的重合程度来看，对于高浓度PM2.5的预测，MULTI-LSTM模型的预报值与观测值重合程度更高.

图7 上兰站PM 2.5观测值与不同模型预报值的对比Fig.7 Comparison of PM 2.5 observation values and prediction values of different models in Shanglan station

2.3 网络深度测试

对“8/6”组合下不同LSTM层数的MULTI-LSTM模型进行训练，模型预报精度如表4所示.由表4可见，将LSTM层数从1层增至7层，RMSE略有升高，而MAPE与IA变化均不明显，故增加网络层数无法明显提升网络的预报精度.

表4 不同LSTM层数的MULTI-LSTM模型整体预报精度Table 4 Accuracy of different LSTM layersof MULTI-LSTM model

3 讨论

通过对比不同观测窗与预报时效下各模型的预报精度发现，BASE-LSTM与LSTME模型预报精度相当，但均低于MULTI-LSTM模型. 利用独立的LSTM对每个要素进行训练，明显提高了模型对PM2.5浓度的预报能力.同时，对于基于LSTM构建的深度学习预报模型来说，输入要素历史序列的有效信息具有一定长度，选择合适的观测窗宽度可以减少模型训练的时间成本.以MULTI-LSTM模型为例，选择8 h与32 h历史要素预报未来逐6 h的PM2.5浓度，预报精度基本相同(RMSE分别为20.26、20.22μg/m3)，将观测窗宽度增至40 h，预报精度才会进一步提升(RMSE为19.84μg/m3).

选择合适的网络层深度也可以减少模型训练的时间成本，从网络深度测试的结果来看，增加网络深度并没有进一步提升预报精度.当LSTM层数为7时，MULTI-LSTM模型1个训练周期(epoch)用时为37.5 s，与LSTM层数为1的1个epoch用时(5.6 s)相比，增加了约6倍.

对于气象数据的选取，与不使用气象要素或使用单一来源的气象要素相比，该文使用了不同观测级别气象站的气象数据作为研究区域内空气质量监测站对应的气象要素.其中，区域站在地理分布上更密集，从而为周围空气质量监测站的PM2.5预报提供更多有效预报信息.国家站观测要素的种类更为丰富，可进一步挑选与PM2.5浓度变化相关的要素，为模型训练提供更多相关信息.在后续研究中，可考虑加入气象再分析数据，将不同位势高度的气象要素输入到模型中，以期进一步提高模型的预报精度.

与CNN-LSTM[26]、GCN-Attention-Seq2Seq[27]、STAM-STGCN[32]、ST-LSTM[33]等基于深度学习的PM2.5浓度逐小时预报模型相比，该文提出的MULTI-LSTM模型将多个要素分别输入到不同的LSTM模型中，分别提取不同要素的信息，从而降低了模型的复杂性，同时也获得了相对较高的预报精度(见表5).模型复杂性降低，一方面可减少模型训练的时间与数据预处理的难度；另一方面，也能进一步避免模型过拟合现象的发生.

表5 不同模型预报精度对比Table 5 Prediction accuracy of each model

4 结论

a)该研究利用2019−2020年太原市空气质量监测站、国家气象观测站和区域气象观测站逐小时数据，提出一种MULTI-LSTM模型，其使用独立的LSTM分别对各要素进行处理，解决了不同要素的历史时间序列对PM2.5浓度预报结果响应情况存在差异的问题.

b)对BASE-LSTM、LSTME和MULTI-LSTM模型进行比较，结果表明，MULTI-LSTM模型在不同观测窗与预报时效组合下的RMSE均低于其他2个模型；同时，在一定范围内增加观测窗宽度或提升网络深度无法进一步提升模型的预报精度.

c)通过选择合适的观测窗宽度和气象要素，以MULTI-LSTM模型作为太原市短期PM2.5浓度预报模型，可获得精度较高的预报结果，在8 h观测窗和6 h预报时效组合下，RMSE、MAPE和IA分别为20.26 μg/m3、51%和0.91.下一步将利用MULTI-LSTM模型开展其他污染物的短期预报研究，以进一步验证模型的预报性能和泛化能力.