基于MLP的磁导航机器人方向控制系统设计

孙 鑫，曲立国，陈国豪，陈晴晴

(安徽师范大学 物理与电子信息学院，安徽 芜湖 241000)

0 引 言

智能机器人是一个集环境感知、信息处理、速度与转向控制等功能于一体的综合系统，具有道路障碍自动识别、自动控制以及路径识别等功能[1]. 目前，磁导航是工业自动化系统中一种重要的导航方式，为适应工位布置需求，工业现场除了直道和弯道常规路径元素之外，还存在十字、X型以及环岛等特殊路径元素，这极大地增加了路径识别难度. 此外，磁导航机器人舵机控制系统是一类强耦合性、时变的非线性复杂系统，生产运输过程中容易受环境温度、现场噪声、磁感应传感器互感等因素的干扰，导致磁导航偏离设定路径，复杂路径识别率偏低等问题[2].

为了解决上述问题，控制系统一般采用分段式PID控制算法来实现对小车在直行、转弯和停车三种状态下存在的位置偏差和角度偏差的控制[3-4]. 文献[5]中采用自适应模糊神经网络的机器人路径规划方法对复杂路径进行判断. 文献[6]中提出一种磁场诱导的导航方法，其中，移动机器人在电磁场Fb影响下的行为模仿了带电粒子在载流导线附近移动的行为. 神经网络模型大部分是在PC端实现，应用于MCU嵌入式系统的还比较少[7-9]. 本文构建基于多层感知机(Multilayer Perceptron，MLP)神经网络的路径识别轻量化模型，并基于英飞凌单片机来实现模型部署，最终完成了基于MLP的磁导航机器人方向控制系统设计. 通过对比MLP神经网络的输出结果和传统PID[10]控制的结果，验证了MLP轻量级神经网络在磁导航路径识别方面的优良性能.

1 系统设计

磁导航机器人控制系统以英飞凌TC264单片机作为主控芯片，结合传感器模块、执行机构模块和辅助结构模块等基本外设构成硬件系统[11]，如图1 所示. 首先，系统利用较短前瞻电感传感器为模型提供训练数据，利用较长前瞻电感传感器进行路径识别，将训练数据输入MLP神经网络模型中进行预训练. 然后将模型部署到MCU上，并移除长前瞻电感传感器，神经网络利用短前瞻电感输入的实时数据预测输出PWM值，通过MCU作用于舵机控制电路. 在磁导航机器人控制系统中部署MLP轻量化模型可以提高路径识别的准确率[12].

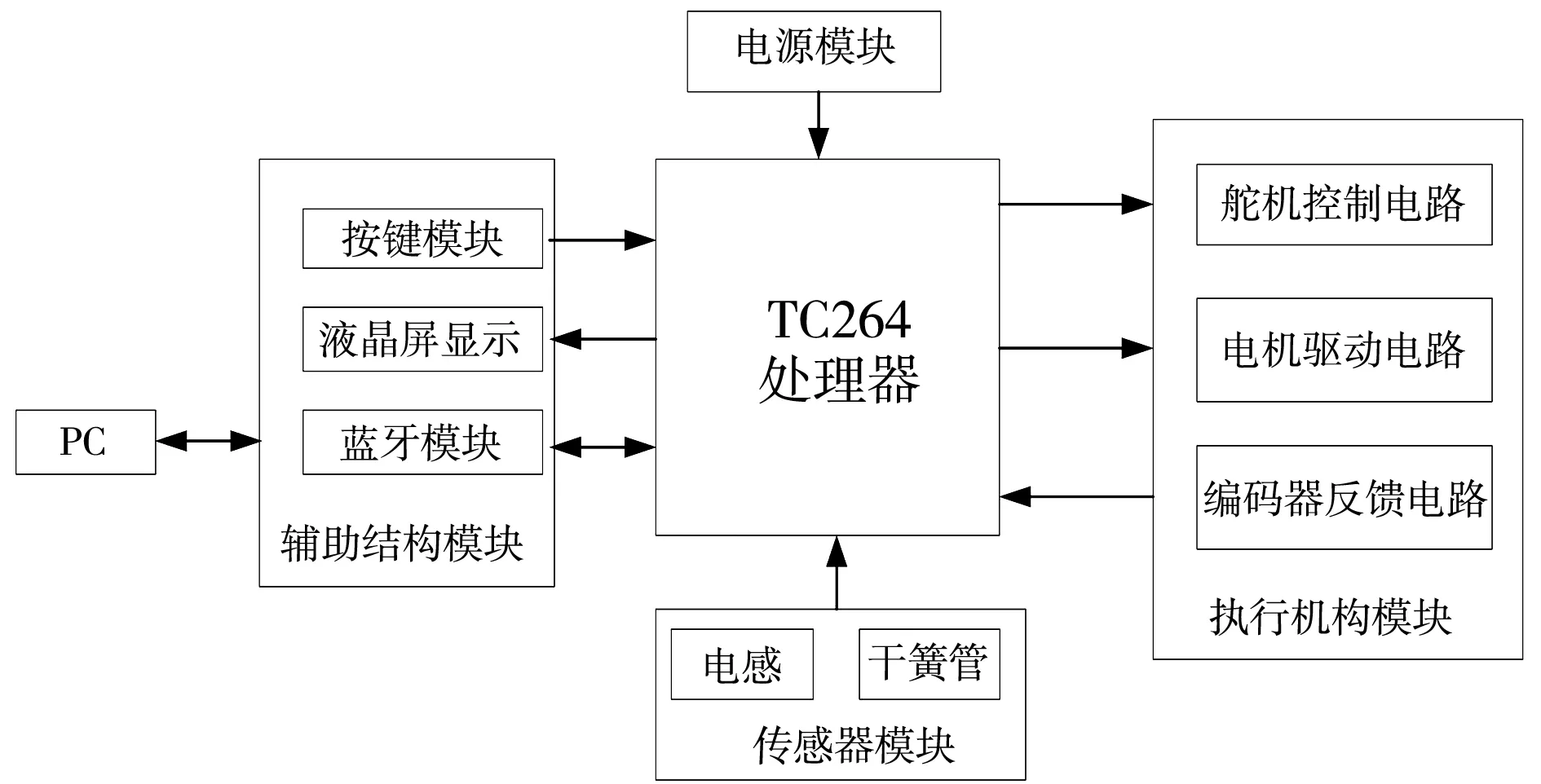
图1 系统整体架构Fig.1 Overall system architecture

执行机构模块包含舵机控制电路、电机驱动电路和编码器反馈电路. 舵机控制电路如图2 所示，该电路为舵机提供4 V～6 V可调电源电压，并将MCU的PWM信号传输给舵机，从而实现MCU对舵机的闭环控制. 电机驱动电路采用2片IR2104半桥芯片组成全桥驱动电路，控制电机可以正反转. 编码器反馈电路通过正交解码获得电机当前转速，实现PID闭环控制.

图2 舵机控制电路Fig.2 Control circuit of steering gear

磁导航方向控制系统需要将采集模块采集到的信号作为MLP神经网络的输入. 采集模块通过电感传感器采集磁场信号后进行信号放大，由A/D转换器进行采样，利用主控芯片进行滤波等处理后，输出满足系统控制要求的信号. 采集模块采用OPA2350运放芯片，其最大放大倍数为1 500倍. 信号放大电路如图3 所示，该电路的放大倍数可以根据磁场强度来改变电阻进行调整，最大放大倍数可达 201倍.

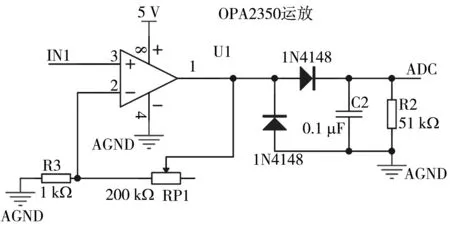
图3 信号放大电路Fig.3 Signal amplification circuit

2 路径识别复杂性分析

路径识别是磁导航技术的关键技术，由于在一根磁导引线的周围会存在多条磁导引线磁场，根据电磁感应原理，该磁导引线上产生的电磁信号会被非线性地累加，此时电感采集的信号与真实值之间存在一定误差，这将增加复杂路径识别的难度，导致导航准确率的下降.

本文系统的导航线选用直径约为0.5 mm的漆包线，输入频率为20 kHz、强度为100 mA的交变方波电流，就会产生导航磁场. 根据Biot-Savart定律可知：通有稳恒电流I、长度为L的直导线在距导线r处的磁感应强度为

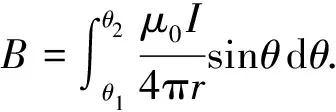
(1)

将式(1)应用于无限长直流电流，积分可得

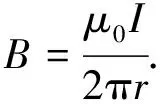
(2)

若在图4 点P处放置一电感线圈，当导线周围磁场随导线中电流按一定规律变化时，根据法拉第电磁感应定律得到电感线圈的感应电动势为

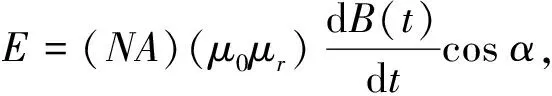
(3)

式中：N为线圈匝数；A为线圈横截面面积；α为磁场方向与线圈轴线的夹角.

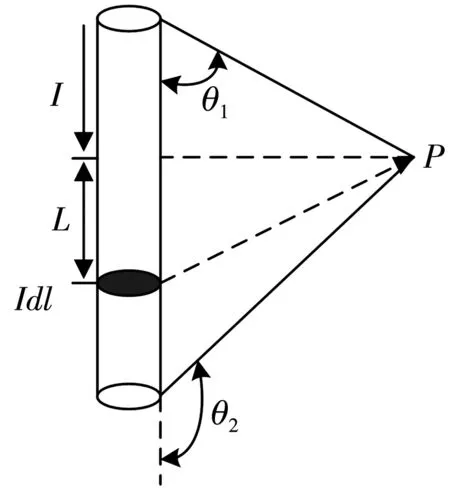
图4 直流电流磁场计算示意图Fig.4 Schematic diagram of DC current magnetic field calculation

结合系统所用的交变电流和电感线圈的特点，将导线周围小范围内的磁场近似为匀强磁场来分析. 线圈中的感应电动势为

(4)

由式(4)可知：线圈的感应电动势与引导线的电流变化率成正比，与线圈中心到引导线的距离成反比.

在机器人路径选择过程中，路径选取具有较强的随机性，路径的状态信息可以有多种不同的表达方式. 在传统PID控制方式下，路径识别的准确率较低，主要有以下两方面的原因：

1) 电感之间的相互影响会对复杂路径的识别产生干扰. 电感之间存在互感现象，采集的信号十分不稳定. 式(5)反映了两个电感传感器之间的相互影响.

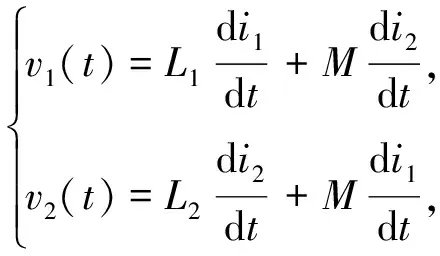
(5)

式中：V1，V2为两个电感传感器两端的电压；L1，L2为两个电感传感器的自感；M为两个电感之间的互感.

由图5 可知，当单个电感采集时，电感值大小的波动幅度较小，当多个电感同时采集时，相同位置电感值波动的时间范围与单个电感单独作用时的相同，但电感值大小的波动幅度要比单个电感单独作用时大得多.

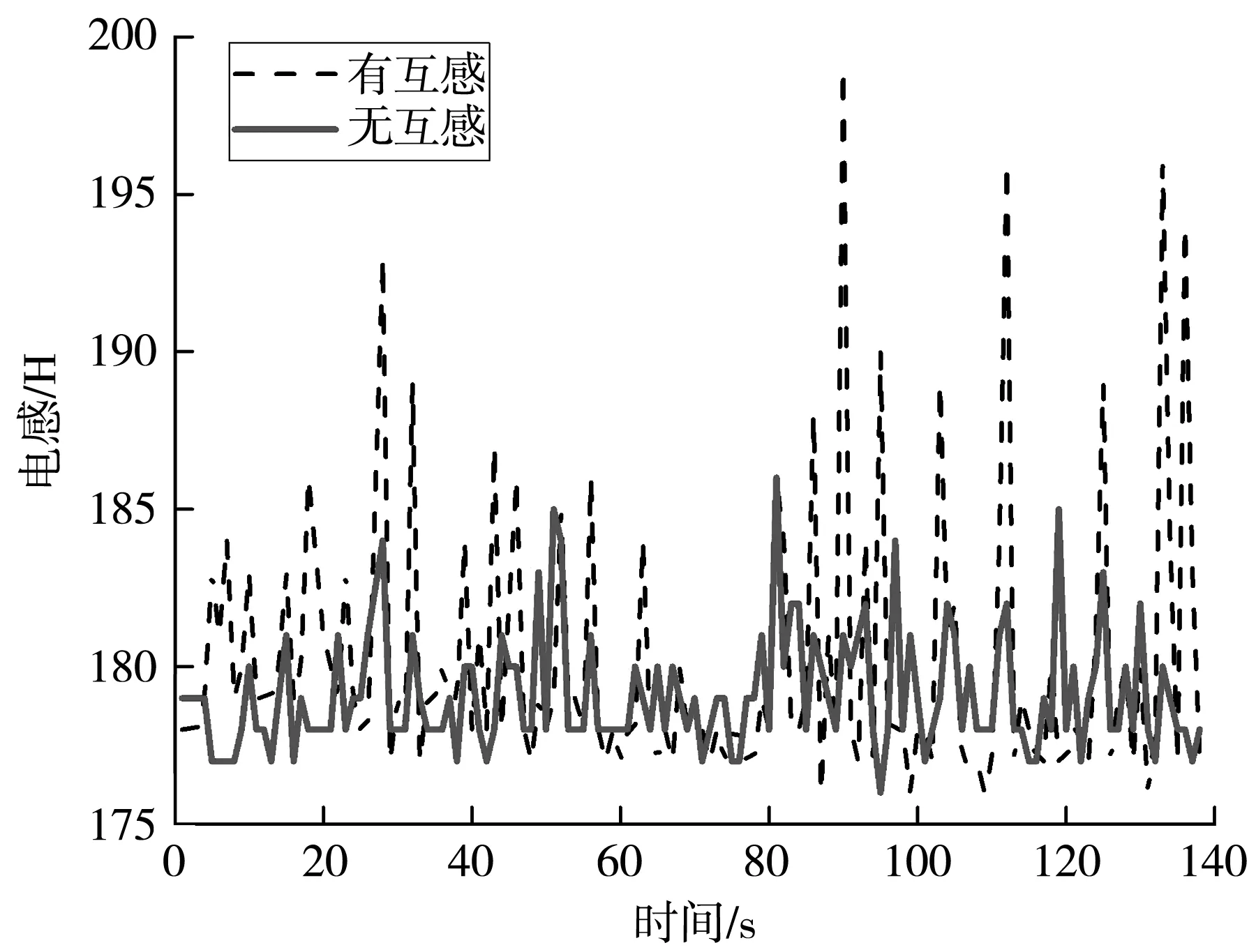
图5 互感对电感的影响Fig.5 Influence of mutual inductance on inductance

2) 在一些路径的交叉点和一些特殊位置，由于周围磁感线的空间分布，系统采集值是空间磁场耦合作用的结果，使用传统PID控制，无法满足磁导航方向控制系统稳定性和准确性的要求.

利用传统PID控制机器人舵机转向，可实现简单道路元素的路径规划. 但是，当工业现场路径比较复杂，外界干扰比较剧烈时，传统PID控制方法对路径信息的描述过于单一，很难将路径信息与目标进行准确对应，导致复杂路径下机器人的路径规划不合理，路径识别的正确率无法保证.

3 MLP神经网络模型

3.1 模型概述

MLP神经网络是一种前馈人工神经网络模型，可以将一组输入向量映射到一组输出向量. 本文改进的MLP模型框架如图6 所示，它是一种五层前馈网络，包括一层输入层、三层隐藏层和一层输出层.

图6 MLP神经网络基本结构Fig.6 Basic structure of MLP neural network

模型输入层接收7路电感传感器的输出信号作为其输入数据，通过全连接层送入三层隐藏层中进行计算，最终输出层输出控制舵机的PWM值.

改进后的神经网络模型中，三层隐藏层中的神经元个数分别为140，100，40. 为了降低模型的计算量并防止模型过拟合，在隐藏层中添加dropout层来进行正则化，dropout层中丢弃率为0.5.

本文的改进模型还进行了数据的归一化处理，使数据集服从均值为0，方差为1的正态分布. 这样不仅使数据分布一致，而且能够能够避免出现神经网络梯度消失的问题. 为了获得更好的性能，在隐藏层之间采用tanh函数作为激活函数，tanh函数在特征相差明显时的效果很好，在循环过程中会不断扩大特征效果. tanh函数表达式为

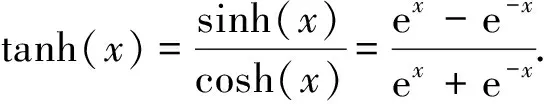
(6)

3.2 数据的采集与处理

为了保证所获取数据的准确性和可靠性，在传输协议的设计中，设定每传输一帧数据就在数据结尾添加一个校验字节，如表1 所示，其中字节1,2组合是时间，字节2到9是电感1到7的采集值，字节10是舵机的PWM值，字节11是校验位. 为了方便数据传输，使用蓝牙透传的方式.

将数据传输到PC端后，在PC端用串口调试助手对数据进行接收，并将数据保存为.txt文件. 然后使用随机采样的方式分割数据集，将数据分为训练集、测试集和验证集，其中80%为训练集，10%为测试集, 10%为验证集.

解决通信协议后，采用的数据获取方式不同，MLP神经网络识别的准确性率也会所不同，下面分析两种数据获取方式.

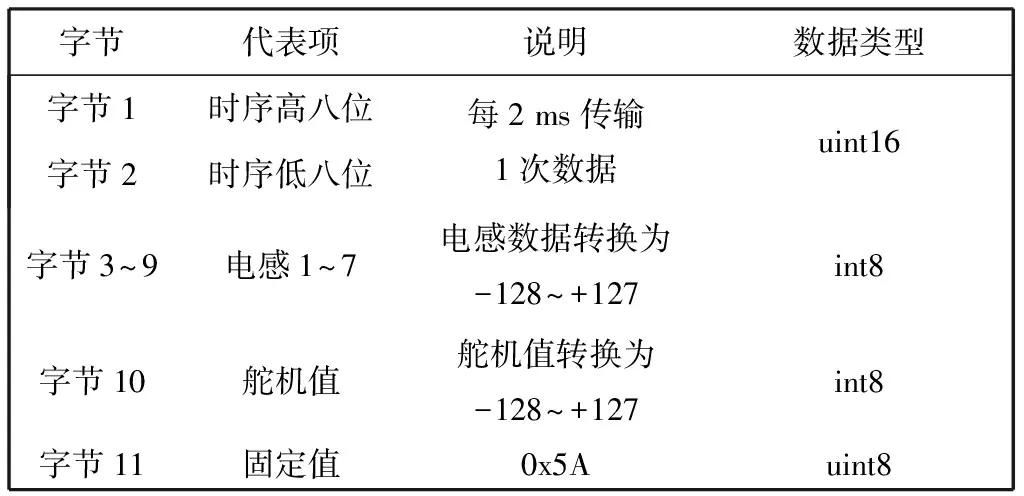
表1 数据格式Tab.1 Data format

一种是手动摆放车模的位置和姿态后，进行电感数据和舵机控制数据采集的方式，该方式可以获得最大偏移角度和最大受控距离下的训练数据. 将机器人放置在直道上，此时机器人正方向与电磁引导线之间的夹角为0°，采集初始姿态的AD值和舵机值；然后向左旋转机器人，使机器人正方向与电磁引导线之间的夹角为1°，采集此时姿态的AD值和舵机值；依此类推，当机器人正方向与电磁引导线之间的夹角为45°时停止采集. 同样，向右旋转机器人，使机器人正方向与电磁引导线之间的夹角为1°，采集此刻姿态的AD值和舵机值；依此类推，当机器人正方向与电磁引导线之间的夹角为45°时停止采集. 利用这种静态采集数据的方法，分别采集机器人在弯道、十字、环岛的数据.

另一种是动态采集数据的方式. 该方式利用传统算法引导机器人识别路径，在机器人控制算法中设置每隔3 s单片机睡眠0.5 s，机器人在睡眠期间不受控制，待算法唤醒后，传统算法继续控制机器人，采集机器人在此运动状态的AD值和舵机值. 虽然这种方式更加符合实际情况，但是由于机器学习的不可解释性，错误的数据或不合适的数据会导致机器人发生不可预知的行为，因此在整个过程中需要进行多次尝试和调整.

经过反复尝试，最终选择第一种方式对机器人方向控制系统进行数据采集，并将数据集划分为直道、弯道、十字和环岛四种类型.

3.3 模型部署

本文在TensorFlow和keras平台上对模型进行训练试验，硬件配置为Intel Core i5 1035G1处理器和16 G内存，模型中各层的学习率为0.01，使用Adam优化器训练120个迭代期，第一次估计的指数衰减率(beta1)为0.9，第二次估计的指数衰减率(beta2)为0.999. 模型预训练时的loss损失函数如图7 所示.

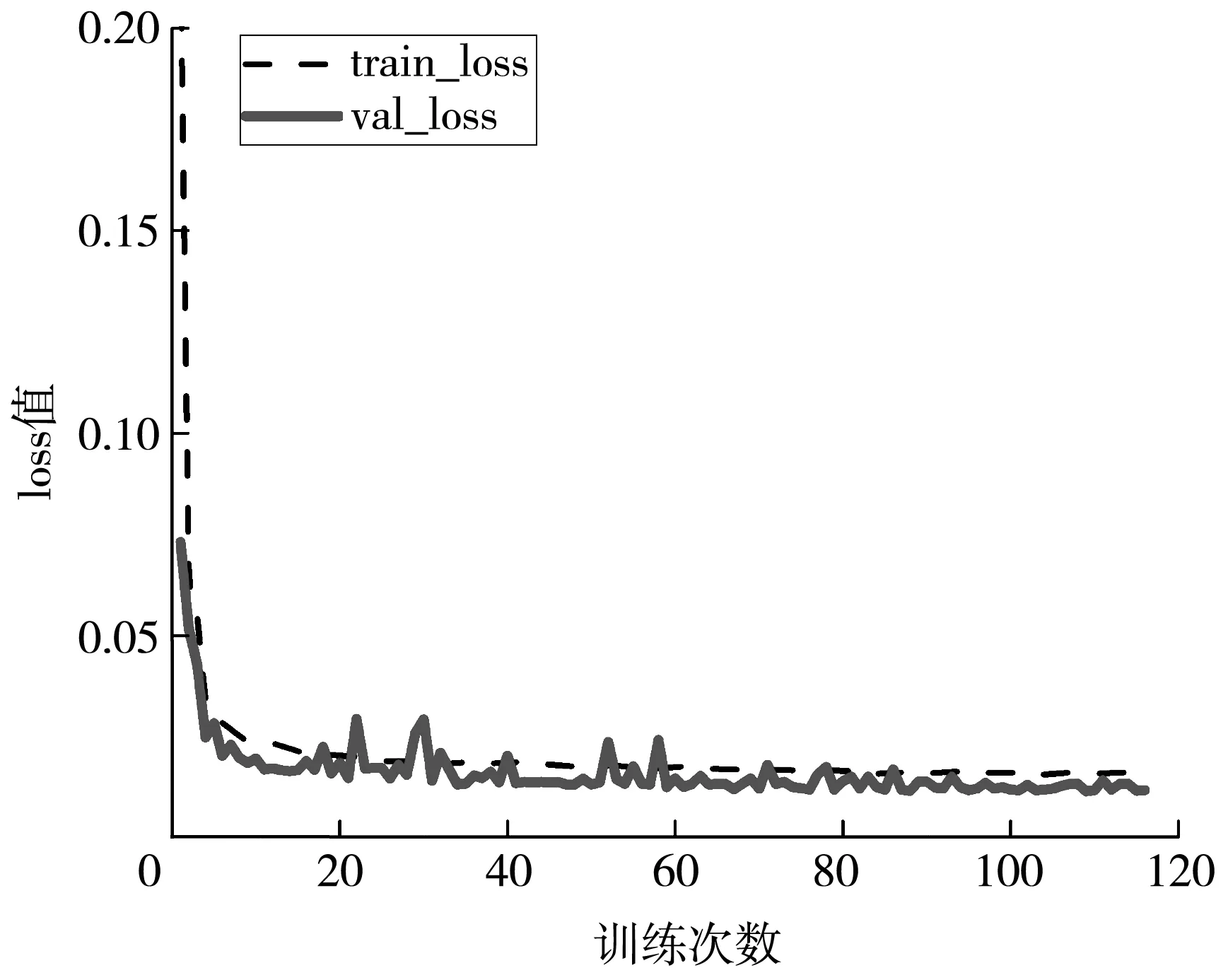
图7 模型loss曲线Fig.7 Model loss curve

由图7 可知，预训练开始时，模型的收敛速度较快，随着训练次数的增加，模型的收敛速度逐渐降低，最终loss值在0.01上下波动.

为了简化模型和对网络模型进行加速，引入NNCU工具来量化模型，为了防止模型运算期间的乘累加溢出，本文采用14位量化，未使用的2个位自动做有符号扩展. 本文中模型的输出范围为(-1,1)，因此，需要将MLP神经网络输出的结果处理成范围为(-128,128)的数据，最终使用14位中的10位来表示该数据.

4 实验分析

图8 为磁导航机器人方向控制系统实物图，系统将英飞凌单片机作为主控，主频达到200 MHz，用于采集信号的电感传感器两两对称放置在车的前面. 电感传感器采集周围的磁场信号后，利用英飞凌主控芯片对信号进行滤波，并将得到的数据按照一定的数据格式传送到PC端. 由PC端对数据进行处理，将PWM值作为模型的输出值，7路电感传感器的采集值作为模型的输入值.

利用测试直道、弯道、环岛和十字赛道所得数据，对MLP神经网络算法和传统PID算法进行对比，分别对直道、弯道、十字和环岛进行100次实验，记录100次实验中正确识别对应路径的次数，最终得到两种算法对复杂路径识别的准确率，如表2 所示.

表2 两种方法路径识别的准确率Tab.2 The accuracy of path recognition in two kinds of method %

图8 系统实物图Fig.8 System physical drawing

通过两种算法的对比，发现在直道和弯道中两种算法的优劣相差无几，但随着路径复杂度的增加，神经网路的优势逐渐体现出来，即神经网络识别的准确率无明显下降，由此得出MLP神经网络在复杂路径识别方面优于传统算法.

为了检验模型训练的效果，将长前瞻电感采集的值解算出的PWM值与短前瞻电感采集的值输入神经网络预测的PWM值进行对比，结果如图8 所示，可以看出，长前瞻电感对应的PWM值与神经网络预测的PWM值基本保持一致.

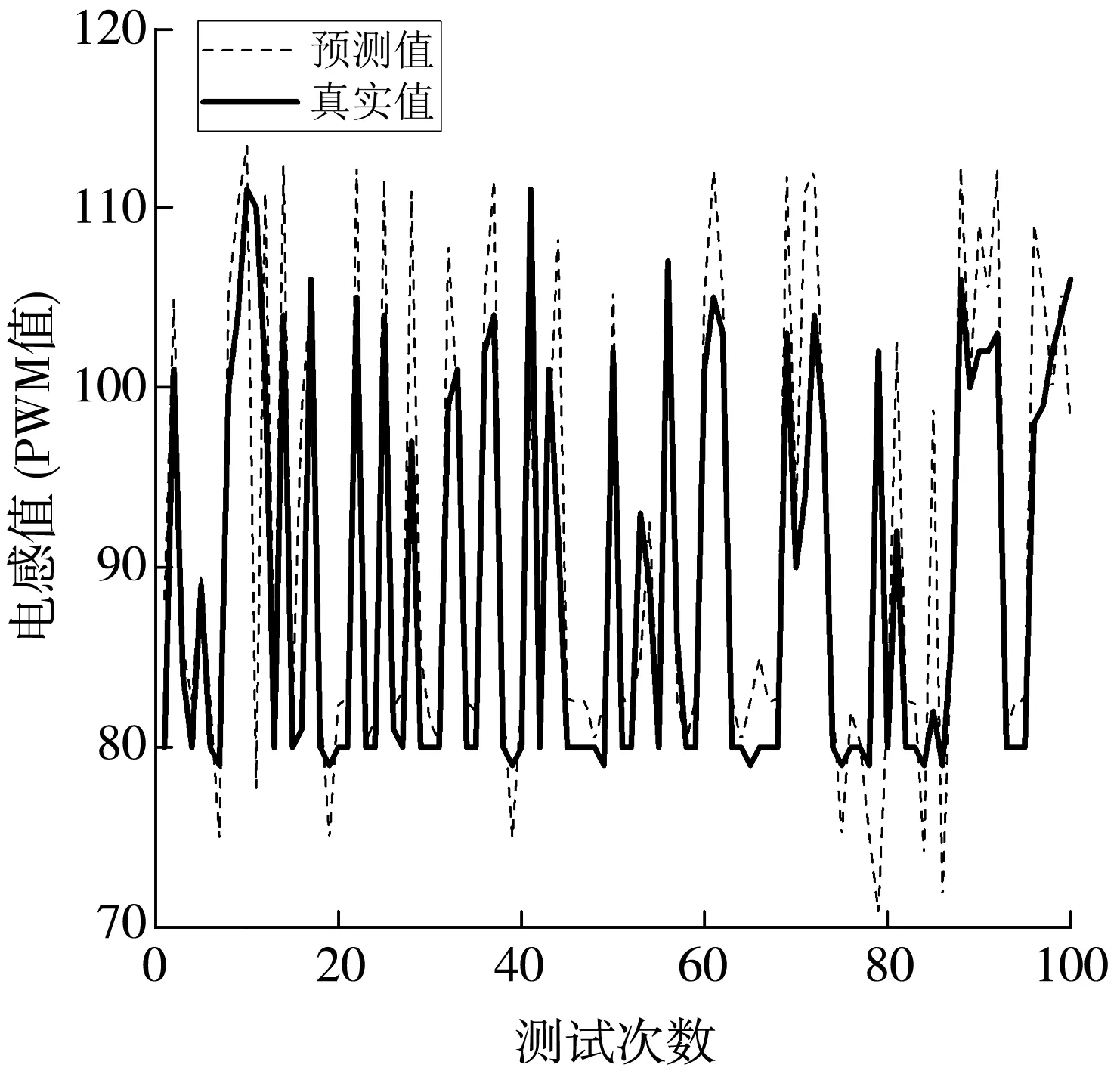
图9 MLP网络模型的预测波形图Fig.9 Prediction waveform of MLP network model

将MLP神经网络模型部署到英飞凌MCU中，不仅可以提升复杂路径识别的准确率，还可以使模型训练不再只依托于PC机. 本试验模型的运行速度达到505 μs，对比舵机控制频率50 Hz(即舵机反应速率为20 ms)可知，MCU在部署MLP轻量化模型后完全可以对系统进行实时控制.

5 结 论

本文分析了多磁场耦合情况下路径识别准确率较低的问题，并提出将MLP神经网络部署到MCU来提高复杂路径识别准确率的方法. 本文利用的MLP神经网络在直道、弯道、十字和环岛四种路径下的识别准确率分别为95%，93%，91%和87%，均高于传统PID算法对应路径的识别准确率. 本文中的MLP神经网络运行速度为 505 μs，满足系统对实时性的要求. 下一步考虑将MLP神经网络部署到国产RT-thread实时操作系统中，并进一步完善MLP磁导航方向控制系统.