流量拥堵空域内一种基于Q-Learning算法的改航路径规划
向征,何雨阳, 全志伟
(中国民用航空飞行学院空中交通管理学院,广汉 618307)
近年来,随着国民经济的稳定增长,中国的民用航空交通运输行业也欣欣向荣,航班架次逐年递增。然而,随之而来的便是空中流量急剧增加与空域资源有限的矛盾,导致了难以估量的社会经济损失,还诱发了严重的安全隐患,造成飞行事故或者事故症候,成为制约民航业发展的痼疾。因此,针对流量拥堵空域内的航空器改航路径规划研究迫在眉睫。在此情况下,原有的部分空中交通管理规则和概念不再适用于如今新时代的运输环境,为了突破这一瓶颈,2004年,欧洲率先提出了欧洲单一天空空中交通管理研究规划(single European sky air traffic management research, SESAR),随后美国又紧接着提出了新一代空中运输系统(next generation air transportation system, NextGen)[1],而在2012年国际民航组织将二者的内容进行整合加以补充改进,最终提出了全球空中航行计划(global air navigation plan,GANP)[2]等一系列相关的运行概念和航行新技术,进一步在全球范围内使空中交通管理体系在安全性、可靠性、可持续性等方面进行提升,实现改航策略的优化以改善空中延误,为现如今的航迹规划研究奠定了夯实的基础,促进了一系列研究成果的发展。
中外学者针对最优路径的规划开展了大量研究。向征等[3]通过栅格法对雷暴所在的空域进行栅格化,并引入人工势场法,改进传统蚁群算法中的启发信息因子,建立基于多航空器冲突避让的绕飞雷暴区的航迹优化模型。陈可嘉等[4]针对危险天气,以改航路径长度最短为目标,在传统的人工势场法中考虑到中间目标点这一因素,引进相对位置和相对速度等变量,从而建立基于改进人工势场法的动态改航路径优化模型。孙瑜[5]根据航空器路径规划需求,结合改进的A*算法对航空器进行4D航迹的预测,并完成航空器的场面滑行动态路径规划及仿真运行。罗如学等[6]通过改进人工鱼群算法,有效改善了传统鱼群算法中视觉范围固定不变的这一特性,并且改进了拥挤度因子函数以提高算法的收敛性,从而提高机器人路径规划的合理性。李少波等[7]探析了遗传算法的优缺点,并对其在机器人路径规划应用领域进行了深入的研究,阐明了现如今需要突破的技术难点,对其发展趋势进行了预测。朱永强等[8]对于机器人路径规划问题提出了一种基于A*算法的改进蚁群算法,首先利用A*算法寻找一条最短路径作为较优解,再提高其信息素浓度,从而有效证实了该改进蚁群算法路径寻优效果更好。赵元棣等[9]在危险天气条件下基于A*算法对进场航空器分别进行静态和动态的改航路径规划,并用仿真实验证明其可行性和有效性。李楠等[10]基于改进的A*算法建立航空器场面滑行最短路径规划模型, 并考虑到航空器的场面滑行时间及相应油耗,结合启发式搜索建立了多目标速度剖面模型, 获得航空器场面滑行的4D轨迹。李志龙[11]针对冲突热点提出了基于改进Q-Learning和基于改进A*的航空器场面滑行的静态路径规划算法,并对这两种场面路径规划策略进行分析比较,建立了基于冲突热点等级分配的动态路径规划模型,以便更加合理地规划滑行路径。魏彤[12]针对航空器起飞前的静态块状受限区和静态带状受限区,分别基于MAKLINK图和多边形法建立改航环境模型,应用改进遗传算法获得全局最优路径。并建立基于最小二乘法的强对流天气短时移动预测模型,通过马尔科夫决策过程模型推算在强对流天气条件下的航空器可航状态概率,从而完成改航路径动态规划。李海等[13]建立一种针对多种危险气象的分层航迹动态规划模型,通过稀疏A*算法对分层的改航空域进行全局航迹规划,并结合动态窗口法对全局航迹进行分段的实时航迹动态规划。疏利生等[14]根据航空器滑行规则建立基于强化学习的静态的机场场面滑行路径优化模型,并通过Off-Policy中Q-Learning算法进行求解。
综上可知,目前路径规划是研究热点,尤其是针对航空器的路径优化模型方面。前人研究主要是对危险天气情况下的航空器改航路径规划,或是机场场面滑行最短路径规划。如今,飞行流量激增导致空域资源的紧张,造成航班延误率不断攀升。而对于如何优化空域结构调整空中流量,有效实现航空器在流量拥堵空域内的运行畅通这一关键研究领域,却鲜见报道。因此,对于流量拥堵空域内航空器改航路径规划的研究势在必行。
动态路径规划模型一般对于航空器运行过程中的实时路径规划具有良好的适应性,目前大多都是建立动态路径规划模型或者动静态路径规划相结合的模型。而航迹规划算法则普遍采用智能优化算法,如粒子群法、遗传算法和A*算法,或者在此基础上加以改进并结合4D航迹进行路径优化。随着人工智能第三次浪潮的到来,学者们将目光投向深度学习或者强化学习等,并将其结合起来应用于航空器的改航路径优化。
基于此,根据航空器在航路阶段流量拥堵空域内的实际运行状态,利用智能优化算法将强化学习中马尔科夫决策过程模型的奖励函数加以改进,对流量拥堵程度不同的航路点进行划分,利用Q-Learning 算法求解模型时,采用ε-greedy策略选择动作来平衡好最优动作和非最优动作之间的关系,其中ε∈(0,1),表示非贪心选择的概率,即随机选择所有动作(包括最优动作和非最优动作)的概率,而剩下1-ε的概率采取贪心策略,即只选择最优动作。如此一来便可保证航空器在寻找最优动作的同时也具有一定的随机性,使得算法更具有合理性。
首先应用栅格法将空域环境进行描述,再根据强化学习中的马尔科夫决策过程模型和Q-Learning算法,结合ε-greedy策略选择动作,研究一套减少空中延误时间、避开拥堵的基于流量管理层面的改航路径优化算法,以有效辅助各级管制员进行决策指挥,减轻其工作负荷,提高运行效率,对空中交通流量管理进行创新性的探索,使空中交通更加安全、有序和高效地流动。
1 空域环境建模
最优路径的规划通常可以划分为空域环境建模和最优路径搜索两部分,采取合理的空域环境建模方法可以极大地提高最优路径的搜索效率。目前主要的环境建模方法有栅格法、可视图法和拓扑法等。而其中的栅格法因其强大的数据处理能力,在里程统计、模糊预测和路径规划等各种模型求解和算法设计上得到广泛应用,成为当前较为常用的建模方法之一。栅格法的核心思想是将空域环境离散分解化,通过相同尺寸和大小的栅格对整个空域进行二值化的综合分割,来量化空域环境的复杂程度,从而提高模型和算法的准确性、灵活性和搜索效率。鉴于驾驶员的操纵难度以及管制员的工作负荷等因素,只考虑同一飞行高度层的改航,因此仅在二维栅格上对空域环境进行建模。二维栅格化分析时需要考虑以下3点。
(1)栅格地图形状大小问题。所构建的栅格地图形状采用的是最简单的正方形,而栅格地图大小设定为10×10。
(2)栅格地图中的栅格尺寸问题。栅格的尺寸大小直接影响后续数据处理的可靠性和使用性,因为网格尺寸过大会影响最终的结果精度,可能导致搜索出来的最优路径的准确度降低,而网格尺寸过小又容易导致数据冗余。根据经验,所有空间化的栅格尺寸统一选取为20 km×20 km,所以栅格地图的实际覆盖面积为200 km×200 km,将格网化的矢量结果转为栅格格式。
(3)栅格的标识问题。将空域环境按照一定的规模划分栅格后,每个栅格都需要进行标识。本文采用坐标法进行标号,由圆锥投影法转换成二维笛卡尔直角坐标系,每个栅格可用坐标进行唯一表示,记为xij=(i,j)。其中,i为栅格所在行数,j为栅格所在列数,如图1所示。
使用二维栅格法选取规则的矩形空域环境进行建模,用来描述某一时段内的流量拥堵空域,且短期内该空域的航路点流量情况基本保持不变。每个栅格代表一个自由区域或限制区域,且每个区域最多含有1个航路点。其中黑色栅格表示限制区域,在限制区域内存在航路饱和点。在这里定义一个新的概念,航路流量饱和点是指单位时间内航空器流经该航路点的流量不小于其自身容量,即该航路点上的流量达到饱和状态,容易造成航空器拥堵。白色栅格和灰色栅格表示为自由区域,在自由区域内没有航路饱和点,即在自由区域内流经该航路点的流量小于其容量,或者该区域内根本就没有航路点。自由区域又可划分为两类,一类是在自由区域内没有航路点或流经该航路点的平均流量不超过容量的80%,为流量较小的自由区域,显示成白色栅格;另一类是该流量大于容量的80%的航路点为繁忙航路点,是流量较大的自由区域,呈现为灰色栅格。而飞机仅能在自由区域内飞行,不能通过限制区域。本文设定空域的起点为(1,10),终点为(10,1),并随机选定几个流量拥挤航路点,如图1所示。
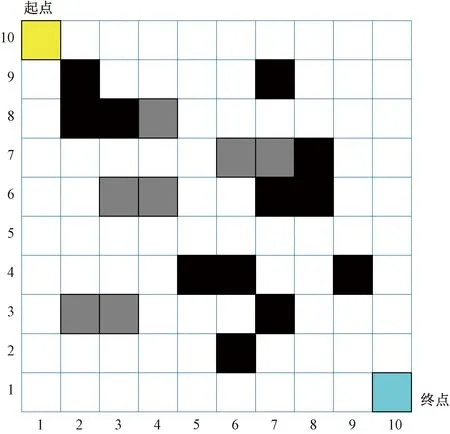
黑色栅格为限制区域;白色栅格和灰色栅格为自由区域
2 马尔科夫决策
强化学习(reinforcement learning, RL),属于机器学习中的领域,是实现人工智能的一种有效手段,在很多领域应用十分广泛,而马尔科夫决策过程(Markov decision process, MDP)是强化学习中的一种常见模型。
马尔可夫决策过程强调如何基于环境而行动,在智能体在与环境的交互过程中获得相应的奖励用以指导动作,通过学习策略从而使得奖励最大化。这种从环境中获得的奖励是一种反馈信号,是作为一种对智能体所采取动作好坏的度量或评价,间接加强使智能体获得尽可能大的正奖励这一趋势,而不是直接告诉智能体如何采取正确的行为。通过这种方式,智能体依靠自身的经历进行学习,在行动-评价的环境中获得学习信息并更新模型参数,不断地改进行动方案以更好地适应环境,从而使得智能体在任意状态下都能搜索出最优策略以实现折扣奖励之和最大化。
2.1 MDP
马尔科夫决策过程一般用五元组描述, 即M=(S,A,P,R,γ),其中,S为有限的状态集合,R为奖励函数,γ为折扣系数,A为有限的动作集合,a∈A,其中a为具体的某个动作,P为状态转移概率矩阵。
状态转移概率Pss′为智能体从某一时刻的状态s转移到下一时刻的其他状态s′的概率,可定义为
Pss′=p[St+1=s′|St=s]
(1)
式(1)中:St为在当前t时刻的状态;St+1为t+1时刻的状态;p为条件概率。
因此,下一时刻状态s′只受到当前状态s的影响,而与之前的状态无关。
若有n种状态可供选择,那么状态转移概率矩阵P可定义为
(2)
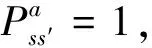
(3)
R为奖励函数,Rs表示在t时刻状态为s的条件下,在下一个时刻所获得的奖励,其计算公式为
Rs=E[Rt+1|St=s]
(4)
式(4)中:Rt+1为在t+1时刻所获得的奖励;E为数学期望。
γ为折扣系数,且γ∈[0,1]。折扣系数反映将来的奖励在当前时刻的价值比例,γ越大,说明考虑越长远,更加重视远期的奖励。
策略π为关于动作集上的一个概率集合,策略π(a|s)表示在t时刻给定状态s的条件下,从当前t时刻的动作集At中选择动作a的概率,而π是在各种状态下选择各种行动的概率分布,是所有状态的π(a|s)共同形成了这个整体策略π,可表示为
π(a|s)=p[At=a|St=s]
(5)
2.2 值函数
Gt为累计奖励,表示从t时刻状态s开始进行状态转移的过程中所有的折扣奖励之和,而且越往后奖励衰减得越多,当t+k+1时刻奖励所对应特定的折扣系数为γk,即此刻的奖励会衰减至原本的γk倍,其定义为
Gt=Rt+1+γRt+2+γ2Rt+3+…+γkRt+k+1
(6)
υπ(s)为状态值函数,是指智能体遵循策略π在某一状态s下所获得累计奖励的数学期望Eπ,表示状态s的价值,而策略π决定了累计奖励Gt的分布,从而会影响状态值函数υπ(s)的期望值,定义为
υπ(s)=Eπ[Gt|St=s]
=Eπ[Rt+1+γGt+1|St=s]
=Eπ[Rt+1+γυπ(St+1)|St=s]
(7)
qπ(s,a)为状态-行为值函数,是指智能体遵循策略π在某一状态s下,选择某一具体动作a所获得的累计奖励的期望,表示在状态s下采取动作a的价值,具体定义为
qπ(s,a)=Eπ[Gt|St=s,At=a]
(8)
Bellman期望方程表示的是υπ(s)和qπ(s,a)自身以及二者之间的递推关系,递推公式如下。
υπ(s)和qπ(s,a)之间的关系可表示为
(9)
(10)
υπ(s)自身的递推关系式为
υπ(s)=Eπ[Rt+1+γυπ(St+1)|St=s]
(11)
qπ(s,a)自身的递推关系式为
qπ(s,a)=Eπ[Rt+1+γqπ(St+1,At+1)|St=s,At=a]
(12)
式(12)中:a′为在下一时刻,即t+1时刻所选择的动作。
2.3 最优值函数
υ*(s)为最优状态值函数,表示从所有策略产生的值函数中最大的那个状态值函数,即
(13)
类似的,q*(s,a)为最优状态-行为值函数,表示从所有策略产生的值函数中最大的那个状态-行为值函数,可表示为
(14)
通过遵循贪婪策略来选择动作,使得q*(s,a)最大化,从而寻找到最优策略。
贪婪策略可表示为
(15)
Bellman最优方程表示的是υ*(s)和q*(s,a)自身以及二者之间的递推关系,结合贪婪策略,递推公式如下。
υ*(s)和q*(s,a)之间的关系为
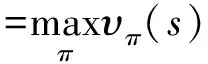
(16)
υ*(s)自身的递推关系式为
(17)
q*(s,a)自身的递推关系式为
(18)
状态s表示飞机在栅格地图中所处的位置,s∈S,S为离散的有限状态集合,状态s可用坐标法进行表示为(i,j),一共有100种状态。其中,经过该空域的过程中起点为(1,10),终点为(10,1),如果飞机到达终点或者航路饱和点,则本次循环结束重新回到起点开始下一次循环。动作a表示飞机选择的飞行方向,A为离散的有限动作集合,a∈A。类似的,可以用(i+1,j)表示飞机向右飞行,用(i,j+1)表示飞机向上飞行,且每次执行动作时只能飞行1个栅格单元,共有4个方向。
当飞机到达终点(10,1)时,执行这一步动作可获得+1 000的正奖励,本次循环结束。当飞机进入限制区域时,系统将会得到-1 000的负奖励。当飞机进入自由区域时,若进入的是灰色栅格,则获得-30的负奖励,若进入白色栅格,系统将会获得-10 的负奖励。这样设置的目的在于寻找的最优策略能够使飞机尽可能地途经流量较小的自由区域,减少或尽量避免通过繁忙航路点的可能性,禁止经过饱和航路点,并且为了能够让Gt较大所以会迫使改航路径更短。根据上述说明可得到马尔科夫决策问题的奖励函数如下所示:
(19)
3 基于Q-Learning算法的最优路径
Q-Learning算法是一种通过不断迭代值函数来逼近最优策略的强化学习方法,是基于时间差分法的离策略学习方法,同时也是目前解决马尔科夫决策问题,广泛应用于路径规划的有效算法。算法的核心思想就是创建一张Q值表,并通过每次循环后的奖励R和Q估计值来更新Q表中的Q(s,a),即qπ(s,a)。待更新完Q值表后,选取该状态下Q值最大,即状态动作值函数最大所对应的动作为最优策略。具体算法原理如下。
步骤1对Q值表中的Q值进行初始化。通常是以随机设定的Q的初始值作为Q值初始表。
步骤2确定当前状态st。
步骤3基于ε-greedy策略根据Q值表选择动作at并执行。ε-greedy策略是一种最常见的随机策略,利用ε-greedy策略来采取行动在迭代足够多次的情况下可以有效避免某些动作的Q值无法更新,使得动作的选择具有一定的随机性。具体来说,飞机有1-ε的概率选择该状态下Q值最大所对应的动作,而对于剩下ε的概率,则采取等概率的方式随机选择任意一个动作,这样就能够平衡好利用(即选择Q值最大的动作)与探索(即选择非最优动作),具体公式为
(20)
式(20)中:argmaxf(x)函数表示使得f(x)达到最大值的自变量,在式(20)中是指使状态-行为值函数Q(s,a)取得最大值,也就是最优状态-行为值函数所对应的动作;|A(s)|为在状态s下所有可供选择的动作数量。
步骤4获得下一时刻状态st+1和相应的奖励Rt+1。
步骤5根据迭代公式更新Q(st,at)。具体的迭代公式为
Q(st,at)new=Q(st,at)old+α[Rt+1+
γmax′aQ(st+1,a′)-Q(st,at)old]
(21)
式(21)中:α为学习率;γ为折扣系数;Q(st,at)old为t时刻在迭代更新之前的状态-行为值函数;Q(st,at)new为在迭代更新之后的状态-行为值函数;max′aQ(st+1,a′)为在下一时刻状态st+1下所对应的最大的Q值。
步骤6若飞机到达目标状态,也就是终点或者限制区域,停止迭代并返回到起始状态,开始新一回合的迭代;否则,将回到步骤2开始继续迭代更新Q值。
步骤7当满足式(21)时,迭代收敛,Q值表更新完成。此时基于贪婪策略根据最大的Q值选择动作,即可寻找最优策略搜索出最优路径。
相应Q-Learning算法流程图如图2所示。

图2 Q-Learning算法流程图
4 仿真运行
通过仿真进行改航路径规划,从而为航空器计算出在某一时段内经过流量拥堵空域时从起点到终点且避开拥挤点的最优路径。仿真空域运行环境为边长20 km、区域为10×10的矩形栅格。其中,黑色栅格为限制区域,表示航路点上存在流量饱和现象,禁止航空器通行。灰色栅格和白色栅格为自由区域,允许航空器经过,并且灰色栅格内的航路点平均流量较高,接近饱和状态,而白色栅格代表区域中的流量较低,航空器飞行较为畅通。
在仿真过程中,令折扣系数γ=0.99,学习率α=0.7。鉴于ε的取值会影响最终生成的航迹,ε取值越大,则说明智能体随机选择动作的概率就越大,相应的,根据Q值表选择该状态下Q值最大的动作这一概率就会减小。为了探究ε的最佳取值,分别给ε以[0.1,0.5]为区间,0.1为步长进行赋值,使ε在不同取值下分别运行10次,计算出生成最优改航路径的长度、拐点和平均响应时间等性能指标,并进行综合比较,从而寻找出一条相对合适的改航路径。其中,空域的起点是(1,10),终点是(10,1),黑线为原标称航迹,如图3所示。
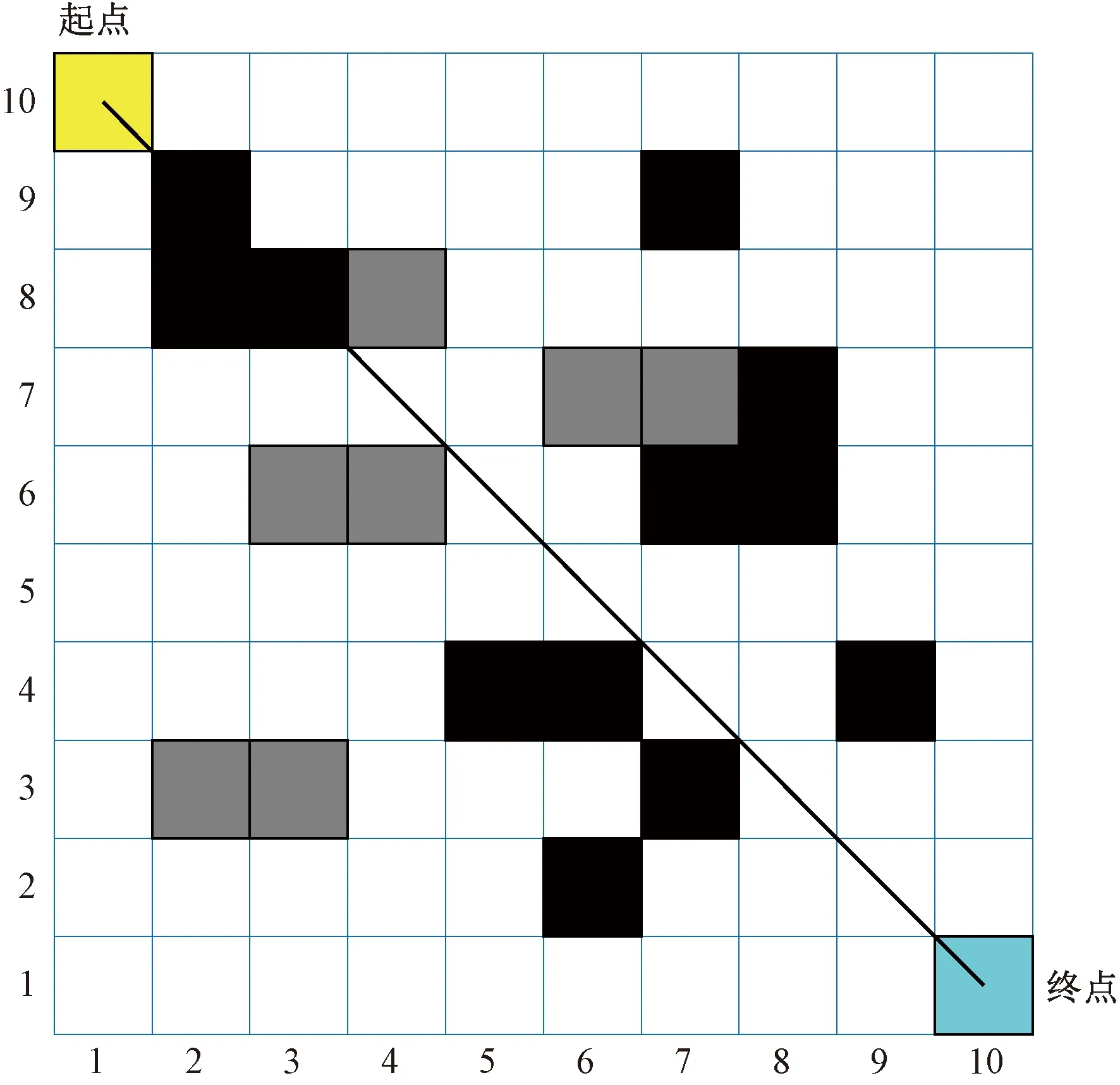
黑线为原标称航迹;黑色栅格为限制区域,表示航路点上存在流量饱和现象,禁止航空器通行;灰色栅格和白色栅格为自由区域,允许航空器经过
如图4所示,红线是ε在不同赋值下的最优改航路径。
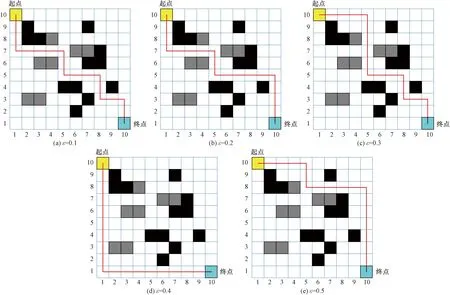
红线为ε在不同赋值下的最优改航路径;黑色栅格为限制区域,表示航路点上存在流量饱和现象,禁止航空器通行;灰色栅格和白色栅格为自由区域,允许航空器经过
鉴于航空器在实际航行过程中应尽量沿原标称航迹飞行,可使其偏航距离(cross track error, XTK)较小,所以将改航路径与标称航迹进行分析对比,并把生成各改航路径相应的性能指标整理出来,结果如表1所示。
分析仿真结果(表1),总结如下。
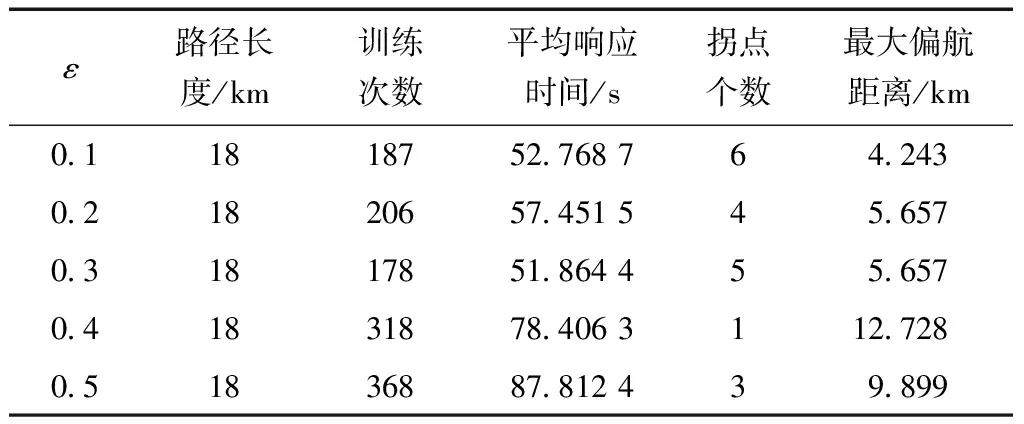
表1 ε不同赋值下的仿真性能指标
(1)观察路径长度的数值变化可知,当对ε进行不同的赋值时,所生成的最优改航路径的长度是一样的。
(2)训练次数和平均响应时间随着ε的增加表现出先暂时波动后显著增加的特点。当ε取值为0.1,0.2,0.3时,完成改航路径规划所需的训练次数均在190±20次内上下浮动,而相应的平均响应时间则都属于(50, 60)这个区间内,其数值相差不大。当ε=0.4时,训练次数和平均响应时间则大幅度增加,而把ε设为0.5时,该数值将会继续呈现明显的增长趋势。而出现这样的现象是因为当ε越大,随机选择动作的概率就越大,也就是探索的概率会更大,那么反过来利用的可能性就随之减少,这样智能体想要寻找出一条最优路径所需要的时间就会大大增加。
(3)通过对比拐点个数和最大偏航距离之间的变化规律可以发现二者之间为负相关关系。当拐点个数增加时,改航路径就会更加贴合原标称航迹,从而能够减小最大偏航距离。拐点个数增加也会导致转弯次数等量增多,从而不利于管制员的指挥工作,同时对飞机的机动性提出更高的要求,加大驾驶员的操纵难度。因此,想要选择一条合适的改航路径,需要综合考虑平衡好拐点个数和最大偏航距离之间的关系。既要控制拐点个数以保证管制员和驾驶员的工作负荷在规定范围内,又要让航空器尽量沿原标称航迹飞行以免偏航距离过大,使其在临近空域内飞行进而干扰到其他航空器的正常通行。
5 结论
(1)用栅格化的方式对空域运行环境进行简化处理。根据航路点的流量将空域划分为3种不同类型的栅格,分别代表不同拥挤程度的区域。其中,黑色栅格表示空中流量达到饱和的限制栅格,灰色栅格表示该区域平均流量超过实际容量的80%,而其他区域则显示为白色栅格,如此一来便能对空域进行离散化建模。
(2)结合航空器的实际运行过程,采用马尔科夫模型并将其中的奖励进行合理的设置。除了终点的奖励为正值,剩下不同类型的栅格对应不同的负奖励,这样便可保证航空器所飞行的改航路径尽可能更短。并利用Q-Learning算法基于ε-greedy策略进行迭代求解,对ε的取值进行探究,从而寻找出一条较为合适的改航路径。
(3)仿真结果表明:应用该模型和算法能够及时在某一时段的流量拥堵空域内寻找出一条从起点飞往目标点,且能够远离流量拥挤点、缩短空中延误时间的改航路径,且路径长度较短,拐点个数较少,具有良好的响应速度。根据飞行计划、气象信息、航空器发送的广播式自动相关监视(automatic dependent surveillance-broadcast,ADS-B)数据等一系列航行情报计算出相应的实时飞行流量,并结合该空域的实际容量进行飞行航迹的规划,使其能广泛应用于流量管理层面,智能化地为管制人员进行辅助决策,是有效解决空域拥堵的重要方式之一。

