基于格子Boltzmann方法的动水压力下透水沥青路面渗流特性研究
李俊,王辉明
(新疆大学建筑工程学院,乌鲁木齐 830017)
“水损害”作为一种早期病害普遍存在于中国沥青路面公路。调查发现,路面其它病害如唧浆、车辙、裂缝等也或多或少有水的影响,因此“水损害”是一个不容忽视的问题[1]。沥青路面上的降水或融化后的冰在汽车轮载的循环作用下,进入路面孔隙中并持续产生动水压力,降低了沥青黏附性并使其黏结力逐渐减小,最终导致沥青膜从石料表面脱落,沥青混合料则松散、掉粒,进而形成沥青路面的坑槽、变形等损坏[2]。
当前,随着中国海绵城市建设工作的全面展开[3],透水沥青路面的应用也越来越广泛。为了解决透水沥青路面在动水压力下的渗流堵塞等“水损害”问题[4],研究孔隙尺度下水在沥青路面材料中的渗流特性及相关机理已成为关键科学问题。
对于路面渗流问题,传统的研究方式通常假定沥青路面为均匀各向同性材料且渗透系数在所有方向保持为常量。Al-Omari等[5]应用有限差分法估算了沥青路面竖向渗透系数,数值结果与Kozeny-Carman经验公式结果拟合很好。Krishnan等[6]基于太沙基固结理论假定渗透系数与空隙率呈线性关系,得出沥青混合料渗透率是导致沥青混合料水损害的重要因素。周志刚等[7]根据试验和多孔介质流固耦合理论,应用非线性有限元方法,分析了饱水沥青路面在不同荷载下的各力学场量变化模型,并得出不同荷载条件下各计算点的孔隙水压力时程曲线,结果表明:路面承受碗形分布荷载时,更容易受到水损害。李少波等[8]根据实际测量,考虑路面、胎压和水膜厚度等因素的影响得出动水压力与行车速度的关系,并在有压条件进行渗透性试验,结果发现动水压力大大提高了沥青混凝土的渗透性。
综上可知,已有研究多采用宏观唯象方法考察路面渗水性能与空隙率等指标的关系,从微、细观层次分析水在沥青混合料中的渗流特性及机理研究仍比较欠缺[9-12]。格子Boltzmann方法(lattice Boltzmann method,LBM)作为一种介观层次数值模拟方法,因其易于处理复杂边界条件和便于实现并行计算,在多孔介质内流动分析方面应用日益广泛[13-18]。基于此,采用多松弛格子Boltzmann方法,考虑轮压动态变化实际工况,研究不同骨料粒径及空隙率等因素对渗流的影响,为工程设计和应用提供理论依据和参考。
1 多松弛格子Boltzmann方法基本控制方程
LBM是近三十年来发展起来的一种流体系统建模和模拟方法[15],其思想起源是20世纪70年代提出的格子气自动机模型,采用粒子在格子上的速度离散、碰撞和迁移过程来模拟介观层次上的物理运动。随后经众多学者的不断研究改进,以气体动理学和统计物理为理论基础,通过引入平衡态分布函数、线形化算子逼近、动理学演化律等,形成了当前广泛采用的Boltzmann方程形式,并且可以证明,通过Chapman-Enskog多重尺度展开分析,可以推导出流体宏观运动的动量方程,即Navier-Stokes方程。
LBM包括流体粒子的离散速度集合、格子结构和演化方程3个要素。大量研究和应用实践表明:D2Q9模型是分析计算二维流动问题的常用优化算法,因此采用D2Q9模型,如图1所示。
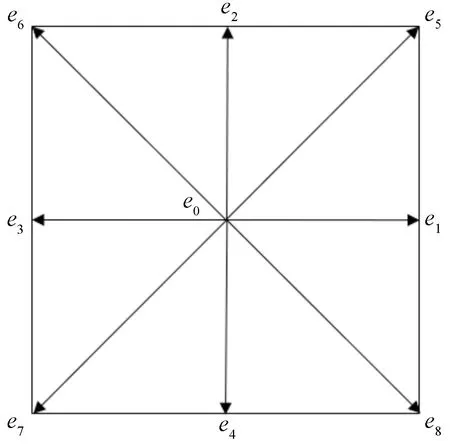
图1 二维空间中9个离散速度的D2Q9模型
离散速度可表示为
ei={(0,0),(1,0),(0,1),(-1,0),(0,
-1),(1,1),(-1,1),(-1,-1),(1,
-1)}c,i=0,1,…,8
(1)
式(1)中:格子声速c=1。
多松弛LBM演化方程为[15]
f(x+eiδt,t+δt)=f(x,t)-M-1[m-meq]
(2)
式(2)中:f为格子节点上的速度分布函数;t为时间步;m为矩;meq为矩的平衡态;M为一个正交的转换矩阵,且有
m=Mf, 即f=M-1m
(3)
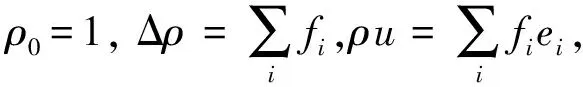
在D2Q9模型中,矩空间元素为
m=[ρeεjxqxjyqypxxpyy]T
(4)
式(4)中:e为运动能;ε为运动能的平方项;jx和jy为动量分量;qx和qy为能量分量;pxx和pyy为对称的黏性应力张量;动量jx和jy是局部守恒的,其他6个不守恒量的松弛过程可描述为
(5)
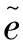
参数e、ε、qx、qy、pxx、pxy平衡态时的取值可表示为
(6)
平衡态时的分布函数表达式为
(7)
权重系数wi取值为
(8)
松弛矩阵S为
S=diag[0SeSε0Sq0SqSvSv]
(9)
其中各个松弛参数表示对应式(4)矩函数m中不同元素的松弛时间,不同的矩可以使用不同的松弛时间[15]。
在多松弛模型中,剪切黏度ν和体积黏度ζ分别表示为
(10)
式(10)中:松弛参数Sν和Se依据流体的剪切黏度ν和体积黏度ζ确定取值,其他的两个松弛参数Sq和Sε可以视为自由参数,用来提高边界条件的精确性和计算的稳定性。计算时参考文献[15],Sq=1.5,Sε=1.4。
2 透水沥青路面结构特征及细观模型建立
2.1 透水沥青路面的结构特征
透水沥青路面与常规沥青路面相比,有着不同的结构和水流动特征[11]。沥青混合料设计空隙率高,一般为18%~25%,空隙大小比较一致,结构主要取决于集料,采用间断级配,可以严格控制集料大小和组成,所含细集料极少,形成骨架-空隙结构,结合料采用高黏度沥青,沥青用量较少。参考文献[11]确定透水沥青混合料的级配范围如表1所示,确定油石比和空隙率如表2所示。

表1 透水沥青混合料的级配设计

表2 油石比和空隙率
透水沥青路面水流动特征是雨水不是通过路面表面水平方向排走,而是通过路面材料竖向渗入到土基里,路面内部发生渗流时以竖向为主。在渗水性能上表现为各向异性,沿沥青混合料厚度方向的渗水性能远远大于其横截面内的渗水性能,横截面内的渗水性能沿行车方向和垂直行车方向基本相同[12]。
2.2 透水沥青路面材料细观模型建立
粒径<2.36 mm的细集料、沥青及填充料统称为沥青砂浆。由于沥青砂浆细观结构极为复杂,要精确描述细微颗粒所需的计算成本极其昂贵,而且在透水沥青混合料中2.36 mm以下粒径的细集料和填充料对混合料骨架结构不起“干涉”作用,其主要作用是填充粗集料间的部分孔隙。因此将沥青混合料视为由粗集料(粒径>2.36 mm)、沥青砂浆(粒径<2.36 mm)及孔隙3种组分构成的复合材料,并将沥青混合料试件作为多孔介质物体进行处理。
建立开级配抗滑磨耗层OGFC-13沥青混合料的二维细观模型,尺寸大小为标准马歇尔试件,即高度为63.5 mm,宽度为101.6 mm,所取计算域能够反映水在透水沥青路面面层内的流动特征。依据前述配合比设计,将粗集料、沥青砂浆等效换算成面积分数相等的相应数量的圆形颗粒。因2.36 mm以下的细集料主要起填充孔隙作用,所以最终根据求出的沥青砂浆面积分数只生成粒径在0.6~2.36 mm的细集料,再根据蒙特卡罗方法,随机生成这些不同粒径的圆形颗粒的投放位置,最终生成二维沥青混合料细观模型。
2.3 边界条件处理
针对上述建立的标准马歇尔试件的二维细观模型,边界条件设置为:上边界即入流边界采用固定压力边界,下边界即出流边界采用充分发展格式,骨料和左右边界采用标准反弹格式[16]。随机生成的二维细观模型及边界条件示意图如图2所示,且格子划分为1 016(宽)×635(高)。
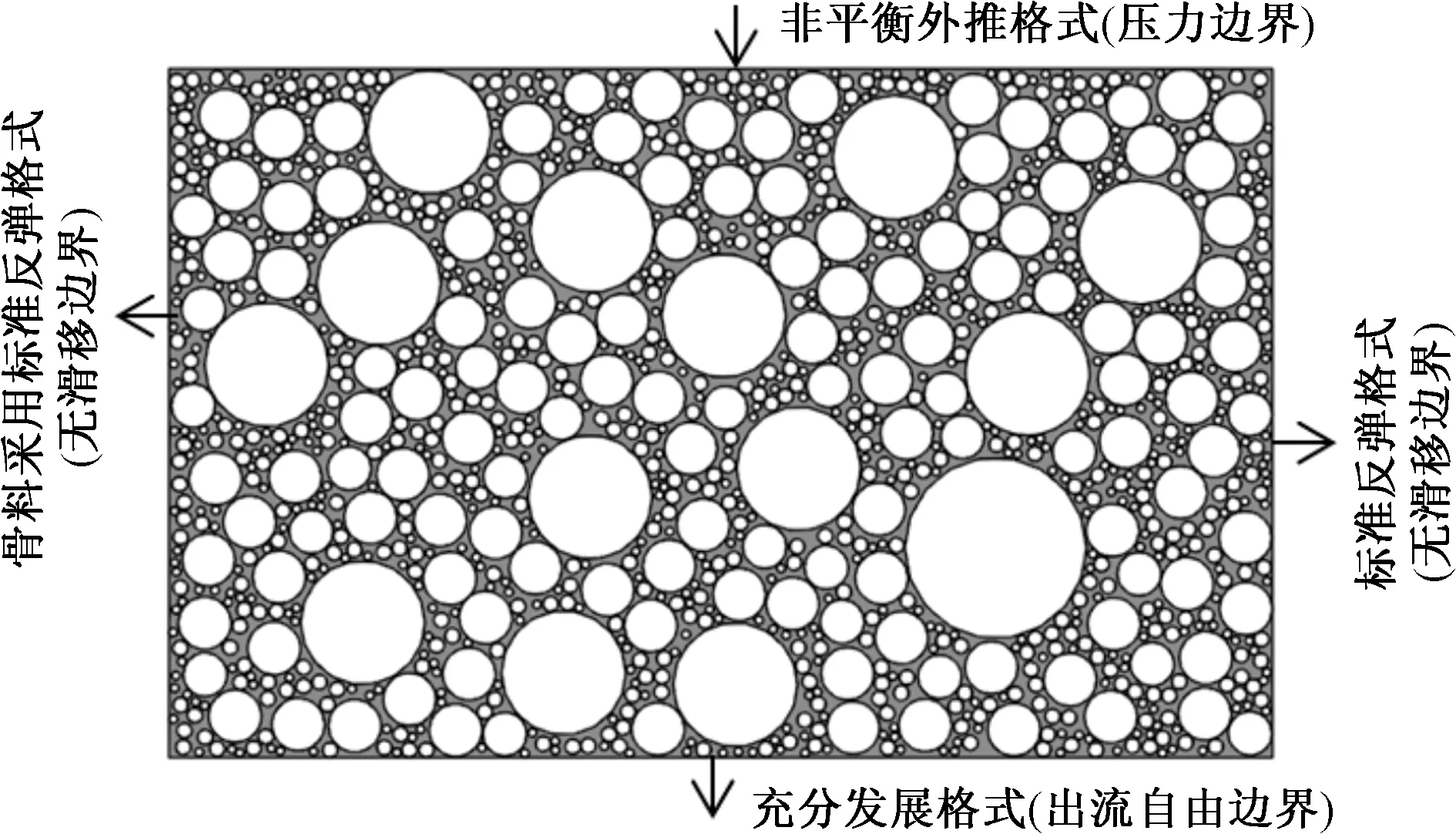
图2 细观计算模型
根据文献[11],马歇尔试件芯样中体积处于0.01~0.1 mm3的空隙只占不到3%,因此网格最小单元大小为0.1 mm时,网格划分方案足够反映颗粒间的空隙。
3 多种因素作用下透水沥青路面材料渗流特性模拟与分析
3.1 动水压力试验测量与计算
李少波等[8]进行了动水压力的模拟试验,测试条件为路面表面纹理构造深度为0.6 mm,水膜厚度控制在3 mm,轮胎为185/70R1386T型,内压220 kPa,并对试验测量数据通过回归分析后得
(11)
式(11)中:pd为动水压力;v为行车速度。
对行车速度不高的普通道路(平均速度为50~60 km/h),行车所造成的动水压力不大,约为9.806 65 kPa,而对高等级公路,行车速度提高到110 km/h,所造成的动水压力则达到普通道路的4倍。
假设对OGFC-13沥青混合料试件施加0~45 kPa的水压差,相当于汽车以0~120 km/h行驶速度时产生的动水压力。
3.2 粒径对透水沥青路面材料渗流特性影响
首先考察集料粒径对透水沥青路面混合料渗透率的影响。在保证其他参数不变的前提下,针对前面选定的第1种配合比,生成工况1和工况2的颗粒数和粒径,两者的差别在于构成沥青混合料的圆形颗粒粒径有所不同;两种工况对应的二维细观模型的粒径范围及圆形颗粒数如表3所示。
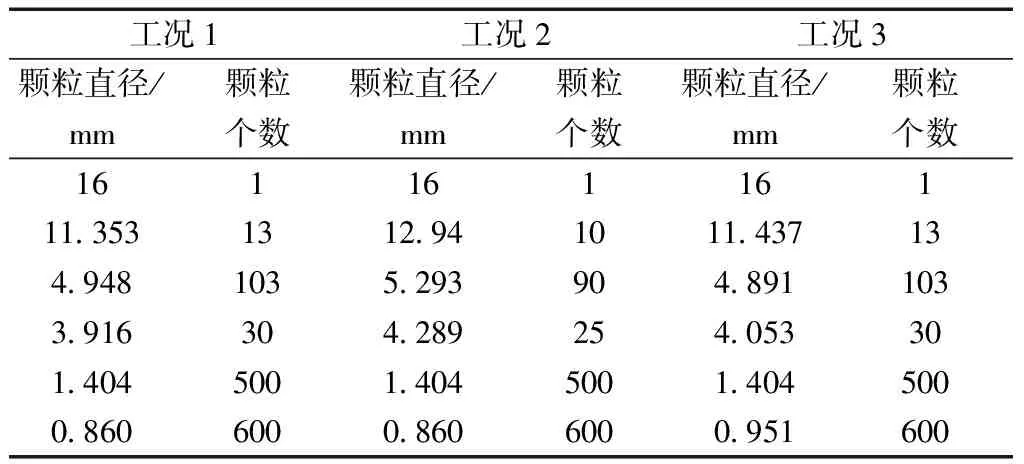
表3 按照配合比生成的细观模型的粒径范围及颗粒数
取动水压力差为1.5 Pa,水的动力黏度取0.001 Pa/s。采用格子Boltzmann方法计算模拟沥青混合料试件内水的流动现象,其速度云图如图3(a)、图3(b)所示,都表现为层流流动,且有流速明显的渗流主通道。
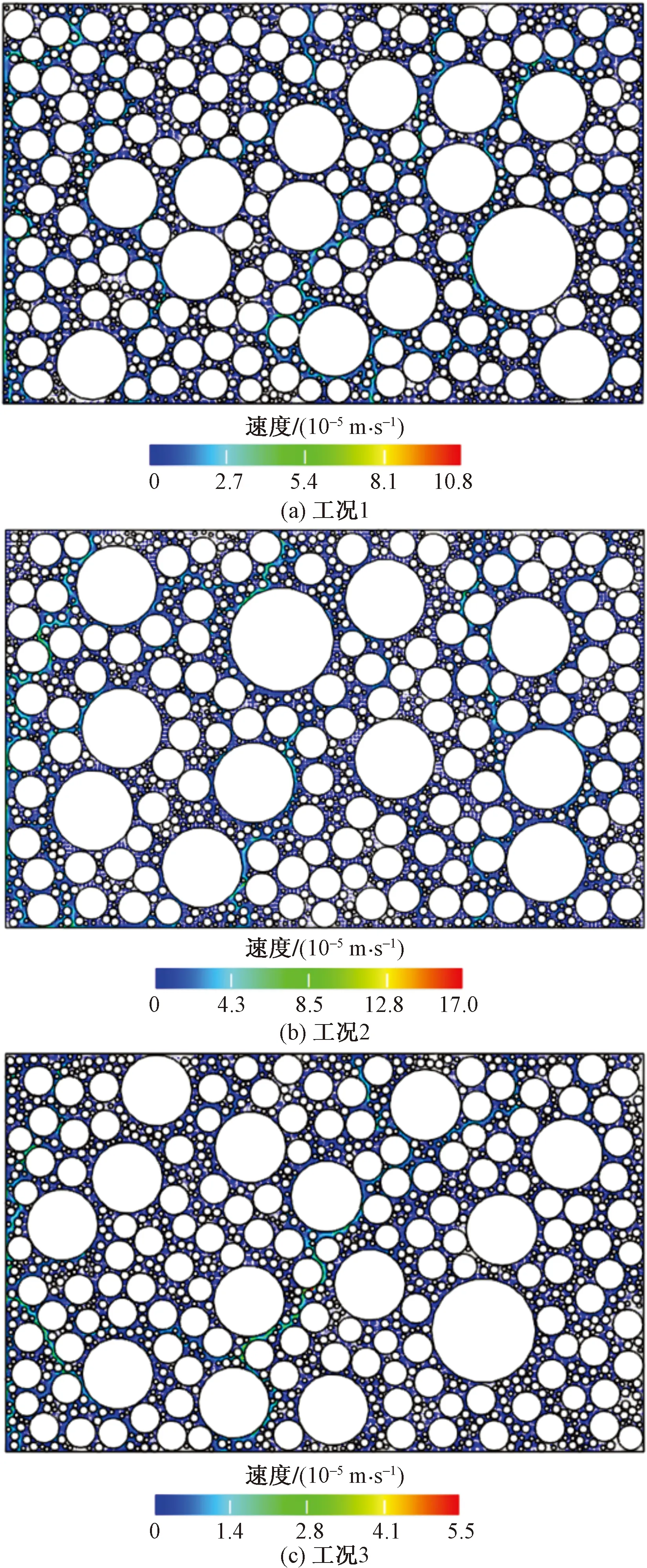
图3 不同工况试件内水的流动速度云图
达西定律被广泛应用于多孔介质内的流体运动,可根据整个流场流体的平均流速、压强梯度和流体动力黏度计算透水沥青混合料试件的渗透率[13],计算公式见式(12)。同时,沥青混合料试件的渗透率也可由经验公式估算,如应用较多的Kozeny-Carman公式[11-12],其具体形式见式(13)。
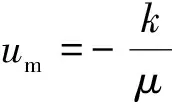
(12)
(13)
式中:um为流体平均速度;k为渗透率;k0为Kozeny-Carman常数,k0=5;C=1/36k0,即对圆形颗粒C取值为1/180;k0=4.166 7,圆形颗粒C取值为1/150;ε为空隙率;r为集料平均粒径;∇p为压强梯度,压强梯度=压差/距离,本文模型的距离为0.063 5 m。
渗透系数又可由渗透率得出,具体公式为
K=kρwg/μ
(14)
式(14)中:K为渗透系数;μ为流体的动力黏性系数;ρw为水的密度,取1 000 kg/m3;g为重力加速度,取10 m/s2。
根据试件内流场计算结果,通过达西定律可以得出沥青混合料的渗透率k如表4所示。此外,结合试件结构特征(空隙率、集料平均粒径),可由Kozeny-Carman经验公式[式(13)]估算沥青混合料的渗透率。从表4的结果可以看出,通过LBM方法和通过经验公式估算的渗透率总体一致,工况1与Kozeng[19]建议公式的误差小于10%,工况2与Ergun[20]建议公式的误差小于20%,说明多松弛格子Boltzmann方法适用于处理透水沥青路面材料渗流问题。造成两种方法结果误差的主要原因在于:经验公式所选的r为平均粒径,以及设计空隙率和实际有效空隙率的差别,LBM方法建立的细观随机模型更多地考虑了不同的骨料粒径和细观结构的有效空隙率,更接近实际真实细观结构。
3.3 空隙率对透水沥青路面材料的渗流特性影响
其次考察空隙率对透水沥青路面混合料渗透率的影响。取动水压力差为1.5 Pa,水的动力黏度μ取0.001 Pa/s。选取工况1(空隙率为22.5%)和工况3(空隙率为21.3%)对比分析,流场计算结果如图3(a)和图3(c)所示,类似可计算出沥青混合料的渗透系数如表4所示。可以看出,空隙率大的透水沥青路面渗透系数更大,渗透性相对更好。
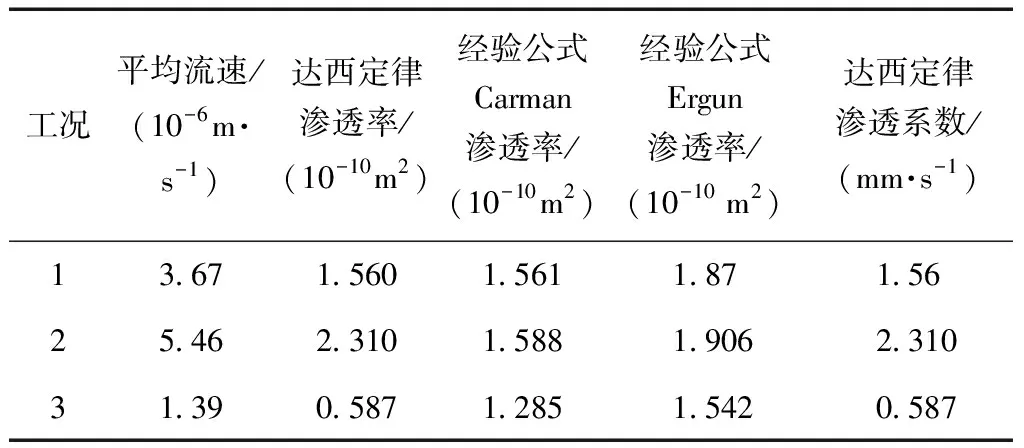
表4 3种工况的渗透率系数
图4为Kutay等[14]对沥青混合料试样渗透系数的实验测定值k1与LBM模拟结果kc进行的比较,进一步证明了LBM方法对沥青混合料渗流特性模拟的可靠性和准确性。
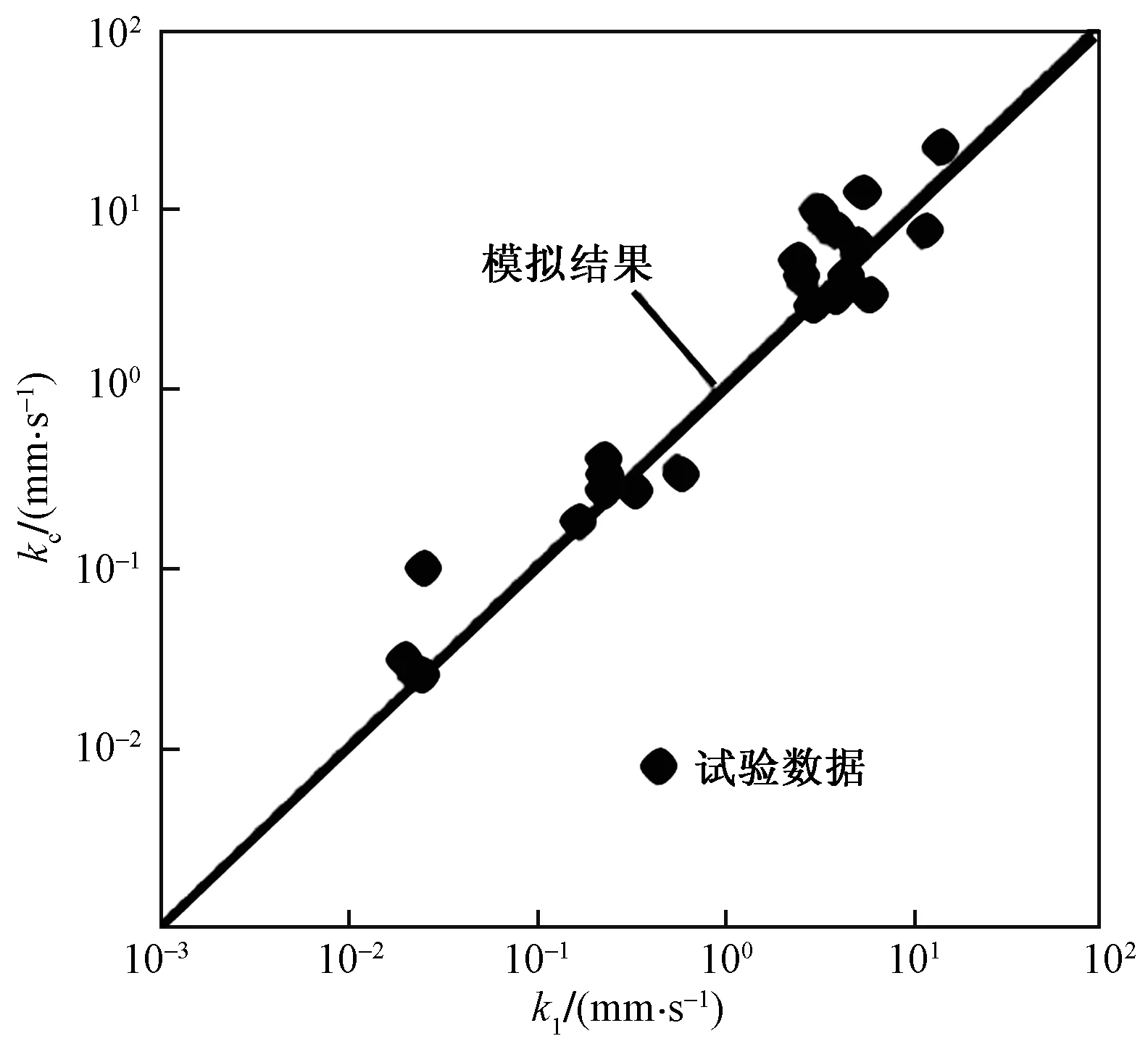
图4 LBM模拟和实验室测定的渗透系数
3.4 动水压力变化对透水沥青路面材料的渗流特性影响
为了考察不同大小的动水压力对透水沥青路面渗透率的影响,针对工况1、工况2和工况3细观模型,取动水压力在1.5~45 000 Pa范围内变化并进行模拟计算,以下仅显示动水压力为1.5 kPa和15 kPa时的流场计算结果,如图5所示。不同大小动水压力对孔隙内平均速度影响表5所示。可以看出,随着动水压力的增大,沥青混合料试件内水的流速也相应增加,当动水压力增大到1.5 kPa后,流速增大的速率开始慢慢小于压力梯度增大的速率,此时3个工况的雷诺数分别为4.04、6.55、1.62。这与目前普遍认可的研究结果[17]:达西定律在砂性土地下水渗流成立的范围在Re小于1~10一致。
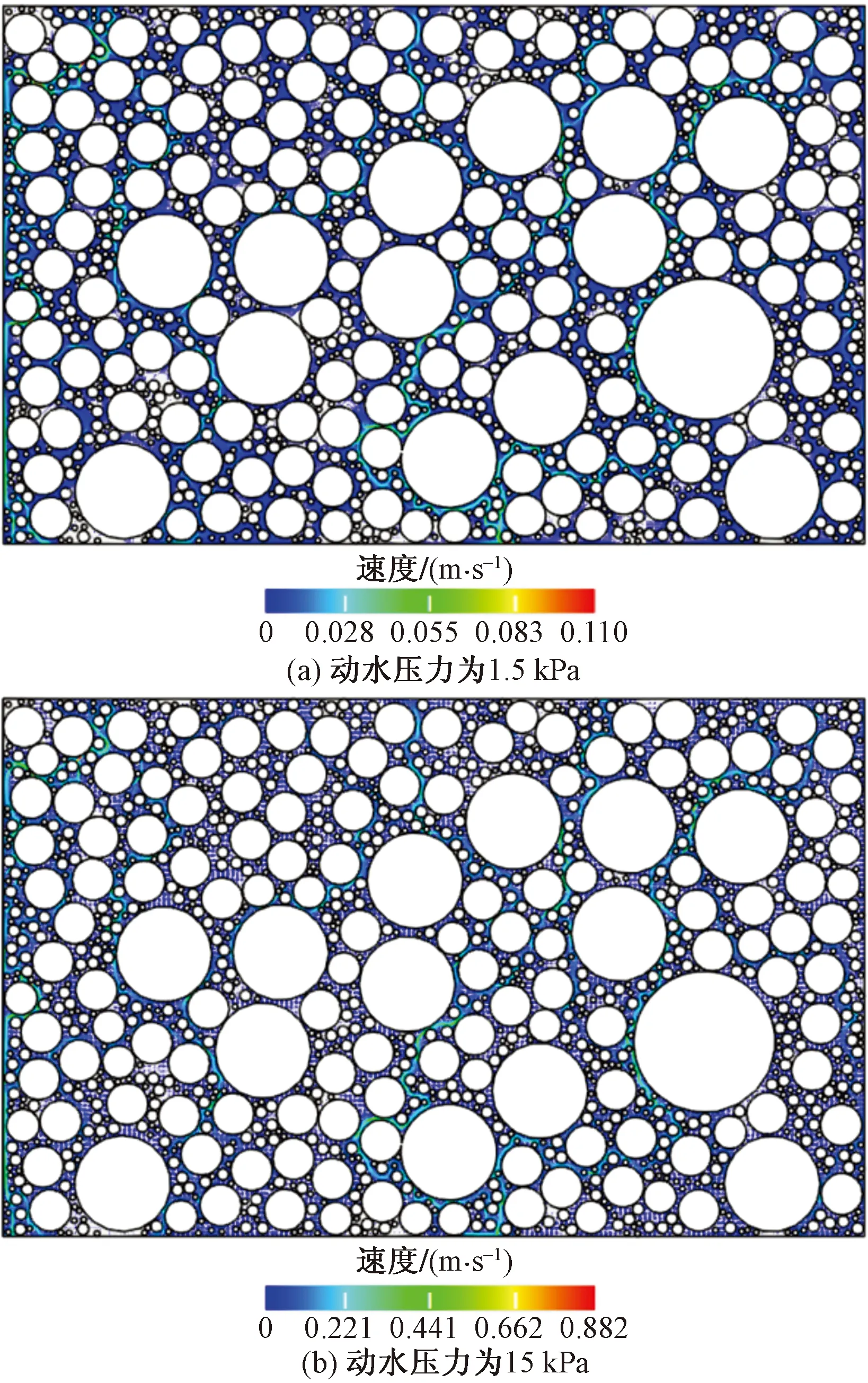
图5 工况1不同动水压力下的速度云图
(15)
式(15)中:Re为雷诺数;um为平均流速;r为平均粒径,取0.001 2 m;v为运动黏滞系数,取10-5m2/s。
以不同大小动水压力下的平均速度为横轴,相应流场的压强梯度值为纵轴,可以将表5中3种工况的压强梯度和对应的平均速度用图形表示并用曲线加以拟合如图6所示。可以看出,在压强梯度小于23 622 Pa/m时,即动水压力差≤15 000 kPa时,平均流速与压强梯度严格呈线性关系,从而基于细观模型内水的流动验证了达西定律的适用性。随着动水压力差的持续增长,当在15 000~45 000 Pa范围内变化时,拟合得到的曲线呈现出弱非线性,这是因为随着雷诺数的增大,水流阻力也在逐渐增大,当Re>10后,多孔介质内部孔隙中的水渗流开始服从非线性渗流规律[17]。

表5 不同动水压力下的平均流速
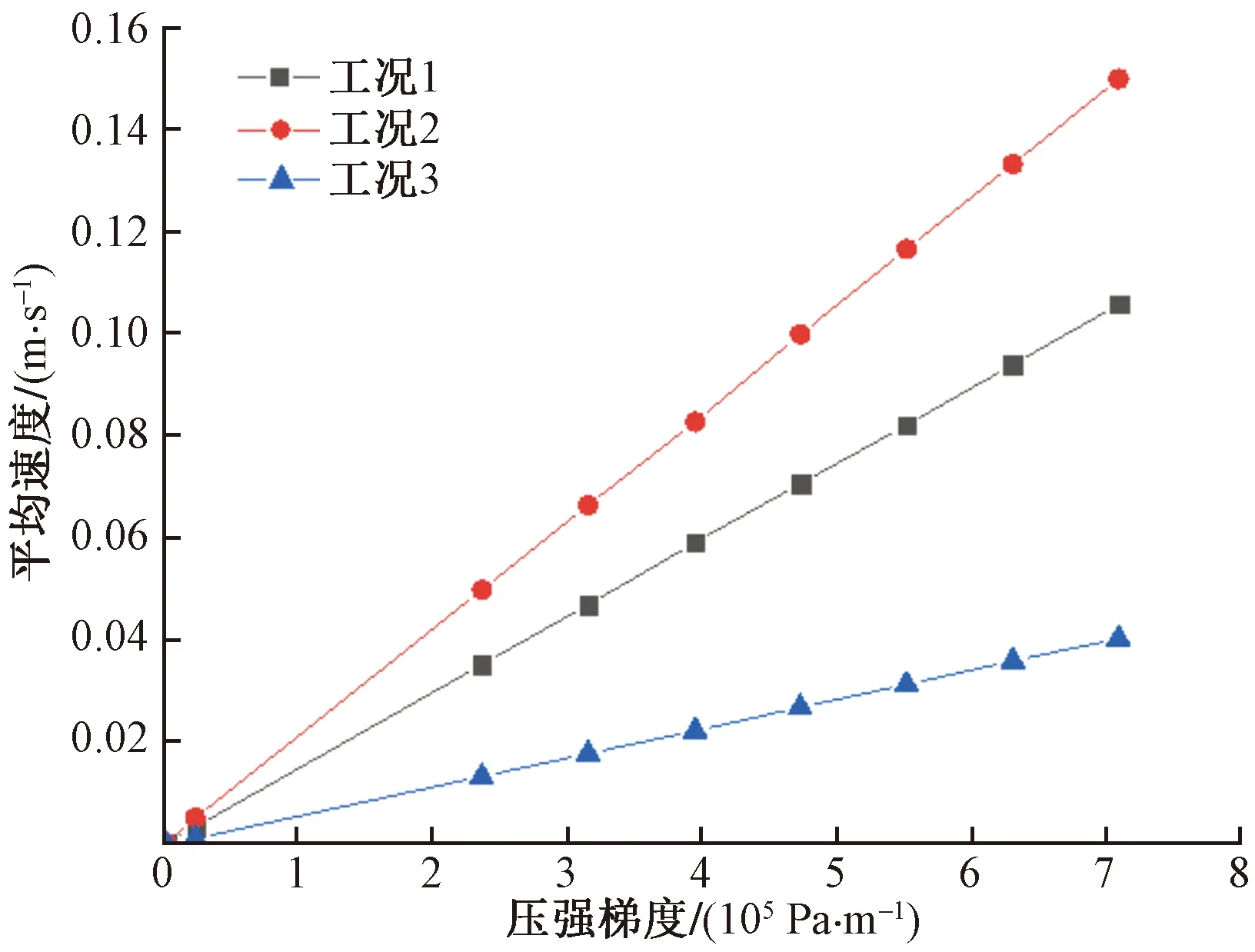
图6 平均流速与压强梯度关系
4 结论
参考实验级配方案,应用蒙特卡罗方法,建立开级配抗滑磨耗层OGFC-13沥青混合料的3种工况二维细观模型。基于多松弛格子Boltzmann方法,从细观层面模拟分析了集料粒径、沥青混合料试件空隙率对透水沥青路面材料渗透系数的影响以及动水压力变化对平均速度的影响,研究探讨水在沥青混合料内部的输运规律。得出如下主要结论
(1)在透水沥青混合料试件空隙率相同的情况下,大粒径颗粒占多试件的渗透系数大于小粒径颗粒占多的试件的渗透系数,空隙率大的沥青混合料渗透系数大于空隙率小的渗透系数。
(2)在外界压力驱动下,水在沥青混合料的流动会有几条主通道,且当压力驱动符合达西定律时,同一种沥青混合料试件内部在不同压力差时流场流速大小区域分布规律趋势一致。
(3)当行车速度在0~120 km/h范围时,造成0~45 000 Pa的动水压力差。随着动水压力的增大,当动水压力差增大到15 000 Pa时,流速增大的速率开始慢慢小于压力差增大的速率。当动水压力在0~1 500 Pa范围内变化时,平均流速与压强梯度严格呈线性关系,验证了达西定律的适用性;当在15 000~45 000 Pa范围变化时,达西定律计算得到的平均速度偏大,这是因为随着雷诺数的增大,水流阻力也在逐渐增大,当Re>10后,孔隙介质中的水渗流服从非线性渗流规律。从而表明由于透水沥青路面的细观结构复杂,即使低雷诺数下也会出现非达西流动。

