砂土中压力分散型锚索锚固机理研究

管昕昉，吕明，陈慈河，周俊杰

(1.同济大学道路与交通工程教育部重点实验室，上海 2018041；2.中交文山高速公路建设发展有限公司，文山 663000；3.中交西南投资发展有限公司，成都 610000；4.中交第二航务工程局有限公司，武汉 430040)

锚杆因其良好的加固效果、低成本、施工方便而被广泛地应用于各种水利水电、公路铁路边坡和隧道等各类土木工程建设和一些灾害事故处理中，如塌方处治[1]。压力分散型锚杆作为一种新型锚固形式，目前对其锚固机理的研究成果[2-5]仍局限于连续介质力学和宏观试验的层次，缺乏对于杆体周围土体细观力学组构演化规律的分析，无法从本质上揭示其细观锚固机理。

目前对压力分散型锚杆锚固理论的数值模拟分析主要采用有限差分法和有限元法，由于土体是一种离散介质，因此采用连续介质力学方法显然是不合适的。文献[6-8]提出了颗粒流理论与其数值模拟方法PFC2D。颗粒流理论作为一种离散单元法的特殊化[9]，它的基本单元是刚性的，其几何形状是球面或圆盘。它特别适用于颗粒介质(如砂粒)的力学性能研究，且能对大变形问题进行模拟。文献[10-12]、文献[13-14]分别采用颗粒流理论和PFC2D(二维颗粒流代码)程序模拟分析了岩土的细观力学性质、双轴试验和风沙桩在上拔荷载下的力学性质。同时，目前对压力分散型锚杆在不同锚杆埋深、砂土密实度等因素影响下的细观锚固性能研究还未见报道。

数码相机的发展以及计算机硬件性能的提高，为岩土锚固室内模型试验的细观应变和位移量测提供了一种简易、经济的方法。数字图像变形量测技术[15]是一种以数字图像的测量技术为基础，利用计算机处理与分析，获得图像中量测点的变形规律。依据数字图像基本构成元素(像素pixel)的颜色[16]，选取初始照片上设置的量测点识别对应点，然后采用图像相关分析方法实现位移测量和应变分析。

通过室内模型试验和数字图像变形量测技术，研究了压力分散型锚杆在张拉荷载作用下的锚固特性以及在不同砂土密实度、锚杆埋深、锚片间距及锚片数量等不同工况下锚固段岩土的位移场和剪应变场；在室内试验的基础上，将颗粒流理论应用于压力分散型锚索锚固工程的数值模拟分析，建立了分析压力分散型锚索锚固性能的颗粒流数值分析模型；通过数值模拟试验，分析了压力分散锚杆在荷载作用下砂粒的细观力学特性，如应力、位移和孔隙率；通过与室内模型试验结果相对比，验证数值模拟的正确性，并通过对锚杆埋置深度、砂体密实度等因素的分析，探讨了影响压力分散锚杆锚固性能的一些因素。

1 模型试验方案设计

1.1 试验装置

试验装置如图1所示，主要包括模型试验槽、半圆形锚片锚杆、高倍自动拍摄数码相机、连接杆、加载装置等。模型箱采用有机玻璃板制成，尺寸为650 mm(长)×300 mm(宽)×500 mm(高)，锚片为半圆形，直径D=50 mm，厚8 mm，锚杆为直径为6 mm的螺纹钢杆，双锚片压力分散型锚杆相邻锚片间距分别为S=1.5D，S=3D，三锚片锚杆相邻锚片间距S=1.5D，如图2所示。

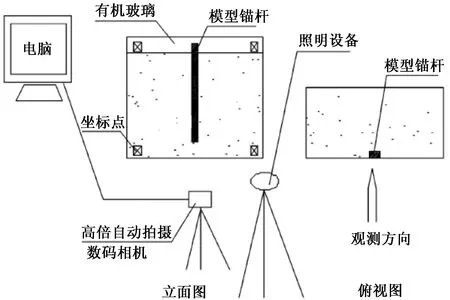
图1 模型试验装置试验图

图2 模型锚杆

1.2 试验方案及布局

为了研究不同砂土密实度和锚杆埋深率下杆周土体的位移场和应变场，揭示杆体周围土体的变形机理，对压力分散型锚杆在两种不同砂土密实度及杆体埋深比H/D分别为3、6时的情况进行拉拔试验(H为埋深)，砂土的物理性质指标如表1所示。本试验主要考虑了不同砂土密实度、埋深、锚片间距、锚片数量条件下压力分散型锚杆抗拔特性及锚周土体的变形机制，试验方案如表2、图3所示。压力分散型锚杆模型试验采用重物(砝码)加载的办法，通过在锚杆顶部安置百分表，实现对锚杆的位移量测。对破坏荷载下的图像进行分析，获得杆周土体的位移场和剪应变场。

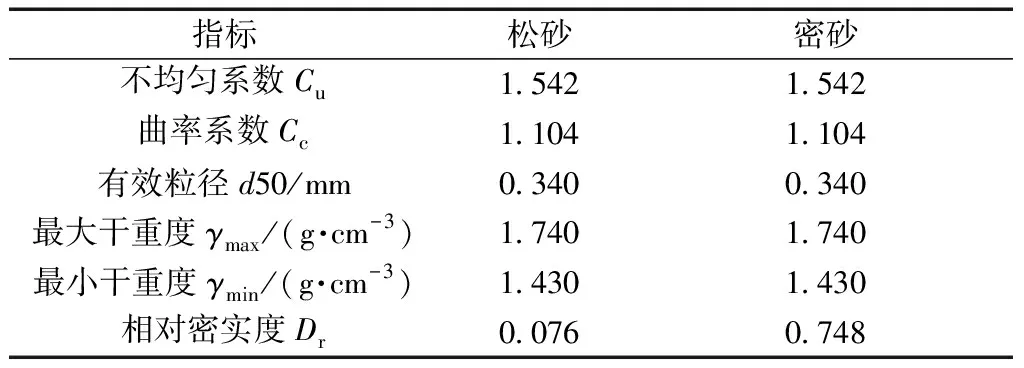
表1 土的物理性质指标

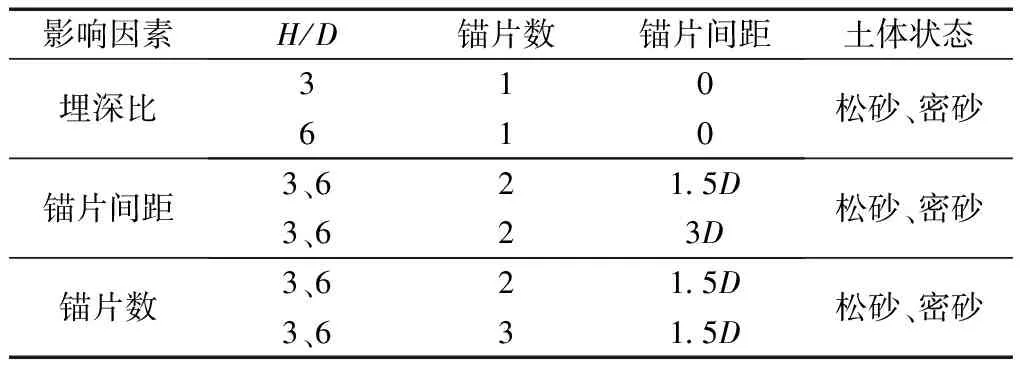
表2 试验方案

图3 室内模型试验

1.3 室内模型试验结果分析

1.3.1 抗拔承载力与位移关系影响因素分析

如图4(a)、图4(b)所示，在相同锚杆埋深率H/D=3的条件下，单锚片锚杆在松砂中的极限承载力为0.8 kN，密砂中为1.6 kN，由此可见，埋深率相同情况下，密砂中锚杆的极限承载力约为松砂中的两倍。对于锚杆在峰值点的位移，当在松砂中达到极限承载力时，锚杆的位移为374 mm，而在密砂中锚杆的相应位移为112 mm，可以看出，松砂中峰值荷载引起的锚杆位移远大于密砂中的锚杆位移。由此可见，砂土的密实度对锚杆极限承载力的影响较大。在相同砂土密实度下，埋深比为3时的锚杆承载力明显小于埋深比为6时锚杆的承载力。图4(c)、图4(d)显示了不同锚片间距下的双锚片锚杆的上拔荷载-位移曲线，当锚片间距为3D时，双锚杆的荷载-位移曲线与单锚片锚杆相似；锚板间距为1.5D的双锚片锚杆荷载-位移曲线在峰值后保持光滑，且在峰值后上拔力显著减小。图4(e)、图4(f)为不同锚片数量下锚杆的上拔荷载-位移曲线，可以看出，在不同砂土密实度下，在双锚片锚杆中加入一片锚片，均可提高锚杆的极限承载力，且在密砂中承载力的提升远大于松砂中，在密砂中，抗拔承载力提高，但破坏位移减小。

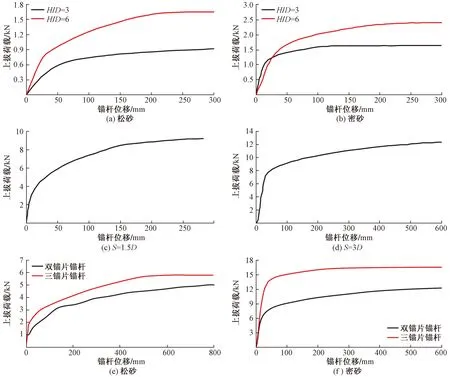
图4 室内试验结果

1.3.2 位移场的发展

图5为经过图像处理软件处理后的压力分散型锚杆杆周土体发生破坏时的位移云图。可以看出，密砂中压力分散型锚杆锚片正上方砂土位移呈现均匀的向上移动，直至贯穿土体表面，锚片两翼处的土体位移向上移动，并以一定角度向外倾斜，位移大小从中间向两侧呈倒梯形分布，逐渐减小。锚片两侧土体相对位移的变化表明，锚片两侧均发生剪切，形成两条对称剪切带。松砂中的压力分散型锚杆位移场与密实砂的位移场明显不同，松砂中的位移场只在锚片上部的局部土体中产生位移，且中间较大，两侧较小，上部较大，上部较小，其影响范围明显小于密砂，没达到土体表面，位移等值线的形状内部类似于锥体，外部向上逐渐变为气球状。

从图5(a)～图5(d)可以看出，在松砂中，对于单锚片锚杆，虽然锚杆的埋深不一样，但在承压板上方形成了一个钟形压缩区，该压缩区的影响范围大致是锚片直径的两倍，结果表明，尽管埋深率不同，但单锚片锚杆周围的土体表现出相似的破坏模式。从图5(e)～图5(l)可以看出，对于双锚片锚杆，当锚板间距为1.5D时，因为锚板间距足够近，锚片之间的土体被向上带动，并随着位移的发展呈现柱状破坏；当锚片间距为3D时，双锚片锚杆和单锚片锚杆表现出相似的破坏模式，双锚片锚杆各个承压板上部的钟形压缩区域小于单锚片锚杆承压板上部的钟形压缩区。在密砂中，可以看出，埋深率为3时的位移场和埋深率为6时的位移场表现出不同的破坏模式，当埋深比为3时，杆周围的土体形成一个倒梯形，并贯穿至土表面的整体破坏。当埋深比为6时，破坏体仅限于土体内部。

图5 锚固结构位移场云图

1.3.3 剪应变场的发展

图6为经过图像处理软件处理后的压力分散型锚杆杆周土体发生破坏时的剪应变场云图。可以看出，在不同的砂土密度、锚杆埋深、锚片间距和锚片数量下的破坏模式并不相同。在松散砂中，当埋深比为3和6时，锚周土体表现出相似的破坏形式和冲切破坏，对于埋深比为3的锚杆，最大剪应变线形成锥形冲切破坏面；对于埋深比为6的压力分散型锚杆，最大剪应变线形成向外扩展的冲切破坏面。在密砂中，埋深比为3和6时，破坏模式有明显差异。对于埋深比为3的压力分散型锚杆，杆体两侧土体存在对称分布的剪切带，在拉拔过程中向地面扩展，从而形成整体剪切破坏，观察可知，剪切破坏面与垂直方向之间的夹角约为45°。然而，对于埋深比为6的锚杆，杆周土体破坏面仅限于土体内部，呈现局部破坏形式。从图6可以看出，当锚片之间的间距为1.5D时，锚片间的土体破坏为柱状破坏，这也解释了室内试验中锚板间距为1.5D的双锚片锚杆荷载-位移曲线在峰值后保持光滑，荷载-位移曲线平滑是因为锚片之间的距离足够近，锚片之间的土体随着位移的发展向上移动，锚片之间的土体不会向侧面和底部滑动，同时第一片锚片底部未出现缝隙，使得其上部土体不会向下塌落，两锚片之间土体的破坏模式为柱状破坏。

2 数值模拟验证

2.1 数值模型的建立

对所研究的问题给出边界范围及颗粒单元的比例级配，首先生成颗粒，在墙体区域内令砂颗粒随机充满，利用对重力进行加载循环来抵消墙体内部非均匀应力。然后对模型的边界进行设计，即锚孔壁，由“墙体”实现，设计400 cm的上下墙高，600 cm的左右墙宽。锚杆的轴向定义为y方向，与之垂直方向定义为x方向。压力型与压力分散型锚杆锚固体系中的钢筋颗粒、承压板颗粒及砂颗粒的模型参数如表3所示，测量圆的布局如图7所示。

①～为测量圆编号

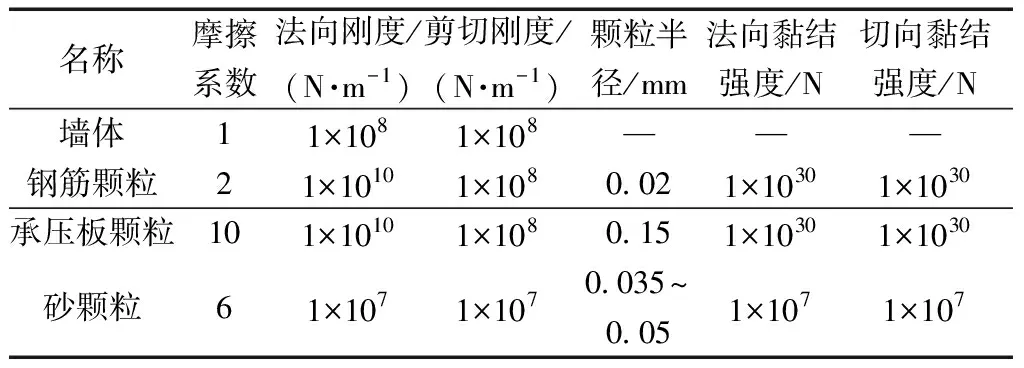
表3 锚固体系模型参数

2.2 数值模拟结果分析

2.2.1 压力型锚杆和压力分散型锚杆应力变化规律对比分析

图8为压力型锚杆和压力分散型锚杆模型周围土体的测量圆剪应力和轴向应力曲线。可以看出，压力型锚杆的锚固段处于受压状态，最大轴向应变出现在承压板周围，距离承载体越远，应变值越小；压力型锚杆的破坏模式为承载体周围锚固体的剪胀

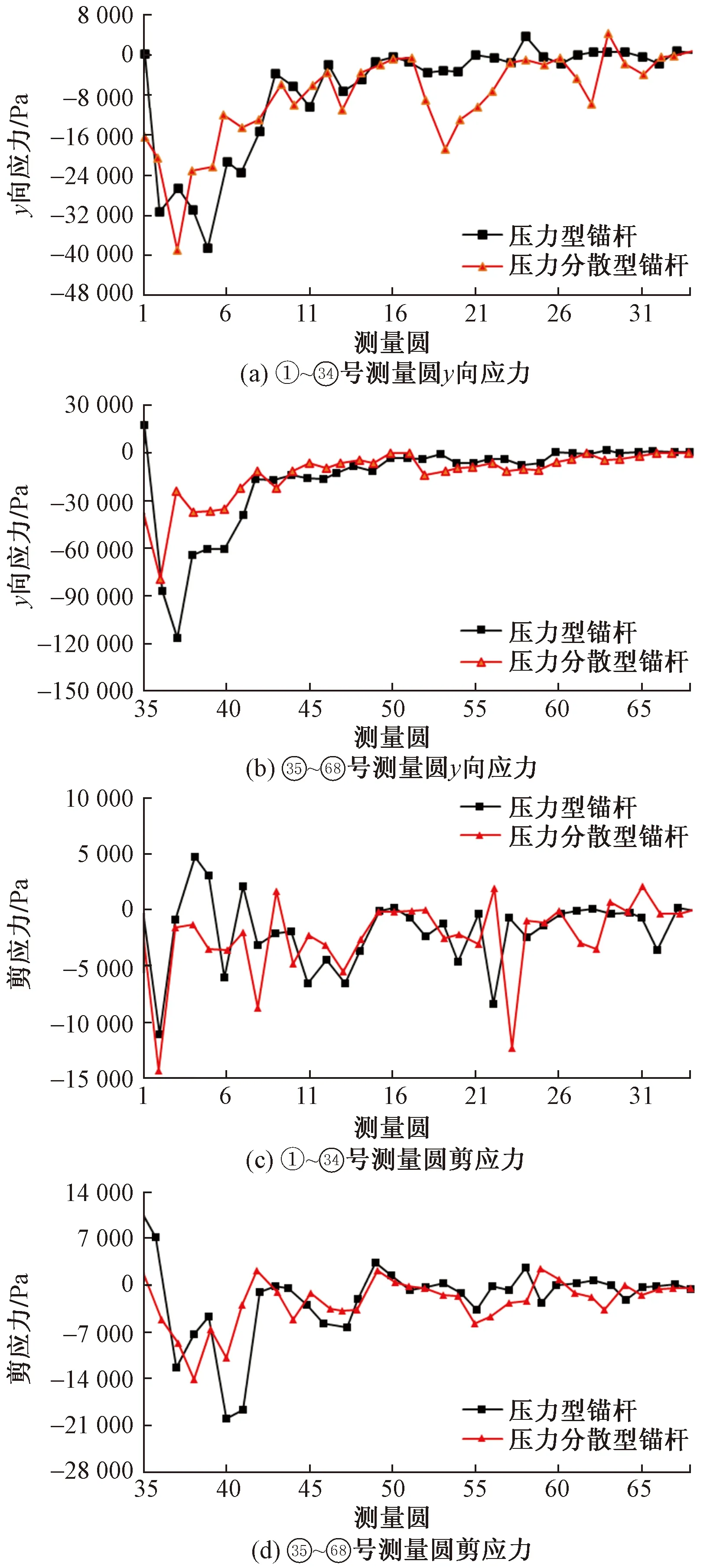
图8 轴向应力和剪应力变化曲线

破坏。压力分散锚杆周围土体应力分布均匀，波动小，峰值绝对值低。因此，与压力型锚杆相比，压力分散锚杆更稳定，不容易发生破坏。与压力型锚杆的界面剪应力在承载体附近有较高的应力集中相比，由于承压板的作用，压力分散锚杆的峰值剪应力大大降低，作用于两个承载体上，且在整个锚固长度上，剪应力分布更趋于均匀。

2.2.2 压力分散型锚杆细观参数平均值变化规律分析

将压力分散型锚杆锚固系统的数值模型分为4个层次，从左到右的每列测量圆分别对应于层次1～4。计算各层应力场、孔隙率、旋转量和颗粒配位数的平均值，观察不同参数的变化规律，揭示压力分散锚杆的细观锚固机理。模拟结果如图9(a)～图9(c)所示。

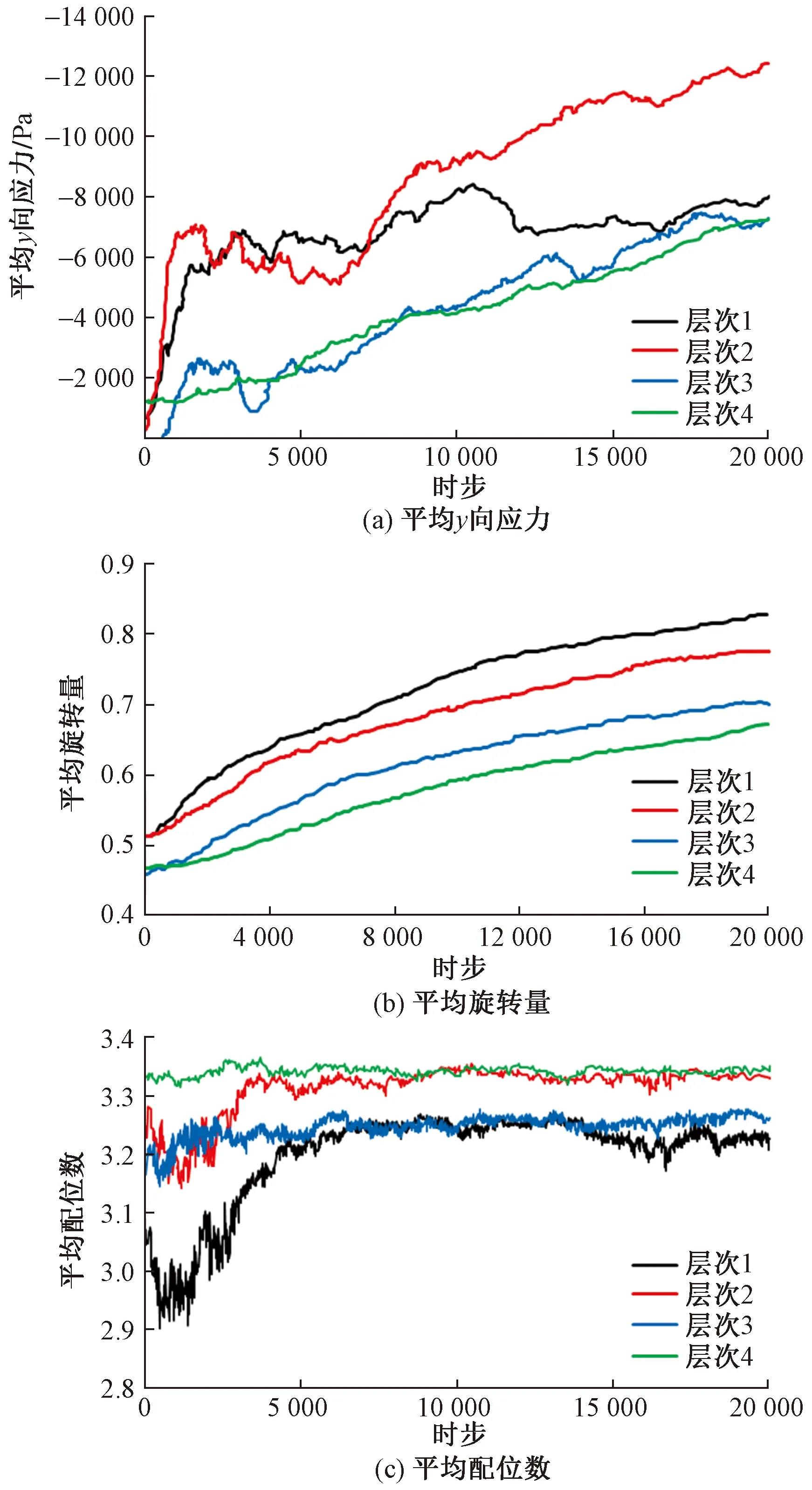
图9 平均细观参数随时步变化曲线

通过观察图9(a)可以看出，层次1在y方向上的最大和最小应力绝对值之间的波动最小，层次2～4的绝对值基本上呈现逐渐增加趋势，这4条曲线最终趋于稳定，表明由于承压板的存在，层次1成为杆体的延伸，其y向应力较小且逐渐稳定；层次2与注浆层相似，y向应力绝对值最大，受到的挤压最为强烈；层次3、4的y向应力绝对值随着离锚杆距离的增加而逐渐变小，这同外部荷载通过锚杆向周围土体外侧径向扩散且逐渐削弱的实际情况相吻合。从图9(b)可以看出，每层的平均旋转量先增加，然后趋于水平稳定，随着层次的增加，平均旋转量值减小，表明外荷载的影响随着时步的发展逐渐减小。通过观察图9(c)中的平均配位数曲线，层次1、2的曲线呈现反复减少和增加的趋势，层次3、4的曲线呈现逐渐增大，相同时步下，第1列数值最小，表明第1列相对最不稳定，第4列数值最大，表明离锚杆越远，平均配位数变化越小，受载荷动越小，其稳定性越好。

2.2.3 影响因素分析

砂土密度和锚杆埋深对砂土中锚杆的抗拔性能有很大的影响。基于颗粒流理论与PFC2D程序，考虑不同埋深、不同砂土密实度等影响因素，对压力分散型锚杆的受力性能进行数值模拟研究。

图10表明了锚杆埋深对y向应力和剪应力曲线的影响。在两种埋深下，结构的轴向应力和剪应力曲线呈现相同趋势，峰值的绝对值大小与锚杆埋深成反比，即锚杆埋深大的结构应力绝对值最小，表明应力更加均匀。数值分析结果与室内模型试验结果基本一致，在相同荷载下，锚杆埋深增加，锚杆的上拔承载力也相应的得到提高。

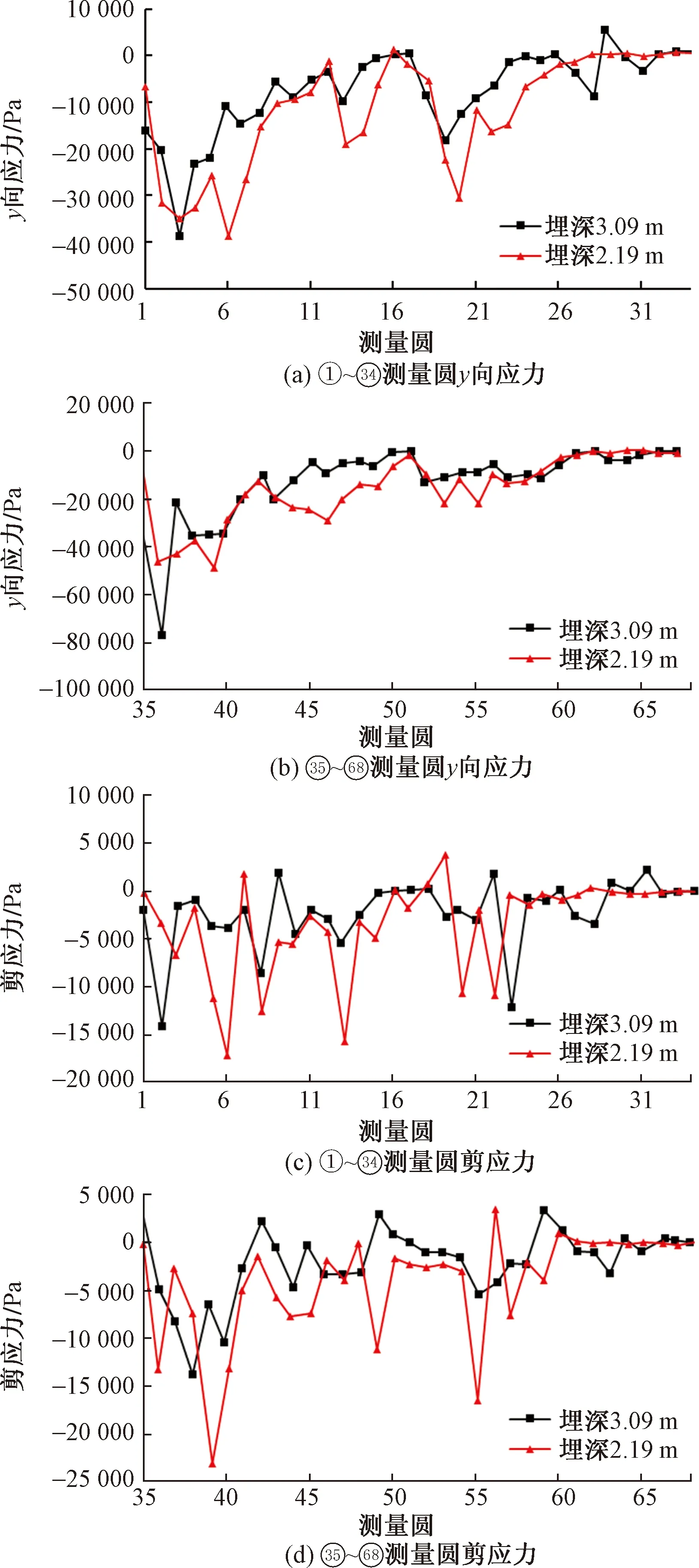
图10 不同埋深下轴向应力和剪应力变化曲线

从图11中可以看出，数值模拟结果与模型试验结果基本吻合，砂土密实度与y向应力和剪应力绝对值成正比，即随着砂土密实度的增加，在锚杆上拔过程中，由于周围土体的挤压作用更为强烈，尤其在承压板附近，因此锚杆越不容易被拔出，锚杆也就越稳定不易失效。

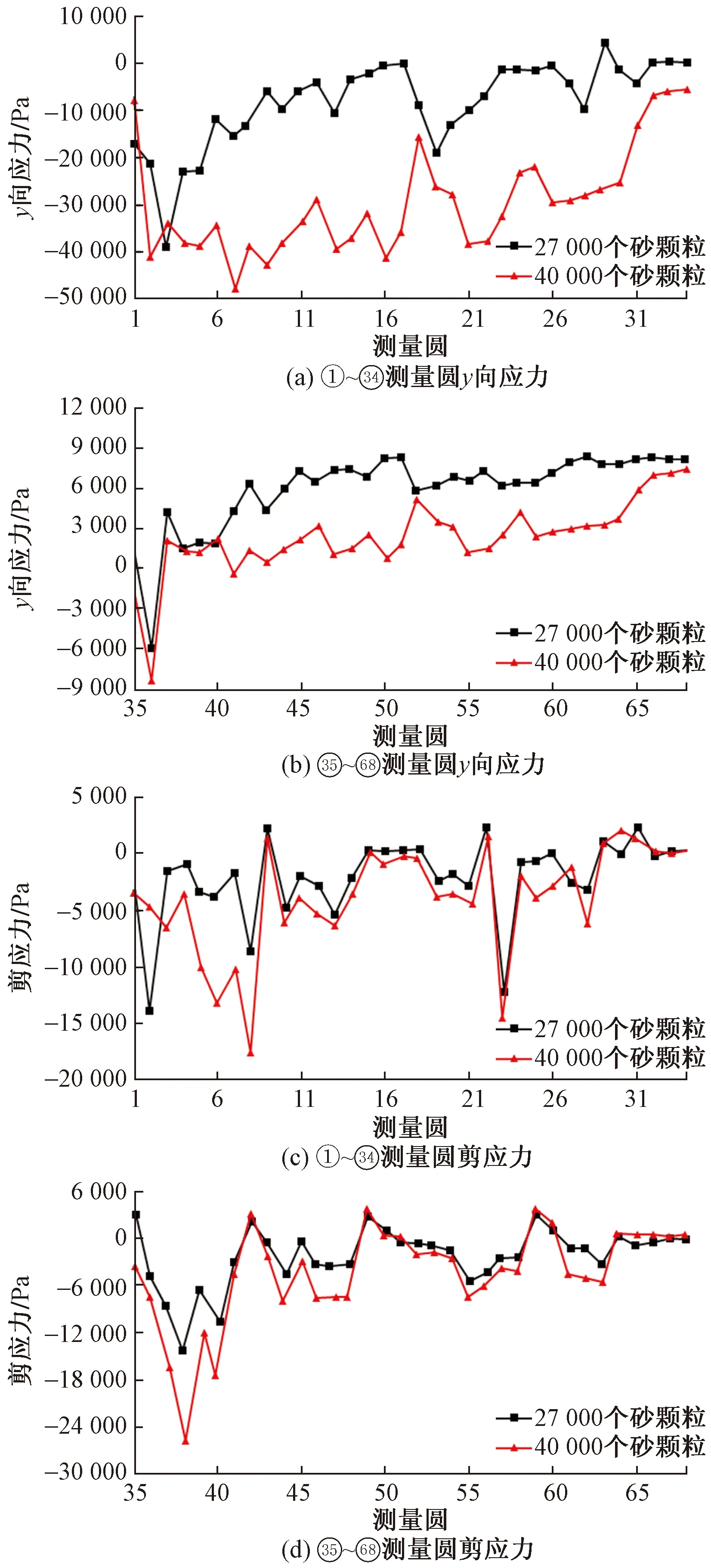
图11 不同砂土密实度下轴向应力和剪应力变化曲线

3 结论

结合室内试验及数值模拟，可以得出不同工况下压力分散型锚杆荷载-位移曲线及周围土体细观组构演化规律，得出如下结论。

(1)在相同埋深率和不同密实度下，松砂和密砂中锚杆的峰值上拔力差异很大，密砂中锚杆的峰值荷载约为松散中的两倍。对于峰值点的上拔位移，密砂和松砂之间也存在很大差异，松砂中锚杆达到峰值荷载的位移远大于密砂中的位移。

(2)对于埋置于松砂中的锚杆，不同埋深下杆周土体的破坏模式为冲切破坏，而埋置于密砂中的锚杆，不同锚杆埋深率下的杆周土体破坏模式不同。埋深率H/D=3的锚杆呈现扩展至土表面的梯形剪切面，埋深率H/D=6时，则为土体内部的局部破坏。

(3)随着锚片数量的增加，压力分散型锚杆的承载力增加。然而，当锚片数量的增加，使得锚片间的间距小到某一临界值时，增加锚片的数量将不会提高锚杆承载力。

(4)压力型锚杆的界面剪应力在承载体附近出现高度应力集中，压力分散型锚杆剪应力分布峰值为作用于两个承载体上，锚杆尾部承载体剪应力峰值大于另一个承载体处剪应力峰值。与压力型锚杆相比，由于承压板的作用，压力分散型锚杆的峰值剪应力大大降低，并且剪应力在整个锚固长度上趋于更均匀。

(5)砂土的密实度和锚杆埋深对锚杆在砂土中的抗拔性能有很大影响。增加砂土的密实度可以大大提高锚杆的抗拔承载力，显著减小锚杆的位移和变形，增加锚杆的埋置深度也可以大大提高锚杆的抗拔承载力。