混杂纤维混凝土抗压强度正交试验研究

吴海林，郭金雨，张玉

(三峡大学水利与环境学院，宜昌 443002)

混凝土作为水工建筑物的主要材料，在抗拉、抗折等方面的力学性能仍存在诸多不足，因此在混凝土中掺加纤维改善混凝土性能的研究[1-5]备受关注。研究表明，在水泥基材料中加入纤维，不仅可以抑制早期裂缝的产生，改善混凝土各方面力学性能如抗拉性能、弯曲韧性[6-7]和抗冲击性能等[8-9]，还可以改善混凝土结构的抗冻性[10-11]、抗渗性[12]以及抗腐蚀性[13-14]。近年来，在水电站压力管道结构的工程设计与实践领域，混杂纤维混凝土的应用受到越来越多学者的关注，混杂纤维混凝土为水电站压力管道结构裂缝控制问题的解决提供了另一种视角。

随着纤维混凝土应用的发展，纤维混凝土的种类越来越多，这些纤维都具有不同的尺寸、密度及弹性模量等参数，因此对于混杂纤维混凝土而言，纤维种类、纤维尺寸、纤维掺量等对混凝土性能的影响规律都需要进一步的研究。郑惟武等[15]对玄武岩、聚乙烯醇混杂纤维混凝土的抗压强度进行了研究，发现纤维种类和纤维尺寸是影响混凝土的抗压强度的关键因素；黄鑫等[16]研究表明，水灰比、砂率、纤维长度、水泥用量对混凝土抗压强度的影响依次变小；权长青等[17]研究发现，钢纤维和聚丙烯纤维体积分数对抗压强度有显著性影响，且钢纤维和聚丙烯纤维组合的混杂纤维混凝土力学性能表现出较好的混杂效果；Qian等[18]研究了不同尺寸钢纤维和聚丙烯纤维混杂后对抗压、抗折等力学性能的影响，得出结论短纤维可以提高混凝土的抗压强度。可见，混杂纤维混凝土的抗压强度不仅受混凝土配合比中各因素的影响，还受纤维的尺寸、混杂纤维的种类、各种纤维掺量等因素的影响。

通过调研发现，现有的相关研究成果大多以某一种确定的混杂纤维混凝土为研究对象，难以横向对比不同的纤维种类、纤维尺寸和纤维掺量等对混凝土的力学性能影响程度的差异性。为此，基于混杂纤维混凝土在水电站压力管道结构中的应用背景，设计正交试验，研究在同一基体混凝土强度下，纤维种类、纤维尺寸和纤维掺量对混杂纤维混凝土抗压强度的影响规律，并基于灰色系统理论建立混杂纤维混凝土抗压强度预测模型。

1 试验概况

1.1 原材料

鉴于水电站钢衬钢筋混凝土压力管道外包混凝土的强度等级以C25最为常用，并且现有的研究成果已表明：钢纤维与其他纤维的混掺组合对于钢衬钢筋混凝土压力管道外包混凝土的裂缝控制效果更为有利[19-22]，因此，在试验研究中将基体混凝土强度等级确定为C25，并且主要考虑钢纤维与其他种类纤维混掺的混杂纤维混凝土为研究对象。

试验材料如下：①水泥：宜昌三峡牌P·O42.5普通硅酸盐水泥；②粗骨料：连续级配、粒径5～40 mm的碎石；③细骨料：优质河砂，细度模数2.5；④水：实验室自来水；⑤减水剂：固含量为40%的聚羧酸母液；⑥纤维：分别选用宜兴市华源金属纤维有限公司生产的剪切波纹型钢纤维、石家庄市瑞鑫纤维素有限公司生产的束状单丝型聚丙烯纤维、浙江海宁市海宁安捷复合材料有限公司生产的短切玄武岩纤维以及中山纳丝新材料有限公司生产的纳米纤化纤维素纤维，纤维的具体参数如表1所示。

1.2 配合比设计

根据《钢纤维混凝土》(JG/T 472—2015)[23]和《普通混凝土配合比设计规程》(JGJ 55—2011)[24]计算得到本试验配合比如表2所示。在混杂纤维混凝土研究中，普遍采用不同弹性模量的纤维种类进行组合，选择弹性模量与钢纤维差异明显的几种纤维进行组合设计，各纤维的特征参数如表1所示。依据《钢纤维混凝土》(JG/T 472—2015)[23]中的规定并结合文献[25]，一般浇筑钢纤维混凝土中，钢纤维长度范围为20～60 mm，长径比范围为30～80，如果纤维过长时，混凝土拌制过程中会导致纤维变形严重，加剧纤维结团的不利影响，对试验结果产生不利影响，因此选取钢纤维长度范围20～35 mm进行尺寸设计；钢纤维常用掺量一般为0.35%～1.50%，不宜超过2%；根据《纤维混凝土结构技术规程》(CECS 38—2004)[26]，合成纤维的掺量宜在0.05%～0.30%范围内选取，也可根据工程要求通过试验和已有工程确定掺量。通过调研发现，当合成纤维掺量较大时纤维间会产生结团现象，如聚丙烯纤维掺量大于0.2%时，黏聚力会有突然降低，对试验结果会产生不利影响[27-28]。因此参照上述合成纤维常用掺量范围，确定聚丙烯纤维的试验掺量为0.05%～0.20%。关于玄武岩纤维和纳米纤维素纤维，目前相关的规范中并没有建议常用的掺量范围，文献[29-30]对掺量为0～0.3%玄武岩纤维混凝土进行了研究，建议玄武岩纤维的最优掺量为0.10%；文献[31]对掺量为0～0.4%纳米纤维素纤维混凝土进行了研究，结论建议较优掺量为0.10%。参照文献[32-34]的设计方法，综合考虑正交试验设计，将本试验中的玄武岩纤维、纤维素纤维的掺量范围同样确定为0.05%～0.20%。

表1 纤维的特征参数

表2 混杂纤维混凝土配合比(不含纤维掺量)

本试验涉及多个变量对抗压强度影响规律的研究，结合其他同类型研究中的分析方法[16,32-33]，可以选择正交的思想来设计试验方案。试验为研究纤维种类、纤维尺寸和纤维掺量对混杂纤维混凝土抗压强度的影响规律，考虑的因素及水平为：①混杂纤维组合(钢-聚丙烯、钢-玄武岩、钢-纤维素)；②钢纤维长度(20、25、30、35 mm)；③钢纤维掺量(0.5%、1.0%、1.5%)；4)聚丙烯纤维、玄武岩纤维和纤维素纤维的掺量(0.05%、0.10%、0.15%、0.20%)。

根据本试验的因素和水平数量，使用L16(43)的标准正交表，并采用拟水平法对正交表进行改造，共设计了17组试件，各试件主要参数如表3所示。

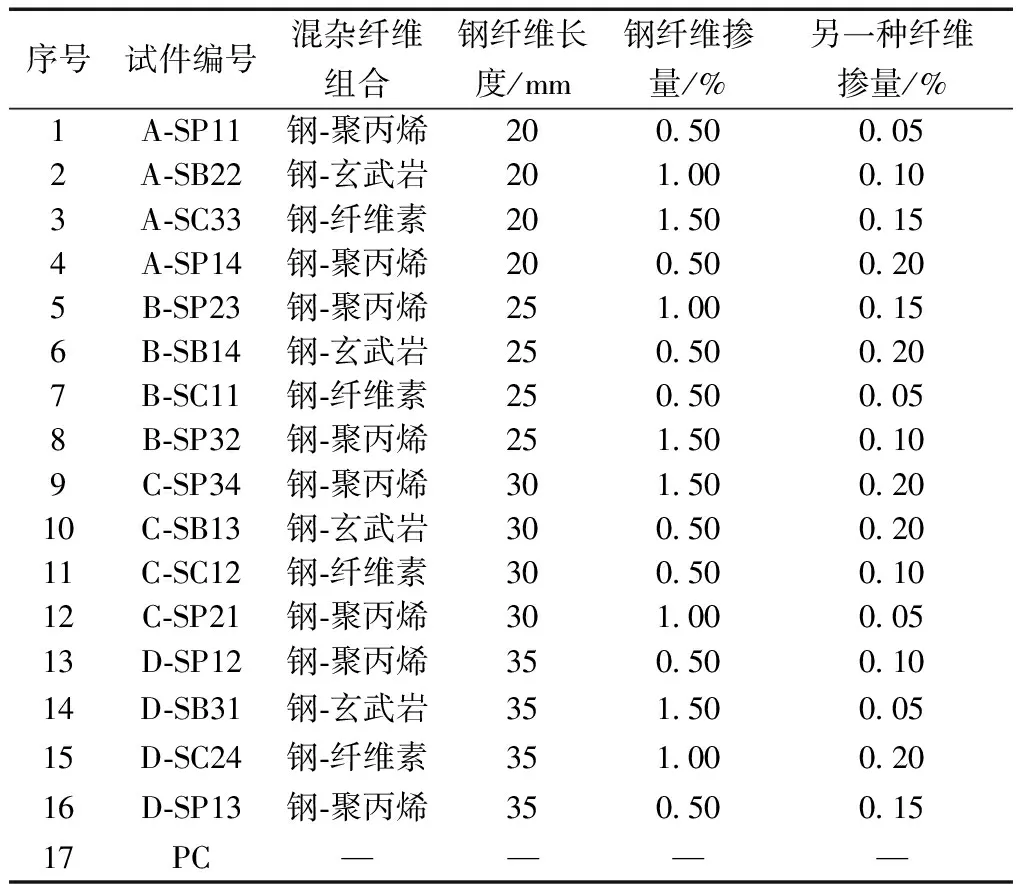
表3 试件主要参数

1.3 试件制备和试验方法

试拌过程中发现两种纤维的投放顺序对拌合物的搅拌质量影响较大，并且会产生纤维结团的问题。经过文献调研和多次的试验后，本试验采用干拌法，将两种纤维分开投放，可以很大程度上减少纤维结团的发生。每组配制150 mm×150 mm×150 mm的立方体试块3个。试件在标准养护室养护28 d后，从养护室取出，晾干。使用2 000 kN电液伺服万能试验机对试块进行抗压试验，以0.3～0.5 MPa/s的速度连续、均匀地加载，当试件接近失效并开始快速变形时，停止调节阀门，直至试件破坏，记录试件的失效荷载，立方体的抗压强度由3个试件的平均值确定。

2 试验分析

2.1 试验现象

素混凝土试件加载时，达到峰值应力后，试件快速破坏，混凝土与承压面垂直的表面崩碎掉落并伴随较大的爆裂声，立方体试件呈对顶锥面的破坏形式，如图1(a)所示。相比于素混凝土，混杂纤维混凝土试件在加载时，达到峰值应力后，表面会出现较多裂缝和脱皮现象，随着加载过程继续，试件表面裂纹增多，表面脱落碎块增多并伴随较小的爆裂声，试件整体完整性较好，破坏时间明显较长，如图1(b)所示。

图1 试件抗压破坏形态

2.2 试验结果分析

混杂纤维混凝土立方体试件和素混凝土立方体试件在标准条件下养护到28 d，对其进行抗压强度试验后，试验结果如表4所示。可以看出，抗压强度的变异系数均小于0.1，表明试验结果可靠；混杂纤维混凝土试件(除编号C-SC12试件)抗压强度均大于素混凝土，其中，D-SP12抗压强度最大，较素混凝土提高39.2%。

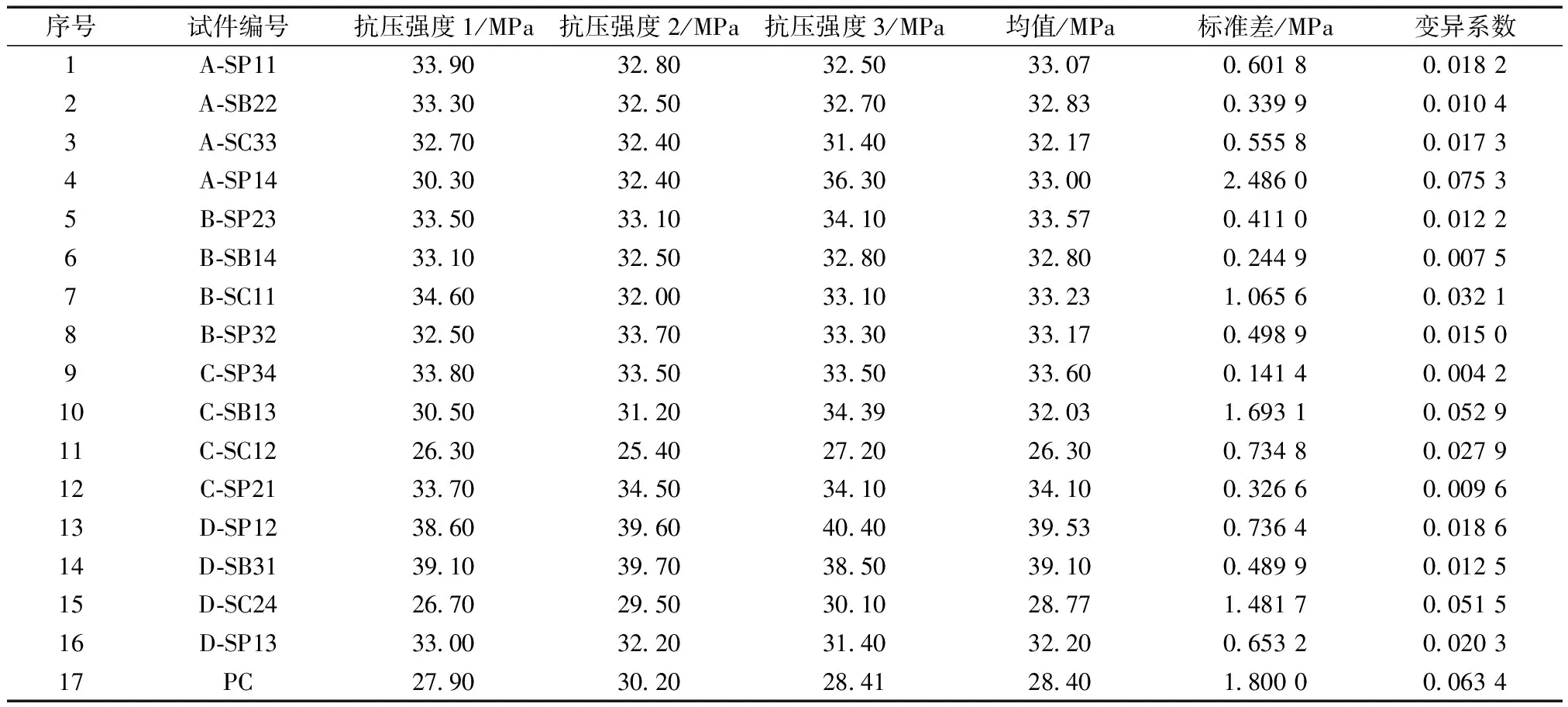
表4 立方体试件抗压试验结果

为了探究纤维种类、纤维尺寸和纤维掺量对抗压强度的影响程度，找出显著性影响因素，对抗压强度结果进行极差分析、方差分析和灰色关联分析。

2.2.1 极差分析和方差值分析

在极差分析和方差分析时，由于统计误差的存在和正交试验样本量少，影响程度较小的因素往往存在更大的误差，聚丙烯纤维、玄武岩纤维、纤维素纤维掺量只有0.05%～0.20%，对抗压强度的影响明显要小得多。因此在极差分析和方差分析中，用“混杂纤维组合”“钢纤维长度”“钢纤维掺量”分别代表“纤维种类”“纤维尺寸”“纤维掺量”进行分析。

在极差分析中，数据中极差值越大，说明该因素对于抗压强度的影响越大，从表5可以看出，纤维种类对抗压强度的影响程度最大，极差值为4.07 MPa；纤维尺寸其次，极差值为3.39 MPa；纤维掺量对抗压强度的影响最小，极差值为2.19 MPa。因此，3种因素对混杂纤维混凝土抗压强度的影响程度由强到弱依次为：纤维种类、纤维尺寸、钢纤维掺量。由表5可知，抗压强度最优的试件各因素组合应为钢纤维长度为3 mm、掺量为1.5%的钢-玄武岩混杂纤维混凝土。

在极差值分析中，数据中出现的统计误差容易对结果产生较大影响，因此需要借助SPSS进一步对结果进行方差分析，确定各影响因素的显著性。表6中，纤维种类和纤维尺寸的显著性水平P小于0.05，表现出对抗压强度具有显著影响；而钢纤维尺寸的显著性水平也表现出对抗压强度有一定的影响。因此，对于混杂纤维混凝土的抗压强度，各因素对抗压强度的影响程度由强到弱依次为：纤维种类、纤维尺寸、钢纤维掺量，这与极差分析结果一致。由此，纤维种类和纤维尺寸是影响混杂纤维混凝土抗压强度的重要因素。将极差分析和方差分析结果分别列于表5和表6。

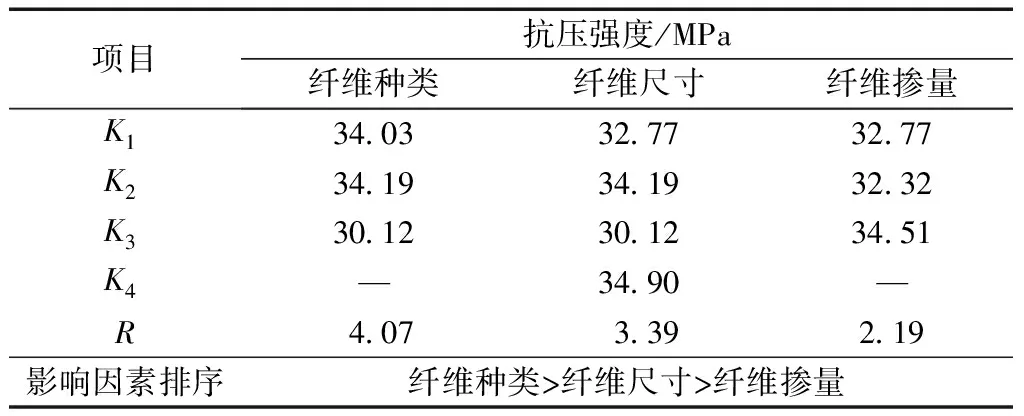
表5 混杂纤维混凝土抗压强度极差分析结果

表6 混杂纤维混凝土抗压强度方差分析结果

2.2.2 灰色关联分析

在试验数据有限和人为误差的影响下，许多数据并不能呈现明显的分布规律。灰色关联分析方法可以弥补数理统计分析中的缺陷，对样本量和样本规律性都没有要求。灰色关联分析基本思想是根据序列曲线几何形状的相似程度来判断不同序列之间的联系是否紧密[34]。为了准确地判断出各因素间的关联性，采用下列方法对关联度大小进行衡量。

确定抗压强度值为系统行为序列X0，纤维种类、纤维尺寸、钢纤维掺量和其他纤维掺量分别为相关因素序列(X1、X2、X3、X4)。在对纤维种类进行分析时，需要先对其进行量化处理，选择的不同纤维种类的主要区别是不同纤维的弹性模量(具体数据如表1所示)，因此将混杂纤维混凝土中聚丙烯纤维、玄武岩纤维、纤维素纤维与钢纤维弹性模量的比作为纤维种类的数据序列。由此，得到原始数据序列，如表7所示。

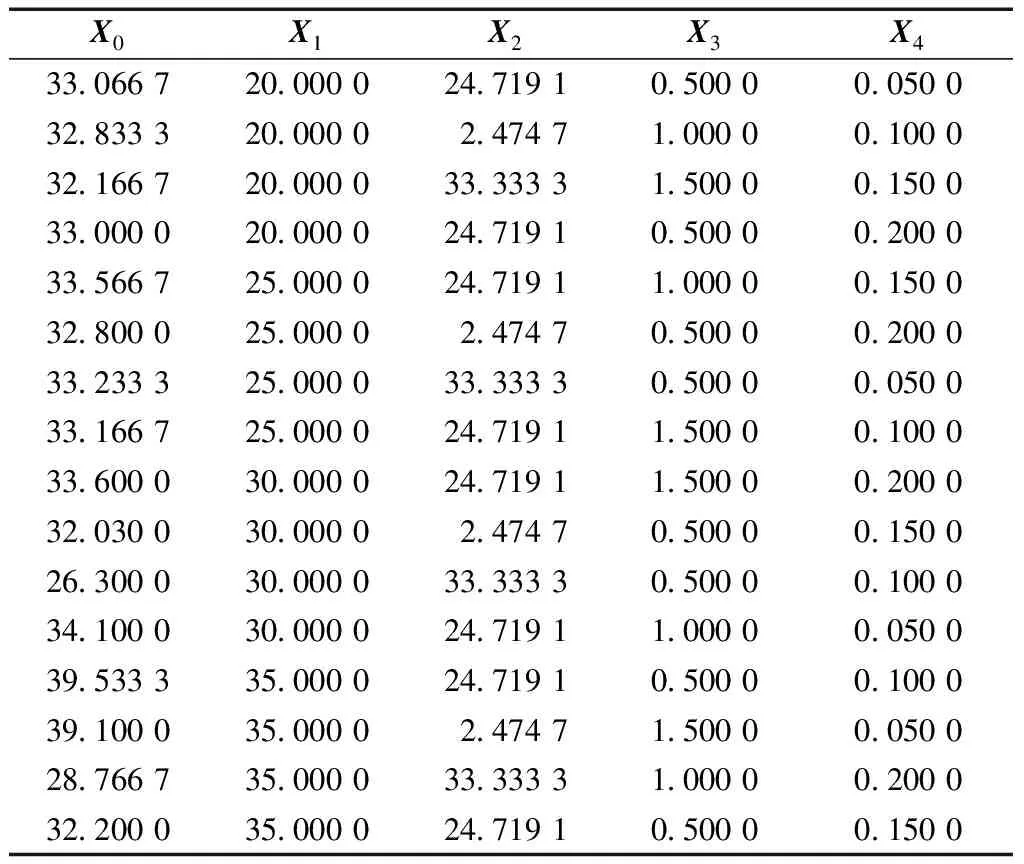
表7 混杂纤维混凝土抗压强度原始数据序列

为满足灰色关联计算时的公理化要求，首先要对所有数列进行初值化处理。按照式(1)～式(3)对原始序列进行初值变换，称数列D为序列算子，计算得到初值向量Y。

Xi=[x(1),x(2),…,x(16)]

(1)

Yi=XiD=[x(1)d,x(2)d,…,x(16)d]

(2)

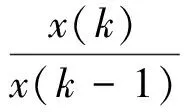
(3)

式中：纤维种类、纤维尺寸、钢纤维掺量和其他纤维掺量分别为相关因素序列Xi(X1,X2,X3,X4)；x(1)，x(2)，…，x(16)为16组试件关于Xi的原始序列；Yi为Xi初值化处理后得到的初值向量；D为序列算子；d为序列算子的元素，其中x(1)d=1；k-1表示1～16组试件的编号。

将初值向量Y代入式(4)中建立相关因素序列Yi和系统特征行为序列Y0的关联系数矩阵Z，ξ∈[0,1]为关联系数。通常情况下，关联系数越大，关联度越大，反之则越小。

Penfolds白葡萄酒家族在全球市场所受关注度逐年提升，Penfolds酿酒团队的匠心独具更是使新年份的白葡萄酒焕出新生。精选BINA霞多丽已发展成为一款独具特色的单一产区葡萄酒，富有现代风格与阿德莱德山区霞多丽的特征。

Zi=[γi(1),γi(2),…,γi(16)],i=1,2,3,4

(4)

(5)

式中：Zi为关联系数矩阵，即表8所示的矩阵；γi为关联系数矩阵的每一列矩阵；x0为抗压强度值的系统行为序列元素；xi分别为纤维种类、纤维尺寸、钢纤维掺量和其他纤维掺量分别为相关因素序列元素。

式(4)中表示某一固定时刻的关联系数，求出关联系数的平均值即为所要的关联度。将关联系数矩阵Z(表8)代入式(5)进行计算，得到相关因素序列Yi与系统特征行为序列Y0的关联度(表9)。

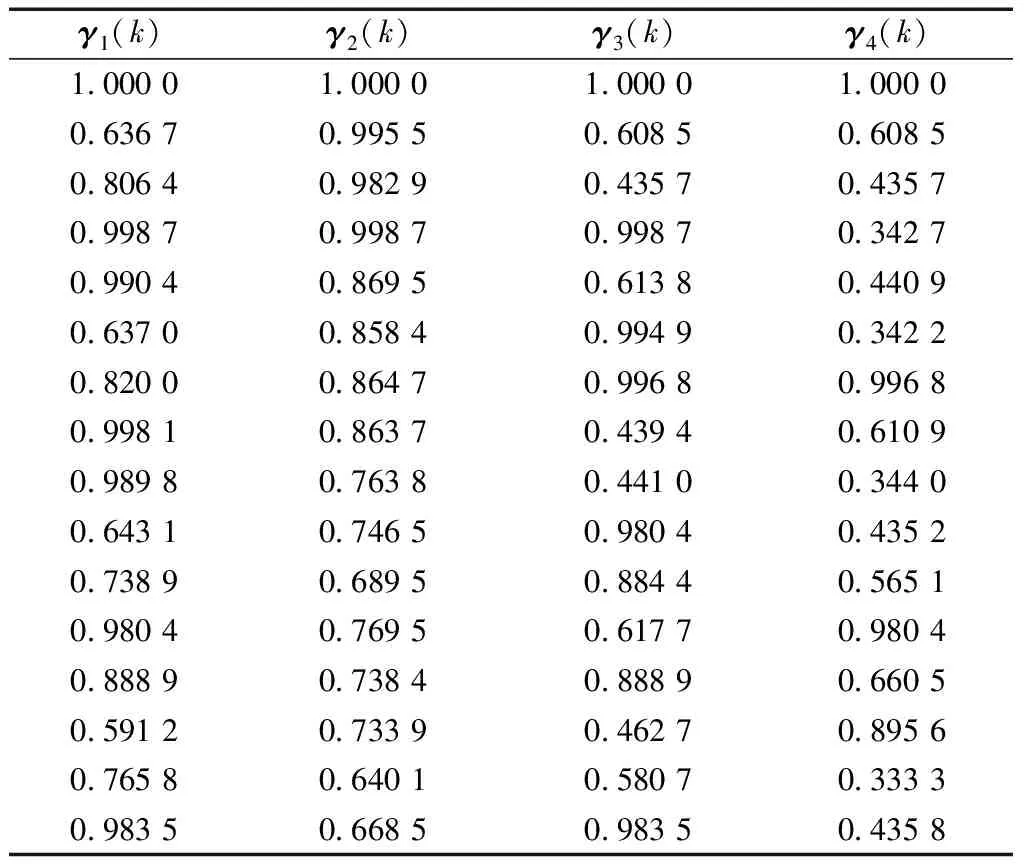
表8 混杂纤维混凝土抗压强度关联系数矩阵

表9 混杂纤维混凝土抗压强度灰色关联度

(6)

分析表9可知，关联度由大到小依次为：纤维种类、纤维尺寸、钢纤维掺量、其他纤维掺量。分析关联度的大小关系可以得出各因素的影响程度影响程度由强到弱依次为：纤维种类、纤维尺寸、钢纤维掺量，结果与方差值分析结果一致。

3 模型的建立与检测

传统的基于概率统计的预测模型通常需要大样本、服从典型分布等要求。根据灰色系统理论可知，GM(1,1)预测模型可以根据少量数据建模，通过序列算子的作用挖掘规律。灰色系统理论要求GM(1,1)预测模型需要建立在序列满足光滑或准光滑条件的基础之上。为了提高模型的精度，通常需要对原始序列进行预处理，提高序列的光滑性。光滑性越好，预测模型的精度也就越高。

3.1 GM(1,n)预测模型

考虑有5个变量，因此需要建立多变量灰色模型GM(1,5)。多变量灰色模型GM(1,n)不是GM(1,1)的简单组合，而是对GM(1,1)模型在n元变量下的拓广。对于多变量灰色模型GM(1,5)的建模步骤，大体遵循了GM(1,1)的建模步骤。

建立GM模型时，首先就是要构建原始数据序列，对于原始数据序列要想满足建模需求就要让原始数据满足光滑性或准光滑性的原则。判定原始数据是否光滑的充要条件是：∀ε>0,∃k0,当k>k0时，ρ(k)<ε，其中，ε为常数，k0为试验组数编号。

(7)

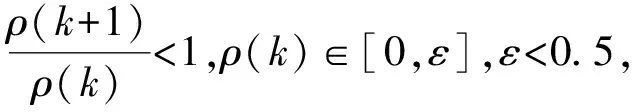
经检验，需要对原始序列进行式(8)的数-幂函数复合算子变换，同时为了保证变换后结果的整齐性，需要先对相关因素序列进行式(9)的序列算子变换，得到变换后的原始序列X(0)如表10所示。

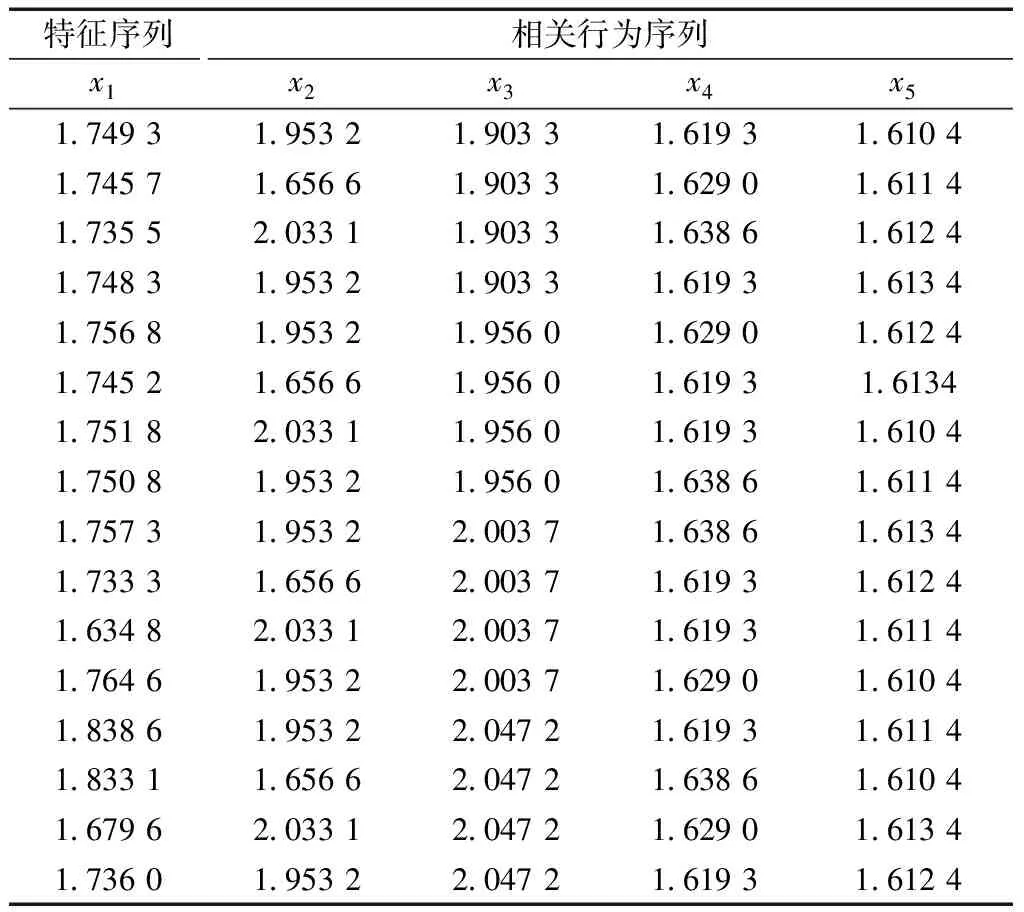
表10 GM(1,n)原始序列X(0)

x(k)d=lnx(k)1/2

(8)

x(k)d=x(k)+25

(9)

采用GM(1,5)建立混杂纤维混凝土抗压强度的灰色预测模型为

(10)

式(10)中：x1、x2、x3、x4、x5分别为混杂纤维混凝土抗压强度、纤维种类、钢纤维长度、钢纤维掺量、其他纤维掺量；a为系统发展系数；b1、b2、b3、b4为驱动项系数。

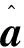
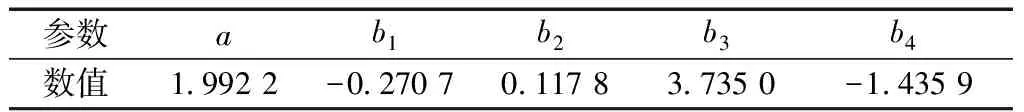
表11 GM(1,5)模型参数

(11)

式(11)中：l为试验的试件组数。

B=

(12)

(13)

(14)

(15)

得到抗压强度估计模型为

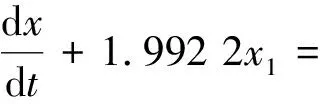
(16)

将结果转变为抗压强度预测模型标准式为

x(t-1)=-0.135 9x2+0.059 1x3+1.874 8x4-

0.720 8b4x5-(-0.135 9x2+

0.059 1x3+1.874 8x4-

0.720 8b4x5-1.749 3)e-1.992 2

(17)

式中：x1、x2、x3、x4、x5分别为混杂纤维混凝土抗压强度预测值、纤维种类、钢纤维长度、钢纤维掺量、其他纤维掺量变换后的原始序列。

3.2 抗压强度试验值和模型预测值对比

用混杂纤维混凝土抗压强度预测模型对16组混杂纤维混凝土试件进行预测和评价，并用残差检验的方法对结果进行检验，从而确认模型精度。抗压强度试验值和模型预测值对比结果如表12所示。用混杂纤维混凝土抗压强度预测模型对文献[36]中试件进行预测和评价，并对结果进行残差检验，将抗压强度试验值和模型预测值对比结果如表13所示。

表12 试件抗压强度试验值和模型预测值对比

由于在试验过程中立方体试件的抗压强度存在一定的离散性，在表12中个别试件抗压强度试验值与模型预测值的相对误差较大。但综合来看，这16组立方体试件的平均相对误差为7.08%，表明模型的预测效果良好。由表13可以看出，使用本文模型对文献[36]中试件的抗压强度进行预测时，除第4组试件外，其余相对误差都在10%以内，预测模型具有较高的预测精度。在表13中，第4组试件的相对误差偏大，分析其主要原因可能是其聚丙烯纤维掺量超出了本文选取的聚丙烯纤维掺量范围，但总体来看预测效果较好。

表13 文献[36]中试件抗压强度试验值与模型预测值对比

4 结论

通过设计正交试验，研究混杂纤维混凝土的纤维种类、纤维尺寸、纤维掺量3种因素对其抗压强度的影响，结合正交试验的极差值分析、方差值分析以及灰色系统理论的相关方法对混凝土抗压强度结果进行分析与建模，得出如下结论。

(1)相较于素混凝土试件，混杂纤维混凝土试件的抗压破坏过程更长，相同破坏条件下试件的完整性更好，具有明显地破坏预兆。试验结果表明混杂纤维混凝土试件抗压强度明显大于素混凝土试件，其中D-SP12抗压强度最大，较素混凝土试件提高39.2%。

(2)对试件抗压强度进行极差值分析和方差值分析，可以得出各因素对抗压强度的影响程度由强到弱依次为：纤维种类、纤维尺寸、钢纤维掺量；灰色关联分析的结果亦与之一致，各因素对抗压强度的影响程度由强到弱依次为：纤维种类、纤维尺寸、钢纤维掺量、其他纤维掺量。

(3)建立混杂纤维混凝土抗压强度预测模型，根据试验值和预测值的相对误差进行检验，试件抗压强度的试验值与模型预测值的平均相对误差为7.08%，表明该模型的预测精度较高。