疲劳拉伸载荷作用下的表面裂纹扩展分析
庞闯, 田干*, 刘德俊, 郭一, 刘蒙蒙
(1.火箭军工程大学导弹工程学院,西安 710025;2.哈尔滨师范大学数学与统计学院,哈尔滨 160025)
贮箱是一种大型的薄壁容器,结构材料多为各类铝合金[1],在制造、安装或服役过程中会不可避免地产生裂纹缺陷、导致结构材料的承载服役能力下降,进而引起容器泄漏和断裂等失效事故。而应力强度因子是含裂纹缺陷结构完整性评价的主要断裂参量[2],因此,当前针对应力强度因子的计算以及变化规律的研究仍然广为关注,同时对于疲劳裂纹扩展以及寿命的分析机理的评判依旧处于不断更迭的过程中[3-5]。针对推进剂贮箱金属焊接件疲劳裂纹,赵颖等[6]通过仿真在应力强度值最大的危险区域引入裂纹,对不同角度和尺寸系数的裂纹对各类应力强度进行分析,得到各类强度因子随着裂纹扩展的变化规律;Berer等[7]分析了在压缩载荷下强度因子随裂纹形貌的变化规律,并计算出强度因子是有关裂纹长度和深度以及裂纹间距的函数;Zareei等[8]使用权函数法研究管道内表面半椭圆裂纹在长深比大于1的最深点应力强度因子变化,并计算出在裂纹面承受不同应力分布情况下的应力强度因子分布公式;余建星等[9]从裂纹深度、长度以及管道内压力区间3个方面得到了裂纹断裂参数对疲劳寿命的影响。
目前,尽管对裂纹的探究已经从裂纹形貌、裂纹面载荷以及裂纹夹角等角度对裂纹尖端断裂参量以及疲劳寿命进行了分析研究,但仍旧是以静态裂纹作为研究对象而非对动态裂纹扩展过程中的尖端断裂参量或疲劳寿命以及扩展过程中的机理和裂纹面形貌的形成进行详尽的分析与探讨,因此对动态裂纹的扩展机理的研究不仅能够填补断裂失效问题的空缺,更能够促进对含缺陷结构强度的评估。为此,通过Franc3D裂纹分析软件对在疲劳拉伸载荷作用下不同长深比的半椭圆裂纹的扩展机理以及疲劳寿命的计算进行了探讨与研究,不仅分析了疲劳裂纹扩展中动态应力强度因子的变化规律,还对裂纹扩展路径、速率以及寿命的计算等方面展开了深入研究,对贮箱铝合金的应用以及材料安全稳定性评价具有一定的工程价值。
1 应力强度因子计算
应力强度因子作为可以衡量裂纹尖端相关奇异场的断裂参量,KΙ、KⅡ、KⅢ为3种基本裂纹尖端处应力奇异点的强弱程度[10]。由线弹性断裂力学,其数值表征与裂纹尖端应力场和应变场存在以下关系[11-15]。
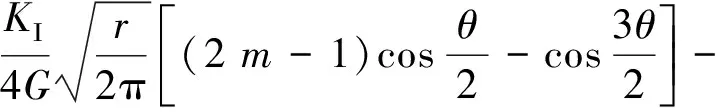
o(r)
(1)
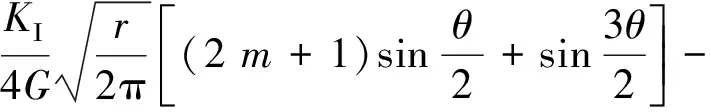
o(r)
(2)
(3)
式中:u、ν、ω为笛卡尔坐标系3个位移分量;m为常数;o(r)为高阶项;r、θ为极坐标系下尖端长度和角度;G为剪切模量,与材料相关。
当θ=±180°,可忽略高阶项o(r),得到的计算公式为
(4)
(5)
(6)
基于理论计算表达式,对于很多数值计算软件中关于应力强度因子的计算主要采用相互积分法、扩展有限元法以及M-积分法,而Franc3D通过M-积分对裂纹尖端应力强度因子计算,其表达式为[16-17]
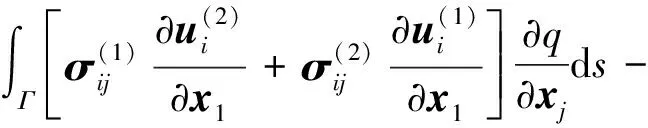
(7)
式(7)中:Γ为围绕裂纹尖端的积分回路;ui、xj、x1为位移分量;下标i、j为张量表示法;δ1j为i=1时的单位张量;s为单位维线长度;q为0与1的条件数值函数;应变能密度W(1,2)可表示为
(8)
式(8)中:σij、εij分别为应力和应变张量。
M-积分与应力强度因子关系为
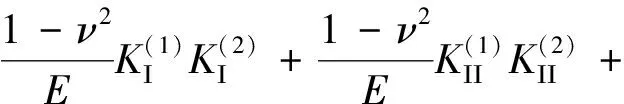
(9)
式(9)中:E、ν分别为弹性模量和泊松比。
工程中,大多数含裂纹结构断裂失效主要由张开型裂纹疲劳扩展引起的,因此对裂纹尖端断裂参量KI应作为主要研究对象进而探究疲劳裂纹扩展机理以及作为含裂纹体疲劳寿命的理论依据。
2 不同初始形貌下的疲劳裂纹扩展分析
2.1 有限元模型
对不同初始形貌下的疲劳裂纹扩展过程中的尖端动态应力强度因子的变化规律进行分析,以标准疲劳拉伸试样为研究对象,对含初始不同长深比c/a的半椭圆裂纹试样进行裂纹扩展仿真,设定裂纹长深比为小于1、等于1和大于1三种类型,即固定裂纹深度a为1 mm,材料表面裂纹长度2c分别为1.6、1.8、2.0、2.2、2.4 mm,同时,裂纹置于试样中心位置处,其试样尺寸以及相应的裂纹位置标注如图1所示,材料使用2 195-T8合金,其参数如表1所示。

表1 2 195-T8材料参数
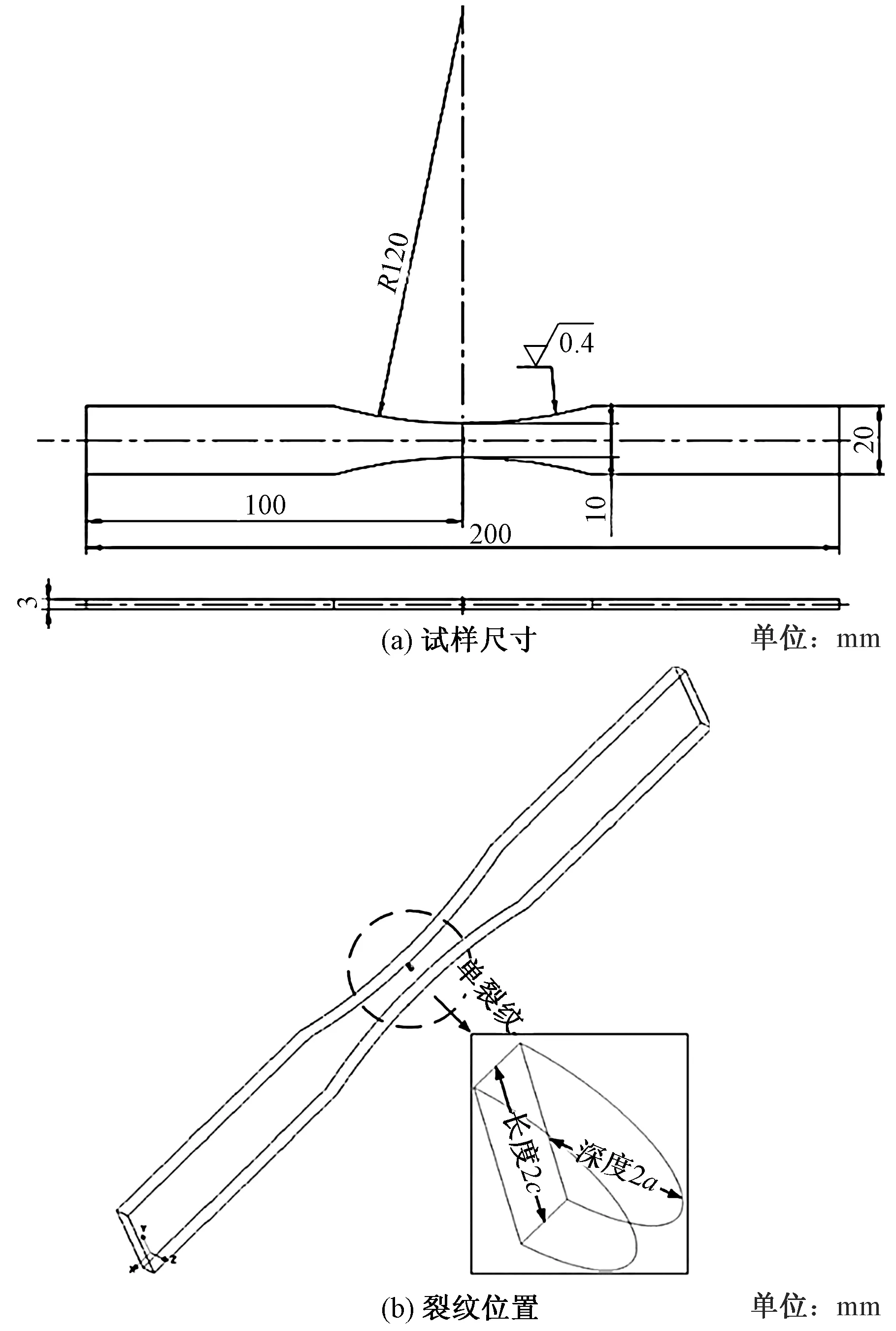
图1 试样尺寸与裂纹位置
按实际尺寸,在ANSYS环境中建立模型 并划分不含裂纹特征的试样网格模型,由于完整试样为均匀规则的连续体,因此采用扫略网格划分方法,并赋予网格类型为20节点的Solid186单元,单元数为10 200,节点数为50 255,其完整试样网格如图2所示。

图2 不含裂纹试样网格
由于Franc3D需导入ANSYS前处理文件,因此将完整网格模型导进Franc3D中,同时将各种不同初始长深比c/a的半椭圆裂纹插入至试样中心位置,此时因为裂纹的存在使得试样不再是完整的连续体,所以网格自动由六面体网格转化为自适应四面体网格从而能对裂纹特征更好地进行捕捉,含不同初始长深比c/a裂纹试样重分网格后的网格模型如图3所示。
由裂纹空间网格(图3)可知,整个试样网格与裂纹相接的部分都转换为四面体网格,同时裂纹网格由表面处过渡到尖端,其网格密度逐渐增加,同时在尖端边缘处网格为保证计算准确可行,因此采用映射面网格划分方法使得裂纹尖端处网格光顺平整化。

图3 不同长深比的裂纹网格
2.2 疲劳裂纹扩展分析
在ANSYS分析环境中设置其边界条件为一端固定,一端施加拉伸荷载为10 kN;再在Franc3D中设置其疲劳拉伸荷载的应力比R=0.1,即裂纹在1~10 kN的载荷范围内进行扩展,进而对含不同初始形貌裂纹的试样进行裂纹扩展的计算。
鉴于裂纹在疲劳拉伸载荷作用下进行扩展,因此采用分析环境当中的最大拉伸应力准则,即裂纹沿环向应力σθθ最大的方向进行扩展,而有关于σθθ的由第一类应力强度因子求解得
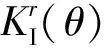
(10)
式(10)中:r为裂纹尖端半径长度。
同时通过指定裂纹扩展步长为10,将裂纹前缘中点处扩展距离为0.1 mm,进而对不同初始长深比c/a的半椭圆裂纹进行扩展分析在应力比R=0.1的疲劳拉伸载荷作用下,不同长深比下的初始半椭圆裂纹的尖端应力强度因子以及扩展过程的变化如图4所示。
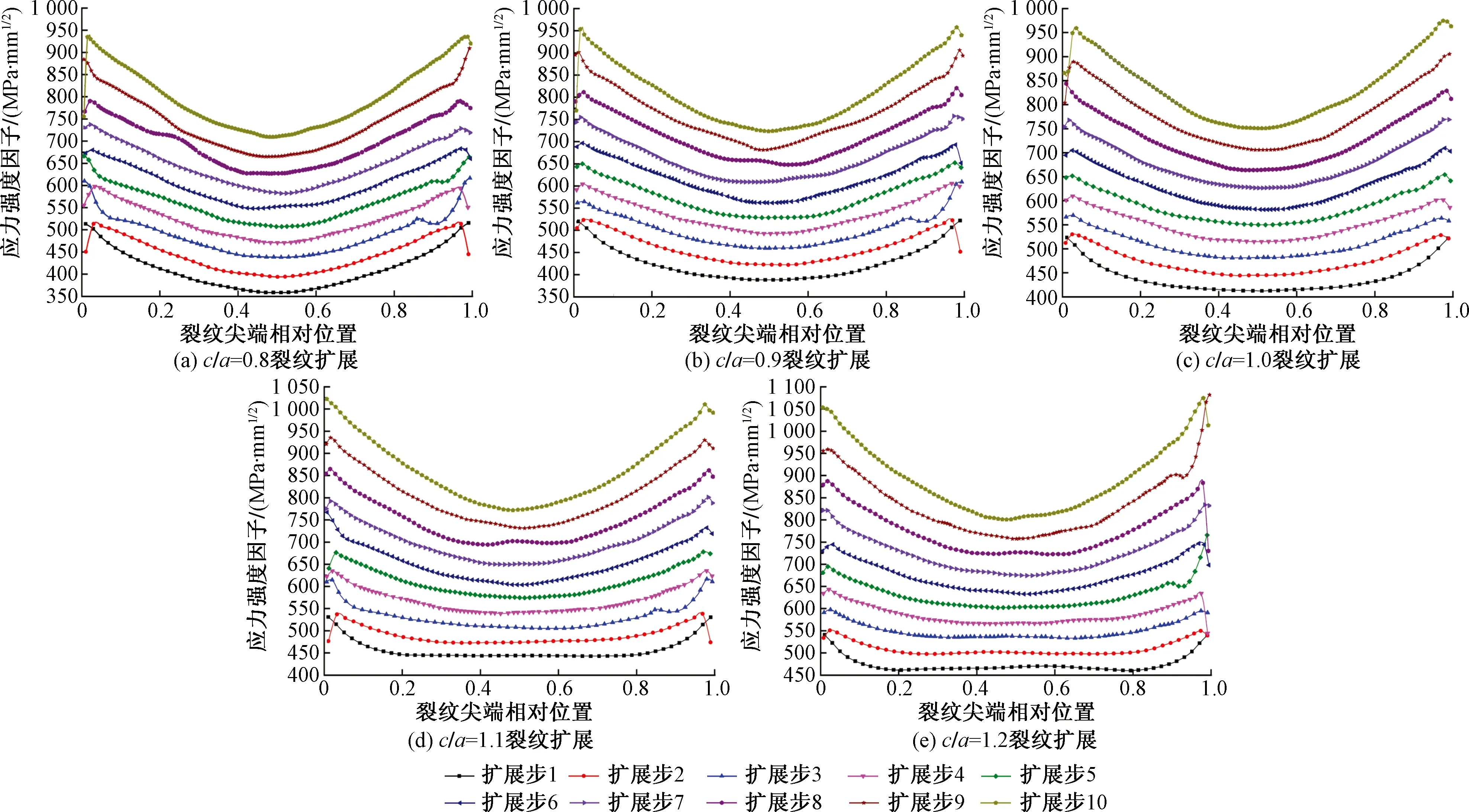
图4 不同长深比下的半椭圆裂纹扩展
图4反映了不同长深比c/a的半椭圆裂纹在疲劳拉伸载荷作用下扩展过程中的尖端应力强度因子的变化进程,其横坐标代表裂纹尖端各个计算节点与裂纹表面节点的距离与裂尖总长的比值,因此以裂纹尖端相对位置进行表征。由图知,总体上,裂纹在疲劳拉伸载荷作用下,裂纹在扩展中的尖端应力强度因子数值的变化比较均匀;同时,不论c/a小于1、等于1或大于1,其应力强度因子数值在裂纹靠近试样表面处的大小总是高于裂纹在深处方向的数值,因此不论哪一类长深比的半椭圆裂纹,其在材料表面即沿长度方向上的扩展要高于沿深度方向上的扩展程度。
另外,在裂纹刚扩展的阶段,其尖端表面点以及深度方向上的应力强度因子数值上的差值较小,但是在第6个扩展步之后其数值差异则改变的越来越大,说明裂纹在刚开始尖端向前扩展沿各个方向的扩展都比较均匀,但是随着扩展的进行其沿表面长度方向上的扩展已变成主导的扩展方向。从单条裂纹看,裂纹长深比的不同对初始裂纹尖端的应力强度因子分布有所影响,即沿深度方向上的尖端应力强度因子大小逐渐升高,而材料表面点上的数值大小相差不大但是总高于深度方向的数值大小,但对于扩展过程中的强度因子在数值上除了有所升高外,其在扩展中的尖端分布情况随着裂纹长深比c/a的增加所对应的变化并不明显。综上,工程实际中,对于不同深长比的疲劳裂纹扩展需要着重考虑其在表面处所引起的结构失效;另外,虽然对于不同深长比的疲劳裂纹其初始裂纹尖端的应力强度因子变化不一致,但是其扩展过程中的断裂参量的分布以及裂纹扩展趋势都很接近,因此可以针对此特点对疲劳载荷作用下的裂纹扩展进行统一评估与研究。不同长深比初始裂纹的扩展路径如图5所示。
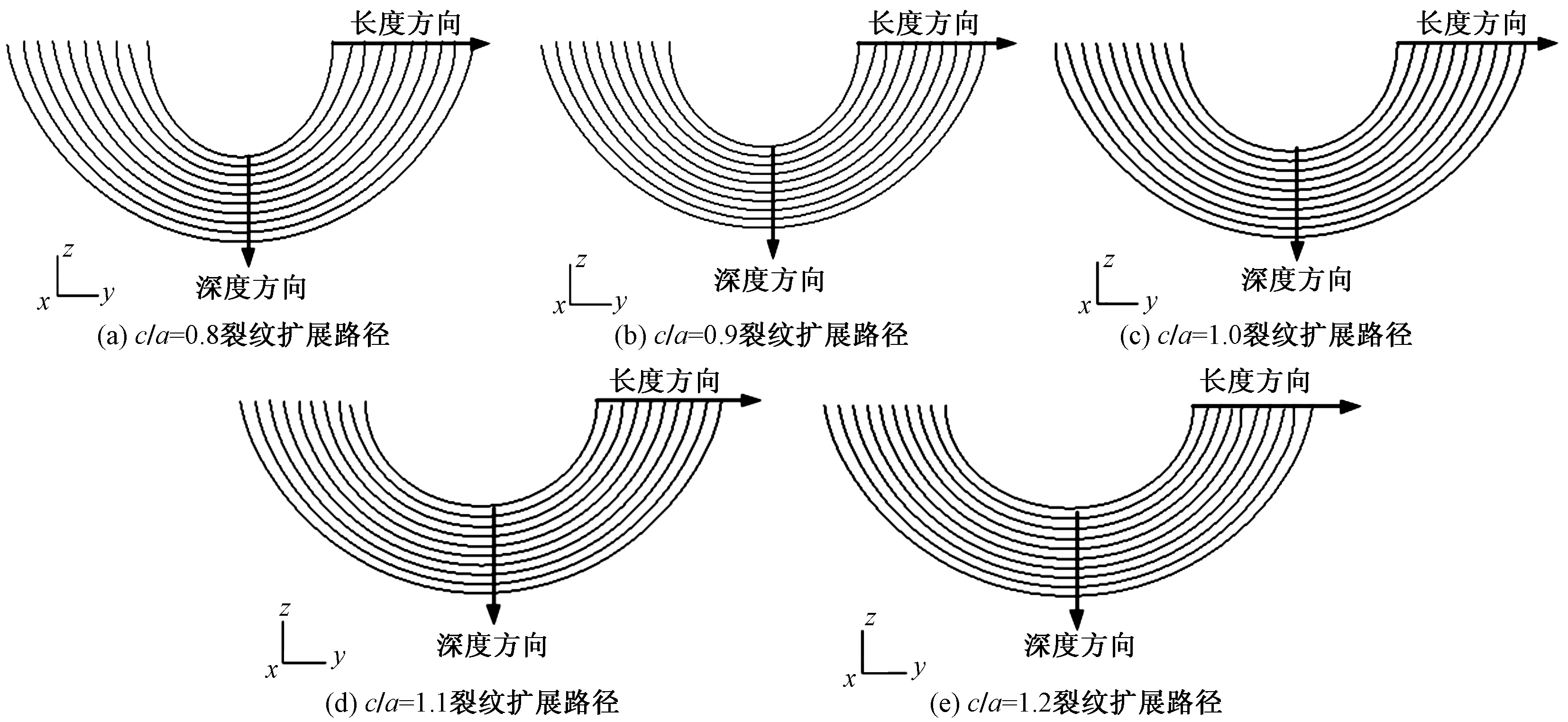
图5 不同长深比下的半椭圆裂纹扩展路径
可以看出,不同长深比c/a的疲劳裂纹的扩展进程比较均匀,其扩展距离从深度a方向到沿表面长度c方向由小至大变化,即裂纹沿深度方向扩展较慢而沿长度方向的扩展较快,从而使得不同初始长深比c/a疲劳裂纹随着扩展的进行,整体的裂纹形貌处于半椭圆形,因此从裂纹扩展路径上看,不论哪一类长深比的疲劳裂纹在拉伸疲劳载荷作用下会均匀扩展并且其裂纹的最终形貌仍旧为半椭圆形,且沿表面长度方向扩展的距离最长。
3 疲劳裂纹寿命分析
在上述裂纹扩展的基础上,需探究在相应裂纹扩展距离下的循环次数大小,因此从裂纹长度与深度方向两个角度比较不同长深比c/a初始裂纹在相同疲劳载荷下寿命变化规律,从而更好判断疲劳裂纹扩展的内在机理。
3.1 疲劳裂纹寿命理论
针对恒定幅值疲劳拉伸载荷下裂纹苦战规律,通常以Paris公式作为裂纹扩展速率公式为[17]
(11)
式(11)中:NP为应力循环次数;ΔK为应力强度因子变程;C和n为材料常数。
以Paris公式为依据,可以相对合理的判断出裂纹扩展寿命,裂纹由开始长度a0发展到最大裂纹长度ac所经受的应力循环次数为[18]
(12)
临界裂纹尺寸ac,其表达式为
(13)
式(13)中:KΙC为断裂韧度;σs为屈服强度;φ为第二类椭圆积分,有
(14)
即
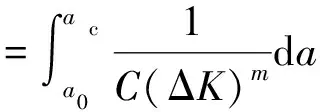
(15)
式(15)中:F为外部载荷;Δσ为应力幅值。
得
(15)
3.2 疲劳裂纹寿命仿真结果分析
根据在疲劳拉伸载荷下不同初始长深比的半椭圆裂纹扩展结果,通过在Franc3D设定疲劳寿命Paris模型,从而分析扩展中的裂纹寿命,其中材料参数C和n分别取为1.313×10-7和2.802[19],其扩展模型如图6所示。
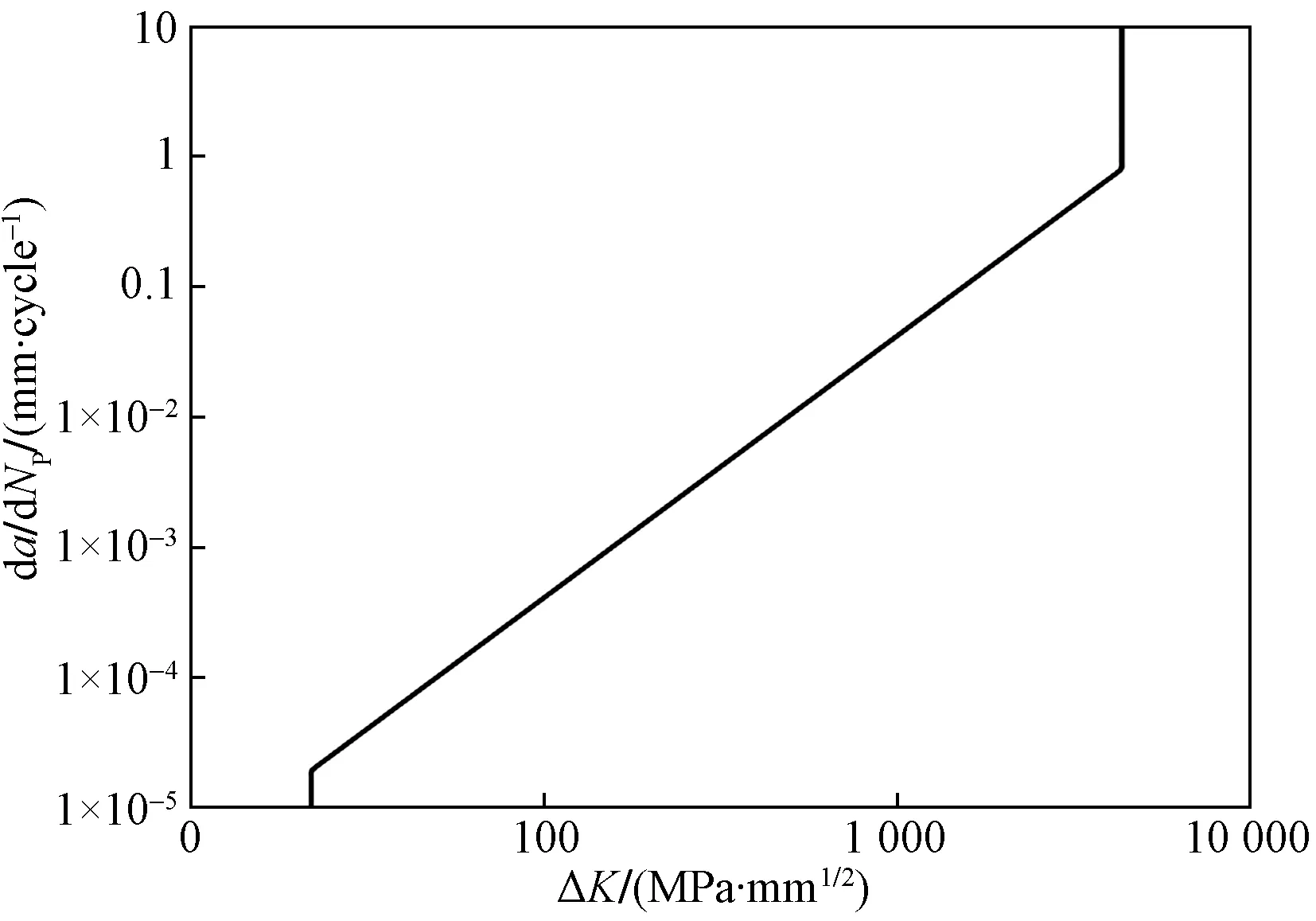
图6 2195-T8疲劳裂纹的da/dNP-ΔK曲线
不同初始长深比的半椭圆在疲劳拉伸载荷作用下其沿深度方向以及表面长度方向的扩展距离与疲劳寿命的曲线如图7所示。可以看出,对于不同长深比下的疲劳裂纹扩展寿命,在相同疲劳拉伸载荷作用下,其裂纹扩展距离与循环次数曲线的总体趋势十分相近,即疲劳裂纹扩展时其沿长度方向的扩展速率比沿深度方向上的速率更快,即在疲劳拉伸载荷下,含裂纹体主要由于裂纹在表面处扩展从而导致构件的断裂失效;而且不论沿长度或深度方向扩展,曲线斜率即裂纹扩展速率随着裂纹扩展的进行越来越高,因此不论哪一种长深比的裂纹需要在发现的初期采取相应的保护措施,否则越到裂纹扩展后期,压力管道越容易失效。
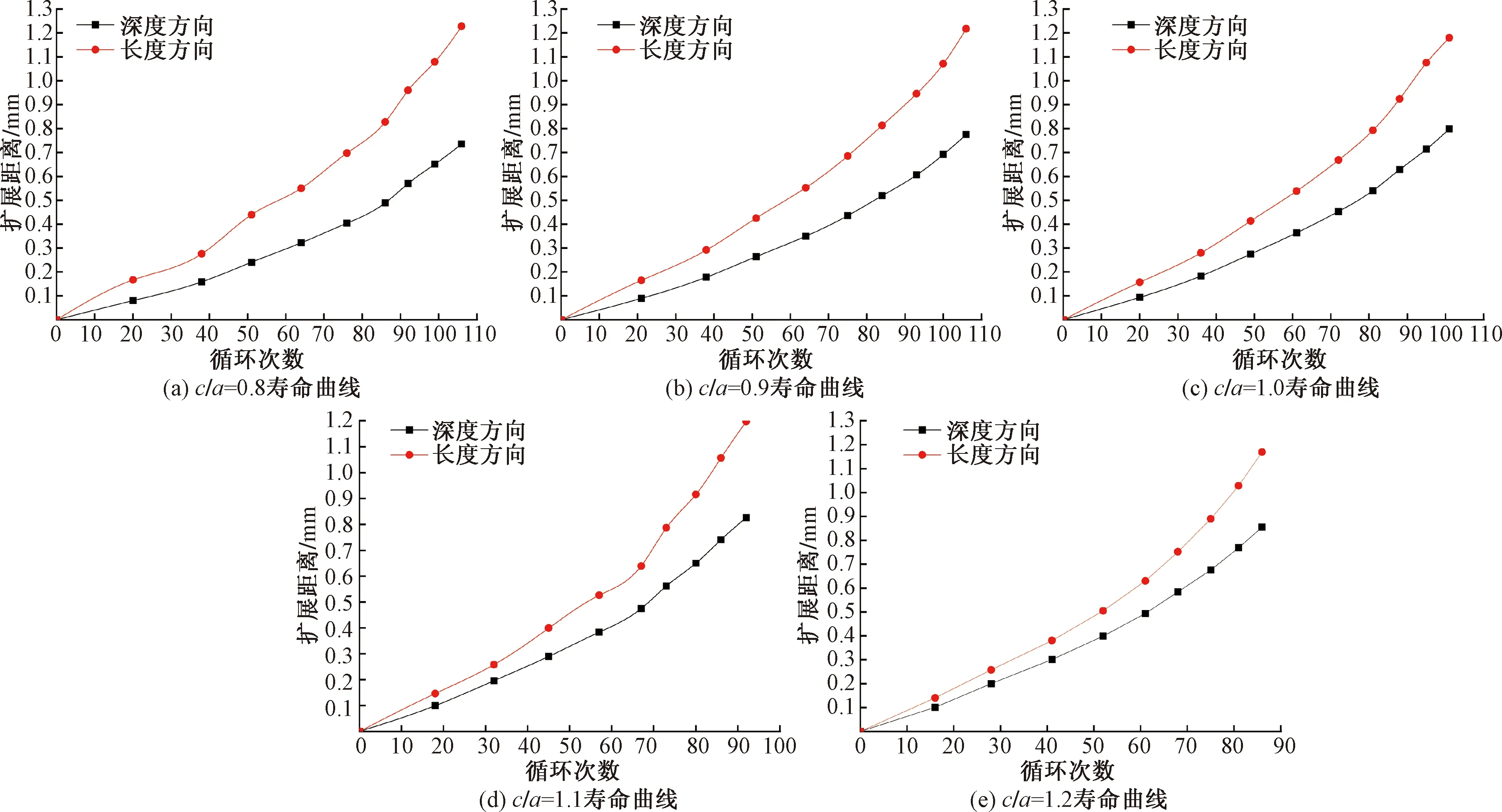
图7 不同长深比的疲劳裂纹寿命
5种长深比a/c疲劳裂纹沿深度或长度方向上扩展距离与循环次数的曲线如图8所示。
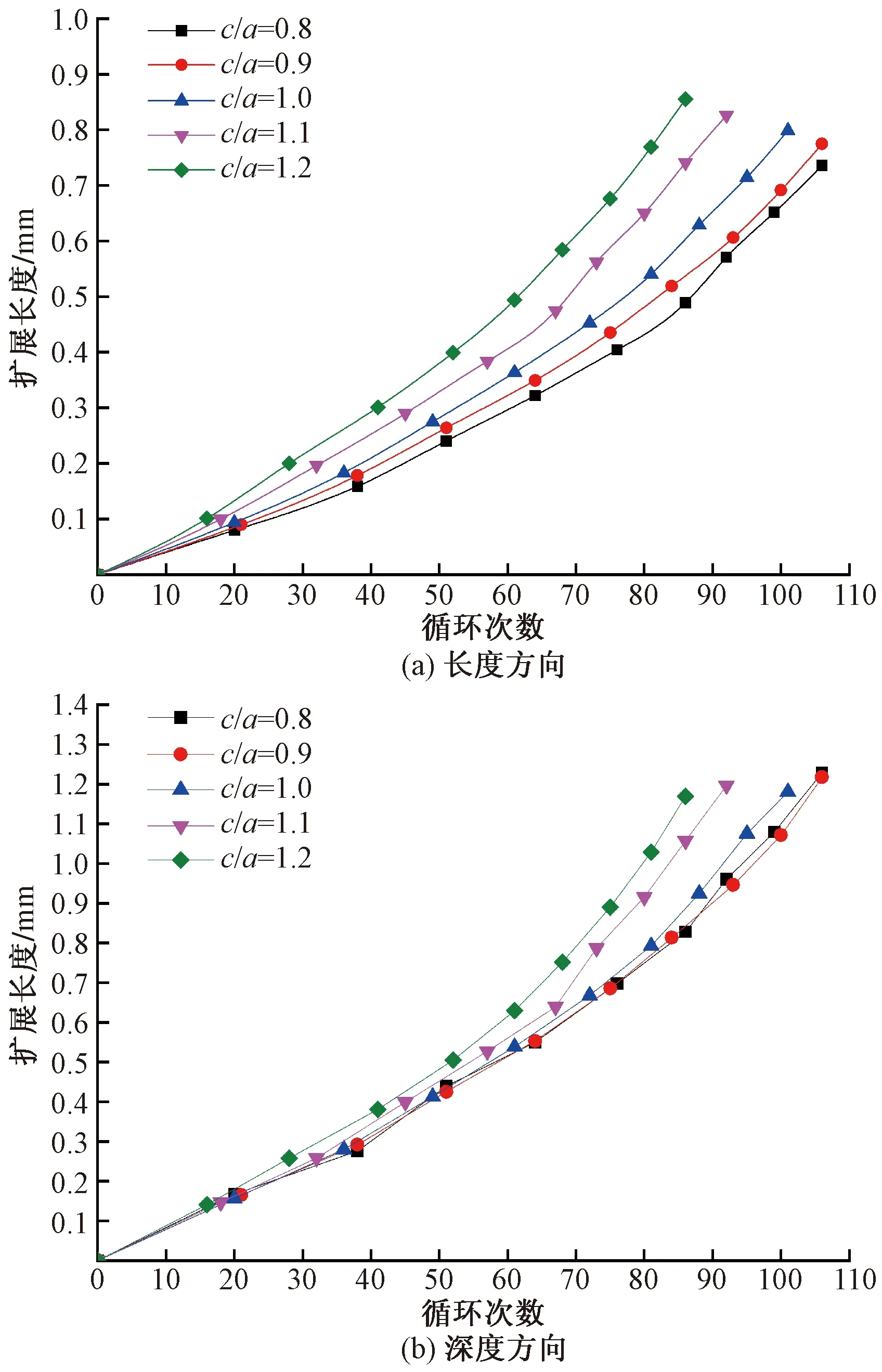
图8 不同长深比的疲劳裂纹长度或深度方向寿命比较
由图8可知,不论沿深度方向或是沿长度方向,其裂纹扩展速率随着裂纹长深比c/a增加而增长,而且扩展距离与循环次数之间呈指数型上升的趋势;但是初始裂纹在疲劳拉伸载荷的作用下刚扩展时,即载荷循环次数在20次以下时,裂纹在深度方向的扩展速率近乎完全相同;而在循环次数10次以下时,沿深度方向的扩展速率亦几乎相同。对于裂纹沿深度方向上的扩展,当长深比c/a≤1时,其扩展速率非常一致,几乎相同;而当c/a大于1时,裂纹的扩展速率则在循环至约70次时明显高于c/a≤1时的情形。而对裂纹沿深度方向上的扩展,其扩展速率则随着裂纹长深比c/a的增加而上升,层次比较分明。总体上看,裂纹沿长度方向上的扩展速率要高于深度方向上的速率。综上,对于主要承受疲劳拉伸载荷的裂纹需要关注裂纹在材料表面处的扩展,同时对裂纹长深比c/a大于1的裂纹扩展要及时采取防止断裂的措施。
4 结论
通过对不同初始长深比c/a的半椭圆裂纹在应力比R=1的疲劳拉伸载荷作用下的扩展规律以及疲劳寿命的研究,得出以下结论。
(1)裂纹长深比c/a仅影响裂纹在初始扩展时的应力强度因子在尖端的分布,即随着c/a由小于1到大于1的过程中,其初始裂纹尖端深度方向上的应力强度因子数值逐渐增长,但总小于裂纹尖端在近表面处强度因子的数值大小。
(2)在裂纹扩展过程中其尖端动态应力强度因子的分布与裂纹初始长深比c/a无关,即裂纹尖端近表面处强度因子数值大小始终高于沿深度方向上的强度因子数值;而且随着裂纹持续扩展,尖端强度因子的极差值越来越大。
(3)裂纹在近表面长度方向上的扩展速率高于沿深度方向上的扩展速率;对于不同长深比c/a的疲劳裂纹,在初始扩展过程中不论其沿深度方向或是长度方向上的扩展速率相同,但随着扩展的进行,裂纹扩展距离呈指数型增长。
(4)当裂纹长深比c/a≤1时,其在表面长度方向上的扩展速率近似相同,但小于c/a>1的情形,而沿深度方向上的扩展速率,则是c/a越高,速率越高。

