加压溶气气浮气含率分布与气泡聚并规律研究

王其玉，雷毛，肖小龙，姚明修，高佳璇，李强*

(1.中石化新疆新春石油开发有限责任公司，东营 257026；2.中国石油大学(华东)新能源学院，青岛 266580；3.山东省油田采出水处理及环境污染治理重点实验室，东营 257026；4.中石化石油工程设计有限公司，东营 257026)

随着工业的发展，油品的消耗日益增长，而在石油开采、炼制及化工生产过程中会产生大量的含油污水，若不能有效对其处理将会对水体和环境造成污染[1]。传统的污水处理方法一般采用重力沉降法[2]，随着工业污水处理技术的发展，高级氧化技术[3]、三维生物膜电极技术[4]等高效水处理技术更受青睐，而气浮法常用于高效处理含溶解性油类或乳化油污水。

气浮法是通过在水中产生微气泡，使油滴粘附在气泡上聚合絮凝并上浮至水面，达到油水分离的目的。气浮法最早用于矿物的浮选，近些年来由于其具有除油率高、处理量大、停留时间短等特点被广泛应用于污水除油等领域[5]。加压溶气法处理污水更节能效果，处理效率可以超过90%，加压过程中，空气溶解量会持续上升，气浮中的气泡量比较多，达到净水的效果[6]。气浮过程中微气泡是影响气浮净化效率的关键，而微气泡与液滴的黏附主要发生在气浮器的接触区，因此接触区的气泡分布和气含率大小对气浮的效果有着重要的影响。

中外学者对溶气气浮的气泡产生分布情况开展了大量研究。郝梦雨等[7]对平流式气浮器进行二维简化，研究了不同进水位置下气相分布，但二维流动与实际差别较大，未分析释放头气液比对气泡的影响。白世兴[8]通过正交试验法优化溶气气浮回流比、溶气量和絮凝剂浓度参数，有效提高溶气气浮的处理效果。时玉龙等[9]研究了微气泡产生过程的机理，在理论上分析了微气泡产生的过程。张义科等[10]通过实验分析各因素对接触区微气泡粒径及气含率分布的影响，研究提高溶气气浮分离效率的最优条件。陈阿强[11]基于实验和数值模拟数据做对比，证明所采用的气泡/油滴黏附动力学模型的合理性，可用于准确预测气浮除油效率及出口含油浓度。Edzwal[12]通过实验研究，提出在气浮过程中气泡的聚并会引起气泡尺寸的变化；Lakghomi等[13]研究了平流式气浮器内气泡聚集，并采用PBM 模型模拟了气浮池中气泡/水两相流动，但并未对气泡聚并情况进行研究分析；Reali等[14]采用microADV技术测量了接触区流动状态，通过与分离效率数据对比，分析了水力负荷、水力停留时间等参数对分离效率的影响。

目前研究主要关注气浮池结构、操作参数及油水种类等因素对浮选除油效果的影响，但对释放头气液比、接触区气泡聚并和气含率分布缺少系统的研究。为此，结合实验研究和数值模拟，分析溶气气浮气泡产生机理、气液比对气含率分布及气泡聚并规律的影响，并从微观角度分析气泡之间的聚并行为规律与宏观气液两相流场之间的关系，以期得到气浮池接触区气含率的分布情况与微气泡聚并之间的内在联系，为设计溶气气浮装置提供参考价值。

1 实验装置及测量方法

1.1 实验装置

实验流程如图1所示，气体通过空压机4进入溶气罐3，与通过进水泵6提升至溶气罐的回流水混合形成溶气水，溶气水通过释放头降压释放产生大量微气泡，在气浮池内进行接触分离，净水回流构成循环。

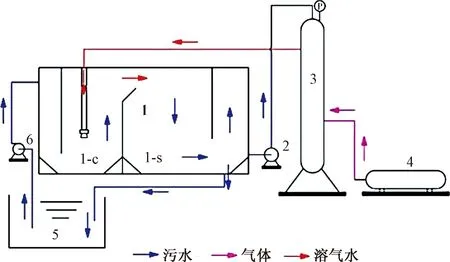
1为气浮池；1-c为接触区；1-s为分离区；2为回流水泵；3为溶气罐；4为空压机；5为水槽；6为进水泵

1.2 气含率测量

如图2所示，采用实验室自制的气含率测量装置，使用前将带刻度的玻璃管C内充满水，将软管A伸入待测区域，管B放入量筒D，在水的重力及虹吸作用下，待测区域含有微气泡的水将通过软管A进入玻璃管C，气体收集在C中，水收集在量筒中，读取玻璃管的前后液位V1、V2及量筒的读数Vw，即可求得气含率为

图2 气含率测量装置

(1)

在溶气压力为0.35 MPa下，多此测量释放头出口气含率，进行重复性验证，测试结果如表1所示。最大相对偏差小于5%，测试误差满足实验要求。

表1 气含率和相对偏差

2 数学模型及数值模拟方法

2.1 控制方程

考虑到加压溶气后装置中的气含率较高，采用了双欧拉模型对接触区内的两相流动进行模拟，并通过相群平衡模型研究气泡的聚并和破碎。

2.1.1 连续性方程和动量方程

相流流动假设在每个网格内各相所占比例之和为1，对于第q项，相输运方程为

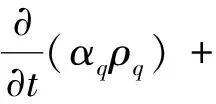
(2)

式(2)中：t为时间，s；q为qth相在计算单元内所占体积分数，其中qth表示第q相；αq为qth的相分数；∇为哈密顿算符；ρq为qth相的密度，kg/m3；vq为qth相的速度，m/s。

动量方程为

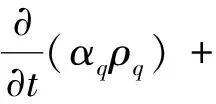
(3)

2.1.2 相群平衡模型

由于气浮器接触区气泡粒径大小不一，并且会随着气泡聚并产生变化，因此加入离散化的相群平衡模型使模拟更加接近实际，该模型的统计方法为

(4)

式(4)中：v为气泡体积，m3；u为速度矢量；n′为数量密度函数；S(v,t)为气泡聚并和破碎得源项。

S(v,t)=Bc(v,t)-Dc(v,t)+Bb(v,t)-Db(v,t)

(5)

v′,t)dv′

(6)

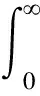
(7)

(8)

Db(v,t)=g(v)n′(v,t)

(9)

式中：Bc与Dc分别为因聚并气泡数目的增长率与消亡率；Bb、Db分别为因破碎气泡数目的增长率与消亡率；v′为不同时刻气泡的体积；a为气泡聚并速度函数；β为气泡体积位于v～v′破碎的概率密度函数；g为气泡破碎速率函数。

2.2 几何模型

数值计算几何模型对应于实验流程图1中的平流式气浮池结构中的接触区，该模型长为400 mm，宽290 mm，高490 mm，其中接触区底部宽为260 mm，具体模型如图3所示。

图3 气浮池接触区模型

2.3 气泡生成及上浮模型

2.3.1 气泡生成模型

在饱和溶气水中，存在着析出的溶解态气体分子聚集形成的气核，压力降低时，溶气水势能降低，气体分子从水分子空隙中逃逸出来形成更多的气核，游离态的气核膨胀形成微气泡[15]。在整个气泡形成过程中，自由能的变化可表示为

(10)

式(10)中：ΔG为气泡自由能；pc为饱和压力，MPa；po为释放处压力，MPa；ngas为形成气核的气体分子个数；ro为初始气泡半径，m；σ为液体的表面张力，N/m；r为生成微气泡的半径，m。

2.3.2 气泡上浮模型

气泡在上浮过程中所受压强的计算公式为

(11)

式(11)中：σwater为液相表面张力，N/m。

由PV=nRT(其中，P为气泡上浮过程中所受压强，Pa；V为气泡体积，L；n为物质的量，mol；R为气体常数；T为绝对温度，K)得

(12)

式中：ρL为水的密度，kg/m3；H为水面高度，m；Z为气泡在静水中所处的位置高度，m。

2.4 求解方法及边界条件

x=190 mm截面处接触区几何模型如图4所示，即释放头中心所在截面，入口释放头直径为20 mm，上表面为水面，底面为z=0截面。在z方向上确定4个接触区不同高度的平面作为实验和数值模拟过程中取样测量的观测平面，每个平面之间间隔为50 mm，测量结果用于分析接触区高度对气浮池内气含率分布的影响。

图4 x=190 mm截面处接触区几何模型

边界条件设置：数值模拟过程中分别设置不同入口气液比的溶气水在一定流速下由释放头流入气浮池，释放头采用速度入口，出口为压力出口，壁面采用无滑移壁面条件，气浮池上表面设置为degassing边界条件，水和气泡分别设置为连续相和分散相，使用瞬态求解器进行求解，收敛的标准是各项参数残差达到10-5，具体设置如表2所示。

表2 具体参数设置

2.5 网格无关性验证

根据实验装置建立模型导入Workbench，以x=190 mm截面为对称面将模型进行切分，并进行网格划分，流体区域采用结构化网格划分。为了在保证计算准确性的前提下选取尽量少的网格数以减少计算量，需进行网格无关性验证。图5为不同网格数量下接触区高度液相速度，可以看出，120 000网格数下液相速度和200 000网格数的相差很小，为了保证网格的质量，同时减少计算资源的浪费，最终选择网格总数为120 648个。网格划分情况如图6所示。

图5 不同网格数量下接触区高度液相速度

图6 网格划分截面图

3 结果及分析

3.1 气液比对不同高度气含率分布的影响

分别在释放头气液比为2%、3%、4%和5%的工况进行实验和数值模拟，得到气液比对气含率影响的关系，比较分析数值模拟和实验结果并进行相关验证。选取x=190 mm接触区截面进行数值模拟分析，如图7所示，并将z方向150～300 mm高度之间设置为气浮池接触区不同高度截面测量位置，每间隔50 mm的高度进行监测，获取不同高度下的实验和数值模拟中气含率分布情况，如图8所示。

图8 气液比对不同高度气含率分布的影响

气浮器实验模型中，释放头的高度为100 mm，由式(10)可推，自由能与气泡半径的关系为

(13)

式(13)中：Vo为气泡体积系数。

由式(13)可知，当自由能较大时产生的气泡粒径较小，因此在气液比较小时，液体流量能够提供较多的初始压力，气体溶解度变大，从而在释放头处产生粒径更小的微气泡。

图7为4种气液比下释放头中心截面处的气液两相流场分布情况。可以看出，当气液比为2%时，气体在水流产生的压力作用下在溶气罐中几乎完全溶解，经释放后在释放头底部形成的高浓度气相域面积最小，当气液比为5%时，形成的高浓度气相域面积最大；相同工况下气液比越低所产生的微气泡粒径越小，2%入口气液比产生的气泡粒径最小，小粒径微气泡上浮速度慢，稳定性好，不易聚并，所以在上浮过程中会发生扩散现象，形成更广泛的气相区域；随着气液比增加，气泡粒径也随之增加，气泡更容易发生聚并，释放头底部会形成更明显的气相域，且在气泡上浮过程中的扩散现象逐渐减弱，但当气液比为5%时，由于气量增加的原因导致气泡上浮到接触区约294 mm高度时会发生明显扩散现象。

图8为不同入口气液比时实验和数值模拟中不同接触区高度下的气相体积分数分布情况。可以看到，在入口气液比相同时，实验和数值模拟中接触区的气相体积分数随接触区高度的变化趋势一致，均随着接触区高度的增加而降低，但实验和数值模拟结果在数值上有一定差距，在实验过程中，溶气罐压力为0.35 MPa，溶气水经释放头流出后还存在部分溶解气未释放，随着接触区高度增加，溶解气含量逐渐减少，将气浮池内流体引入到气含率测量装置时，溶解气则会进一步释放，导致实验测量的气含率偏高，随着接触区高度增加，这种差距会逐渐减小。150 mm高度处对应不同入口气液比条件下气相体积分数均是最大，这是由于气泡在上升过程中，受到湍流扰动的影响，尤其是在气液比为4%和5%时气泡更容易发生聚并的现象，形成大粒径微气泡，使得气泡在水中上浮速度快、稳定性差，当气量大时气相容易发生扩散和逸出界面，导致局部气相体积分数降低；当接触区高度相同时，随着入口气液比增加，实验和模拟结果中接触区的气相体积分数均随气液比增加而相应升高，特别是在入口气液比为2%和3%时接触区气相体积分数上升幅度更为明显，这是由于气液比增加，气泡粒径变大，气泡发生聚并而不易发生扩散，同一高度截面上气量也随之增加，截面气泡体积占比更多，气泡密度更大，因此气含率也随之变大。

3.2 微气泡聚并现象研究

为了更详细的了解气泡的聚并现象，在相同区域分别以大间距和小间距并行排列两个相同直径的微气泡，模拟其上浮过程中的聚并情况，如图9、图10所示。另外，为了对比气泡大小对聚并的影响，分别模拟了不同粒径的气泡的上升过程，其中大粒径气泡直径D=500 μm，小粒径微气泡直径d=60 μm。

t0为初始时刻，单位：ms；Δt为气泡上浮的时间，单位：ms

图10 并行排列的小间距微气泡上浮过程

可以看出，当500 μm气泡间距为3D时，两个气泡会规律的靠近与远离，不会发生聚并，相比于60 μm的气泡，大直径气泡的浮力较大，上升较快。当大直径气泡间距为2D时，两个气泡会发生聚并，但60 μm气泡在间距为2d时未发生聚并，气泡直径越小，发生聚并时的气泡间距更小，因为当气泡的物理尺度很小且上升速度很慢时，局部雷诺数和韦伯数都很小，使得上升过程中的惯性力几乎可以忽略不计，流场中的扰动很小，表面张力的作用显著。因此，由于表面张力很大，而流场扰动又很小，气泡的形状很难发生变形，而随着气泡直径变小，表面张力更大，流场扰动更小，气泡更难发生聚并。

图11给出了不同间距上下排列的微气泡的上浮运动过程。可以看出，气泡在间距为1.5D时发生聚并，但间距为2D时上面气泡优先逸出界面，可知，上下排列气泡仍然只在较小的间距内发生聚并。

图11 不同间距的上下排列的微气泡的上浮过程

4 结论

模拟计算了溶气气浮器内气液两相流动及气泡聚并现象，从宏观和微观角度研究了气泡聚并及气含率分布规律，分析了释放头气液比和接触区高度对气含率的影响，且实验结果验证了数值计算的正确性。得出如下结论。

(1)气液比为2%时，空气几乎完全溶解，经释放头能产生小粒径微气泡，不易聚并且会发生扩散现象；气液比为5%时，气泡粒径也随之变大，气泡发生明显聚并现象，并伴随气相扩散现象。

(2)当气液比不变时，实验和数值模拟中接触区的气相体积分数均随着接触区高度的增加而降低。从微观角度分析气泡在上浮过程中，由于大量小间距微气泡的存在，使气泡之间发生剧烈聚并，气泡粒径逐渐增大，提高局部气相体积分数。

(3)当高度不变时，实验和模拟结果中接触区的气相体积分数均随气液比增加而升高，气液比为2%和3%时气相体积分数上升幅度更为明显，由于气液比增加，气泡粒径变大，气泡更容易发生聚并而不易发生扩散。

(4)当气液比或接触区高度增加时，气泡粒径由于聚并和体积膨胀不断增大。而60 μm微气泡的局部雷诺数和韦伯数都较小，相比于500 μm气泡较难发生聚并，气泡粒径越小，聚并所需距离更小。