台阶式消能设计中相关参数的敏感性分析
姜 啸
(秀山县水利电力勘测设计院,重庆 409900)
1 引 言
台阶式消能工在水库、电站、拦河闸坝甚至灌溉渠道工程的泄水建筑物中都有应用,尤其是在数目众多的小型工程中更为常见。台阶式溢流坝模型试验结果表明:其消能率超过光滑坝面[1]。如果充分利用溢流面消能,则溢流面出口流速降低,下游消力池长度缩短,这样不仅节约工程布置空间,并且结构简单、施工难度小。台阶式消能工理论研究较多[2],《混凝土重力坝设计规范》(SL 319—2018)的条文说明指出可参考《水工设计手册》(第2版)第7卷中的相关公式进行初步设计时的水力计算[3]。至此,台阶式消能在设计过程中具有了规范性质的理论支撑依据。
通过引入不确定性分析方法,以台阶式消能的效率为分析指标,对溢流面坡度、单宽流量和溢流面净高等不确定性因素采用昌桑(H.Chanson)计算法(以下简称昌桑算法)进行测算,并分析不确定性因素对消能效果的敏感程度,推断其中相对主要的敏感因素。为溢流面消能方式的比选和水工结构体型的优化提供一定参考。
2 昌桑算法简介
根据《水工设计手册》(第2版)第7卷:当通过台阶下泄水流形成滑移流流态时,可按昌桑算法进行台阶消能水力学计算。
均匀流水深为
(1)
式中:f为摩擦系数;q为单宽流量,m3/(s·m);α为泄槽的坡角,(°)。
摩擦系数为
(2)
式中:k*为糙度,k*=hcscα;q为单宽流量,m3/(s·m);其他参数含义同上。
堰顶至表面掺气起始断面的长度L1、断面水深d1和平均流速v分别为
(3)
(4)
形成全断面均匀掺气水流的距离为
(5)
均匀掺气水流系数分别为
ce=0.9sinα
(6)
(7)
fe=0.5(1+tanhx)
(8)
式中:tanhx为双曲正切函数。
稳定掺气区的均匀流掺气水流的水深d0、相应断面的平均流速v0分别为
(9)
(10)[4]
3 消能率计算公式简介
溢流面出口断面的消能率为
(11)
E=H堰+H
(12)
式中:H堰为溢流面净高,m;H为堰上水头,m;其余符号意义同前[4]。
4 敏感性分析法简介
敏感性分析是一种定量风险分析,将项目结果的变化与定量风险分析模型中输入的变化建立关联,从而确定产生最大潜在影响的项目风险或不确定性来源。敏感性分析可从若干不确定性因素中逐一找出对分析指标有重要影响的敏感性因素,并通过计算分析重要因素对效益指标的影响程度和敏感性程度[5]。主要分析步骤如下:
a.初选台阶式消能率的不确定因素。
b.确定台阶式消能率的不确定因素变化程度并计算相应的敏感性系数。
c.计算变化后的不确定因素,并将所得评价指标与基本方案评价指标进行对比分析。
d.归纳敏感性分析的结论,推断相对主要的台阶式消能工敏感因素之间可能存在的关联,指出最为关键的几个敏感因素,针对敏感性分析结果中不确定因素的影响,提出相应的减轻措施。
对台阶式消能工的消能效果进行量化分析,可避免只能按经验进行定性分析,或仅仅将台阶式消能工的消能率当作联合消能中的安全储备,有助于在消能效果变化与分析模型中的要素变化之间建立联系,并确定对其消能效果具有相对较大的潜在影响的不确定性来源。
5 台阶消能工基本模型及不确定性因素选取
以小(2)型工程观音阁水库初步设计推荐方案为例,其永久挡水建筑物推荐坝型为重力坝,属于4级水工建筑物。其溢流坝段在设计洪水位工况下,堰上水头Hw=1.66m,下泄流量Q=60.6m3/s。溢流坝段的溢流面净高H堰=21.5m、净宽B堰=16m。为了减小大坝溢流面出口的流速,防止泄洪时坝趾被冲刷,同时缩短溢流面出口设置的消力池长度,考虑在大坝溢流面内设置消能台阶。初步拟定溢流面坡度为1 ∶0.9,设计溢流面坡长L=26.9m,台阶的步高h=0.6m、步长l=0.54m。按照前述公式计算得到消能后出口断面的水深d2、该断面平均流速v2及其消能率η,见表1。
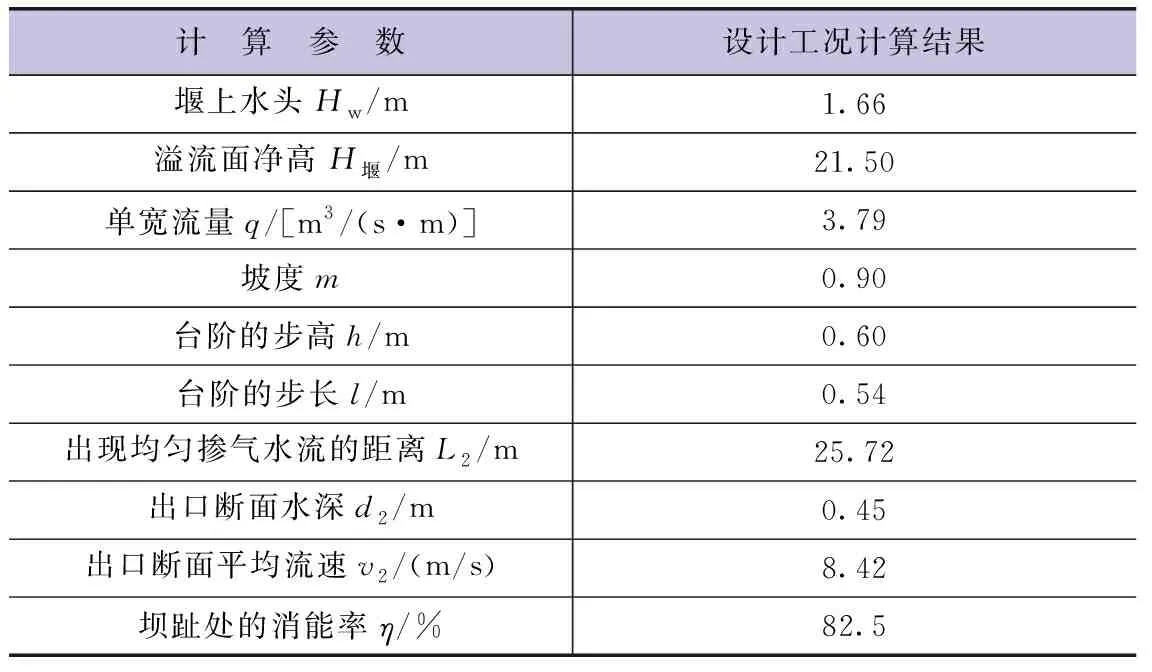
表1 台阶消能工基本模型计算结果
根据昌桑算法公式组成,同时结合台阶式消能工结构特点,影响台阶式溢流面的水力学参数包括单宽流量、溢流面净高,溢流面的坡比(或坡角)、台阶断面几何尺寸等[6]。
因此,分别选定台阶步高h、溢流面的底坡m、设计洪水位工况下的单宽流量q和溢流面净高H堰等4项作为不确定因素[7],并采用昌桑算法对同一工程算例进行计算,比较在以上影响因素相同的设计条件下,当溢流面形成滑移流流态时,消能率的不同,并确定其偏离基本情况的程度。
6 不确定因素变化程度的确定及对应消能率的计算
为观察各种变化对分析指标的影响,将台阶式消能工消能率的变化与分析模型中输入的不确定因素变化建立关联,分别选择不确定因素变化的±10%、±20%、±30%、±40%和±50%作为不利和有利的变化程度,以便计算敏感性分析指标,并编制敏感性分析表或绘制敏感性分析图。从而确定对台阶式消能工消能效果产生最大潜在影响的不确定性来源[8]。
溢流面台阶步高尺寸从增加50%到减少50%时,消能率计算结果见表2。
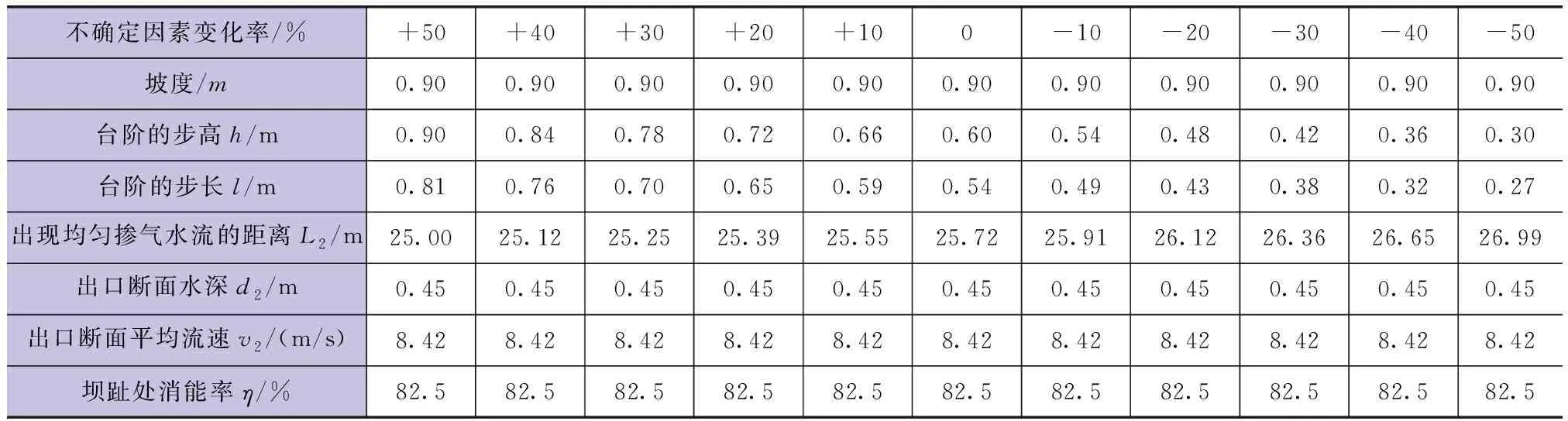
表2 基本模型台阶尺寸变化的计算结果
溢流面坡度从增加50%到减少50%时,消能率计算结果见表3。
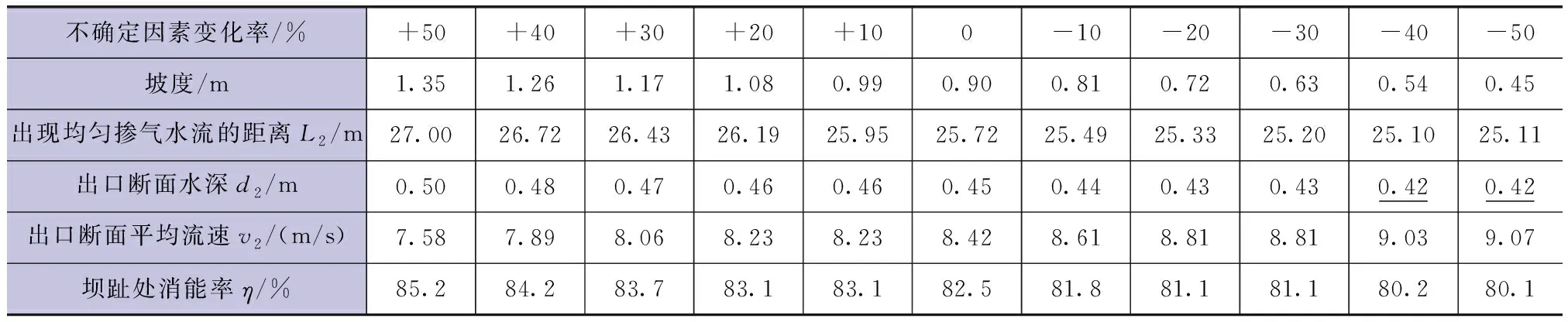
表3 基本模型溢流面坡度变化的计算结果
单宽下泄流量从增加50%到减少50%时,消能率计算结果见表4。
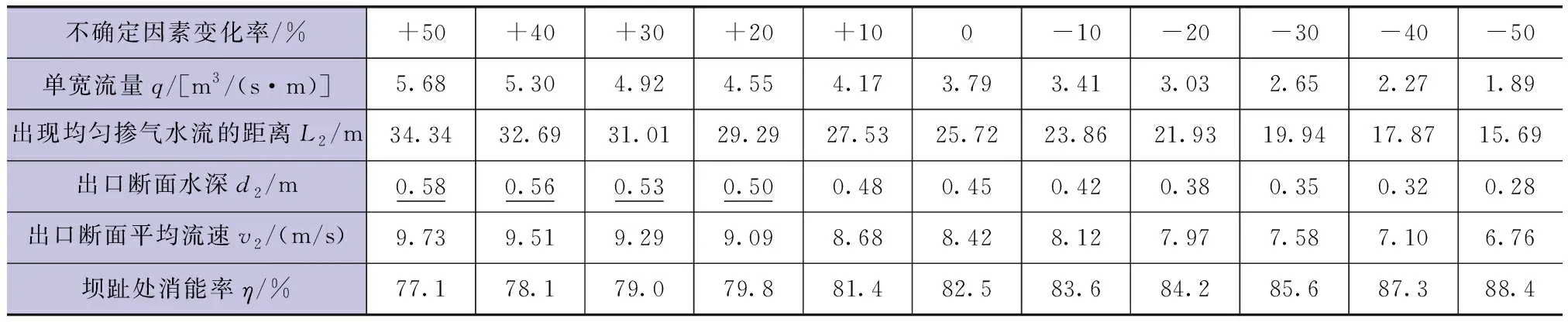
表4 基本模型单宽下泄流量变化的计算结果
溢流面净高从增加50%到减少50%时,消能率计算结果见表5。
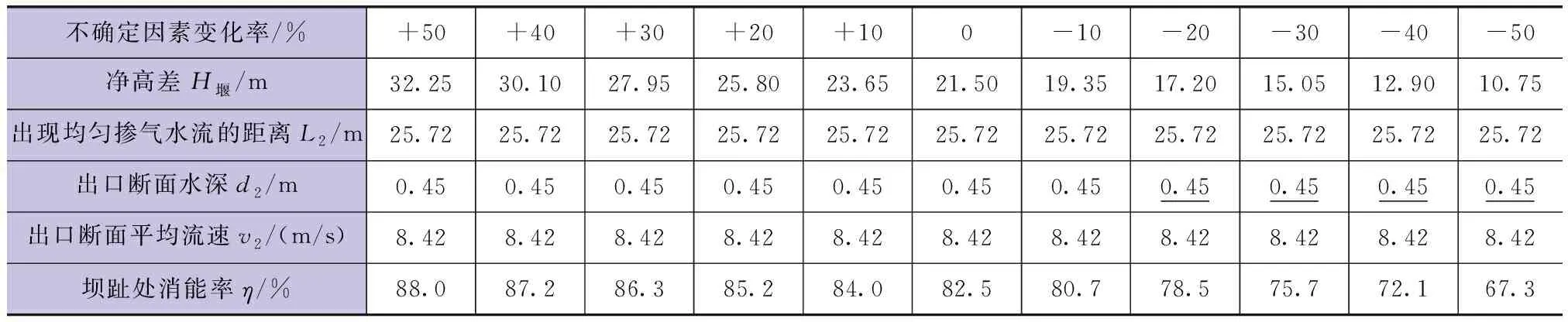
表5 台阶消能工模型溢流面净高变化的计算结果
7 敏感性分析指标计算结果表述和分析
敏感度系数是项目分析指标变化的百分率与不确定因素变化的百分率之比。敏感度系数计算公式如下:
(13)
式中:E为分析指标A对于不确定因素F的敏感度系数;ΔA/A为不确定因素F发生ΔF/F变化时,分析指标A的相应变化率,%;ΔF/F为不确定因素F的变化率,%[9]。
本例以消能率η作为分析指标,分别计算台阶尺寸、溢流面坡度、单宽下泄流量和溢流面净高等不确定因素的敏感度系数,结果见表6。
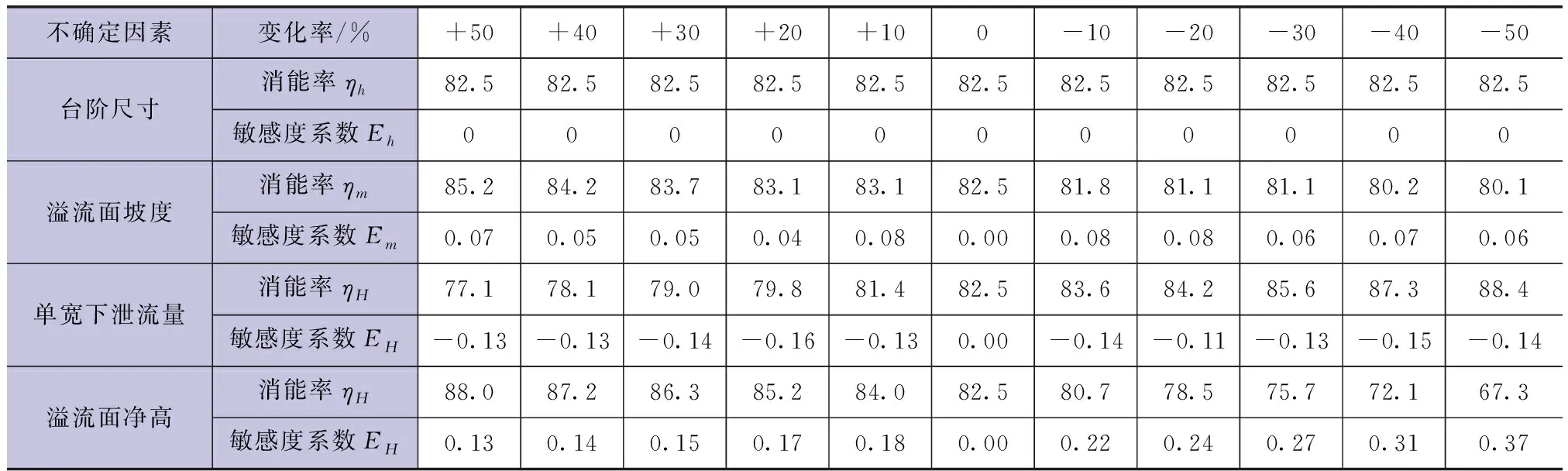
表6 敏感性分析指标计算成果
本例采用昌桑算法计算台阶式消能工消能效率时,由本算例计算成果表和图1可知:ⓐ台阶步高从增加50%到减少50%时,其敏感度系数Eh均为零,台阶尺寸变化未导致消能率发生改变,故台阶尺寸为非敏感性因素;ⓑ溢流面坡度从增加50%到减少50%时,其敏感度系数Em为0.06~0.08,均大于零;溢流面坡度系数递减,溢流面坡度变陡,消能率降低,该不确定因素与分析指标同方向变化;ⓒ单宽下泄流量从增加50%到减少50%时,其敏感度系数Eq为-0.11~-0.16,均小于零;单宽下泄流量递减,消能率提高,该不确定因素与分析指标反方向变化;ⓓ溢流面净高从增加50%到减少50%时,其敏感度系数EH为0.13~0.37,均大于零;溢流面净高递减,消能率降低,该不确定因素与分析指标同方向变化;ⓔ比较溢流面坡度、单宽下泄流量和溢流面净高的敏感度系数的绝对值,可以看出Eq略低于EH,Em则明显小于Eq和EH,说明溢流面坡度比单宽下泄流量和溢流面净高对消能率指标的影响程度相对较小。即以消能率为考察指标,其对单宽下泄流量和溢流面净高的敏感程度大于对溢流面坡度的敏感程度,单宽下泄流量和溢流面净高是较为敏感的不确定因素。因此,在设计方案中,应更加重视单宽下泄流量和溢流面净高对溢流面消能方式的布置比选和水工结构体型优化的影响。
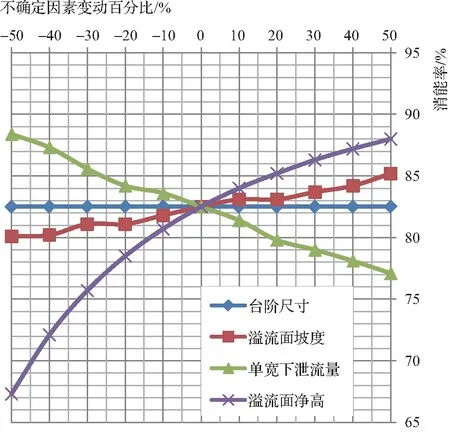
图1 台阶消能工敏感性分析
8 对比分析单宽下泄流量q、溢流面净高H堰变化对消能率的影响
由前述可知,单宽下泄流量q和溢流面净高H堰是台阶式消能工设计的关键参数,对消能率影响较大。推断这主要是由于采用昌桑算法时,出口断面水深d与临界水深dc有关,而临界水深dc可由单宽下泄流量q求得;同时,从堰顶算起至开始出现表面掺气处的长度L1和出现均匀掺气水流的距离L2受溢流面净高H堰影响。
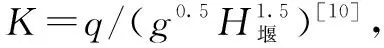

表7 流能比计算成果
9 结 语
综上所述,通过具体的算例结果进行推断,台阶尺寸为非敏感性因素。溢流面坡度系数与消能率同方向变化;单宽下泄流量与消能率反方向变化;溢流面净高与消能率同方向变化。消能率指标对单宽下泄流量和溢流面净高的敏感程度大于对溢流面坡度的敏感程度,是较为敏感的不确定因素。
由此可见,在初步设计中,调整泄水建筑物体型或提高工程规模有利于发挥台阶式溢流面的消能效果,比如通过适当增加溢流面宽度以降低单宽下泄流量,或者适当增加防洪库容、提高调蓄能力,减小下泄流量等手段,能使水工建筑物消能工结构的设计得以优化和完善。

