稀疏多径下基于PASR的涡旋电磁波传输特性

李嘉欣，赵恒凯

（上海大学通信与信息工程学院，上海 200444）

0 引言

携带轨道角动量（Orbital Angular Momentum，OAM）的涡旋电磁波因其模态间相互正交的物理特性，具有提高未来无线通信系统传输容量和频谱效率的潜力，引起了研究者们的广泛关注。1992年，Allen等人[1]在研究拉盖尔—高斯（Laguerre-Gaussian，LG）波束时发现了其携带轨道角动量。从数学表达式上看，是在传统平面电磁波表达式的基础上乘以了一个旋转相位因子exp(ilφ)（其中，l表示OAM模态，φ表示方位角），在结构上表现为其相位波前具有围绕波束轴的空间螺旋结构，故被称作涡旋电磁波[2]。

涡旋电磁波是中空波束，其波束中心的场强为零。随着OAM的模态及传输距离的增大，涡旋电磁波会逐渐向外扩散，波束中心的中空区域也变得更大。如果在接收端采用完整的圆形阵列天线进行接收，那么天线的尺寸将非常大，在实际应用中较难实现。为解决这一问题，Hu等人[3]提出了部分孔径取样接收（Partial Angular Sampling Receiving，PASR），该方案结合了光学领域的部分孔径接收与采样接收理论，将接收天线阵元均匀地分布在OAM波束强度最大的一段圆弧上，并将每个天线看作采样点。Hu等人通过仿真实验证明了该PASR方案能够实现不同模态OAM波束的接收和解复用，验证了其在长距离传输情况下的可行性。

OAM技术提供了新的空间复用方法，为缓解无线频谱资源紧缺的问题提供了新的解决方案，在第六代移动通信（6th-Generation，6G）系统中显示出了巨大的发展潜力[4-5]。为进一步推动OAM复用技术的实际应用，研究并分析其信道传输特性十分必要。而实际的无线信道环境较为复杂，多径反射、散射和绕射等现象不可避免，已有相关研究[6-7]证明了反射等引起的多径效应会造成OAM波束的相位畸变，从而破坏空间中各模态OAM波束间的正交性，引起OAM模态的扩散，造成模态间干扰问题。2020年，L.Liang等人[8]在仅考虑小于等于三次的反射路径的稀疏多径环境下，提出了将OAM多路复用与正交频分复用技术（Orthogonal Frequency Division Multiplexing，OFDM）相结合，称为混合正交分割复用（Hybrid Orthogonal Division Multiplexing，HODM）。其研究结果表明，HODM方案不仅能减弱多径效应对涡旋系统性能的影响，还大大提升了传输容量。在文献[9]中，作者建立了基于非视距场景下OAM-MIMO系统模型，为减轻多径造成的不同OAM模态间的干扰问题，提出了一种低复杂度的预发射和预接收传输方案，仿真结果说明了当信噪比大于7dB，采用该预处理方案的OAM-MIMO系统比未采用该方案的系统的信道容量更高，证明了该方案的可行性。2020年，Su等人[10]基于太赫兹无线通信链路，分析了多径效应及接收机孔径大小对多路复用OAM系统传输性能的影响，证明了多径效应以及有限的接收孔径会导致OAM相邻模态间的功率耦合，从而造成信道内及信道间串扰问题。

可以发现目前基于多径信道的研究，大多集中在如何抵抗多径效应对OAM传输性能影响等方面，针对OAM波束发散特性导致的长距离接收困难问题并未给出解决方案和分析。因此，本文对采用PASR方案的涡旋波束在稀疏多径高斯信道中的传输特性展开了研究，重点分析了多径数目、天线阵列数目、传输距离等参数对基于PASR方案的涡旋系统传输性能的影响，证明了PASR涡旋通信系统在长距离稀疏多径环境中的可行性。

1 完整孔径取样接收及部分孔径取样接收简介

1.1 WASR方案

采用均匀圆阵列的来接收涡旋波束，即完整孔径取样接收（Whole Angular Sampling Receiving,WASR）方案是对整个圆形接收区域内的信号进行采样，其模型如图1所示[11]。在接收端，M个天线阵元均匀地分布在接收天线的整个圆孔径上，则第m个接收天线的方位角可以表示为φm=2πm/M,m={0,1,…,M-1}。在本文的推导中，假设接收和发射天线的初始相位角均为0。

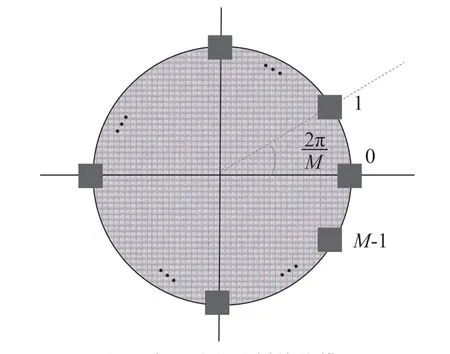
图1 完整孔径取样接收模型

若发射端有N个天线阵元，令ln表示发射的第n个OAM模态，则采用WASR方案接收的信道的归一化矩阵可以表示为：

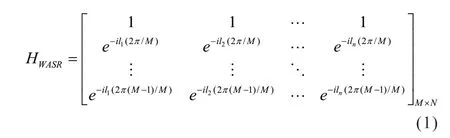
通过计算各个子信道之间的关系，可以得到WASR方案的正交OAM模态集合。第n1和第n2(n1,n2∈{0,1,2,…,N-1}且n1≠n2)个传输子信道的相关关系可以通过式（1）归一化矩阵对应列的内积得到，即：

根据式（2）可知，为使所有传输OAM模态之间相互正交，对于WASR方案中的任意一对n1和n2，内积应等于0，则它们的模态间差值ln1-ln2应满足：

即对于WASR方案，任意两个OAM模态差值应满足：不是接收天线数M的整数倍，就可以保证各模态OAM波束之间的正交性，从而使接收到的OAM波束被正确地解复用，这也表明了分布着M个阵元的接收阵列天线最多能接收解复用M路OAM信号。

1.2 PASR方案

部分孔径取样即PASR方案，是将天线阵元仅集中在接收端的一段弧上，接收端仅需要接收一部分涡旋波，就可以实现对OAM的解复用[12]。PASR模型如图2所示，M个天线阵元均匀地分布在接收天线的的1/K圆弧上，则第m个接收天线阵元的方位角表示为φ'm=2πm/MK,m={0,1,…,M-1}。

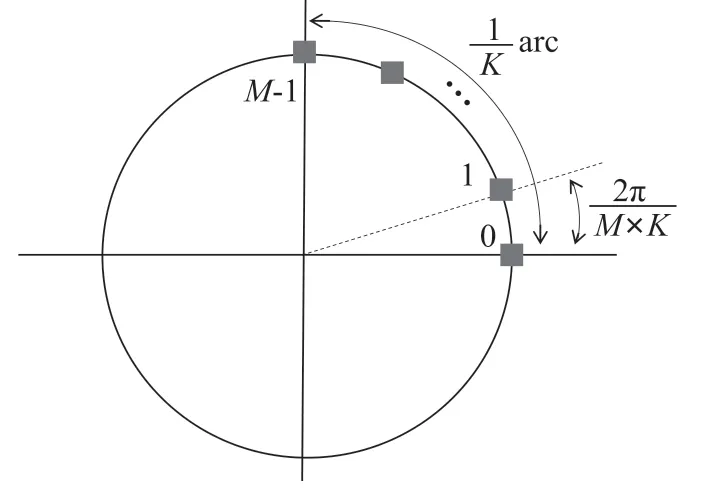
图2 部分孔径取样接收模型

PASR方案的第n1和第n2(n1,n2∈{0,1,2,…,N-1}且n1≠n2)子信道的相关关系为[11]：

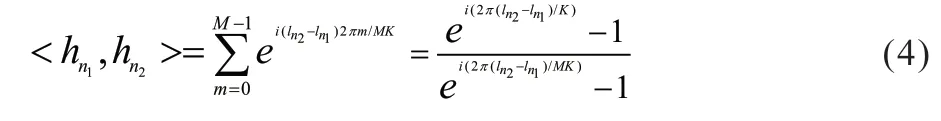
根据式（4），为保证所有传输OAM模态间的正交性，对于PASR方案中的任意一对n1和n2，它们的模态间差值ln1-ln2应满足：

即对于PASR方案，任意两个OAM模态差值应满足：所复用的多路OAM信号的模态间差值满足是K的整数倍但不是M×K的整数倍。

2 基于稀疏多径的OAM部分取样接收系统模型

本节建立了基于PASR方案的OAM无线通信系统模型，涡旋波束在如图3所示的稀疏多径场景中传输，包括直射径和由镜面反射造成的反射路径。

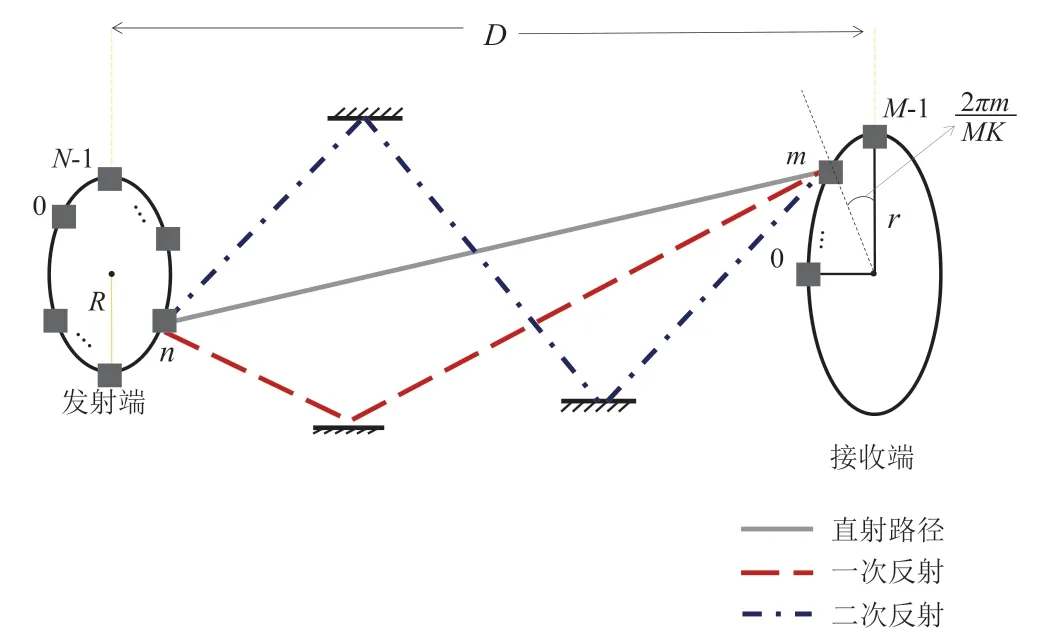
图3 稀疏多径场景下PASR涡旋通信系统模型

本文的稀疏多径场景包含一条直射径、P条一次反射径和S条二次反射径。故总路径数目可以表示为：

在自由空间中，发射端第n个阵元到接收端第m个阵元的信道幅度增益[13]可以表示为：

其中，λ为波长，β表示所有相关常数，dmn为第n个发射阵元与第m个接收阵元间的距离。

对于直射径，第n个发射阵元与第m个接收阵元间的距离表示为[14]：

同理，对于一次反射径和二次反射径，第n个发射阵元与第m个接收阵元间的距离d1和d2分别表示为：

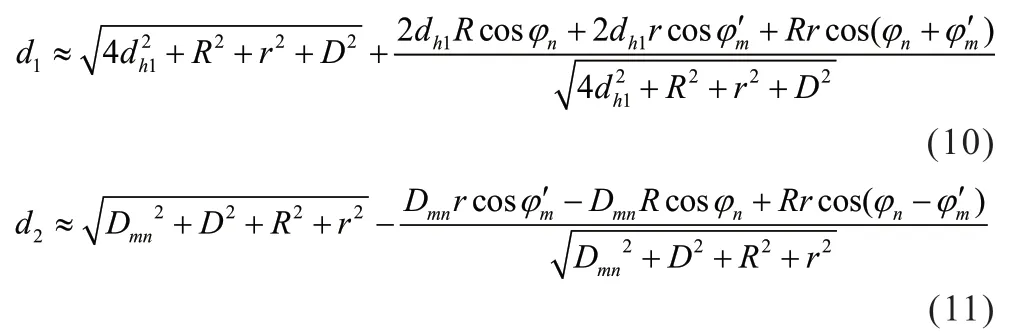
其中，dh1为发射端UCA中心到一次反射面的距离，Dmn的表达式为：

其中，接收端U C A 中心到二次反射面的距离为dh2，dr1r2表示两个反射面间的距离。将式（9）、（10）和（11）代入式（7），可以得到各路径的信道幅度增益h0、h1及h2。

为便于分析，引入贝塞尔函数对接收端的涡旋波束信号作进一步近似处理，l阶第一类贝塞尔函数的表达式为：

涡旋波束具有经奇数次反射后模态值符号会发生反转的性质。因此，当发射端发射模态为l0的OAM波时，接收到的波束可以看作由来自于直射径的模态为l0的OAM波、来自于一次反射径的模态为-l0的OAM波以及来自于二次反射径的模态为l0的OAM波组成[15]。故稀疏多径环境下，第m个接收天线阵元上接收到的OAM信号可以表示为：

其中，sl0表示第l0个模态上的传输信号，wm表示接收UCA第m个阵元上服从均值为0、方差为σm2的高斯白噪声，LPASR表示满足PASR方案的传输OAM模态集合，即传输的各模态间差值满足：是弧段数K的整数倍但不是M×K的整数倍。基于上述推导，可以得到OAM模态为l0的信道容量为：

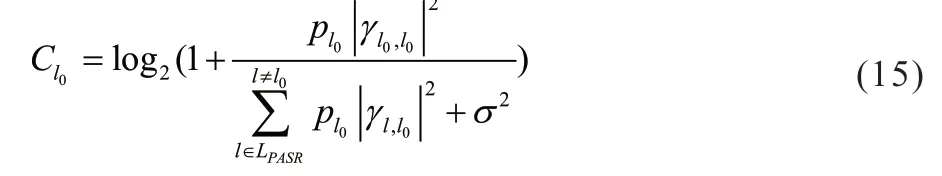
其中，pl0是携带l0模态的涡旋波的发射功率，σ2为噪声信号的方差，表示l0模态的传输增益，表示其他模态对l0模态所产生的信道干扰。

故稀疏多径场景下的PASR涡旋系统的传输容量为：

3 仿真结果与分析

本文的研究对象选取典型且易于实现的LG波束，其数学表达式为：

本文利用MATLAB仿真分析了多径数目、天线阵列数目、传输距离等参数对基于PASR方案的涡旋系统传输性能的影响。仿真参数设置如下：LG波束束腰半径ω0=0.01，工作频率f=30 GHz，相关常数β=π，PASR采用1/4圆弧，发射及接收UCA半径分别为R=10 m、r=20 m。

3.1 多径数目对OAM模态功率谱的影响

首先分析了多径数目对OAM模态功率谱的影响。图4是不同多径数目下，OAM模态分别为l=1、l=3的OAM模态功率权重。相关仿真参数设置为：传输距离D=100 m。首先，当OAM模态值相同时，OAM模态权重随着反射路径数的增加而减小，这是由于多径效应会造成OAM波束的相位畸变，信道内的串扰问题变得更为严重。其次，当多径数目相同时，OAM模态值越大，本身模态的功率权重越小，其他模态的权重变大。这与涡旋波模态阶数越高、波束发散越严重的特性相关，发散性增强导致反射路径的OAM波束功率增大，从而增大了模态间的干扰。因此对于模态值较高的OAM波束而言，在多径信道中传输时，接收端解调的难度也会大大增加。

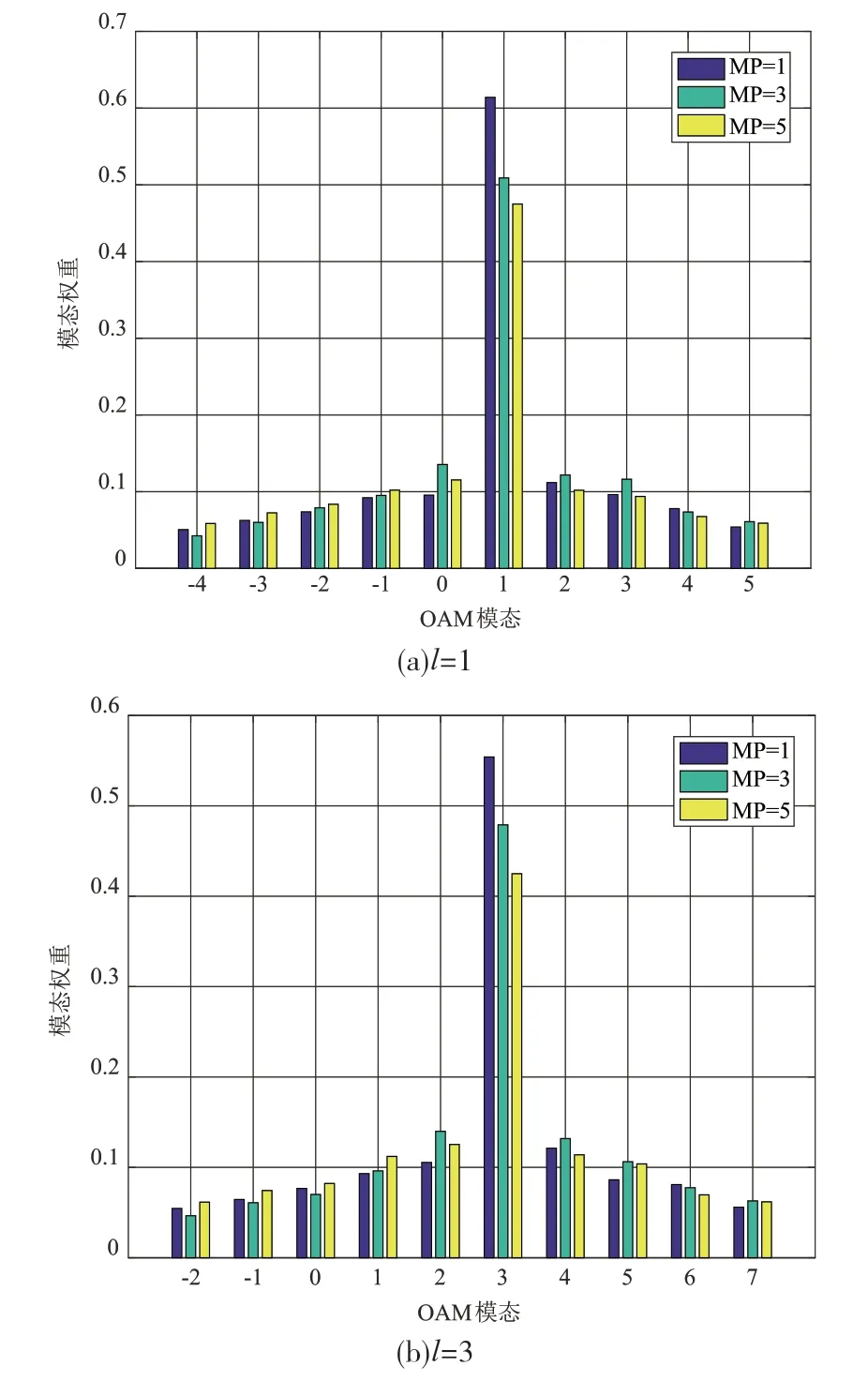
图4 多径数目对不同OAM模态功率谱的影响

3.2 多径数目对信道容量的影响

接下来分析了多径数目对基于PASR方案的OAM涡旋系统传输容量的影响。图5给出了在不同多径数目下，OAM模态分别为l=1、l=3的涡旋系统信道容量随信噪比变化的曲线图。相关仿真参数设置为：传输距离D=100 m，收发端阵元数为4×4，一次反射径的数目P及二次反射径的数目S的具体设置如图所示。从仿真结果可以看出，在一定程度上，OAM系统的信道容量随着反射路径数目的增加而增大，这是因为信道幅度增益与多径数目相关，传输路径越多，信道幅度增益越大。同时，对比图5(a)和图5(b)还可以发现，传输的OAM模态越大，信道容量越小。对于携带较低模态的OAM波束而言，在稀疏多径场景下传输更具有优势，这也验证了图4得到的结论。

图5 不同多径数目下不同模态的涡旋系统信道容量

3.3 天线数量对信道容量的影响

接下来对比了采用不同接收方案的OAM涡旋系统的传输性能。图6是在不同天线阵列数目下，PASR和WASR的信道容量随信噪比变化的曲线图。相关仿真参数设置为：传输距离D=100 m，OAM模态值l=1，多径数MP=3，其中P=S=1。从仿真结果可以看出，无论接收端采用PASR方案还是WASR方案，涡旋电磁波系统的信道容量均随着阵列天线数量的增多而变大，原因考虑以下三个方面：首先，阵列天线数量越多，其带来的阵列天线增益就越大；其次，发射天线数量越多，产生的涡旋电磁波越连续；此外，接收端天线数量越多，接收到的能量也更多。因此，适当地增加收发端阵列天线数量可以有效地提升OAM系统的信道容量。

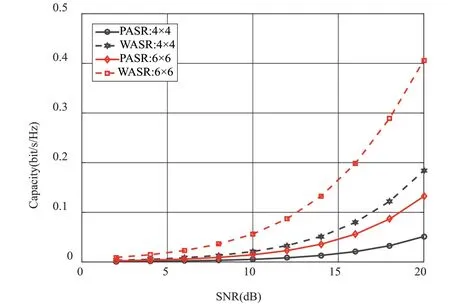
图6 不同天线数目下PASR和WASR信道容量对比图

3.4 传输距离对信道容量的影响

图7给出了在不同传输距离下，PASR和WASR的信道容量随信噪比变化的曲线图。相关仿真参数设置为：OAM模态值l=1，收发端阵元数为4×4。可以看出，当信噪比相同时，传输距离越大，PASR和WASR的信道容量越小，这是OAM波束的远距离传输下的发散特性造成的。

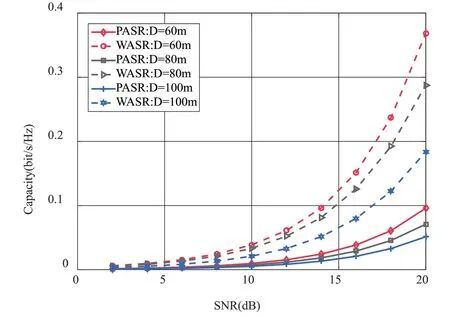
图7 不同传输距离下PASR和WASR信道容量对比图

为进一步对比PASR方案和WASR方案在长距离传输下的容量的变化趋势，提出了利用相对系数η来表征PASR方案和WASR方案信道容量的相对差异，η的表达式为：

相对系数η越小，表示PASR方案和WASR方案的信道容量间的相对差值越小。从仿真结果可以得到，在信噪比为20dB情况下，D=60 m时，η=0.597；D=80 m时，η=0.573；D=100 m时，η=0.554。即随着传输距离不断增大，η的值越来越小，说明了PASR方案相较于WASR方案而言，在远距离传输情况下的容量衰减程度更小。

因此，在OAM波束远距离传输时，采用PASR方案的接收天线尺寸仅为采用WASR方案的1/4，大大提升了资源利用率，同时传输容量与采用WASR方案相比，在远距离传输情况下衰减程度更小，从而说明了在稀疏多径环境中PASR涡旋通信系统的可行性。

4 结束语

本文基于涡旋电磁波的基础理论，建立了采用部分孔径取样接收方案的稀疏多径涡旋电磁波传输模型，并利用MATLAB仿真分析了LG波束在稀疏多径环境中传输时，多径数目、天线阵列数目、传输距离等参数对模态权重、信道容量的影响。仿真结果证明了PASR涡旋通信系统的信道容量随传输距离的变大，衰减程度更小，由此说明了在长距离稀疏多径环境中传输时，PASR涡旋通信系统具有更好的稳定性。同时，考虑将OFDM技术与OAM多路复用相结合，以抵抗多径效应对PASR涡旋通信系统的影响，进一步提高传输容量将是未来的研究重点。