基于二次分解重构策略的航空客流需求预测

栗慧琳，李洪涛，李 智

（兰州交通大学 交通运输学院，兰州 730070）

0 引言

随着中国经济的快速发展和人民生活水平的逐步提升，大众出行方式的选择发生了重要变化，航空运输业以其快速、舒适、便捷等特点日益受到人们的青睐。近年来，我国的航空客运需求不断增长，给航空运输保障工作、机场建设规划管理以及航空公司市场发展带来了一系列的机遇和挑战。各国政府和市场参与者必须准确预判航空客流需求的变化情况，对未来发展做出战略性规划，在合理利用资源、满足运输需求的同时，为航空所在地区创造更大的经济和社会价值［1］；而航空客流需求受诸多复合因素共同影响，在数据上呈现一定的波动性、不规则性和不稳定性，这使得准确预测航空客流需求成为一项艰巨的任务。

在此背景下，国内外众多学者对航空客运需求预测进行了研究，取得了若干成果。当前对航空客运需求的研究主要集中在定量预测方面，常用的方法有计量经济模型（如Holt-Winters［2］、自回归单整移动平均（AutoRegressive Integrated Moving Average，ARIMA）模型［3］、自回归单整移动平均季节（Seasonal ARIMA，SARIMA）模型［4］、广义自回归条件异方差（Generalized AutoRegressive Conditional Heteroscedasticity，GARCH）模 型［5］和全局 向量自回归（Global Vector AutoRegression，GVAR）模型［6］等）和人工智能模型（如反向传播神经网络（Back Propagation Neural Network，BPNN）［7］、支持向量机（Support Vector Machine，SVM）［8］、回声状态网络（Echo State Network，ESN）［9］、长短期记忆（Long Short-Term Memory，LSTM）网络［10］等）。上述研究成果都为航空运输业的发展提供了一定参考价值，然而经济发展、地理人口、市场结构以及政策调整等诸多因素都会影响航空客流需求数据。为了提高预测方法的准确性和有效性，克服单一模型的缺陷，研究者提出了综合集成模型理论，即利用不同方式将具有各类优势的单一模型进行综合集成。常见的综合集成模型有两种方式：第一种是不同模型间组合以获得更优的预测效果，如ARIMA 模型和灰色预测模型通过赋权法进行组合［11］，BPNN、LSTM、ESN 和门回 归单元（Gated Recurrent Unit，GRU）模型的线性组合［12］等；第二种是数据分解后将不同分解模态预测结果集成，主要利用不同分解方法来识别和提取时间序列的内部特征。如Jin 等［13］利用变分模态分解（Variational Mode Decomposition，VMD）对原始数据进行分解，根据平稳性测试结果采用自回归移动平均（AutoRegressive Moving Average，ARMA）模型和核极限学习机（Kernel based Extreme Learning Machine，KELM）模型对不同特征分量进行预测，最后采用KELM 模型非线性集成得到预测结果。梁小珍等［14］使用奇异谱分析（Singular Spectrum Analysis，SSA）对原始数据进行分解重构，依据重构序列的复杂度分别使用粒子群算法和布谷鸟算法双优化的支持向量回归（Particle Swarm Optimization Cuckoo Search algorithm Support Vector Regression，PSOCSSVR）模型和ARIMA 模型进行预测，并线性集成预测结果。此外，常用的数据分解方法还有经 验模态分解（Empirical Mode Decomposition，EMD）［15］、集成经验模态分解（Ensemble EMD，EEMD）［8］等。实验结果表明，采用数据分解方法在降低数据复杂度的同时，也较为明显地改善了模型的预测性能。

近年来，有学者在分解集成思想的基础上提出了二次分解模型，通过组合不同分解方法，将复杂度相对较高的分量进行二次分解，以达到充分提取有用信息、降低预测难度的目的。如梁小珍等［16］采用X12-ARIMA 方法提取了原始数据的季节成分，进而利用改进的自适应噪声互补集成经验模态分 解（Improved Complete EEMD with Adaptive Noise，ICEEMDAN）技术二次分解剩余分量，通过FCM-FTS（Fuzzy C-Means Fuzzy Time Series）模型对各分量序列进行预测，将预测结果线性相加得到最终预测值。然而，已有的二次分解模型大多并未在二次分解后考察分量特征，直接将各个分量进行了相同处理，这可能导致预测模型的选取不合理，从而降低模型预测精度。

综上所述，本文提出了一种新的基于二次分解重构策略的综合集成模型（STL-CEEMDAN-SAAKAB）用于航空客流需求预测。首先，采用STL（Seasonal and Trend decomposition using Loess）分解方法对航空客流量数据进行分解，得到相应的季节分量、趋势分量以及残余分量，再利用自适应噪声互补集成经验模态分解（Complete EEMD with Adaptive Noise，CEEMDAN）对残余分量进一步分解；然后，根据相关特征检验结果，将二次分解后的部分分量与趋势分量相结合，重构得到新的趋势分量，同时将其余分量基于复杂度结果分为低复杂度分量和高复杂度分量；再者，分析不同分量的不同特性，基于模型匹配策略分别采用SARIMA、ARIMA、KELM、双向长短期记忆（Bidirectional LSTM，BiLSTM）网络模型进行预测，其中KELM 和BiLSTM 模型的超参数通过自适应树Parzen 估计（Adaptive Tree of Parzen Estimators，ATPE）算法确定；最后，线性集成得到最终预测结果。

本文的创新和特色之处在于：1）STL 和CEEMDAN 相结合的二次分解策略在充分考虑航空客运量数据季节性特征的同时，还充分挖掘了复杂分量中的有用信息；2）分析二次分解后不同分量的不同特征，合理进行分量重构，同时基于模型匹配策略有针对性地选择预测模型，提升了综合集成模型的预测性能；3）将具有高波动性的残余分量分为低复杂度分量和高复杂度分量，分别采用神经网络模型KELM 和深度学习模型BiLSTM 进行预测，得到更加精确和稳定的预测效果；4）采用ATPE算法对KELM和BiLSTM模型的超参数进行确定。

1 方法与原理

1.1 分解模型

1.1.1 STL模型

STL 是典型的时间序列加性分解方法，该方法相较于传统的季节分解方法（如X12-ARIMA、比率移动平均法等）在处理异常值时具有更强的鲁棒性［17］。对于航空客流数据Yt(t=1，2，…，n)，STL 基于Loess 将原始数据Yt分解为季节成分St、趋势成分Tt和残余成分Rt，其分解表达式如下：

STL 是一种由内循环和外循环两个递归过程组成的迭代方法。每一次内循环分别包含一个更新季节成分的季节性平滑和一个更新趋势成分的趋势平滑。内循环完成后，计算外循环中的鲁棒权值并将其应用于减少外循环对下一个内循环中季节成分和趋势成分更新的影响。在第k+1 次迭代的外循环中，用内循环中得到的趋势成分和季节成分计算残余分量。对于Rt中的任何过大值都被视为异常值，并基于异常值计算一个权值，在下一次内循环的迭代中，权重被用来降低上一次外循环迭代中识别出的异常值的影响。

1.1.2 CEEMDAN模型

EMD 技术作为一种自适应数据分析方法，主要应用于分析非线性和非平稳数据，它可将复杂数据分解为有限个本征模态函数（Intrinsic Mode Function，IMF）。但该方法容易出现模态混淆现象，即在某个IMF 中存在不同模式的信号成分，或者相似模式信号出现在不同IMF 中。为解决此问题，EEMD 方法被提出，该方法在原始数据中加入高斯白噪声，从而缓解模态混淆的问题；但因多次反复加入白噪声会造成最终数据分解成分中包含残留噪声且无法彻底消除，同时新数据序列因加入不同的白噪声在分解过程中可能产生不同数量的分量，导致新的问题生成。为此，CEEMDAN 方法被提出，该方法解决了EEMD 方法中存在的问题，获得了更好的自适应性和收敛性［18］。相较于EMD 和EEMD 方法，CEEMDAN 方法在每次分解时引入惩罚系数ω来控制噪声水平。在逐步分解过程中，CEEMDAN 方法通过M次对剩余分量r(t)和噪声ε(t)重新组合分解的方式，以此来消除噪声的干扰。对于一个原始数据Y(t)，该方法将Y(t)分解为N个IMF 分量和一个残余分量R，表达式如下：

1.2 特征分析

1.2.1 样本熵

样本熵（Sample Entropy，SE）作为近似熵的改进版，是一种用来衡量时间序列复杂度的方法，具有较强的鲁棒性。SE 的核心思想是通过衡量重建后时间序列的子向量之间的距离来测量复杂度，子向量之间的距离越近则时间序列的复杂度越低［19］。对于一个长度为n的时间序列x(t)，首先计算重建子序列对应元素间的绝对值距离，根据距离值来衡量其概率Cm(r)，最终确定x(t)的样本熵值：

其中：m为重建时间序列移动窗口的嵌入维数，本文设定为2；r为宽容度，基于x(t)的标准差SD来确定的，具体为r=0.2 ×SD(x(t))。

1.2.2 最大信息系数

最大信息系数（Maximal Information Coefficient，MIC）用来描述大数据下任意两组随机变量之间的相关程度，它不易受异常值影响，具有普适性和公平性的数据测量特点［20］。如果两 个变量X={xi，i=1，2，…，n} 和Y={yi，i=1，2，…，n}之间存在某种关系，则可作为一个有序集合D=(x，y)，然后将x和y在数据X和Y方向上采取某种方式以网格方式划分，这就可以使得大多数点集中落在单元格里，由此可计算两组变量的MIC 值：

其中：B(n)=nα为样本数n的函数，代表搜索网格的上界，α为一个自定义参数，本文设定为0.6；I(D，X，Y)是在X和Y网格上由D产生的分布的所有最大互信息。如果两组变量X和Y之间相关程度越强，则MIC(D)越趋近于1；反之，越接近0，则说明两变量越有可能为独立变量。

1.3 预测模型

1.3.1 ARIMA模型

ARIMA 是Box 和Jenkins 提出的用于非季节性平稳时间序列数据分析和预测的模型［21］。该模型由自回归项（AR）的阶数p、移动平均项（MA）的阶数q和使时间序列平稳化的差分阶数d组成，可简写为ARIMA(p，d，q)。具体表达式为：

其中：{xi}(i=1，2，…，N)为一个平稳序列，αi为自相关系数，βi为误差项系数，δ为常量，εt为白噪声序列。其中前半部分为AR 项，用来描述当前时间序列数据值与历史时间序列数据值之间的关系，用变量自身的历史数据预测未来值；后半部分为MA 项，主要是通过移动平均法消除预测中的随机波动造成的误差累加。

1.3.2 SARIMA模型

SARIMA 具体包括非季节项ARIMA(p，d，q)和季节项(P，D，Q)s，可简写为SARIMA(p，d，q)(P，D，Q)s。其中季节项的P、D和Q分别代表季节AR 项、季节差分项和季节MA 项，通过对一个s周期的时间序列数据进行季节项分析其季节波动规律［22］。该模型的一般表达式为：

其中：ΦP(Ls)为季节P阶自回归算子、ΘQ(Ls)为季节Q阶移动平均算子，μt为白噪声过程。对于时间序列x(t)，L为后移算子，即Ls=y(t-s)/y(t)。

1.3.3 KELM模型

极限学习机（Extreme Learning Machine，ELM）是快速单隐层前馈神经算法的一种特殊变体，由于输入权值和偏差是随机产生的，因此计算速度很快（如图1 所示）。根据ELM 原则，采用线性方程组的最小二乘法求解Hβ=T可推导为β=H†T，其中H†=HT(HHT)-1是矩阵H的Moore-Penrose 广义逆矩阵。然而，在广义逆矩阵H†中，由于HHT的多重共线性会导致其不是一个非奇异矩阵，这可能造成预测结果不准确的问题。为了克服ELM 的随机输出，提高其泛化性能，提出了一种引入正则化和核函数的方案来改进ELM，即KELM 模型［23］。因此，在优化阶段，可采用正则化系数C获得权重向量β，即：

图1 KELM神经网络结构Fig.1 KELM neural network structure

其中：I代表一个N维的单位矩阵；HHT(i，j)=K(xi，xj)代表ELM 的核矩阵（记为ΩELM），K(·)代表核函数。对于一个给定的训练样本(xi，yi)，其隐含层激活函数为h(x)，则KELM 的输出函数推导为：

其中：核函数K(·)根据不同的训练数据进行调整，常用的有四种核函数，即径向基核函数、线性核函数、多项式核函数和小波核函数。

1.3.4 BiLSTM模型

LSTM 是传统前馈神经网络的一种扩展（如图2 所示）。LSTM 相较于其他循环神经模型最明显的优点是它能够处理消失和爆炸梯度问题［24］。

图2 LSTM单元结构Fig.2 LSTM unit structure

LSTM 通过迭代地从一系列构建块中更新内存状态，从顺序的结构化数据中捕获长期依赖关系。每个构件块都以一个存储单元状态为中心，该状态由通过使用S 型激活函数σ的3 个功能门过滤的循环输入信息进行更新。遗忘门通过遗忘或记忆循环输入控制当前记忆状态的更新，输入门和输出门通过擦除或保持当前单元状态控制循环输入流。BiLSTM 是基于两个LSTM 层开发的（如图3 所示）。

图3 BiLSTM结构Fig.3 BiLSTM structure

BiLSTM 拥有两个可在两个方向上处理数据的LSTM 层，因此能够对来自先前和后续信息进行数据依赖性建模［25］。对于BiLSTM 计算t时刻的输出yt，需要包含前向序列的隐藏状态和向序列的隐藏状态，具体表达式为：

其中：W分别为前向和后向隐藏状态的权重矩阵，b为偏差向量。

1.4 基于二次分解重构策略的航空客流需求预测模型

基于航空客流需求的数据特征以及上述各模型的基本原理，本文提出了一个基于二次分解重构策略的综合集成模型（STL-CEEMDAN-SAAKAB）用于月度航空客流需求的预测。该模型主要包括二次分解及重构阶段和模型匹配预测及集成阶段，基本流程如图4 所示。主要步骤归纳如下。

图4 航空客流需求预测模型Fig.4 Air passenger demand forecasting model

1）二次分解。根据航空客流量数据的季节性特征，采用STL 方法对原始数据进行分解，得到季节分量、趋势分量和残余分量。然后利用CEEMDAN 对残余分量进行二次分解以获得未提取出的有效信息，得到n个具有不同时间尺度特征的IMF 分量（记作IMF1，IMF2，…，IMFn）。

2）基于特征分析的重构。分析二次分解获得的各分量的基本数据特征，根据数据复杂度（SE 值）以及各分量与趋势分量的相关度（MIC 值），选择部分二次分解分量与趋势分量重构为新趋势分量；然后，将剩余分量依据所设定的复杂度阈值重构为低复杂度分量和高复杂度分量。至此，所有二次分解分量重构为季节分量、新趋势分量、低复杂度分量和高复杂度分量四类。

3）模型匹配预测。分析重构后各分量的数据特征，有针对性地选择不同的模型进行预测。具体地，对有明显周期性、数据波动比较规律的季节分量选用SARIMA 模型进行预测；对复杂度低、变化曲线较光滑的新趋势分量采用ARIMA模型来预测；对具有相对较低波动性的低复杂度分量选用神经网络模型KELM 进行预测；而对具有明显非线性非平稳特征的高复杂度分量采用深度学习模型BiLSTM 进行建模与预测。同时，为进一步提高预测精度，本文采用ATPE 算法优化了KELM 和BiLSTM 模型中的超参数，分别记为AK（ATPE-KELM）、AB（ATPE-BiLSTM）。将这一预测步骤简写为SAAKAB（即季节分量SARIMA、新趋势分量ARIMA、低复杂度分量AK、高复杂度分量AB）。

4）集成。最后将季节分量、新趋势分量、低复杂度分量和高复杂度分量的预测结果线性相加，得到航空客流量的最终预测值。

此外，为了衡量模型在多步预测下的表现，本文采用了多输入多输出策略对每个模型(·)进行建模预测，该策略相较于常见的直接策略具有建模任务简单且耗时短的优势［26］。假设一个模型的嵌入维度和零均值的噪声项分别为d和ε，需做h步预测，则预测向量集合(φt+1，φt+2，…，φt+h)，可具体表示为：

2 实验与结果分析

2.1 数据描述

为充分验证本文所提模型的预测性能，本文选取了北京首都国际机场、深圳宝安国际机场和海口美兰国际机场的航空客流量数据作为研究对象进行实证分析。这3 个机场所在城市的地理位置、人口规模、产业结构以及经济状况等均有不同，而且航空客流量数据大小也有一定差异。其中，北京首都国际机场作为我国三大门户复合枢纽之一，航空客流量大，属于特大型机场；深圳宝安国际机场是干线枢纽型机场，航空客流量较大，属于大型机场；海口美兰国际机场为旅游城市机场，受旅游业发展影响较大，航空客流量相对较小。因此，本文选择上述3 个机场的样本数据进行预测可以更客观、系统地评价STL-CEEMDAN-SAAKAB 模型的有效性和稳定性。

本文收集了上述3 个机场2006 年1 月 至2019 年12 月的航空客流需求月度数据（如图5 所示），共计168 个数据，其基本统计描述见表1。此外，按照8∶2 的比例将原始数据划分为训练集和测试集，即2006 年1 月至2017 年2 月设为训练集（共134 个数据），2017 年3 月至2019 年12 月设为测试集（共34 个数据），数据来源于Wind 数据库（www.wind.com.cn）。

图5 3个机场的航空客流需求月度数据Fig.5 Monthly air passenger demand data of three airports

表1 3个机场航空客流需求月度数据的基本统计描述 单位：万人次Tab.1 Basic description statistics of monthly air passenger demand data of three airports unit：104

2.2 评价准则

本文采用均方根误差（Root Mean Square Error，RMSE）、平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）、决定系 数（R2）以及方 向预测精度（Direction Accuracy，DA）作为评价指标从不同角度评估模型的预测性能，具体公式如表2 所示。其中，RMSE、MAPE 越小，表明预测值越接近真实值，模型的预测精度越高；R2越接近1，表明模型的拟合程度越高；DA 越大，表明模型的趋势判断越准确，方向预测精度越高。

表2 评价指标Tab.2 Evaluation indicators

此外，为了进一步比较模型间的差异性，本文从统计视角引入了DM（Diebold Mariano ）检验评价所提模型与基准模型预测精度的差异显著程度。本文以均方误差（Mean Square Error，MSE）作为损失函数，原假设为所提模型的MSE 值不小于基准模型，即提出模型的预测性能低于基准模型。具体的DM 统计量定义如下：

2.3 北京首都国际机场实例

2.3.1 二次分解重构

本文采用STL 分解技术对航空客流量数据进行分解，提取原始时间序列的季节成分和趋势成分，并进一步得到残余成分（如图6（a）所示）。从图6（a）中可以看出，北京首都国际机场客流量数据分解所得的季节分量波动极为规律，反映了航空客流需求在一年内的周期性变化（如每年8 月暑假期间，旅游人数增加，季节分量呈现上升状态）；趋势分量波动平缓，逐年增长趋势明显，反映了在经济增长、行业发展影响下航空客流需求的长期变化情况；残差分量受各类不确定性因素影响较大（如2008 年8 月受北京奥运会影响，残差分量有明显突变），波动情况较为复杂，无明显规律性。

图6 二次分解及重构Fig.6 Dual decomposition and reconstruction

在此基础上，利用CEEMDAN 对残余分量进行二次分解，得到不同振幅和频率的8 个IMF 分量，分别计算各分量的SE 值，分析其复杂度，见图6（b）及表3。可以发现，各分解分量的波动频率依次降低。波动频率越高，该分量的非线性非平稳性越明显，复杂度越高；反之，波动频率越低，该分量的变化趋势越平稳，复杂度越低。进一步，本文分析并计算了各分量与趋势分量的相关度MIC，从表3 的计算结果可知，复杂度越低的分量，对应的MIC 值越大，表明该分量与趋势项的波动状态基本保持一致，说明残余分量中包含了部分未充分提取的趋势变化信息。

表3 二次分解分量的基本特征统计值Tab.3 Basic characteristic statistical values of dual decomposition components

根据各分量基本特征统计值及上述分析，同时考虑分量过多可能造成预测误差的累加及计算成本的增加，本文依据各分量与趋势项的相关度MIC，以及各分量的复杂度SE，将特征相似的分量进行了重构。具体地，将MIC 值大于0.5 且SE 值小于0.1 的分量（即对于CEEMDAN 为IMF8，对于EMD 为IMF7-IMF8）与趋势分量进行重构，作为新的趋势分量。其余分量按照复杂度阈值为0.5 重构为两类，即低复杂度分量（即对于CEEMDAN 为IMF2和IMF5-IMF7，对于EMD 为IMF5-IMF6）和高复杂度分量（即对于CEEMDAN为IMF1和IMF3-IMF4，对于EMD为IMF1-IMF4）。重构后的结果如图6（c）所示。

2.3.2 各模型参数及超参数的确定

在实证分析中，ARIMA、SARIMA 模型参数基于赤池信息准则（Akaike Information Criterion，AIC）最小化准则确定；KELM 模型的核函数及其对应的核参数，以及BiLSTM 模型的学习率（learning rate）、批处理大小（batch size）、隐藏层数（hidden layer size）和隐藏层单元数（hidden size）超参数，均通过ATPE 算法确定。本文对训练集进行5 折交叉验证，根据平均损失值最小原则确定最优超参数。对于KELM 模型，本文最终确定采用线性核函数，图7（a）展示了KELM 模型惩罚参数的确定结果，从图7（a）中可看出随着惩罚参数增大，KELM 模型平均损失值不断减小。BiLSTM 模型超参数确定的结果如图7（b）和图7（c）所示，可以看出当BiLSTM 模型的隐藏层数增加、隐藏层单元数较少以及学习率较低的时候，该模型的平均损失值较低，而批处理大小对模型效果的影响较小。最终，各模型参数及超参数的具体结果见表4。

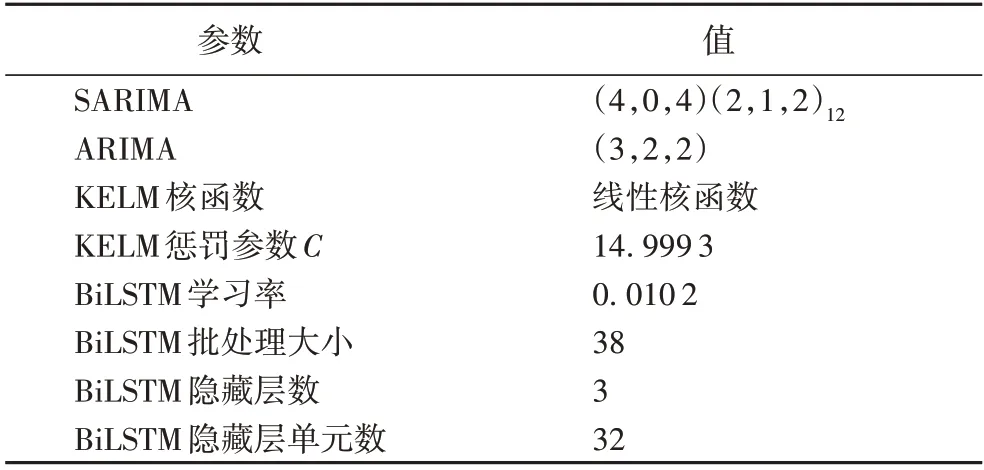
表4 各模型参数及超参数Tab.4 Parameters and hyperparameters of different models

图7 KELM和BiLSTM模型的超参数寻优Fig.7 Hyperparameter optimization of KELM and BiLSTM models

2.3.3 预测结果与对比分析

本文通过替换进行预测前使用的分解策略，设计了单一预测模型、一次分解模型和二次分解重构模型这3 类对比模型，具体如下：1）为验证综合集成模型的优越性，本文选择了综合集成模型中涉及到的4 种单一预测模型进行对比，即ARIMA、SARIMA、AK、AB 模型，均为航空客流需求预测领域中具有代表性的各类预测模型；2）为验证二次分解重构策略和模型匹配策略的有效性，本文在STL 分解结果的基础上，分别选择单一预测模型AK、AB 和模型匹配预测策略（即季节分量SARIMA、趋势分量ARIMA、残余分量AB）设计对比实验，分别记为STL-AK、STL-AB、STL-SAAB；3）基于提出的预测模型，采用EMD 作为二次分解方法，比较不同分解方法的优势，即STL-EMD-SAAKAB 模型。

本文主要采用了RMSE、MAPE、R2和DA 这4 个评价指标，以及DM 检验统计指标对上述各类对比模型的预测结果进行评价。所有模型对北京首都国际机场航空客流量的预测结果具体见表5，提出模型对比其他模型的DM 检验结果见表6。从表5、6 可以发现如下结论。

表5 各模型的1步、2步、3步预测结果（北京首都国际机场）Tab.5 One step，2 step and 3 step ahead prediction results of different models（Beijing Capital International Airport）

表6 各模型1步、2步和3步预测的DM检验结果（北京首都国际机场）Tab.6 DM test results of 1 step，2 step and 3 step ahead prediction of different models（Beijing Capital International Airport）

1）航空客流时序数据具有明显的季节性特征且复杂度较高。对比计量经济模型（ARIMA 和SARIMA 模型）可发现SARIMA 模型预测效果优于ARIMA 模型，这是航空客流数据的季节性特征导致的。对比各单一预测模型的RMSE 值，结合超参数优化算法的深度神经网络AB 模型具有明显的预测精度优势，在多步预测中优于其他所有单一预测模型；且AB模型的拟合精度R2均是最高的，这是因为深度神经网络可较好地捕捉复杂数据内在规律特征。

2）基于STL 的分解集成模型优于单一预测模型。考虑到航空客流需求数据内在受多种特征影响，利用恰当的分解技术处理数据再进行预测可获得预测效果的提升，如STLAK 和STL-AB 的MAPE 值低于所有的单一预测模型。根据STL 分解下各分量的特征采用模型匹配策略可获得更具优势的预测精度和方向精度，如在1 步预测中，STL-SAAB 的MAPE 值 为1.153 6%，DA 值 为0.903 2，均优于STL-AK（MAPE 为2.410 0%，DA 为0.774 2）和STL-AB（MAPE 为1.724 2%，DA 为0.871 0）。

3）二次分解重构集成模型进一步挖掘了航空客流数据中的有效信息且获得了更优的预测性能。在STL 分解的基础上，本文发现残余分量中仍包含有未充分提取的有效信息，因此考虑采用分解技术进一步处理残余分量并重构各分解分量。在多步预测中，STL-EMD-SAAKAB 和STLCEEMDAN-SAAKAB 模型的预测精度和拟合效果均优于其他所有对比模型，且方向精度也均超过0.900 0。从RMSE、MAPE 和R2这3 个误差分析指标来看，STL-CEEMDANSAAKAB 模型在1 步和2 步预测中的效果优于STL-EMDSAAKAB 模型，但在3 步预测中的效果略差。

4）从DM 统计检验角度来看，除STL-EMD-SAAKAB 模型外，本文提出的STL-CEEMDAN-SAAKAB 模型相较于其他对比模型在多步预测中的p 值远远小于0.100 0，也就是说该模型的预测性能在90%的置信水平下明显优于其他对比模型。而基于本文提出预测模型下的STL-EMD-SAAKAB 模型，从统计角度来说有着与STL-CEEMDAN-SAAKAB 模型相近的预测性能。

总的来看，本文提出的STL-CEEMDAN-SAAKAB 模型，综合了二次分解重构策略和模型匹配策略的优势，在对北京首都国际机场航空客流量的预测中，相较于其他模型，无论从预测精度、方向精度和拟合效果还是从统计分析角度来看，都有着较优的预测性能。

2.4 其他机场实例

为了更加全面、充分地评估所提模型的预测准确性和有效性，进一步选择客流量数据量级不同、特点不同的两个机场（深圳宝安国际机场和海口美兰国际机场）进行建模预测，在实证分析中，模型参数的确定方法、重构依据以及对比模型的设置均与上文保持一致。两个机场训练集误差评价结果和DM统计检验值分别见表7、8和表9、10。

表7 各模型的1步、2步、3步预测结果（深圳宝安国际机场）Tab.7 One step，2 step and 3 step ahead prediction results of different models（Shenzhen Bao’an International Airport）

表8 各模型1步、2步和3步预测的DM检验结果（深圳宝安国际机场）Tab.8 DM test results of 1 step，2 step and 3 step ahead prediction of different models（Shenzhen Bao’an International Airport）

表9 各模型的1步、2步、3步预测结果（海口美兰国际机场）Tab.9 One step，2 step and 3 step ahead prediction results of different models（Haikou Meilan International Airport）

从预测评价结果来看，本文所提的STL-CEEMDANSAAKAB 模型的总体效果优于其他对比模型。在深圳宝安国际机场航空客流量的多步预测中，本文模型的拟合效果R2值均在0.98 以上，方向精度均为93.55%；而在海口美兰国际机场的多步预测中，本文模型的RMSE、MAPE值均为最低，且R2值为最高，甚至在1、2步预测中方向精度DA值达到了100%。

表10 各模型1步、2步和3步预测的DM检验结果（海口美兰国际机场）Tab.10 DM test results of 1 step，2 step and 3 step ahead prediction of different models（Haikou Meilan International Airport）

从DM 统计检验角度来看，除了STL-EMD-SAAKAB 模型外，本文模型在深圳宝安国际机场航空客流量预测中，预测性能在95%的置信水平下明显优于其他对比模型；而在海口美兰国际机场航空客流量预测中，本文模型相较于其他对比模型在多步预测中DM 统计值的p 值远远小于0.100 0。值得注意的是，上述两个机场在单一预测模型对比中，可发现SARIMA 模型的预测效果是最优的，这说明深圳宝安国际机场和海口美兰国际机场的航空客流量受季节影响较为明显，季节性特征为主导因素，而其他不确定因素影响相比北京首都国际机场较低。其余结论均与北京首都国际机场实例中得到的一致，体现出本文提出的预测模型的有效性与优越性。

3 结语

在当前国民经济稳步增长、航空运输业快速发展的背景下，航空客流需求不断增长，给相关管理工作带来了新的挑战。如何准确预测航空客流需求，对实现航空运输资源的优化配置，提升航空运输能力和质量，都显得尤为重要。为此，本文从数据特征驱动角度出发，以“分而治之”思想为指导，构建了一个航空客流需求预测的综合集成模型。该模型考虑了航空客流量数据的内在发展规律，挖掘了需求序列的季节性特征和趋势变化情况，采用二次分解重构策略处理非线性非平稳的残余分量数据，进而利用模型匹配策略依据数据复杂度有针对性地选择合适的预测模型，集成得到最终预测结果。北京首都国际机场、深圳宝安国际机场以及海口美兰国际机场的实验结果表明，STL-CEEMDAN-SAAKAB 模型预测效果突出且稳定，所提出的二次分解重构策略和模型匹配策略是有效的航空客流需求分析和预测方法，对航空客运业的发展甚至其他研究领域都有借鉴意义。虽然，通过结合神经网络模型预测得到了较高的预测精度，但预测结果缺乏一定的可解释性，后续工作将尝试融合多源数据，进行特征提取以此来获得具有可解释性的预测模型。