基于用户潜在状态及依赖关系学习的时序行为推荐

温 雯，梁方宇

（广东工业大学 计算机学院，广州 510006）

0 引言

挖掘用户的偏好和兴趣，并帮助用户从海量数据中发现所需要的信息是推荐系统的主要目标。传统的推荐算法主要从用户历史数据中捕捉个体偏好［1］，进而实现个性化推荐。然而，线上用户行为往往随时间而变化，同时各阶段偏好的依赖关系也颇为复杂。例如，某个用户在过去一个星期的每天上午都喜欢看财经新闻，而晚上的时候会选择观看音乐节目，体现出用户在不同时间段的偏好不同；又或者是某个用户下午去了花店，接下来晚上用户选择了西餐厅，体现出用户在不同时间段的偏好存在某种依赖关系。

对用户的时序行为进行建模并有效捕捉用户各个阶段偏好的变化模式［2-4］，对于提高个性化推荐的灵活性和有效性具有重要的现实意义。推荐领域中基于协同过滤的主流算法有因子模型（Factor Model）［5-6］、Item2Vec 模型［7］。它们通过矩阵分解或者表征学习的方法获得用户及物品的低维表示，进而使用这些低维向量来表示用户的兴趣偏好和物品的代表特征，以实现个性化推荐；同样是基于协同过滤的算法 Mult-VAE（Variational AutoEncoder with Multinomial likelihood）［8］则是利 用变分 自动编 码（Variational AutoEncoder，VAE）学习用户隐式反馈数据。然而此类算法无法直接刻画动态变化的用户偏好，也不能捕捉时序行为之间的依赖关系，因而需要针对时序推荐任务设计特定的算法，现有的相关研究工作主要从两个角度展开。一类是将时间作为一项特征对已有的推荐算法进行改进，如文献［9］中的timeSVD++（time-aware Singular Value Decomposition）算法，在用户（项目）特征中直接加入时间特征，在事件（项目）空间很大的情况下，此类算法首先面临单一时间片中行为高度稀疏的问题，其次该算法依然未对时序行为之间的依赖关系进行有效建模。另一类算法则是直接建模和学习时序行为的转移概率，如文献［10-11］通过将行为序列建模为一阶马尔可夫链来学习用户行为的动态性；但此类方法主要对行为序列中项与项的转移进行建模，没有考虑时间信号，也没有考虑到用户行为在时间维度上更加复杂的依赖关系。

为了解决前述时序推荐中单一时间片行为稀疏以及行为依赖关系复杂的关键难题，本文从动态系统的角度，假设用户的时序行为由不同阶段的不同状态产生，从而将用户时序偏好的发现转化为时序状态的动态变化及依赖关系学习问题。通过对时序状态的低维表示，解决行为稀疏的问题；并通过建模状态之间的图网络，实现复杂依赖关系的捕捉。具体而言，首先利用最大池化层级结构对每一时间段的用户-物品交互行为进行特征提取，获得每一时间段的潜在状态的低维表征；进而将各时间段的潜在状态输入到特定的图神经网络以学习用户的潜在状态在时序上的依赖关系，从而捕捉用户偏好的动态变化。

本文的主要工作如下：

1）提出了一种基于潜在状态表征的时序推荐算法。根据时间段划分用户对物品的时序行为，然后学习用户在每个时间段的潜在状态。

2）提出了能够学习用户不同时间段潜在状态的依赖关系的图神经网络模型，捕捉用户潜在状态的变化规律，从而实现用户不同时间段的个性化推荐。

3）将所提算法在多个的真实数据集进行了实验，结果表明算法能有效提高时序推荐的性能，在各项评估指标上都能表现得更好。

1 相关工作

近年来，研究学者们提出了许多针对时序数据的状态表示学习的算法以及基于时序行为的推荐算法，因此本章将回顾这两类算法的最新工作。

1.1 状态表示学习

针对时序数据时间动态性建模的一类重要算法是基于学习序列数据的低维状态表示。例如，基于因子分解的个性化马尔可夫链（Factorizing Personalized Markov Chain，FPMC）［10-11］通过将行为序列建模为一阶马尔可夫链来学习用户行为的动态性，并通过分解转移矩阵来学习序列状态表示。基于深度学习的状态表示算法，例如文献［12］中提出了门控循环单元（Gate Recurrent Unit，GRU）学习序列数据的表示；文献［13-14］中提出了深度状态空间模型（Deep State space model，DeepState）从时间序列的连续实值中学习序列模式，但不能直接适用于用户行为，因为用户序列行为是由高维离散事件组合而成的。文献［15］中提出了结构化世界模型的对比学习（Contrastively-trained Structured World Models，C-SWMs）算法，从复杂关系的顺序数据中学习模式，模拟和捕捉多个对象之间的相互作用，同样与用户行为的设定不同。C-SWMs 的灵活性启示本文，图神经网络是建模每一个时间段的潜在状态依赖结构的可行的方案。

1.2 时序推荐

近年来，基于时序行为的推荐算法开始受到研究人员的关注。研究学者们提出了许多有效的算法捕捉用户行为的动态性，主要可以分为以下两类。

第一类算法通常考虑的是用户行为序列，但只包括了行为的时间先后顺序信息。这类算法一般会假设下一个点击行为依赖于历史的点击行为。例如文献［12］中提出使用门控循环神经网络学习行为序列的表示，使用序列的表示来预测下一个交互的项目；文献［16］中提出利用卷积核来捕捉时序模式；文献［17］中提出的分层门控网络（Hierarchical Gating Network，HGN）则是通过多层门控模块捕捉用户过去访问的项目与用户将来访问的项目之间的关系；文献［18］中提出了一种基于个性化物品频率的K最近邻（K-Nearest Neighbors，KNN）算法来学习下一个篮子推荐的时序模式。这类算法从稀疏的时序行为能够同时捕捉用户的长期偏好和短期兴趣，然而却忽略了时间相关的信号。另一种算法利用时序行为来辅助学习特征向量，例如文献［19］中提出基于词向量模型对用户视频播放序列建模，再对用户的播放历史进行视频聚类获取用户的偏好；文献［20］中利用时间先后信息构建了用户（产品）消费网络，结合最近邻和矩阵分解模型学习用户和产品的特征向量。

第二类算法则会假设用户（物品）的动态性与时间信息有关。一种代表性算法是直接将时间信息作为特征学习，例如文献［9］中提出的timeSVD++算法；文献［21］中提出动态兴趣模型来捕捉用户偏好的时间动态性；文献［22］中通过映射时间特征到不同细粒度的区间得到类别特征。另一种算法将时间看成一个不同的维度，例如文献［23］中把每段时间的用户-物品交互矩阵分解得到的特征矩阵作为输入，然后基于时序模型预测出未来时间段的特征矩阵；文献［24］中发现两种用户行为的时间模式，包括用户可能在特定时间对特定商品发生交互以及两个相关行为的时间间隔模式，通过捕捉这两种行为模式来建模用户的动态偏好。

本文受文献［24］中绝对时间模式（Absolute Time Pattern）启发，假设用户在特定的时间段会有特定的潜在状态，且用户在特定时间段的行为依赖于该潜在状态；同时利用文献［25］中提到的最大池化操作作为潜在状态学习算法，考虑到这两类算法都没有显式地建模时序行为之间的依赖关系，本文提出使用图神经网络来建模潜在状态之间的依赖关系并学习用户潜在状态的变化。

2 问题定义

本文将给定用户的历史数据构建成带时间戳的高维事件序列，可以表示成时间线，其中：ti表示时间戳，ei可以表示事件或者物品，ε为事件集合或者物品集合。进一步将一个“时期”划分为固定间隔的“时段”，本文设定每个“时期”有τ个“时段”。本文中一个“时段”可以是一个小时、一天或一个月；相对应的一个“时期”可以是一天、一个星期或一年。为方便起见，在下文中本文使用用户-物品交互矩阵Xt∈Ζτ× ||ε来表示第t个时期的物品交互集合，其中Xt(j，：)=是第t个时期中第j个时段的用户-物品交互向量。

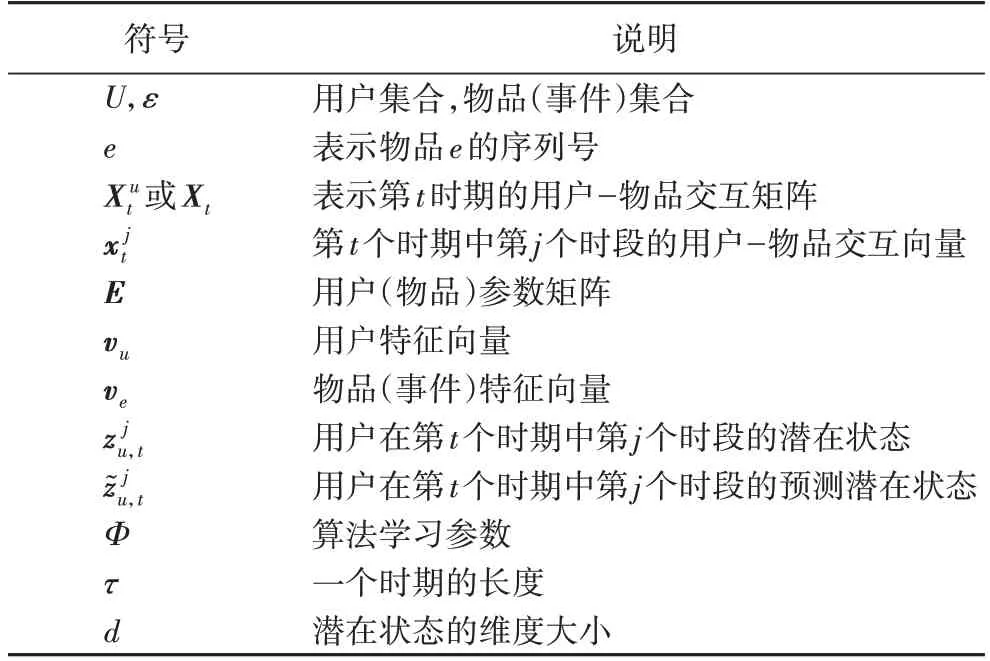
表1 符号描述Tab.1 Description of symbols

3 基于潜在状态学习的推荐策略

本文算法的关键思想是学习用户时序行为的潜在状态依赖关系。因此，首先根据时间段划分用户对物品的时序行为；然后利用两层的最大池化操作学习用户在每个时间段的潜在状态；接着输入用户在不同时间段的潜在状态到图神经网络学习依赖关系；最后预测出用户在下一时期的潜在状态，并生成推荐列表。这是一个端到端的算法，完整流程见3.5 节。

3.1 潜在状态表示学习

本文将用户的特征向量表示成vu，将物品或者事件的特征向量表示成ve，其中vu，ve∈Rd，d表示向量的长度。这些向量是模型需要学习的参数。因此，本文定义模型的用户（物品）参数矩阵，称之为向量查找表：

其中：用户数量N=|U|，物品数量M=|ε|。模型使用高斯分布来随机初始化向量查找表。

基于潜在状态学习的推荐算法首先需要找到一个映射f：X→Z，其中∈X，∈Z，将高维的事件域映射到低维的潜在状态域，也就是学习用户的潜在状态特征。在文献［2，16］的启发下，算法设计该映射函数是一个层级结构（式（3）），用来表示用户在每个时段的潜在状态。

结合输入的用户-物品交互矩阵X，通过查向量查找表（Ee）的方式构建用户u在第t-1 时期的每个时段的物品特征矩阵，其中=1；j=1，2，…，τ。得到用户在每个时段到潜在状态的映射函数：第1 层从构建好的物品特征矩阵提取特征（f1）；第2 层构建用户在当前时段的状态特征向量（f2）。具体的公式定义如下：

其中：v[d] ∈R 表示特征向量第d维度的值，V∈Rd×k，|V|=k。最大池化函数可以选取每个维度权重更大的特征作为下一层的输入。

关于潜在状态表示学习的层级结构（式（3））的理解为：第一层最大池化函数聚合了用户在每个时期的物品特征；第二层的最大池化函数聚合了用户长期的特征向量和当前时段的物品特征。

3.2 依赖关系学习

本文使用一个图来表示用户的潜在状态在时序上的依赖关系，图的τ个节点表示τ个时段的潜在状态，图G上相连的两个节点相互依赖。因此，本文设计了一个图神经网络（Graph Neural Network，GNN）来学习τ个时段的潜在状态的依赖关系以及潜在状态的变化规律。图神经网络的输入为上个时期t-1 的τ个时段的潜在状态（式（3））：

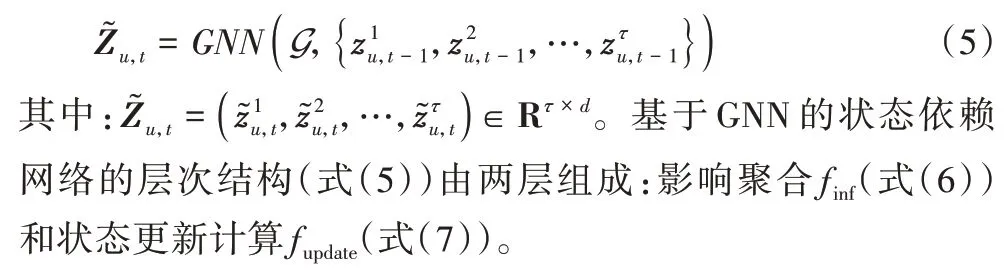
影响聚合（Influence aggregation）为了汇总每个时段的邻居的依赖信息，实现了一个全连接层finf来学习不同邻居的“依赖影响”，汇总得到的依赖权重用表示，如下：

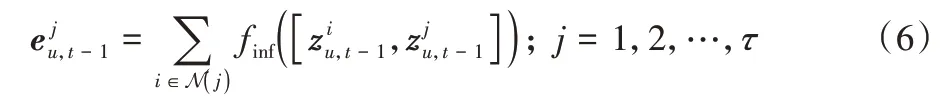
其中：N(j)表示与节点j有一阶边的节点集合，[，]表示向量拼接操作。

状态更新计算（State-update calculation）本文假设时段的潜在状态的更新依赖于其他邻居状态依赖信息的传播，因此结合上一个时期t-1 的潜在状态信息和式（6）得到的依赖权重，预测下一时期潜在状态

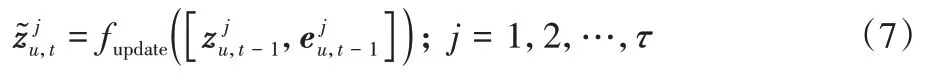
finf（式（6））和fupdate（式（7））以非线性全连接网络的形式实现，使用的激活函数是ReLU 函数；因此算法需要学习这两个全连接网络的参数，同时激活函数的引入可以增加模型非线性的表达能力。结合式（7），具体的潜在状态更新形式化如下：

3.3 预测与训练损失

对于给定用户u和上一个时期的观察数据，通过式（8）预测出。因此，基于softmax 函数本文定义了兴趣概率分布如下：

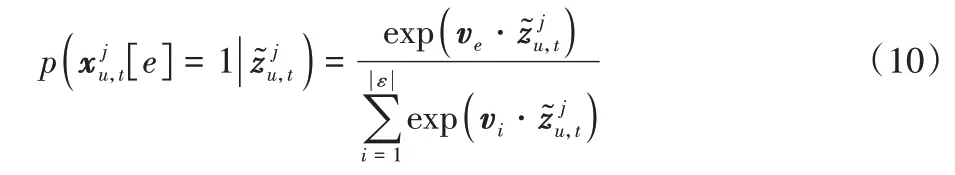
假设用户点击概率服从多项式分布，因此对于给定训练样本，可以得到关于用户u的第t个时期的对数似然估计定义如下：

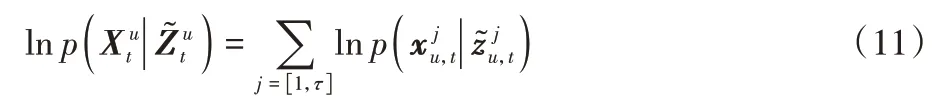
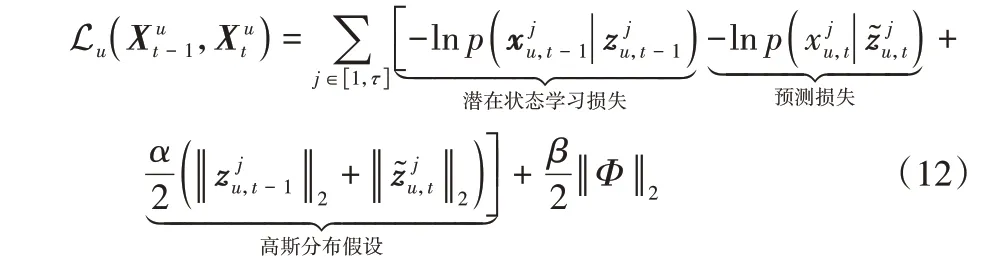
3.4 生成推荐列表

基于潜在状态学习的时序行为推荐根据上一时期的历史交互，预测出下一个时期用户的潜在状态；然后利用式（10）计算用户对物品的兴趣偏好，按照用户对物品的兴趣度降序排列，取top-R生成推荐列表。

3.5 算法流程及时间复杂度分析

本节给出完整的模型学习算法流程以及算法的时间复杂度分析。算法流程如算法1 所示。

算法1 模型学习算法流程。

分析算法1 得出，算法学习是迭代训练的过程，训练一次的时间消耗在算法1 的步骤3）～10），步骤5）只涉及两层的最大池化操作属于Ο(n)的时间复杂度，步骤6）的神经网络前向传播时间复杂度为Ο(n)，步骤9）的时间复杂度与算法的参数空间有关。分析得出算法的参数空间包括向量查找 表(|U|+|ε|) ×d，图神经 网络参 数n1× 2d2+n2×d2+n3×d，假设了算法具有n1层d×d网络结构，依此类推。

4 实验与结果分析

4.1 实验设置

4.1.1 实验数据

实验使用了Foursquare 数据集［3］（也可以描述成兴趣点（Point Of Interest，POI）数据集）和节目点播（Internet Protocol Television，IPTV）数据集。Foursquare 数据集包括了两个分别在纽约（New York City，NYC）和东京（ToKYo，TKY）收集的10 个月签到数据，每条签到数据包含时间戳、签到地点id和用户id。节目点播数据集是一个真实数据集，包括了一个月的用户观看电视节目记录，每条记录包含了用户id、时间戳和电视节目id。对于NYC 和TKY，“时段”是一天，“时期”是一周；对于IPTV，“时段”是一个小时，“时期”是一天。对于不同的数据集，算法的训练输入只使用了时间戳前面的历史数据，并且使用每个用户划分时间戳后面的互动记录进行评估指标的计算。关于数据集详细的统计数据见表2。

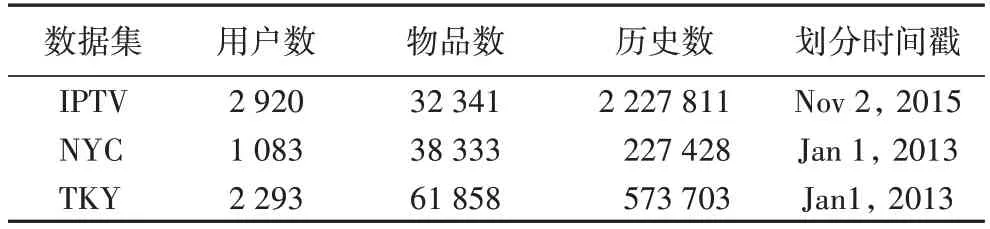
表2 实验中使用的数据集的统计数据Tab.2 Statistics of datasets used in experiments

4.1.2 基线算法

为了验证本文算法的有效性，将本文算法和目前主流的推荐算法在3 个数据集上进行对比。所选择的基线有传统的协同过滤推荐算法，如：基于协同过滤的Mult-VAE 算法没有考虑到用户偏好的动态性，为了适应本文的任务，应用Mult-VAE 学习每个时间段用户偏好表示；分层表示模型（Hierarchical Representation Model，HRM）的层级结构与本文的潜在状态表示学习模块高度相关，但没有捕捉潜在状态在时间线上的依赖性；Caser、HGN 和TIFU-KNN（Temporal Item Frequency based User-KNN）是近期主流的时序推荐算法，它们从不同角度捕捉用户行为的顺序模式。对于上述的基线算法，下面进行简单的描述：

1）Mult-VAE［8］。基于协同过滤的算法，结合了多项式似然对变分自动编码器进行拓展。

2）HRM［25］。该算法结构包含两个最大池化层，同时捕捉用户的顺序模式和一般偏好。

3）Caser［16］。该算法将连续事件构造成类似文本的连续句子，并将其输入到卷积层，以便捕捉连续的模式。

4）HGN［17］。该算法利用分层门控网络来学习项目的潜在特征，然后计算项目与项目的相似度来衡量项目之间的关系。

5）TIFU-KNN［18］。一种基于KNN 的算法，考虑了个性化物品频率信息中的重复消费模式和协同过滤信号。

4.1.3 实现细节

如本文3.1 节所述，本文算法使用了用户（物品）参数矩阵以及潜在状态，其中IPTV 的用户（物品）的特征向量和潜在状态的维度设置为100，NYC 和TKY 数据集设置为50。学习批量大小设置为8，Dropout 率和Adam 优化器的学习率分别设置为0.1 和0.001。超参数α和β设置见4.2.3 节。算法基于PyTorch1.3.1 版本深度框架实现，并在GeForce RTX 2080 Ti GPUs 的机器上训练。

4.1.4 评估指标

实验使用3 个基于排序的评估指标：平均精度均值（Mean Average Precision，MAP@R）、召回率（Recall，Recall@R）和归一化折损累计增益（Normalized Discounted Cumulative Gain，NDCG@R）。评估指标在本文的具体定义如下。

平均精度（Average Precision，AP）是指用户实际交互过的物品数出现在推荐列表中的比例，平均精度均值则是对每个用户计算出来的平均精度求平均，计算公式如下：

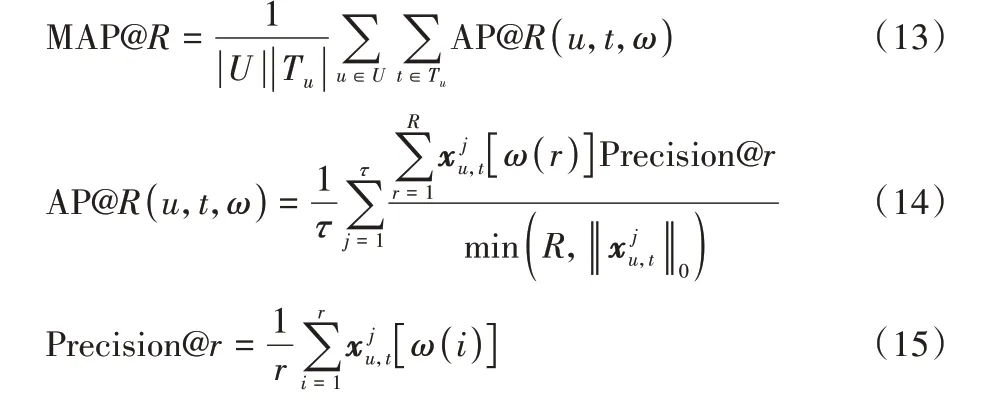
其中：ω(r)是指推荐列表第r个物品的序列号是指用户-物品交互观测向量，[·]是指向量取值操作。

召回率（Recall@R）是指推荐列表中用户实际交互过的物品数与用户实际交互物品总数的比例，其计算公式如下：

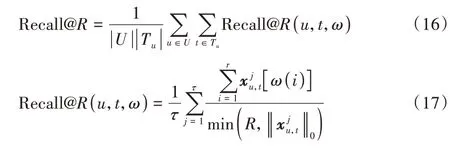
归一化折损累计增益是衡量推荐列表的排名质量，用户实际交互的物品在推荐列表排名越靠前，增益越大，其计算公式如下：

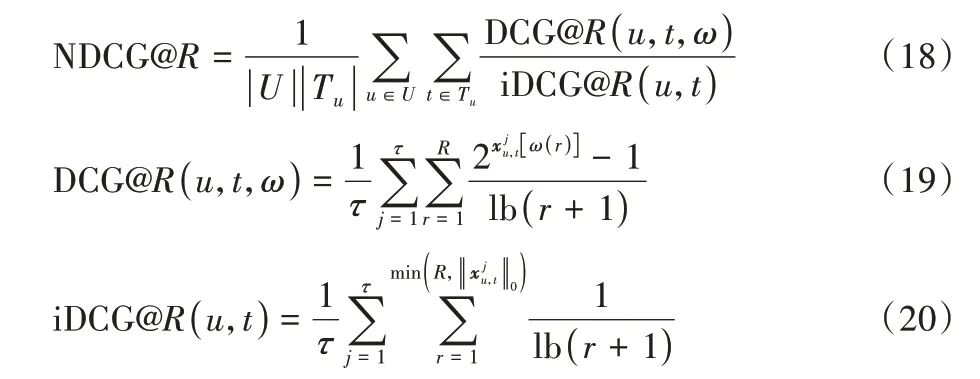
4.2 实验分析

对本文算法进行性能分析实验，主要从3 个方面开展：基线算法对比、状态依赖消除和参数敏感性分析。

4.2.1 基线算法对比实验

为了验证本文算法的有效性，将提出的算法和目前主流的几类推荐算法在IPTV、NYC 和TKY 这3 个数据集上进行了对比。详细的实验结果见表3，最后一行表示本文算法相比表现最好的基线算法（横线）提高的比率。

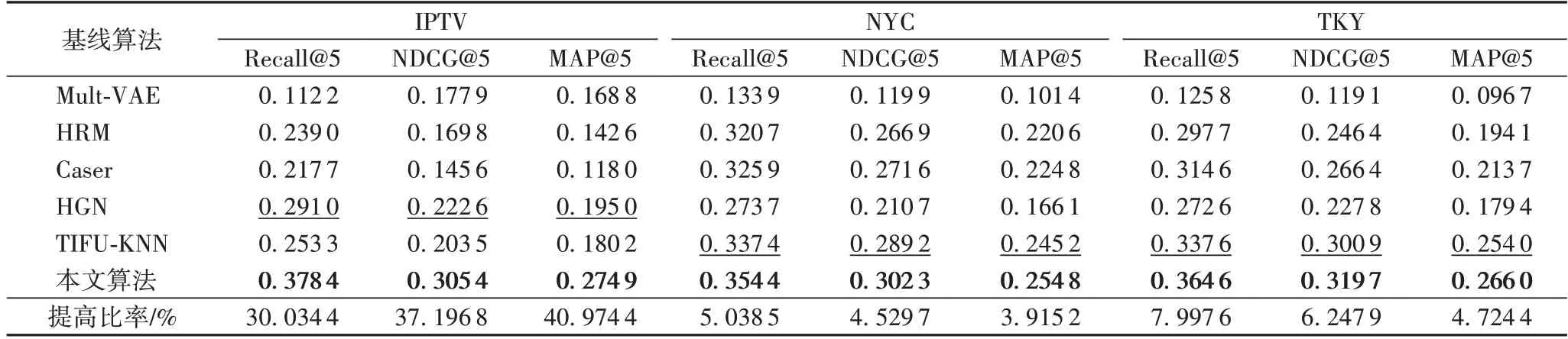
表3 与基线算法的性能比较Tab.3 Performance comparison with baseline algorithms

本文算法在3 个数据集的评估指标Recall@5、NDCG@5、MAP@5 上，与较好的HGN 算法、TIFU-KNN 算法相比均有所提高。此外，根据表3 实验结果，可以获得以下结论：

1）Mult-VAE 没有考虑到用户的偏好是动态变化的，所以与捕捉用户行为的动态性的算法（HRM、Caser、HGN、TIFU-KNN）相比，效果表现不理想。

2）本文算法与下一个项目推荐算法（Caser、HGN）和下一个篮子推荐算法（HRM、TIFU-KNN）相比，效果都要表现得更优，特别是在表3 的MAP@5（0.274 9）上，相较于性能最好的基线算法HGN（0.195 0）提高了40.97%，说明通过图神经网络捕捉时间线上潜在状态之间的依赖关系和学习用户的动态潜在状态的算法在本文任务的优越性。

3）相较于IPTV 数据集，本文算法在另外两个数据集上的性能与性能最好的基线算法TIFU-KNN 相比提升幅度不明显，可能是因为所提算法受到了数据集的噪声影响，潜在状态依赖模式没有那么明显，或者潜在状态的依赖关系更加复杂。

4.2.2 状态依赖消融实验

本文所提的潜在状态依赖学习在本文算法中起到最重要的作用。为了探究3.1 节描述的潜在状态依赖学习对下一个时期推荐的贡献，本节在NYC、TKY、IPTV 数据集上设计了状态依赖消融实验。实验结果分别如图1 所示。

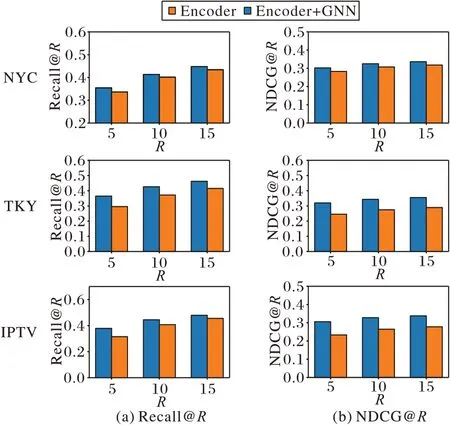
图1 消融实验结果Fig.1 Results of ablation experiments

在本节实验，去掉潜在状态依赖的模型等价于去掉算法1 的步骤6），保留了式（2）～（4）计算用户潜在状态。从图1 可以看出，本文算法引入了潜在状态依赖学习在3 个数据集上都能提升其性能，其中IPTV 和TKY 数据集上的性能提升较为明显，3 个数据集表现的差异性也在4.2.1 节作了简单的分析。实验结果表明，潜在状态依赖学习的引入可以有效提高对下一个时期推荐的性能。

4.2.3 参数敏感性分析

为了验证超参数对算法性能的影响，本文对算法的高斯分布假设的权重α和参数正则化的权重β进行了敏感性分析。

图2（a）说明了算法在不同的权重α下的性能比较稳定。由图2（a）可知：当α≤0.4 时，算法性能会有所下降；当0.5 ≤α≤1 时，算法性能会比较稳定。图2（b）表明了参数正则化不同的权重对算法评估指标的影响，可以发现：当β＞0.6 时，算法性能会明显下降；当0 ≤β≤0.6 时，算法的性能比较稳定。以上说明α和β可以在一定程度上调节算法的性能，但算法对这两个超参数在合适的范围内不会太过敏感。因此本文将参数设定范围在0 ≤α≤1，0 ≤β≤2，然后通过网格搜索方式确定α和β在不同数据集的最优参数组合。

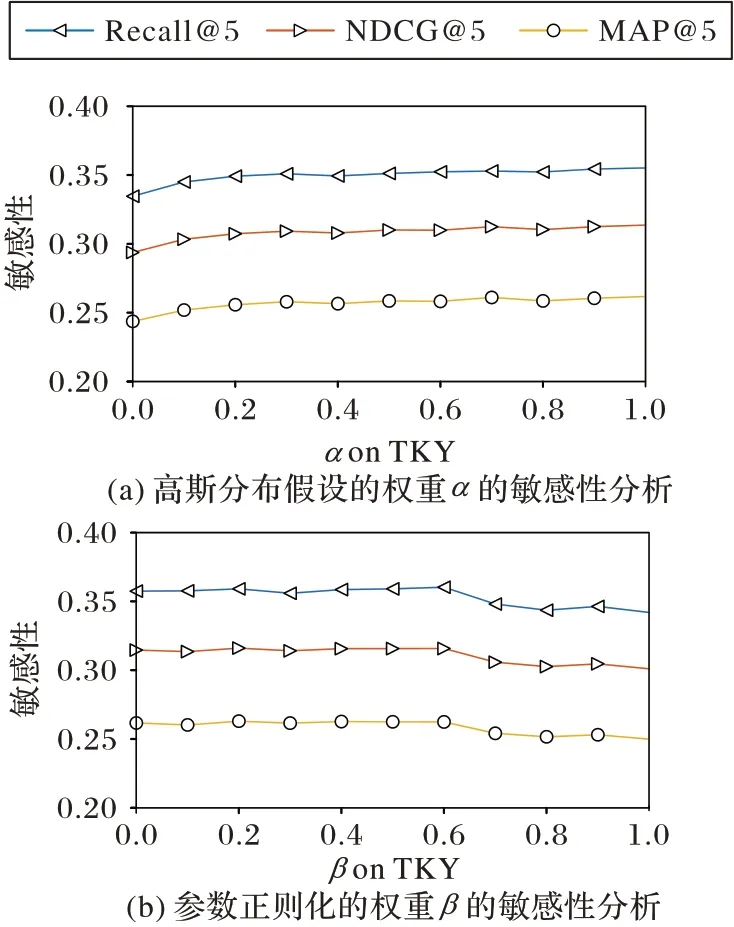
图2 超参数的敏感性分析Fig.2 Sensitivity analysis of hyperparameters

5 结语

本文提出了一种基于潜在状态的时序推荐算法，利用潜在状态依赖关系提高系统个性化推荐能力。该算法通过最大池化函数学习时序行为在不同时段的潜在状态，并使用图神经网络对潜在状态进行更新和有监督训练。实验结果表明，该算法在时序推荐预测任务中比目前主流的时序推荐算法的表现更好；而且本文对于基于潜在状态的时序推荐工作提供了一个新的思路，即可以探索隐藏在时序行为的潜在状态，并利用图神经网络工具学习用户偏好的变化规律。本文接下来的工作将考虑引入动态的网络结构和更好的潜在状态学习算法，使算法能更有效地捕捉复杂的潜在状态依赖关系。