一致性视角下数学知识内容和学习轨迹初探

摘要 《义务教育课程方案和课程标准(2022年版)》的核心关键词之一是一致性。数学教师要在一致性的視角下重新审视知识内容和学习过程。数学知识内在的一致性可以从跨领域、领域内、单元内三个不同维度进行分析。一致性基础上的数学内容指向一致性的数学学习过程:不同领域知识学习采用大概念统领整合的方式;领域内知识学习采用问题串引领递进的方式;单元内知识学习采用结构化学材贯通化归的方式。
关 键 词 《义务教育课程方案和课程标准(2022年版)》 一致性视角 知识内容 大概念问题串结构化学材
引用格式 孙谦.一致性视角下数学知识内容和学习轨迹初探[J].教学与管理,2022(35):34-37.
《义务教育课程方案和课程标准(2022年版)》(以下简称 《标准》)中,数学课程内容和目标的描述强调整体性和一致性。数学课程内容指向同一个目标——以“三会”(会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界)统领,通过数学学习让学生获得基于知识内容学习的“四基”(基本知识、基本技能、基本思想和基本活动经验)、基于问题解决的“四能”(发现问题的能力、提出问题的能力、分析问题的能力和解决问题的能力),并在学习过程中形成正确的情感、态度和价值观。在总目标统领下的学段目标是总目标在各个学段的具体体现,是依据不同学段学生的发展特征,将总目标进行分解而产生的。这种分解是“三会” “四基”和“四能”的具体化,基于不同学段的内容要求,融入核心素养的具体表现,详细描述了每个学段达到的不同层次、不同水平的要求,为具体学习内容的设置和选择、教学活动的组织和开展、学习评价的设计和实施,提供具体、可操作的标准。课程目标的一致性决定了课程实施过程中,教师必须具备一致性视角——一致性视角下的小学数学学习,就要把数学知识、数学学习都看作具有内在一致性的整体结构。
一、小学数学知识内容的内在一致性
1.不同领域知识之间的一致性
义务教育阶段的小学数学知识分为 “数与代数”“图形与几何”“统计与概率”和“综合与实践”四个领域,不同领域之间包含的具体内容虽不相同,但都指向培养学生核心素养的共同目标。目标的实现以知识内容为载体,所以每个领域知识内容的组织和安排也存在着一致性。当下的小学数学教学目标,主要围绕知识技能、数学思考、问题解决和情感态度四个核心元素进行阐述。知识技能主要包括数学概念性知识和数学方法性知识。数学思考主要围绕数感、符号意识、空间观念、几何直观、运算能力、数据分析观念和推理能力等若干核心素养展开阐述[1]。问题解决主要强调解决问题的步骤——数学表达、应用解释和评估。而情感态度则没有固定的程式过程,它弥散在学习过程的始终。结合不同版本小学数学教材的对比分析,发现这些核心元素呈现如下关系(如图1):以问题解决为核心和最终指向,关联所需要的数学概念(数,代数,几何,统计等)、数学技能(数和代数的计算、空间知觉和数据分析等)和数学思考(分类、对比和推理等规则),在学习的过程中始终伴随着科学和理性精神(反思、批判等元认知)的发展,并使情感、态度得到升华。
2.领域内知识之间的一致性
每个学段的学习内容都涉及四个知识领域,其中“综合与实践”与其他三个领域略有不同,主要体现为跨学科的综合性,所以承载的知识点不明显。其他三个领域的数学知识都有明确的知识点分布,并采用螺旋上升的方式编排,多层次、循环式深入,后续学习都在先前基础上进行,某个领域内的知识呈现都遵循相对统一的顺序(如图2)。首先,数学概念性知识是数学知识体系的基本元素,是分析和解决问题、发展抽象思维的基础,包含概念内涵和外延两个方面的知识;接着,在此基础上发展数学方法性知识,也就是将概念作为对象进行各种操作,形成相关的规则知识和模型认识等;最后,是对前面所学进行综合性应用,强调将概念、规则和模型作为工具和方法,在具体情境中应用并解决问题,包括本领域内部知识的综合应用以及跨领域知识的综合应用。
3.单元内知识点之间的一致性
一个单元聚焦一个主题,内含诸多知识点,这些知识点的呈现也存在着一致性,主要体现在三个方面。
(1)情境主题的一致性。同一单元使用同一个主题情境贯穿一个单元的若干个知识点,反映同一情境的多个方面。例如苏教版《数学》二年级上册“100以内的加法和减法(三)”,所有的例题都呈现了儿童室内手工活动的场景(折纸船、做纸花和串珠);五年级上册小数加减法单元,所有的例题使用的都是生活中的购物情境。
(2)工具支架的一致性。围绕学习主题,使用较为统一的、适合儿童思维发展的数学支架。例如认识万以内的自然数时,使用计数器和可拼搭方块工具直观呈现数的组成和数位;4~9的乘法口诀,都用表格工具呈现某一个数乘1、2、3、4……的得数。
(3)步骤程序的一致性。小学数学中规律、规则的推导经常采用不完全归纳法,具有类似的步骤与程序,同一单元内的知识点因其关联紧密,所以更加注重程序的统一。例如,五年级上册第一单元多边形的面积中,平行四边形、三角形和梯形的面积知识都是采用这样的学习步骤:利用方格图求特例图形(直角三角形)的面积→剪拼操作求一般图形(直角三角形、锐角三角形和钝角三角形)的面积→文字或符号归纳总结公式→应用公式解决简单实际问题。
由以上分析可以看出,小学数学知识是有组织的整体知识,它是围绕某个主题或者按照一定的关系组织起来的整块知识。但是,有组织的知识内容或结构性要素并不能支撑起深度学习的发生。因为如果数学学习只是学习知识本身,或读写算等浅层次能力,那么获得的都将是“静态”的、 “惰性”的知识,不能灵活运用于生活,更无法自主创新知识,适应未来发展的需要。深度学习之“深”实为“知识运用”,它依赖于个人与知识的交互过程,聚焦于如何将所学知识应用在新的学习环境或者情境解决问题,也就是如何“迁移”[2]。在具体的数学教学活动中要让学生在具身性、情境性和非结构性的生活情境中,探索“如何做、如何运用”的有效路径,一方面,强化学科的结构性,不断彰显知识背后的逻辑和意义价值;一方面消解知识的结构性,增强知识的开放性、具身性和默会性[3]。这种将知识结构和知识运用相互转化,融合一致的学习过程才能将惰性的知识变成灵活的能力,发展个体综合素养,体现学科育人价值。
二、小学数学学习过程的一致性实践路径
1.不同领域知识学习的一致性路径:大概念统领整合学习
大概念是联系整合概念基础上再抽象提炼的概念,是“处于更高层次、居于中心地位和藏于更深层次,兼具认识论、方法论和价值论三重意义,因而更能广泛迁移的活性观念”[4]。我们可以通过深度解读教材,了解知识的前移后续、本质内涵,从中抽取出知识内核,形成大概念;也可以从《标准》中提出的核心素养——数感、量感、符号意识、空间观念、推理意识、数据意识等入手,从这些经过抽象概括出的核心素养中提取大概念。大概念强调数学思想和精神上的一致性,是对核心素养的统摄与整合。例如抽象能力和推理能力中都强调了从现实世界出发,从已知的数量关系和事实入手,逐步脱离具体事物而转向进行思维的操作,这样的过程其实是一种 “转化”。由“转化”这一大概念统领“数与代数”领域中有关“数的运算”(自然数、小数和分数的四则运算)和“图形与几何”领域中有关“图形的认识与测量”(多个平面图形的面积计算)的学习,跨领域的学习中都采用了转化的思想方法。具体来说,都是沿着未知转化为已知、将复杂转化为简单、将具象转化为抽象的路径展开学习,通过有效的转化路径,解决新的问题。而学生对转化过程中“变与不变”问题的辩证思考,就是将新旧知识进行对比、关联、抽象和类推的过程,从中发现知识内涵的一致性,发展抽象、推理等高阶思维。
2.领域内知识学习的一致性路径:问题串引领递进学习
大概念具有的广泛迁移性和适应性,可以推动学生站在更高的位置思考,但是对具体的某一领域的问题,针对性较弱。在某一领域内知识的学习,必须基于知识内在的紧密结构,寻求思考方法、策略的统整,帮助学生形成某一领域的系统策略结构。小学生的思维元认知能力还处在发展初期,难以发现承载于知识背后的学习方法和策略,所以教师可以使用问题串引领,帮助学生进行有步骤、分层级递进式学习。提出的系列问题除了适应领域内知识结构的学习,更重要的是关注思维的一般过程,使其具有在领域内的强迁移功能,并利于学生多层次、多角度体验和观察,促进程序性、反思性和批判性思维的发生。例如“图形与几何”领域中有关图形的认识,可以设计以下的问题串,引导学生开展学习(见表1)。
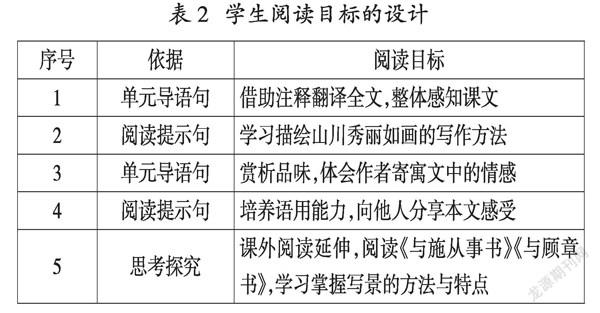
苏教版《数学》“综合与实践”中有一系列知识——“解决问题的策略”,八个策略贯穿三至六年级,这一系列内容可以进行较为统一的学习路径设计(见表2)。
3.单元内知识学习的一致性路径:结构化学材贯通化归学习
小学数学教材中的多个单元知识点,围绕一个具体的主题展开,结合不同年龄阶段儿童学习认知的特点,经常会把一个主题分多次、小单元进行学习,这就是所谓的“螺旋上升”式的教材编排方式。这样的小单元知识点较少,知识之间的关联性更强,前后衔接紧密,所以在学习中更要体现统整的思想,让这些知识点尽快“结网”,并促进学生进行思维的“内化、深化和缩减”[5],成为后续更高级心理思维操作的“对象”。在实际学习过程中,可以开发结构化学材包,贯穿单元学习的各个心理阶段。结构化学材是结构关联的学习材料,既关注知识结构的关联,也关注认知结构的关联。结构化学材是在单元整体甚至跨单元、跨学科视角下对教材内容进行重组,基于儿童认知特点,指向儿童结构性思维发展的可视化、易操作的工具支架,它采用形式多樣的表达形式,吸引儿童注意,适合儿童同时进行外在的具象操作和内在的心理经历,支持儿童思维向纵深发展。下面就以苏教版《数学》三年级下册“小数的初步认识”单元为例,描述结构化学材引领学生开展具体学习的轨迹:
“小数的初步认识”利用结构化的学材包,支持学生一致性的学习过程,有效地贯通知识点之间的联系,并将小数纳入到自然数体系中,形成了自然数和小数整体性的知识网络。
一致性视角是小学数学教师分析教材和设计学习过程的全新视角,可以帮助教师更好地理解学习,落实“学为中心”的思想,聚焦如何“减负增效”。而在一致性视角下进行的数学学习,也必将让学生学得有趣、学得轻松、学得深刻。
参考文献
[1] 殷娴,杨涛.小学数学课程“数学思考”目标体系的构建[J].课程·教材·教法,2017,37(03):82-89.
[2][3] 张良.深度教学 “深”在哪里——从知识结构走向知识运用[J].课程·教材·教法,2019,39(07):34-39+13.
[4] 李松林.以大概念为核心的整合性教学[J]. 课程·教材·教法,2020,40(10):56-61.
[5] 林崇德.试论思维的心理结构研究[J].北京师范大学学报,1986(01):18-26.
*该文为南京市“十四五”教师教育综合改革研究专项课题“知行合一:小学生数学实践智慧的培育研究”(LJG\2021\09)的研究成果

