基于随机事件的教学研究
焦 岑,孙唯唯,聂家升
(苏州大学 应用技术学院,江苏 苏州 215325)
概率统计是学生在中小学阶段就已经接触过的内容,其中的事件之间的关系与运算、古典概型、事件的独立性、二项分布、正态分布、数学期望、方差、列联表检验等知识学生在学习这门课之前已略知一二,这就使得学生在初始学习阶段,很容易对这门课的重要知识点掉以轻心,从而导致其在后续的其他知识点的学习中学习成绩一落千丈,学习效果一塌糊涂。
1 随机事件的概念
概率统计第一节的知识点是随机事件,随机事件的定义非常简单——样本空间的子集,而样本空间表示的是随机试验的所有可能结果,在概率统计里学生接触的大多数试验都属于随机试验,随机试验的条件是:(1)试验在相同的条件下可以重复进行,(2)试验的所有可能结果不止一个,且在试验前都能明确其所有可能结果,(3)试验开始前不知道会出现哪种结果。我们将满足以上三个条件的试验称为是随机试验。随机试验的定义非常简单,其试验的所有可能结果也非常容易找出来,故样本空间是学生可以明确的,而样本空间的子集——随机事件,学生很容易忽略其为集合的要求,随意地写出样本空间及随机事件。
例如:抛掷三枚硬币,正面向上记为H,反面向上记为T,写出试验的样本空间和事件A={恰有一枚正面向上}。像这样一道简单的问题,大部分学生的答案都是
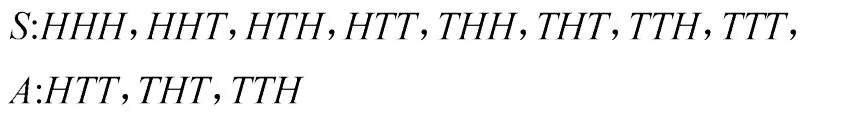
而正确的答案是
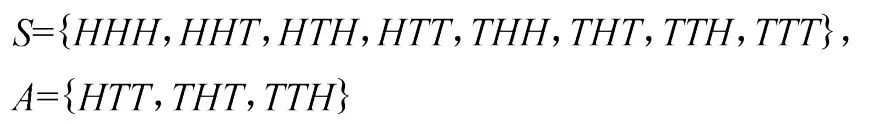
这虽然是不起眼的小细节,但也侧面反映出学生学习态度不端正,继而对后续知识点的学习效果大打折扣。故这就需要任课教师在该课程的教学伊始,了解到学生可能出现的问题,在授课的过程中,有的放矢地提醒以及严格要求学生注意该知识点,附加在布置的作业中有所体现,从而强化学生对该知识点的理解与掌握,规范他们的解题过程,端正他们的学习态度。
2 事件间的关系及运算
由于随机事件贯穿整个概率统计课程的第一章,所以对于随机事件的学习与讲解还有其他额外需要注意的地方。在讲完随机事件的定义后,知识点来到了事件间的关系及运算。该部分内容主要讲的是事件的包含关系、相等关系、互不相容关系、和事件、积事件、差事件、对立事件。
事件间的关系及运算是我们后续学习与计算随机事件的概率的一个重要方面,所以在学完了随机试验、样本空间与随机事件这三个知识点的定义后,随机事件与随机事件之间的关系及运算,在多个不同的随机事件之间如何寻求某一事件的发生就显得极为重要。
2.1 包含关系、相等关系
在这些事件的关系及运算当中,包含关系、相等关系是两个较为简单的关系,学生学起来并不复杂,记住关键词就可以了。积事件呢,由于表示的是所有事件同时发生的一个事件,所以学生理解起来亦不复杂,只需要注意积事件的符号即可,不要跟和事件的符号混淆。
2.2 和事件
和事件主要是学生无法理解“至少有一个事件发生”的含义,更别提“至少有多个事件发生”的含义了。大家都明白,“至少有一个事件发生”即是在若干个事件中,发生的事件个数大于等于1即为这个事件发生了,或者说,在若干个事件中,只要有一个事件发生了,那么这个事件就发生了,这个事件本身表示的是若干个事件中的一种“或”的关系。例如,A∪B表示的是要么A发生,要么B发生,要么A、B都发生,只要有其中一种情况出现,那么A∪B这个事件就发生了。所以和事件 A∪B表示的是并符号左右两端的事件至少发生一个,就可以认定为该事件发生了。理解好了和事件,对于后续做加法公式之类的题目,也会方便很多。
更加复杂的和事件是,每一个并符号两端又涉及多个积事件,例如等等,这又变相增加了学生学习的难度,以及教师若未做足功课前,教学过程中的困难。因此,和事件其实更准确的来说应该是若干个并符号的两端至少有一端的情况会出现,即至少有并符号左右所写出来的这些事件中的某一个事件会出现,而每一个写出来的事件也很有可能是多个事件的积事件。
2.3 差事件
差事件就是一个事件发生,另一个事件不发生,类似于学生小学阶段学过的减法,被减数减去减数,减数要从被减数中挖除。所以差事件也是,不发生的事件要从发生的事件中挖除。如事件A={1,2,3},B={2,3}则A B={1}。但差事件比较复杂的地方在于其又可以表示成发生的事件与不发生的事件其逆事件的积事件,即A-B=A,这从韦恩图中可以看出。
此外,差事件是一个事件减去另一个事件,但是前者事件和后者事件之间不一定是前大后小的,也可能前小后大。这亦跟减法运算一致,学生在刚开始学习减法运算时,被减数一定是大于等于减数的,但是在引入负数的概念后,学生会发现被减数可以小于减数,只不过结果是一个负数而已。但是集合与集合之间的相减则不会出现负集合了。集合与集合相减,一方面,从减号前面的集合里找出与减号后面集合中所相同的元素,然后两者相消;另一方面,从减号前面的集合里找出与减号后面集合中所不同的元素,保留减号前面的集合里的不同元素下来成为结果。
例如,在下面两个集合处于不同的关系中,集合与集合之差的结果是不同的:
由此可见:无论前者集合有多小,后者集合有多大,也不会出现负的情况,这是一点。其次要注意的是,差事件减去的究竟是什么呢?我们从前面的例子中发现,当两个集合之间有相同元素,最后相同元素会从结果中消失;若没有相同元素,则保留减号前面的集合中的所有元素。所以,一个事件减去另一个事件本质上是这个事件减去了另一个事件与自身的积事件,因为积事件中包含的就是这两个事件中的相同元素,即A-B=B-A。这对于后续求解差事件的概率是非常重要的一个知识点,学生务必得先理解概念,否则后续的学习也将问题百出。
2.4 对立事件和互不相容关系
对立事件和互不相容关系是比较容易混淆的两个知识点,对立事件也称两个事件互为逆事件,简称互逆;互不相容事件也称互斥事件。在这样的别名也有点相似的地方,学生更容易混淆两个概念。因此,教师如何帮助学生梳理这两个知识点的异同就显得格外重要。我们先简单来看一下这两个知识点的定义,了解了定义之后,再有的放矢地想办法帮学生区分、辨别这两个知识点。因为在本人若干年讲授概率统计课程的过程中,越来越意识到从定义出发的重要性,概率统计中基本所有的知识点都可以从定义本身去理解,去做题。定义是知识点的初衷,所以学生如若能做到将所有知识点的定义都掌握,后续的学习,也不会有太大的困难了。
那么,对立事件的数学化定义是什么呢?不妨记互为逆事件的这两个事件为A、B。对立事件的定义是事件A、B在每一次试验中有且仅有一个发生。这个定义可以拆分为两方面的含义。一方面,事件A、B在每一次试验中得有一个事件发生,要么是A,要么是B,不能再出现第三个事件,所以A与B构成了整个样本空间,用数学语言写出来即是A∪B=S。另一方面,事件A、B在每一次试验中只能有一个事件发生,就是说,如果A发生了,那么B一定不发生;而如果B发生了,那么A也一定不发生,而这样的两个A、B是什么状态呢?就是A、B不能同时发生,而A、B不能同时发生,也就是事件的互不相容关系。因为两个事件不能同时发生,则称这两个事件互不相容,这就是互不相容的定义。不妨记两个互不相容的事件也是A和B,因为A和B不能同时发生,故使得A和B同时发生的元素不存在,用数学语言表示出来就是A∩B=。至此,对立事件的数学化定义则出现了:且A∩B=。而事件互不相容的数学化定义仅有一个A∩B=。故经常放入考试中的一道题是,互不相容和互逆,两者的关系是,充分必要?充分不必要?必要不充分?还是既不充分也不必要呢?所以学生需要从定义法去理解知识点,教师也最好从定义法去讲授知识点,毕竟,某知识点的定义才是该知识点一切后续定理或者考点的开始。
其次,如何帮助学生更好地分辨这两个概念本身呢?因为如果学生从看到文字后便对这两个知识点产生了混淆,那么即使是记准了每一个知识点具体的定义,最终的结果仍然是南辕北辙。关于该问题,本人一些的想法是,可以从文字本身出发,毕竟题设也是文字。那么对立、互逆、互不相容、互斥,如何辨别呢?首先,对立相对而言可能是比较容易的,因为对立就表示两者站在对立面,两者站在对立面的话,就是非你即我、非我即你的状态了,有点类似于比赛中的1V1。同样,互不相容是另一个相对比较容易理解的概念,因为互不相容就是两者不能共存,互相不能容纳下对方,也就意味着两者不会同时发生。但该概念又与对立不同,只表示两者之间互不相容,不代表没有第三方的出现。有点类似于比赛中的1VN。互逆和互斥是学生最容易混淆的地方了,因为这两个词语之间,共用了一个“互”字,仅在于互后面的那个字不同。而“逆”字,意为取其否,即为相反面,且“逆”字本身也有相反的释义,故可以理解为对立的意思。所以,两个事件互逆本身就是这两个事件是对立事件的含义。另一方面呢,互斥中的斥,我们给它组词,就是排斥,互相排斥,而排斥本身并没有任何对立面的含义在其中,只是说排斥对方,因而不会和对方同时发生,至于会不会和其他的事件同时发生就不得而知了,至少字面意思无法窥探到。中华文化博大精深,在数学中的体现亦如是。较为容易混淆的两个数学术语,使用语文中的组词一法,两者的区别或差异,高下立现。所以,学生在学好数学的同时,也不能丢弃汉语言文学的学习,毕竟知识点都是相互贯通的。活到老学到老,果真如是!
3 随机事件的表达
随机事件的表达也是随机事件这个概念本身最复杂的一个知识点,准确无误地表达随机事件,对于后续求解随机事件的概率可以做到事半功倍的效果;而错误地表达随机事件,不仅可能造成概率计算的偏差,也可能导致解题过程中错失很多得分点。毕竟,有了随机事件,我们才可以去计算随机事件的概率,这是很多学生意识不到的地方,任课教师需要不断点播,尤其是到了全概率公式和贝叶斯公式部分,很多学生知道概率如何计算,可由于没有写出随机事件,没有表示出每一个事件,导致其计算结果即使对了,也得不到几分,因为没有体现全概率公式和贝叶斯公式,没有体现概率的精髓,只是将无意义的数字做加减乘除,这完全不能称上是概率论的学习。故随机事件的概念跟后面其他的概念相比虽然是一个比较小的知识点,教材将其放在第一节,也是因为该知识点非常简单,但是如果任课教师在课前没有做好充足的准备,没有对可能出现的情况进行一定的预判,那对于学生后续的学习来说,或者对于教师后续的授课来说,都极为痛苦,也极为困难。
关于随机事件的表达,一方面是为了后续计算概率的方便,可以自由地使用加法公式、减法公式、乘法公式、全概率公式和贝叶斯公式等;另一方面也是课程本身的需要。既然学生已经学过了事件间的关系及运算了,那么多个事件的表示,若干个事件的发生情况都属于该知识点的一个后续,自然也会随之而来。
诚如上面所说,学生不仅要学会如何用数学语言表示事件,还要学会理解被表示出来的事件的含义。而显然是,理解被表示出的事件于学生而言更加容易,而这方面的例题,在很多的教材中却不曾体现。所以,任课教师在授课的过程中可以穿插理解事件含义的例题,如 A={甲来上课},B={乙来上课},则AB={甲、乙至少有一人来上课},∪={甲、乙至少有一人来上课}等等。这样学生在之后去主动地表示事件时,更易发现自己用数学语言表示的事件是否与事件本身的含义相同。
如此下来,第一节随机事件的概念就差不多完全讲透了。但课后习题的布置也不能马虎,这也是考验学生是否学明白的一个标准。任课教师可将随机事件的表示这部分知识点的课业布置得稍多一点,一方面旁敲侧击地让学生意识到该知识点的重要性;另一方面可以让学生花费更长的时间去理解该知识点,消化该知识点。
随机事件这一知识点看似简单,实则复杂,因为该知识点不仅只涉及其本身,还会引申出后续其他知识点的学习,如若学得不够透彻,后续的学习情况则会更加糟糕。希望各位老师多多加以重视,也希望各位同学多多加以关注。将概率统计课程学好,后续其他课程的学习也一定会增光溢彩。

