储能双向响应系统中双向变流器闭环稳定性建模

李 波，杨永标

(1.广东电网有限责任公司 电力调度控制中心，广东 广州 510600； 2.东南大学，江苏 南京 210000)

1 引 言

储能被认为是解决大规模能源发电的有效技术，储能双向响应系统可以为发电系统与电网之间提供过渡电气接口，提高并网发电质量，保持运行稳定[1]。它可以根据用电高峰及用电低峰的不同情况，输送及储存电能，因此该系统具有削峰填谷作用。其中变流器虽然结构简单，方便控制，但是会造成电网谐波污染，特别在深度调节情况下，系统功率较低，使谐波污染尤为严重，影响储能效果。

为改善上述现象，相关学者提出如下建议。张辉等提出三电平NPC变流器闭环控制方法。这种方法对比双调制波载波调制直流电压利用率、电器开关损耗、谐波电流畸变率，获取载波调制策略，抑制非调制因素引起的电压失衡[2]。辛征等人设计了MES装置用电压源型变流器双闭环功率控制系统。该方法利用超导磁储能装置，设置双闭环功率控制系统中参数，建立电压源转换器数学模型，推导参数计算公式，获得控制器各参数变化特性及影响规律[3]。

上述两种方法一定程度上抑制了系统谐波污染，达到功率平衡与灵活运行效果，但缺乏严格完整的闭环系统稳定性研究，导致储能系统稳定性较差。基于此，本文构建双向变流器闭环稳定性模型。变流器属于储能系统控制环节，可实现交流侧和直流侧的能量双向流动，根据对其系统结构设计，综合考虑谐波分量影响，分别构建电压外环和电流内环控制模型[3]，实现闭环稳定性建模。

2 双向变流器系统结构设计

2.1 变流器工作模式分析

本文研究的变流器属于自带LCL型滤波器的PWM(pulse width modulation)拓扑结构[4]。假设ua1、ub1与uc1分别为三相电网电压，V；ia1、ib1与ic1代表侧电感电流，A;iCa、iCb、iCc是经过电容的三相电流，A；M1与M2分别描述网侧电感与桥臂侧电感，H；R1和R2分别表示网侧电感与桥臂侧电感的寄生电阻，Ω。

为使变流器系统结构更加简便，通常忽略滤波器中阻尼电阻与滤波电容，并将其当做M型滤波器，因为在低频处这两种滤波器的频率特征相同，通过相电压与相电流之间的联系，根据基尔霍夫定理[5]可以获得：

U1=RI+jωMI+U2

(1)

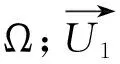
为使本文所设计的双向变流器具备电能双向传输性能，需要确保变流器在四象限中运行。在整流充电过程中变流器为PWM整流工作模式，而在并网放电时为逆变模式。

2.2 双向变流器电路设计

现阶段变流器充电方式较多，充电方法是否科学合理直接影响储能电池的使用寿命。以下为几种常见充电方式。

(1)恒定充电：在充放电的时，电流是不变的。这种情况下，电池的电压会逐渐升高，而电流会变大，充放电的持续时间也会变短。如果要提高充电速度，此种方式较为理想，但是在充电完成后电流依旧维持不变，因此降低电池使用寿命，所以在实际应用过程中，这种方式一般不会单独使用。

(2)恒压充电：充电过程中电压不变，电流逐渐减少。充电初始电流较大，高于允许最大电流值。在充放电过程中，电流不断减少，能够避免大电流导致的活性物质脱落与电能损耗。此种方式缺陷在于当电流很大时，电极活性物质体积变化非常快，降低机械强度，且在充电末期电流过小，极板深层活性物质不能得到较多充电反应，出现长期充电不足等情况，对电池伤害较大。

(3)恒压浮充[6]：针对使用频率较低的电池，为改善电池自放电带来的能量损失，必须对其进行长时间低电压充电，即恒压浮充。这种充电方式能够减少电池析气率，还能防止电流过大，使充电设备始终保持稳定工作状态。当电源供电不足时，电池能输出强大电流，确保电源设备电压恒定。但是恒压浮充会导致个别电池充电不均匀。

本文根据上述充电方法优缺点，利用三种方法相结合的智能充电方式[7]。初期采用恒流充电，之后转换为恒压充电，最后使用恒压浮充。此种设计方法改善了恒压充电初期电流过大和充电结束时电流过小导致的活性物质不能获得充电反应的缺陷，以进一步改善恒流充电后期电流过大造成的活性物质脱落现象。

本文充电方式不但可以实现能量双向流动，还可以观测到电压值的实时变化。假设三相电网电压为对称形式，主开关为理想开关，不考虑电感的饱和因素，则单极性二值逻辑开关函数sk定义如下：

(2)

因此得出三相静止坐标系中变流器数学模型：

(3)

式中：iL为直流侧负载电流，A;ia、ib与ic均为网侧相电流,A。

根据三相对称原理可以得出：

(4)

假设在abc三相静止坐标系中，对变流器分析时必须对三个变量分别进行分析，此时变量数目较多会给研究工作造成不便。为改善这一问题，将abc三相坐标系下的变量，通过Clark转换到αβ两相静止坐标系中。坐标系变换矩阵为

(5)

两个坐标系的反变换矩阵为

(6)

结合式(6)所示的变换关系，对式(3)进行坐标转换获取双向变流器在αβ两相静止坐标系中的数学模型：

(7)

式中：Ua1、Uβ1分别为三相电压在aβ轴上的分量，V;ia2与iβ2为变流器侧电流在aβ轴上的分量,A。

结合等幅变换理论[8]，aβ两相静止坐标系变换到dq旋转坐标系的矩阵表示为

(8)

利用上述变换关系，可以得出双向变流器电路数学模型：

(9)

式中：id2、iq2为变流器侧电流在dq轴上的分量，A;sd与sq为开关函数在dq轴上分量。至此，完成变流器电路的设计，为变流器闭环稳定性建模基础做准备。

3 储能响应系统双向变流器闭环稳定性控制

典型的电压外环闭环控制模型如图1所示。Gi(t)是Ip(s)到US(s)的传递函数，Gi(t)是PWM发生器的传递函数，Hv(s)是分压器网络的传递函数，Gpi(s)是误差信号US(s)到Vp(s)的传递函数。

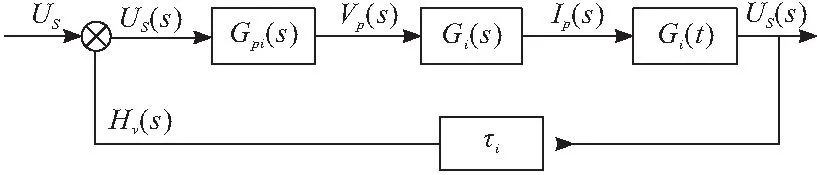
图1 电压外环控制模型

系统G(s)H(s)的开环传递函数由以下四部分组成。

G(s)H(s)=τiGi(s)Gi(t)

(10)

在设计闭环补偿控制模型时，最终电路的开环传递函数应满足稳定性判据：

(1)在开环传递函数的交叉频率下，系统应具有至少35°～45°的相位裕度。

(2)为了防止电路相位的快速变化-2斜率，系统的总开环增益和交叉频率的斜率应为-1。

(3)增大带宽能使系统的响应速率和动态性能得到明显的改善。随着频率的增加，系统的动力学性能得到改善。但是，按照采样原理，交叉频率不能超过开关频率的二分之一。由于采用了高频分量可以有效地消除由寄生振荡造成的干扰，所以通常将交叉频率设定在1/5～1/20。

原回路开环传递函数为

(11)

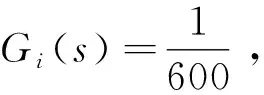
图2 原电路开环传递函数Bode图

为了改善原系统的频域特性，需要加入闭环补偿控制模型。采用 PID控制方式，在原有的系统中加入了新的极、零点，以提高原有的系统频域性能，使其具有较好的稳态及动态学性能。为了增加高频衰减斜率，有效抑制高频噪声，在PID控制中加入一阶振荡环节，提高系统的高频抑制能力。因此闭环补偿控制系统的传递函数如式(12)所示。

(12)

修正后系统的开环传递函数如式(13)所示。

(13)

从Bode图3中可以看出。开环系统的交叉频率为62 900 rad/s，即10 015 Hz，相位裕度为55.2 °。从而验证了系统的稳定性判据，表明闭环补偿控制系统的传递函数满足设计要求。

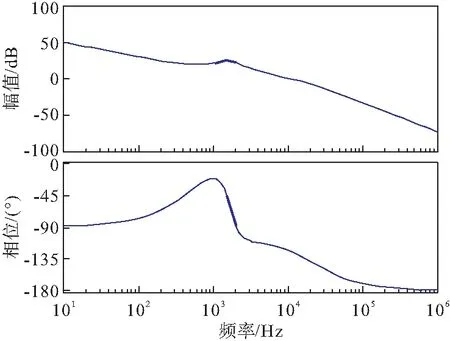
图3 修正后开环传递函数的Bode图

通过PID控制增加新的极点和零点，使系统满足上述稳定性准则。同样，校正后的系统开环传递函数为式(14)。

(14)

Bode图如图4所示。

图4 修正后升压模式开环传递函数Bode图

从图4可以看出，系统的交叉频率最终为4 kHz，相位裕度为52°，在正零点频率处，相位迅速减小，高频时相位滞后增大。结果表明，系统最终满足稳定性要求。

4 仿真实验数据分析与研究

为验证双向变流器是否具有稳定性能进行仿真实验。实验参数如表1所示。

表1 实验参数表

图5为利用本文方法获取的双向变流器闭环系统零极图，从图5中可以看出，所有产生的零极点均在单位圆内。因此，该建模方法确保了储能双向系统的稳定。

图5 电流内闭环系统零极图

为进一步证明本文建立闭环稳定性模型的有效性，对比文献[2]方法和文献[3]方法分别在正常情况下与突加负载情况下对储能双向响应系统输出的电压波形，结果如图6、图7所示。

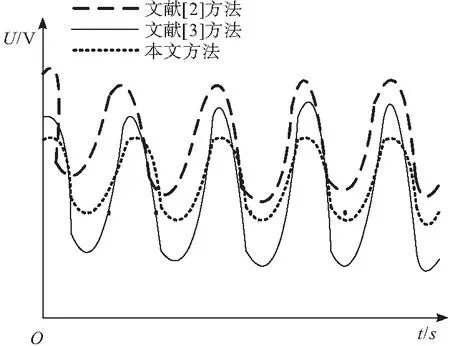
图6 双向响应系统输出电压波形对比图

图7 突加负载情况下输出电压波形对比图

从图6、图7中可以看出，在系统正常运行时，不同方法输出的电压波形起伏情况相差较小，相对稳定。但是在突加负载状况下，文献[2]、文献[3]方法输出的电压波形畸变严重，而本文方法依旧可以输出较为平稳的波形。这是因为所提方法加入了电容，减少对谐波干扰，使系统输出波形更加平稳。

5 结 语

为提高储能系统稳定程度，本文分别构建电压外环与电流内环控制模型，实现双向变流器稳定性建模。仿真实验证明，该方法获取的零极点均在单位圆内且输出电压波形平稳，能够满足储能系统稳定运行的要求。然而构建电池功率模块成本较高，在今后研究中需要综合分析大功率转换器和智能电路功能复合的可能性，对原有电路进行简化。