基于改进AHP法和改进熵权法结合的组合电量预测模型
张杰,薛太林,解张超,闫祥东
(山西大学 电力与建筑学院,山西 太原 030013)
0 引 言
精确的电量预测是电网安全经济运行的前提,也对国民经济起着至关重要的作用[1]。
传统的单一预测方法如灰色模型[2]、神经网络[3]和回归分析[4]等预测方法各有其特点,但难以全面表现历史电量的变化规律。针对上述问题,文献[5]提出了基于奇异谱分析与神经网络的中期负荷分解预测模型,文献[6]对随机森林预测方法进行改进使其与经济因素相结合,文献[7]提出一种STL模型并将其与时间序列结合进行电量预测。
本文采用多种预测方法结合的组合预测模型来避免单一预测方法的局限性。对于组合预测模型,如何对各模型进行权重分配是问题的关键。本文将改进层次分析法(AHP法)和改进熵权法相结合形成组合权重计算方法,计算各单项预测模型权重得到组合电量预测模型。最后以某地区一个月为例,对其进行电量预测并与实际情况相比较,结果表明,使用基于改进方法的组合预测模型可有效提高预测的精确性,降低预测误差。
1 改进的AHP法原理
1.1 构造判断矩阵
将各个准则两两比较重要性并进行量化,按1-9标度法(表1)构造判断矩阵Z为:
Z=[zij]n×n
(1)
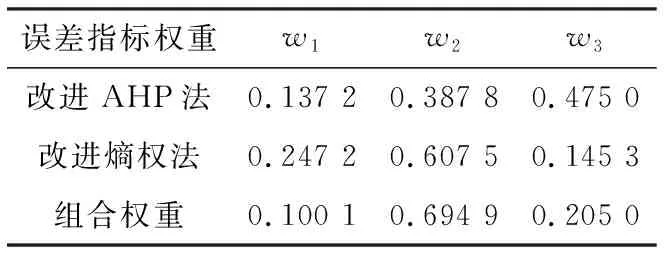
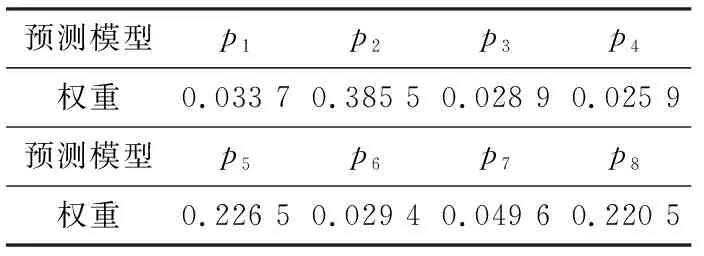
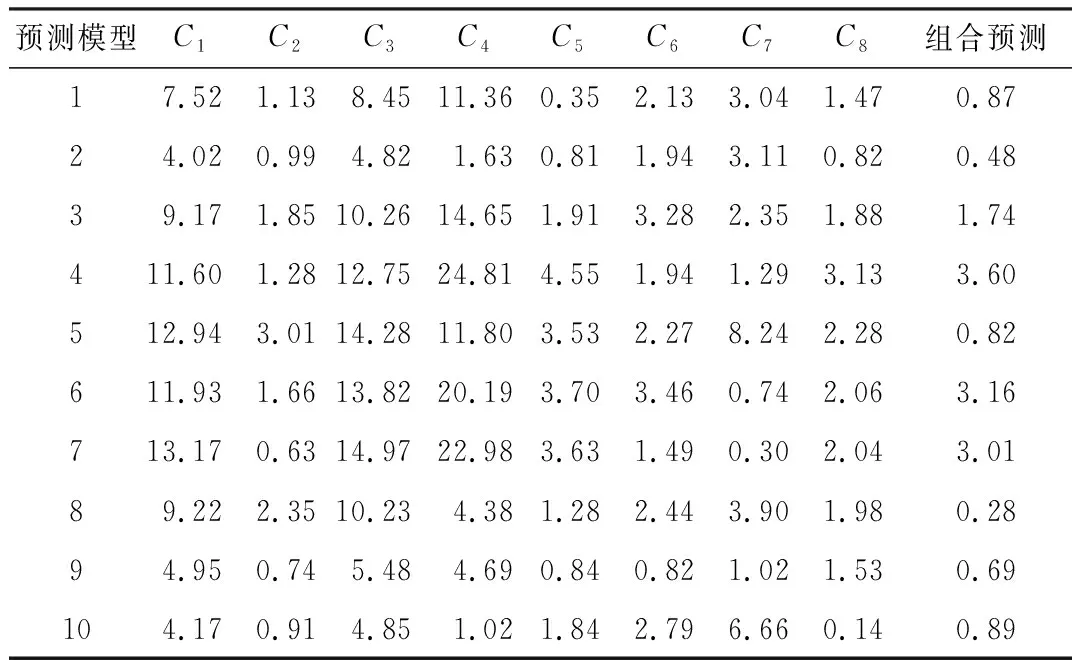
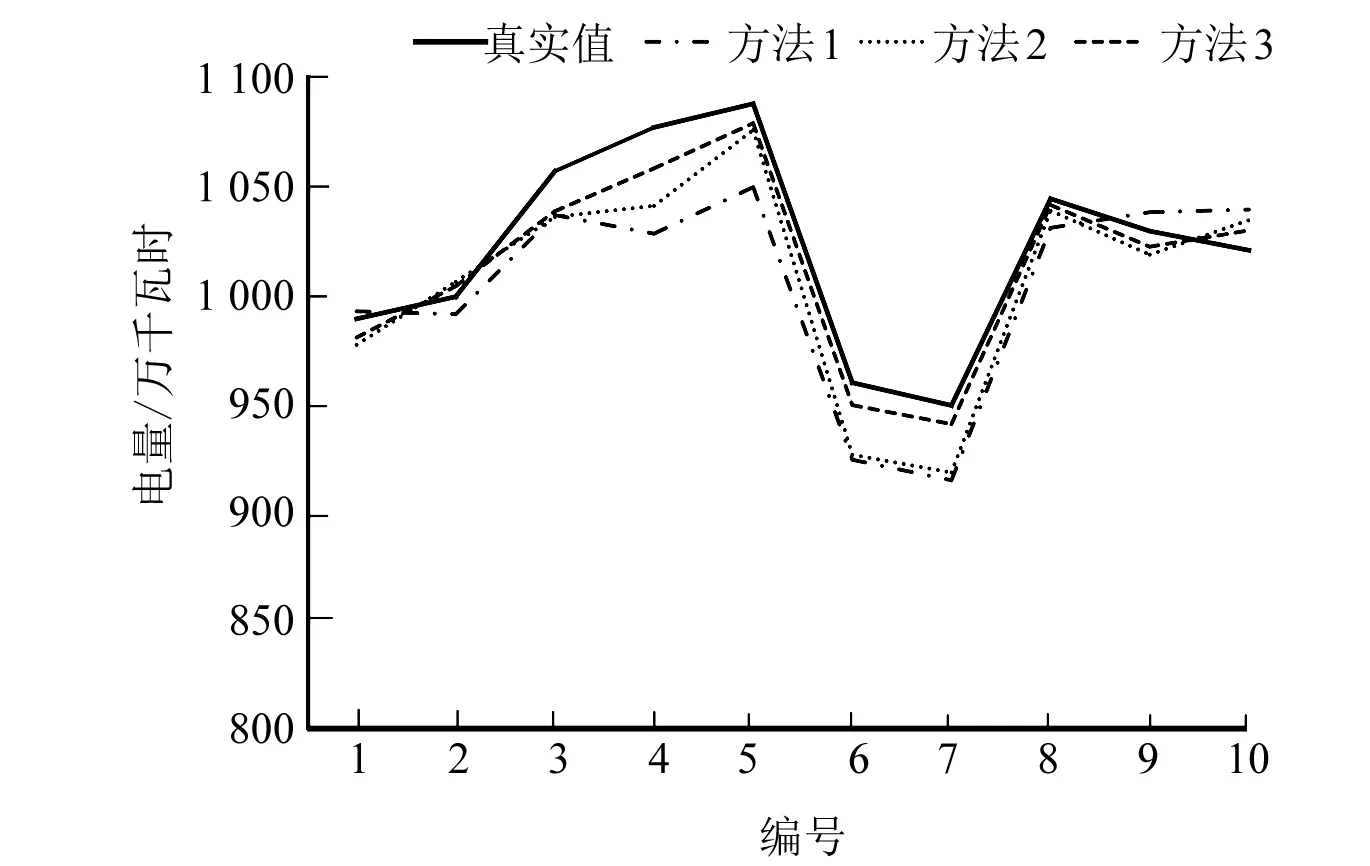
式中:n为指标的数量;zij为矩阵元素,表示准则i相对准则j的重要性。在传统层次分析法(AHP法)中,量化标准为1-9标度法,如表1所示。在改进方法中,对z11,…,z1n和z21,…,zn1,仍然沿用表1的标度法;对任意1 表1 1-9标度法 (2) 上述方法构造的判断矩阵Z满足一致性的定义:对任意i,j,k=1,2,…,n,zik=zij×zjk。因此,判断矩阵Z具有完全一致性,无需进行传统AHP法中的一致性校验和调整。 计算判断矩阵Z最大特征根的特征向量α: (1) 将Z的每一行求乘积,得到向量O: (3) (2) 对向量的各元素进行n次方根计算,得到向量θ: θT=θ1,θ2,…,θn= (4) (3) 对向量θ进行归一化处理,得到向量α,即得到了分配权重: (5) 假设给定了k个指标,n个模型。那么有: (6) 式中:Xi为第i个指标下所有模型的数值,共有n个,Xi={x1,x2,...,xn};Xij为第j个模型下第i个指标的数值;Yij为第j个模型下第i个指标数值标准化后的值,j=1,2,…,n,i=1,2,…,k。此时信息熵为: (7) 通过上式计算信息熵为E1、E2、…、Ek,通过信息熵计算各指标的权重: (8) 式中:γi为第i个指标的权重。此处对熵权法进行改进,以修正在多熵值分布趋于1的情况下,权重分配会出现混乱的缺陷,其改进公式为: (9) (10) 本文采用以下三种误差指标: (1) 纳什系数X1 (11) (2) 平方误差X2 (12) (3) 均方根误差X3 (13) 本文用到的算法库如表2所示,共有八种预测算法。 表2 预测算法库 (14) 式中:yi为一种模型在第i个指标的评价值。由此可得第j(j=1,…,n)种预测模型在第i(i=1,…,k)种误差指标下的误差评价值yji, 误差评价矩阵Y为: (15) (16) 得到其重要性熵值计算式: (17) 式中:Ei为第i个指标下的熵值。将Ei代入式(8)~式(10)得出改进熵权法下误差指标的权重βi。当与改进AHP法相结合时,组合权重为: (18) 式中:wi为两种方法组合时的权重;αi为改进AHP法下的误差指标权重。 (19) 算法流程图如图1所示。 图1 算法流程 某地区过去几年某月的用电量如表3所示(数据已做脱敏处理,以三天为一组,共十组),预测该地区2019年的电量并与实际电量对比。 表3 某地区用电量 单位:kWh (1) 将纳什系数重要性的量化标度相对于自身确定为1,相对于平方误差确定为2,相对于均方根误差确定为3。则有判断矩阵Z: (20) (2) 对2013年至2018年的数据利用八种预测模型分别进行预测,并用多误差指标体系进行评价,结合某组电量在该月用电量的占比进行加权,得到该月相对误差以及评价矩阵Y: (21) 应用改进AHP法和改进熵权法分别计算各误差指标的指标权重,并将其结合得到误差指标的组合权重,结果如表4所示。 表4 误差指标权重分配 (3) 确定组合算法权重。根据式(19)计算八种预测算法的权重pj(j=1,…,8),其中各预测模型的参数设置均通过对比分析采用最佳参数值,且计算结果均为执行多次进行预测得到的平均值,结果如表5所示。 表5 各模型权重分配 基于电量原始数据,比较八种单项算法和优化组合模型2019年某月电量预测结果的相对误差。对比结果如表6所示。 表6 八种预测算法和组合预测的效果比较 单位:% 由表6可以看出,不同预测算法的预测误差有较大差异,其中算法C3和C4误差较大,而算法C2和C5误差较小,其他算法介于中间。而优化组合预测模型能够根据单项算法的预测效果,将改进的AHP法和改进的熵权法结合,改善各单项模型在组合算法中的权重,突出算法库中预测效果良好的模型,并提高其权重占比,从而得到更精确的预测结果。 (4) 不同算法预测结果对比。为了体现本文算法在预测算法优化中的可行性,本文同时引入其他两种预测方法进行结果对比,结果见图2。 方法1:利用单一预测算法预测(选取预测效果最好的算法C5)。 方法2:利用传统AHP法和熵权法结合预测。 方法3:利用改进AHP法和改进熵权法结合预测。 图2 不同算法预测电量 由图2可以直观地看出,相对于单一的预测模型和传统的AHP法和熵权法,方法3更加接近真实值,精确度更高,误差更小。 本文将多种预测模型结合来预测电量。在对各模型进行权重分配时,针对传统AHP法需一致性校验和调整,以及熵权法多熵值分布都趋于1时熵权分配紊乱问题。本文提出改进的AHP法和改进的熵权法来进行权重分配。经过算例分析证明了上述方法的可行性。结果表明,基于改进AHP法和改进熵权法的预测模型可以赋予预测对象误差指标以及组合算法中单项模型更合理的权重,形成基于预测对象特性的优化组合模型,从而改善预测结果。
1.2 计算分配权重
2 改进的熵权法原理
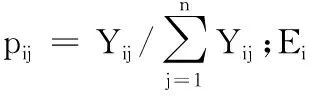
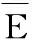
3 多误差评价体系及算法库
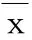

4 权重分配
4.1 误差指标的权重分配

4.2 各预测模型的权重分配
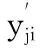
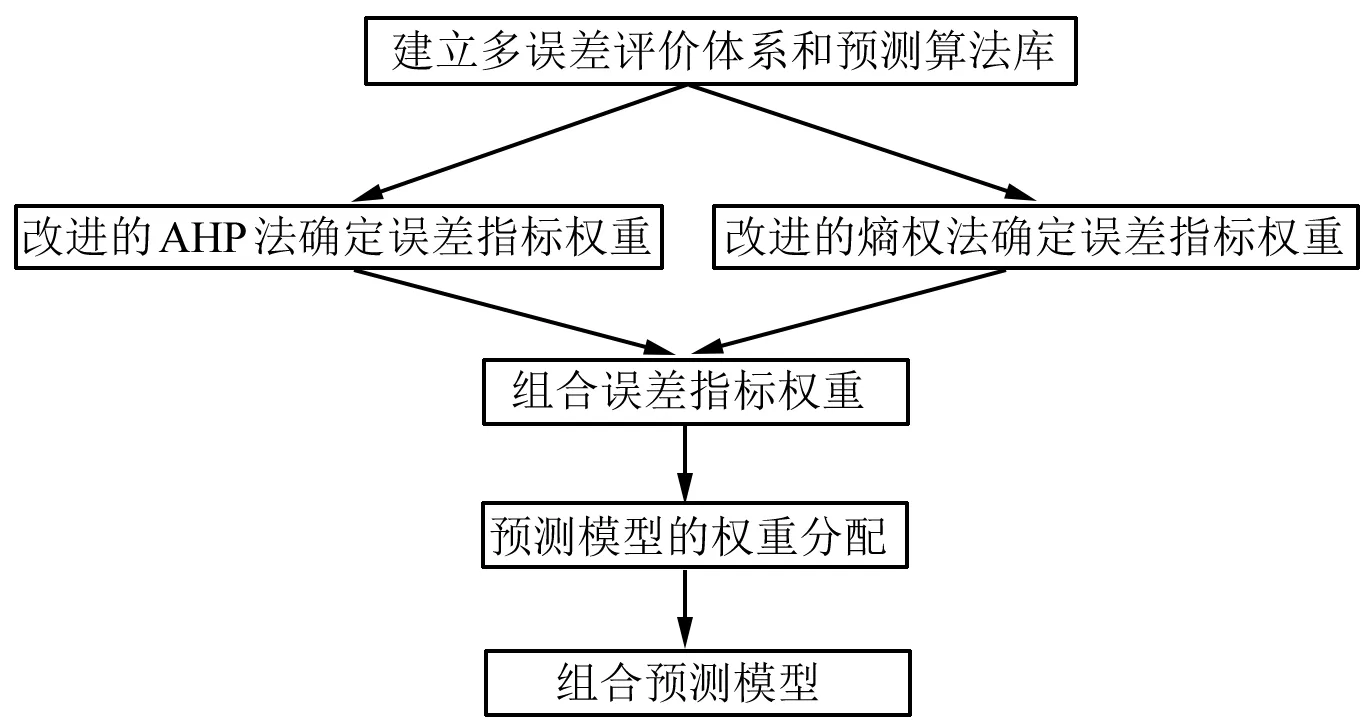
5 算例分析


6 结束语

