直流馈入的高比例新能源受端电网静态电压稳定分析
赵 伟, 黄子洋, 潘 艳, 徐 鹏, 李付强, 李庚银
(1.国家电网有限公司华北分部, 北京 100053;2.新能源电力系统国家重点实验室(华北电力大学), 北京 102206)
0 引 言
近年来,我国加快建设百万伏级交直流系统特高压电网为核心的坚强电力网架,高压直流输电(High Voltage Direct Current,HVDC)技术在“西电东送、南北互供、全国联网”的布局中得到广泛应用[1],青海—河南、准东—皖南、昆柳龙等特高压直流线路将会陆续建成并投运;同时,可再生能源呈现高比例并网的发展趋势,截至2020年底,我国可再生能源总装机容量达到9.3亿千瓦,占总装机规模的42.4%,开发利用规模稳居世界第一[2]。然而,随着大容量HVDC线路的馈入与新能源的高比例并网,受端电网呈现低惯量、低阻尼的特征,稳定性也受到了极大的挑战[3,4],其中电压稳定问题尤为显著。评估直流馈入的高比例新能源受端电网的电压稳定性对于电网的安全稳定运行尤为重要。
目前,有关学者已针对直流馈入后受端电网的电压稳定问题进行了大量深入研究。一方面,直流换流站会消耗大量的无功功率,长期无功缺额容易引起受端电网电压失稳与电压崩溃[5];另一方面,大容量直流的馈入削弱了交流受端电网的相对强度,进而影响了电压稳定[6]。通常使用短路比及其衍生指标分析并评估直流馈入后受端电网的维持电压稳定的能力。文献[7]考虑不同直流的控制方式提出了适用于直流多馈入系统电压支撑能力分析的临界和边界广义短路比,文献[8]提出了等效运行短路比以逼近运行临界值,更准确地评估了多直流馈入系统的临界电压稳定。然而,此类指标的有效性仅能通过时域仿真验证,且临界取值多依据经验,存在与电压稳定之间物理关联不明确的问题。
新能源渗透率对受端电网电压稳定的影响也逐渐成为电网运行关注的焦点,目前主要有两种研究思路,一方面,通过节点电压方程或者自建指标分析满足静态电压稳定的渗透率约束条件[9,10];另一方面,通过时域仿真分析大扰动后的暂态电压稳定性[4][11]。文献[4]通过仿真分析,得出随着新能源渗透率的提高,因其无功支撑能力较弱,系统失稳模式由同步机主导的功角失稳变为风电主导的电压失稳。文献[9]在其基础上推导了高比例新能源替代常规电源后系统静态电压稳定的临界指标,分析了运行点处节点无功对自身电压的灵敏度。文献[10]以静态电压稳定裕度为约束,研究了大规模新能源并网的临界渗透率,但并未论证电压稳定裕度在多场景下的适应性。文献[11]利用时域仿真法研究了分布式电源渗透率、容量等因素对受端暂态电压稳定的影响。综合来讲,虽可用新能源临界渗透率表征受端电压稳定极限,但尚缺乏对其更严密的理论推导支撑。
相对于暂态电压稳定分析,静态电压稳定分析具有更明确分析手段,但结论一般偏保守。受控制器影响,系统可能在达到静态临界点前发生其他形式的失稳,根据拓扑合理地选择评估指标直接决定了静态稳定分析的结论有效性。文献[12]采用电压稳定指数(Voltage Stability Index,VSI)分析了风电渗透率对电力系统静态电压稳定性的影响,当VSI≥0时表示系统电压稳定,反之则失稳。文献[13]分析并比较了λ特征值指标、dV/dQ灵敏度指标和L指标3种静态电压稳定性指标对于新能源接入点和渗透率的敏感程度,得出L指标的敏感程度最高,且在临界点处变化更快。文献[14]建立了基于L指标的静态电压稳定性区间评估模型,准确评估了可再生能源和负荷功率的不确定性对电力系统静态电压稳定性的影响;文献[15]基于局部电压稳定性L指标研究了风电场静态电压稳定性。
综上,国内外学者已在静态电压稳定分析指标上有深入研究,但鲜有在受端静态电压稳定分析中同时兼顾直流馈入与新能源并网的影响。为此,构建了包含直流逆变站、新能源的网络代数方程,考虑逆变器的运行特性与新能源的出力特性,将传统的用于判定交流系统电压稳定性的L指标推广到有直流馈入的高比例新能源受端电网中,并进一步推导了静态电压稳定临界情况下的新能源极限渗透率。本文深入地研究了高比例新能源对于有直流馈入的受端电网静态电压稳定性的影响,所得结论对未来电网规划具有现实的借鉴意义。
1 直流馈入的高比例新能源受端电网数学模型
1.1 受端电网基本结构
电力系统的运行特性可以由微分代数方程组描述,其中微分方程是描述元件时变特性的动态方程,代数方程是描述元件相互作用和网络拓扑约束的静态方程。进行静态电压稳定分析时不考虑元件动态过程,其主要目的是推导解析形式的电压稳定极限,首要步骤是构造代数方程来对网络进行合理数学描述。
直流馈入的高比例新能源受端电网的基本结构如图1所示。
为了简化分析,在建立网络代数方程的过程中将直流逆变站(本文所研究的馈入直流是实际系统中常见的LCC型直流)、新能源、常规火电机组以及负荷等元件用单端口进行等效。图中节点间由高电压等级输电线路连接。
设受端电网额定电压为UN(后文全部变量采用有名值计算),各节点视为该类节点集合的等效节点,可对接入各节点的元件进一步等效。
1.2 常规火电机组和直流逆变站节点等效
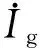
(1)
考虑到正常运行情况下Ug、Eg与UN相差不大,对式(1)进行了近似。
h为直流逆变站换流变网侧节点,母线电压表示为Uh∠θh。从LCC-HVDC运行特性入手对直流逆变站进行等效,已知逆变器准静态方程[16]:
(2)

从δ1<0可以看出,若不考虑无功补偿,直流逆变站在正常运行时可被视为无功电源,向受端电网发出无功,根据式(2)进一步得:
(3)
将节点h相角θh对应的旋转因子ejθh同时乘到式(3)左右两边,可得:

采用12脉动(n=2),并且为简化分析认为v=1,k=1,则δ1=-β,满足:
(4)
式(4)说明无论换流器的控制系统多么复杂,逆变站都可以由有阻抗的交流电压源的静态等效电路表示,该等效方法大大简化了后续的分析难度。图2展现了直流逆变站的拓扑模型与等效电路。

图2 直流逆变站的等效过程Fig. 2 Equivalent process of DC inverter station
1.3 新能源公共连接点和负荷节点等效
r为新能源并网的公共连接点(Point of Common Coupling,PCC),母线电压表示为Ur∠θr。考虑到风光新能源均采用最大功率点跟踪控制策略并网,只要Ur不严重偏离额定值,新能源出力仅取决于一次能源的特性(如风速、光照强度、温度等),基本不受PCC运行参数波动的影响,因此并网新能源可用恒导纳来进行等效[17],表示为
(5)
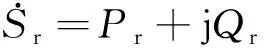
新能源的渗透率一般采用以下两种定义:
(1)对于集中式并网新能源,如送端风电采用风火打捆的形式送出,渗透率定义为风电容量与总发电量的比值;
(2)对于分布式并网新能源,如受端光伏分布式并入配网、含多新能源的微网,渗透率定义为分布式电源容量与配电网额定容量比值[18,19]。
本文采用第二种定义,设新能源和负荷有功功率分别为Pr、Pl,渗透率为ρ,则Pr=ρPl。
为了使新能源运行更加稳定,并网VSC逆变器留有最大的功率裕度以在紧急运行时为电力系统提供功率支撑,正常运行时无功控制指令一般设置为零,因此在后续的分析认为Qr=0。
l为负荷节点,母线电压表示为Ul∠θl。类似新能源,负荷节点为PQ节点,可用恒导纳来等效。
(6)

1.4 网络代数方程的建立和简化
以上对受端电网接入的各元件进行了合理等效,节点g、h可等效为带阻抗的交流电压源。节点r、l可等效为恒导纳接地。因此结合图1,可列写受端电网节点电压方程,即为静态电压稳定分析需要的网络代数方程。
(7)
式中:yh=1/zh。
进一步做出以下假设以简化后续计算分析:
(1)式(7)中互导纳Yij仅计及输电线路,由于本文讨论的上述节点间由高电压等级输电网络连接,其线路电阻远小于电抗,因此可以近似认为Yij=jBij;由于线路电抗较大,互电纳Bij很小,后文计算过程中忽略含有Bij的3次和4次乘积项;由于节点导纳矩阵有对角占优性,不对自导纳Yii作上述近似。

2 受端电网静态电压稳定分析
2.1 静态电压稳定临界条件推导
L指标由Kessel等人提出,广泛用于表征和评估系统内的静态电压稳定程度,该指标下系统内的节点被分成两种,分别为负荷节点l和发电机节点g。针对图1所示的包含新能源和直流逆变站等其他节点的多类型节点系统(除负荷节点外节点数为n-1,仍用g表示其集合,图1中n=4),节点电压方程如式(8)所示:
(8)
式(8)第一行可以化为
(9)
L指标即定义为式(9)等号右侧第一项与负荷电压相量比的模值,它是(0,1]内的实数。
(10)
如果负荷节点的电压失稳,则对应节点L值将增大并超过1.0[15]。对于有多个负荷节点的系统,当任何负荷母线变得不稳定时都会发生受端电网电压崩溃。由于L指标需要通过临界情况下的潮流计算获得,故推导与“L=1.0”等价且能够更方便用于判定电压稳定性的解析形式临界条件。根据式(8)可解出:
(11)
考虑一种极端的恶劣拓扑情况,即所有负荷节点的彼此之间的电气距离都很近,此时当任一负荷母线电压崩溃时,其他所有负荷节点的L指标都十分接近1.0,也就说将节点l作为所有负荷节点集合的等效节点,上述假设的物理意义即对应节点l的L指标达到1.0。将式(11)带入式(10),并将L指标取为1.0,可得:
(12)
易观察到式(13)是式(12)成立的充分条件。
(13)
注意到式(13)所示等效临界条件包含n-1阶矩阵的求逆,仍不便于进一步解析形式的分析和计算,考虑通过节点消去(计算量为n-2阶,如对于图1所示4节点系统,计算量从3阶求逆变成2阶求逆),使消去后的系统内仅存在1个负荷节点和1个发电机节点,此时等效临界条件转化为式(14)。
(14)
对比式(13),式(14)中节点消去后的变量以上撇标注。
2.2 新能源极限渗透率计算
定义新能源高比例并网致使负荷节点l电压达到临界稳定时对应的新能源渗透率ρ为新能源极限渗透率,以ρmax表示,可表征受端电网的电压稳定极限。利用式(14)对应的临界条件可以推导ρmax,首先将式(7)按照分块线进行矩阵分块后重写为
(15)

(16)


(17)
将式(17)带入式(14)进行化简,在等式两端取实部,可计算得直流馈入的高比例新能源受端电网静态电压临界稳定的新能源极限渗透率ρmax:
(18)
a、b满足:
(19)
式(18)给出的ρmax偏保守,如果考虑到负荷分布很分散,在某一负荷节点电压崩溃时,所有负荷节点对应的L指标同时到达1.0的发生概率较低。
可计算ρmax对应的新能源的接入容量如下:
(20)
式(20)中a正比于Pl,当Pl可变时,a+b2/a随着Pl增大先减小后增大,因此Pr存在极大值,在a=-b时取得,此时:
(21)
需要指出的是,该条件对应的负荷有功较大,根据附录A,此时负荷有功Pl接近负荷节点的短路容量,一般难以实现。
2.3 新能源极限渗透率的影响因素分析
根据式(18)和(19),分析直流馈入和网络拓扑参数对ρmax取值的影响。
2.3.1 直流馈入的影响

(22)

ρmax<ρmax0的详细证明过程见附录A。该结论表明直流馈入减小了受端静态电压稳定对应的新能源极限渗透率。结论不难理解,新能源高比例并网使缺少火电机组的受端电网变成弱受端电网,在此基础上如果直流馈入,必然会进一步削弱受端电网的强度,使受端的电压稳定性进一步恶化。
2.3.2 网络拓扑参数Bij的影响
设受端电网内所有输电线路单位长度电抗为x,则节点之间的电气距离可用线路长度来衡量,即Bij=1/(lijx),式(18)和(19)可改写为
(23)
式(23)已忽略了含|zh|的较小项,可看出:
(1)对于与新能源节点直接连接的线路llr,减小其长度,ρmax增大;
(2)对于其他与新能源节点不直接连接的线路lgh、lgl、llh,增大其长度,则使a、b增大,因a>0,b<0,a2增大而b2减小,故ρmax增大。
直观上,llr表征新能源与负荷之间的电气联系,而llh等表征其他电源与负荷之间的电气联系,因此只有减小llr,增大llα(α≠r),才能增强新能源对负荷的支撑同时削弱其他电源对负荷的支撑。
3 算例分析

3.1 新能源极限渗透率理论计算
利用表1中数据可计算直流馈入前后受端电网的新能源极限渗透率。
(1)根据式(4)、(18)和(19)计算ρmax:

表1 计算及仿真参数设置
(2)根据式(22)计算ρmax0:
(3)将P1视为变量,可根据式(21)计算Prmax及对应的ρmax:
以上计算过程可以看出新能源极限渗透率由两部分组成,第一部分受直流等效电动势Eh、负荷有功Pl、网络拓扑影响,第二部分受新能源节点自电导Grr影响。结果说明算例参数设置下满足ρmax0>ρmax。同时,新能源节点r的自电导Grr对ρmax具有贡献,该结论与文献[9]是一致的。
3.2 新能源极限渗透率影响因素仿真验证
在PSCAD中搭建了图1所示的仿真模型,以小扰动后电压是否失稳为标准,研究直流馈入、网络拓扑变化对ρmax的影响。需要指出,考虑直流和新能源控制系统以及动态过程,系统失稳点可能发生漂移,因此ρmax不一定与计算值符合,仿真分析目的是验证上述因素对静态电压稳定点的影响。
首先确定系统的静态电压失稳的临界点,将新能源渗透率ρ固定为某一值,待系统稳定1 s后Pr突然增加30 MW,观察节点电压是否失稳。ρ=27.5%~29%时,系统稳定后受小扰动后各节点的电压变化曲线如图3所示。

图3 直流馈入时受端电网受小扰动后的电压变化曲线Fig. 3 The voltage curve of the receiving-end grid after a small disturbance under DC infeed
可以看到ρ=27.5%时系统是稳定的,而ρ≥28%时系统呈现低阻尼特征,电压均经过低频振荡后失稳,因此,ρmax位于区间[0.275,0.28]内,此结论比计算值30.47%偏小2%。还可看到随着渗透率的增大,低频振荡的周期数减小,振荡幅值增大,系统电压失稳速度加快。
仿真验证直流馈入、网络拓扑参数变化对静态电压稳定点的影响。将直流逆变站与节点h断开连接,从ρ=27.5%起以0.5%为步长增加渗透率,观察稳态施加小扰动后各节点电压变化,发现ρ=36%不失稳而ρ=36.5%时失稳,如图4所示。

图4 直流未馈入时受端电网受小扰动后的电压变化曲线Fig. 4 The voltage curve of the receiving-end grid after a small disturbance under DC non-feed
说明直流未馈入时,ρmax0位于区间[0.36,0.365]内,比计算值32.45%偏大4%。ρmax0明显大于ρmax,说明直流馈入会减小ρmax,与前文分析一致。对比图4与图3的电压失稳形式还可发现,电压失稳不再呈现振荡失稳,而是近似于无功补偿不足导致的单调失稳。
取ρ=28%,设置lrl分别减小10 km,增大10、20、30 km,lgl分别减小10、20、30 km,增大10 km一共8个场景,稳态施加小扰动后各场景节点电压变化情况如图5所示。

图5 网络拓扑改变时受端电网小扰动后的电压变化曲线Fig. 5 The voltage curve of the receiving-end grid after a small disturbance under network topology changes
对比图5和图3右上图,可观察到当lrl增大(Δlrl>0)电压失稳加快,lgl减小(Δlgl<0)时,电压振幅增大,说明两场景对应的ρmax减小;当lrl减小(Δlrl<0)或lgl增大(Δlgl>0)时,电压不失稳,说明两场景对应的ρmax增大,因此新能源与负荷节点之间的电气距离越小,其他电源与负荷节点之间的电气距离越大,ρmax越大,与前文分析一致。在实际新能源接入布局中,不考虑负荷自身的消纳能力,为了使新能源接入的渗透率尽可能大,应该让新能源远离常规火电机组并靠近负荷。
4 结 论
为应对未来电力电子化和新能源高比例接入下的受端电网电压稳定问题,本文对直流馈入下的高比例新能源受端电网场景进行建模,以网络代数方程和L指标为基础,推导了表征受端电网静态电压稳定极限的新能源极限渗透率ρmax,并研究了影响ρmax取值的因素。结果表明,对于受端电网,直流馈入、增大新能源与负荷节点之间的电气距离、减小其他电源与负荷节点之间的电气距离均会使ρmax降低。后续研究中,将对包含送端的网内交直流混联场景进行建模并研究满足电压稳定的最大新能源极限渗透率和并网容量,以期获得对跨区域电网协同规划更有借鉴意义的结论。

