宏观交通流模型参数标定方法

邵长桥， 郭 杰， 刘小明

(北京工业大学交通工程北京市重点实验室， 北京 100124)

密度- 速度、密度- 流量、速度- 流量关系被称为交通流基本模型，其在交通流理论研究和应用中具有重要的作用. 一是可以通过建立交通流模型来刻画交通流运行规律，为交通预测和控制提供方法；二是可以根据交通流模型对交通流特征参数进行估计，例如应用基本图模型估计道路设施通行能力、临界速度等[1]，为交通规划和运行分析提供基础参数. 正是鉴于交通流基本模型的重要性，研究人员在交通流模型和模型参数标定方面进行了大量研究，不断地寻求预测或估计精度更高的建模方法. 最早的交通流模型可以追溯到格林息尔治提出的线性密度- 速度模型[2]. 其后，研究人员提出了众多交通流模型，并不断用观测数据对交通流模型进行验证，以选择出更好的模型[3-12]. 一方面，研究人员通过引入更多的参数来提高模型的灵活性和适用性，如Van Aerde等[10]在速度- 车头间距(密度)模型中引入了4个参数，Wang等[11]在密度- 速度曲线模型中引入了5个参数. 另一方面，研究人员对单结构模型提出了质疑，认为其不能同时刻画非拥堵和拥堵状态下交通流特性，并提出了分段的密度- 速度模型[13]，如马晓龙等[14]基于生长曲线原理建立了Logistic密度- 速度关系模型，并应用实测数据对模型参数进行了标定.

然而，交通流模型对数据拟合不充分的原因不仅仅是模型选择的问题，还与模型参数估计方法以及观测数据特征有关[13-16]. Qu等[15]认为用最小二乘方法来估计模型参数会忽视观测数据“样本”分布不均衡性对模型参数估计影响，提出了加权最小二乘估计方法，并进一步指出了模型与数据拟合程度不理想不仅仅是模型问题，也与观测数据分布和估计方法有关. 张辉等[16]和林豪等[17]从提高模型对观测数据拟合的角度，分别应用k均值聚类最小二乘方法与层次聚类最小二乘法来提高模型估计精度，研究结果说明了模型对数据拟合程度不仅与模型有关，还与参数估计方法有关. Rakha等[18]考虑了流量、速度、密度3个基本变量的观测误差，提出了基于全变量偏差平方和最小的估计方法，但没有给出最优解的理论证明，并且该方法需要开发专用算法，不便于推广和应用. Shao等[19]综合考虑了因变量和自变量的观测误差，对Van Aerde模型[10]进行了修正，并给出了模型参数的极大似然估计方法，验证了新模型对观测数据具有更高的拟合精度. Zhang等[20]在Qu等[15]的工作基础上，提出了对样本数据重构的方法来克服观测数据不均衡性对单段交通流模型参数估计的影响. Zhang等[21]同样考虑速度、密度观测数据的不均衡性对密度- 速度关系模型参数估计的影响，提出了应用排序重构样本的方法对模型参数进行了标定. Neila等[22]考虑了拥堵和非拥堵状态下交通数据的散布情况,提出了基于数据特征的交通流基本图模型参数标定方法.

通过文献查阅发现，已有的宏观交通流模型以及参数估计更多地考虑了单一模型(即密度- 速度、密度- 流量和速度- 流量关系模型中的一个)的估计精度问题[15-20]，仅有少数的文献注意到三者之间的内在关系对模型参数估计的影响[23-24]，特别是其衍生模型估计和预测精度下降问题. Duncam[23]注意到了基于经验的密度- 速度关系模型变换得到的速度- 流量模型存在拟合精度下降现象问题，但没有给出解决方法. Castillo[24]在对密度- 速度模型参数标定时，考虑了密度- 流量模型拟合优度问题，但没有对模型参数估计效果进行论证；没有考虑速度、流量的量纲对模型参数估计的影响. 正是鉴于上述问题，本文假定速度、流量、密度中一个变量为自变量，另两个变量为因变量，提出了联合模型参数估计方法，构造了优化目标函数，并基于Castillo-Benítez、Van Aerde模型和实测数据验证了联合模型参数估计方法可提高模型对实测数据的拟合精度.

1 问题的描述

为了刻画交通流动态特性，Lighthill、Whitham和Richards根据流体力学理论和流量守恒定律提出了著名的LWR模型[25-26].

(1)

并且满足基本关系式

q=k·v

(2)

式中：q为流量，辆/h；k为密度，辆/km；v为区间平均速度.

研究表明，连续流设施的交通流存在平衡状态[9]，其速度- 密度关系可以用连续函数[2-11]表示

v=f(k,β)

(3)

式中：f(k,β)为密度函数；β为模型参数(或参数向量).由式(2)(3)可以得到密度- 流量关系式

q=f1(k,β)

(4)

式中f1(k,β)=k·f(k,β).在实际应用中，往往会出现这样的问题：由观测数据(ki,vi)(i=1,2,…,n)估计理论模型(3)中参数β(其估计用表示)，把代入模型(4)可得到的经验模型q=f1(k,)，但q=f1(k,)对实测数据拟合程度较低.其主要原因是是基于速度- 密度(v-k)关系模型估计的，并没有考虑密度- 流量(q-k)关系.

由式(3)可得到速度- 密度关系模型：k=f-1(v,β)(f-1(·)为f(·)的逆函数)，把其代入式(2)则可得到记q=v·f-1(v,β).记f2(v,β)=v·f-1(v,β)，则速度- 流量(q-v)模型可表示为

q=f2(v,β)

(5)

2 联合模型参数估计方法

传统的交通流模型参数标定主要是采用最小二乘法(包括非线性最小二乘法)，优化目标为因变量观测数值与其估计值的总偏差平方和最小.为了叙述的方便，本文先介绍单一模型优化目标函数，然后再给出联合模型优化目标函数的构造方法.

2.1 单一模型优化目标函数

单一模型参数优化目标函数法就是选择式(3)(4)或式(5)中的一个模型对参数标定，然后应用q=k·v求出另外1个或2个关联模型.根据自变量和因变量的选择，可分为以下3种情形.

1) 流量总偏差平方和最小

一般用于速度- 流量或密度- 流量宏观模型参数估计.模型假设速度v或密度k为自变量，交通流量q为因变量，其优化目标和约束条件为

(6)

s.t.qi=f1(ki,β),i=1,2，…,n

(7a)

或

s.t.qi=f2(vi,β),i=1,2,…,n

(7b)

式中：qi、i分别为流量的第i观测值与估计值；ki为密度的第i观测值；vi为速度的第i观测值；f1(·)、f2(·)分别为密度- 流量函数、速度- 流量函数；β为模型参数.应用式(6)作为优化目标，其假设误差主要来自于因变量q，而自变量v或k是可精确测量或测量误差是可忽略的.

2) 速度总偏差平方和最小

一般用于流量- 速度或密度- 速度宏观模型参数估计.模型假设k或q为自变量，v为因变量，基于最小二乘法的参数估计优化目标函数和约束条件为

(8)

s.t.vi=f(ki,β),i=1,2,…,n

(9a)

或者

(9b)

式中：vi、i分别为速度的第i观测值与估计值；f(·)、f2(·)分别为密度- 速度函数、速度- 流量函数；β为模型参数.

同样，应用式(8)作为优化目标，则只考虑了因变量v的观测误差，而忽略了自变量k或q的观测误差.

3) 密度(车头间距)总偏差平方和最小

该方法常用于标定基于跟驰理论导出的速度- 密度关系模型[19]，其假设密度(或车头间距)为因变量，速度为自变量.优化目标函数和约束条件为

(10)

s.t.ki=f-1(vi,β),i=1,2,…,n

(11a)

或

(11b)

式中ki、i分别为密度的第i观测值与估计值.

单一模型参数优化方法的特点是模型中只有一个自变量和一个因变量，并假设误差主要是来自于因变量.其优点是模型参数标定方法相对简单，其不足是参数估计过程忽略了变量之间关联性，没有考虑衍生模型或变换模型的估计精度[24].

2.2 联合模型参数优化目标函数

针对单一模型参数优化方法存在的不足，可考虑联合模型参数优化方法.例如，文献[26]假定速度v、流量q是密度k的函数：v=f(k,β)，q=k·f(k,β)，建议对k-v模型v=f(k,β)进行参数估计时，同时考虑k-q模型q=k·f(k,β)的估计精度.根据速度、流量、密度三者关系以及模型参数估计需要，构建联合模型参数优化目标函数

(12a)

s.t.vi=f(ki,β),i=1,2,…,n
qi=f1(ki,β)

或

(12b)

s.t.vi=f(ki,β),i=1,2,…,n
qi=f1(ki,β)

或

(12c)

或

(12d)

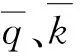
式(12a)和式(12b)是把密度作为自变量，流量和速度作为因变量，采用了2个因变量总的偏差和作为优化目标；式(12c)和式(12d)采用了2个因变量总的偏差和的几何平均值为优化目标，在后文中会发现，可利用式(2)对式(12a)和式(12b)进一步化简.式(12a)和式(12c)没有考虑不同变量量纲的影响，式(12b)和式(12d)考虑了数据量纲的影响.同样，以速度作为自变量，流量和密度作为因变量来构造联合模型参数优化目标函数.

注意到qi=kivi和i=kii，式(12d)可进一步表示为

(13)

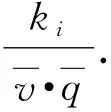
从上面给出的优化目标函数可发现，式(6)～(10)是以单个交通流变量估计精度作为模型参数估计准则，没有考虑密度、速度、流量3个变量之间的相关性；式(12a)～(12d)以2个交通流变量估计精度作为模型估计准则，考虑了流量、速度、密度三者之间的关联性.特别地，优化目标函数式(12d)可以结合加权最小二乘方法对模型参数进行估计.

同样的方法可以以速度为自变量，流量和密度为自变量构造优化目标函数，其将在案例分析中介绍.

3 案例分析

3.1 模型和优化目标函数选择

本研究以Castillo-Benítez模型[9]和Van Aerde模型[10]参数标定为例来说明单一模型、联合模型参数优化方法对模型估计精度的影响.Castillo-Benítez模型首次引入了阻塞波波速来刻画拥堵对交通流的影响而受到关注[9]，Van Aerde模型概括了Greenshields模型和Pipes模型的优点，并适用于刻画不同的交通设施的交通特性[27].

Castillo-Benítez密度- 速度模型[9]为

(14)

式中：vf为自由流速度，km/h；kj为阻塞密度，辆/km；wj为阻塞波波速，km/h.根据模型式(14)的特点，采用联合模型参数优化目标函数

(15a)

s.t.qi=kii,i=1,2,…,n

正如前所叙述，式(15a)可进一步表示为

(15b)

(15c)

Van Aerde模型[10]为

(16)

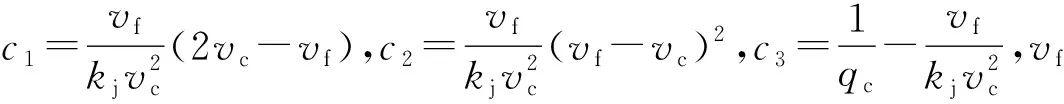
(17a)

s.t.i=ivi,i=1,2，…,n

(17b)

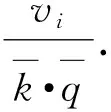
(17c)

根据上边的论述，模型(14)与模型(16)的优化目标函数分别为式(15c)和式(17c)，可以采用模型变换的方式，将问题转化为非线性最小二乘估计问题.

3.2 优化效果评价方法

在回归分析理论中，常用判定系数R2来度量模型对观测数据的拟合程度，R2值越大，说明模型对观测数据拟合程度越好.为了说明联合优化函数式(15a)和式(17a)或式(15b)与式(17b)对模型拟合效果的影响，本研究应用加权判定系数度量模型拟合优度，定义加权判定系数为

(18)

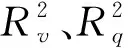
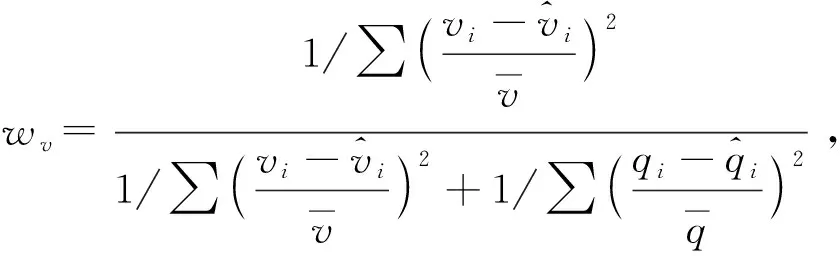
(19)

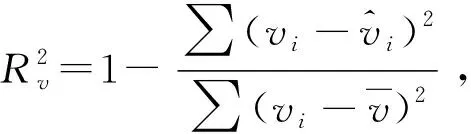
(20)

式中：vi、i分别为速度观测值和估计值，km/h；qi、i分别为流量观测值和估计值，辆为实测速度均值，为实测流量数据的均值，辆/h.

判定系数度量了模型对观测数据的拟合程度.为了进一步量化模型估计精度，并考虑到交通流观测数据的随机性，本文同时应用平均相对误差(mean absolute percentage error,MAPE)和平方根误差(root mean squared error,RMSE)来度量观测值和估计值差异[28]，式(21)、式(22)分别给出了流量估计的平均相对误差估计和平方根误差计算公式.

(21)

(22)

同样，可以给出速度、密度估计的平均绝对百分比误差和平方根误差.平均绝对百分比误差越小，说明模型对变量估计精度越高.

3.3 结果分析

为了比较单一模型和联合模型参数优化方法对交通流宏观模型参数估计的影响，分别应用实测数据对Castillo-Benítez和Van Aerde模型进行参数估计.所用数据由北京市交通管理局提供，其为北京市西二环路官员桥附近主路微波检测数据.数据采集时间为2017年11月13—15日，数据采集间隔为2 min.应用SAS软件[29]中的非线性回归分析模块中的Levenberg-Marquart方法对模型参数进行了估计，为了说明联合模型估计效果，同时也给出了单一模型参数估计结果.表1、2分别是2个模型采用单一模型、联合模型参数优化方法给出的模型参数估计结果.

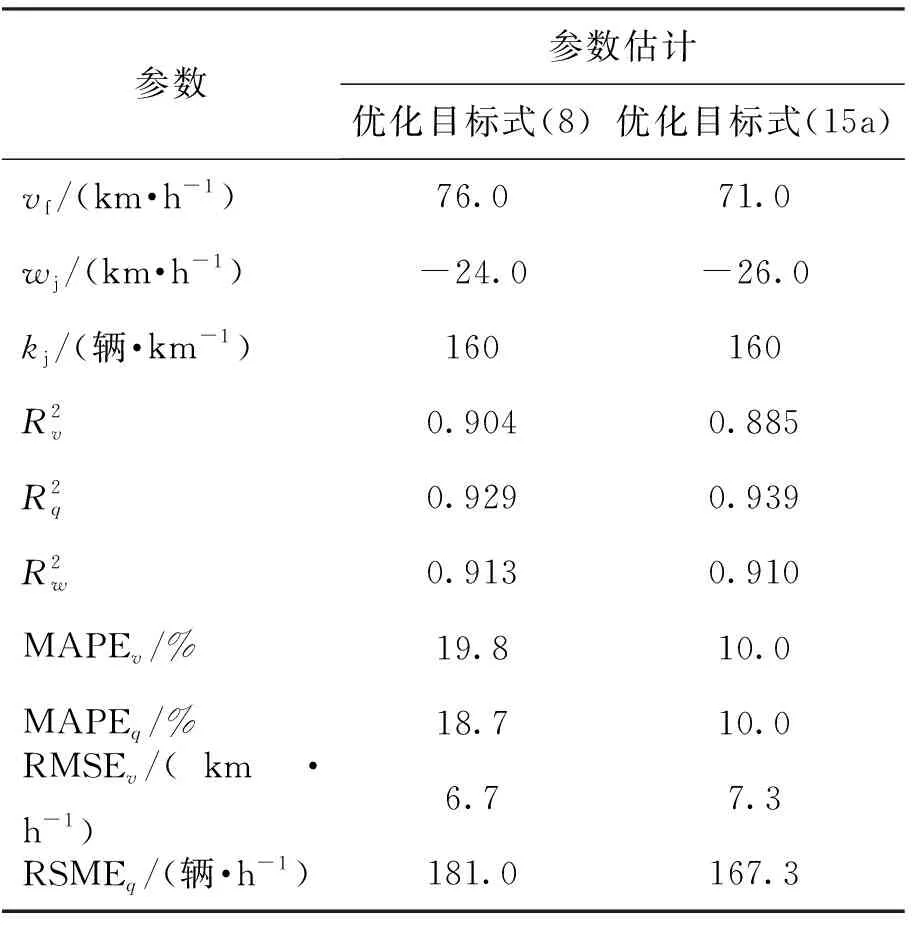
表1 Castillo-Benítez模型参数估计结果比较

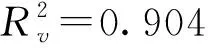
2) 对于Castillo-Benítez模型而言，单一模型优化结果对应的速度估计与流量估计MAPE分别为19.8%和18.7%，速度和流量估计的RMSE分别为6.7 km/h和181.0辆/h；相应的联合模型优化计算的速度和流量估计MAPE为10.0%和10.0%，速度和流量估计的RMSE分别为7.3 km/h和167.3 辆/h.因此，对于Castillo-Benítez模型而言，联合估计在一定程度上牺牲了原来单一模型给出的速度估计精度，但提高了流量估计精度，速度的RMSE从6.7 km/h提高为7.3 km/h，流量RMSE从181.0 辆/h减少到167.3 辆/h.

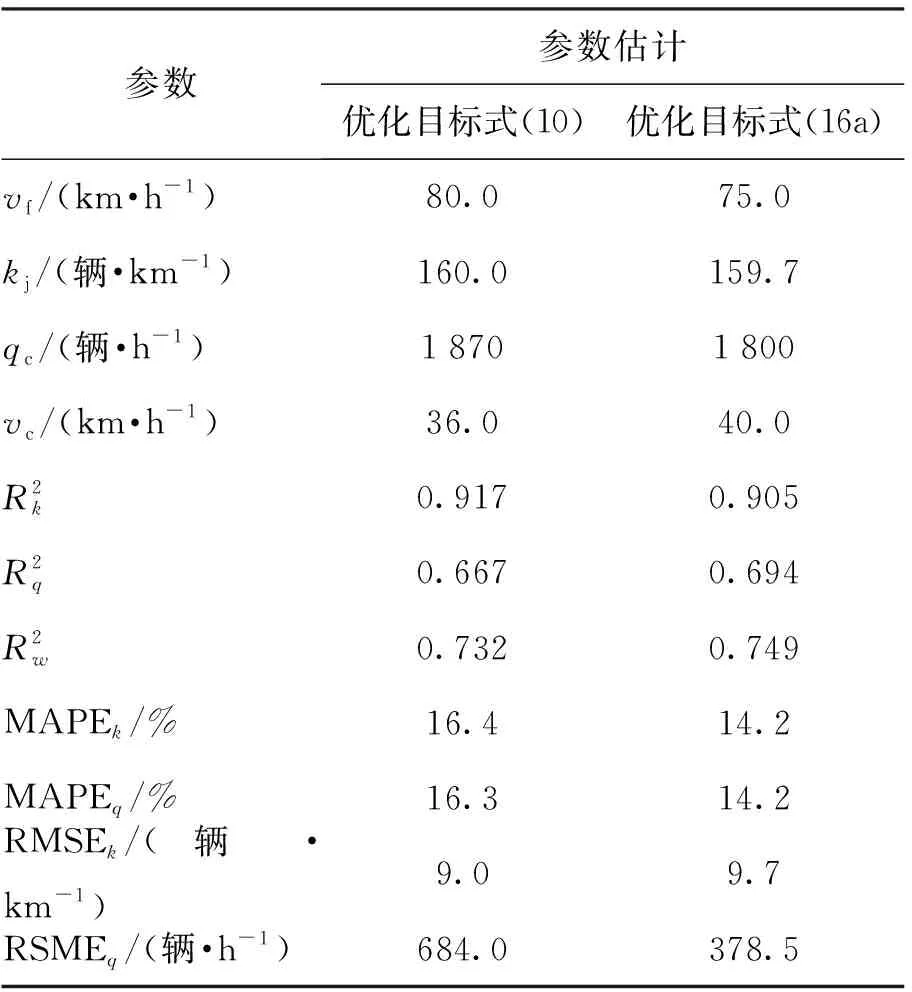
表2 Van Aerde模型参数估计结果比较

3) 图1给出了基于标定的Castillo-Benítez模型估计的交通流参数与实测数值散点图.其中，图1(a)和图1(b)是基于单一优化模型估计得到的速度和流量估计值与实测数值散点图，可以发现估计值与实测值拟合程度并不理想；图1(c)和图1(d)分别是应用联合模型计算的速度和流量估计值与实测数值散点图；图1(e)和图1(f)分别是应用单一模型与联合模型计算的密度- 速度、密度- 流量估计值与实测数值对比散点图.由图1可以发现，相对于单一优化模型估计而言，联合模型优化方法得到的估计值与实测值拟合程度改善明显，特别是对于高密度交通状态下，联合估计结果与实测数据更接近.

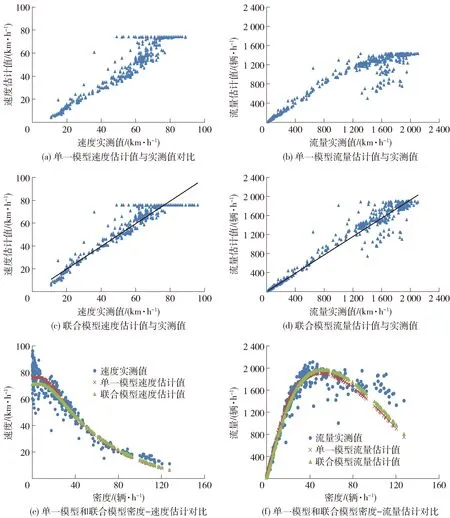
图1 基于Castillo-Benítez模型的变量估计值和实测值散点图Fig.1 Plots of field data and estimated value from Castillo-Benítez model

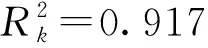
5) 对于Van Aerde模型而言，单一模型优化法计算的密度和流量MAPE分别为16.4%和16.3%，密度和流量估计的RMSE分别为9.0辆/h 和 684.0辆/h；联合模型优化法计算MAPE值为14.2%和14.2%，密度和流量估计的RMSE数值分别为9.7 辆/km和387.5 辆/h.因此，对于Van Aerde模型而言，联合估计在一定程度上“牺牲”了原来单一模型给出的密度估计精度，密度RMSE从9.0 辆/km提高为9.7 辆/km，但提高了流量估计精度，流量RMSE从684.0 辆/h减少到387.5 辆/h.

6) 图2给出了基于标定的Van Aerde模型估计的交通流参数与实测数值散点图.其中，图2(a)和图2(b)分别为单一模型优化法估计的密度和流量值与实测值散点图，图2(c)和图2(d)分别为联合模型优化法估计的密度和流量值与实测数值散点图，图2(e)和图2(f)分别是应用单一模型与联合模型计算的速度- 密度、速度- 流量估计值与实测数值对比散点图.由图2可知，相对于单一模型而言，联合模型参数估计值与实测值拟合程度稍有改善，但与Castillo-Benítez模型估计结果不同的是，对于非拥堵状态下，联合模型估计结果与实测数据更接近.

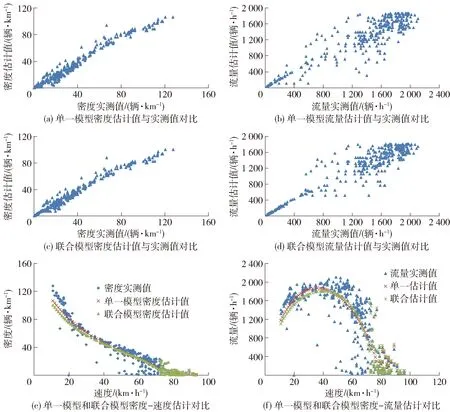
图2 基于Van Aerde模型的变量估计值和实测值散点图Fig.2 Plots of field data and estimated value from Van Aerde model

从以上结果可以发现，对Castillo-Benítez模型而言，联合模型参数估计方法显著提高了流量的估计精度；对于Van Aerde模型而言，模型精度有所提高，参数估计误差有所改善.

4 结论

1) 从联合模型估计精度角度，提出了交通流基本模型联合模型参数估计方法.

2) 研究结果表明，估计联合模型参数估计方法在一定程度上“牺牲”单一变量估计精度的基础上，但提高了模型整体的估计精度.

3) 从实测数据验证结果来看，模型估计精度的提高与模型选择有关，这也说明了模型选择和参数估计方法影响了模型对实测数据拟合精度.

4) 联合模型估计效果评价指标还需要进一步研究.本研究只讨论了给定的交通流模型以及目标函数形式下模型估计效果，没有讨论其他交通流模型以及目标函数，以后的研究中可进一步考虑优化目标、参数估计方法对交通流模型参数估计精度的影响.