循环弯曲荷载作用下UHPC疲劳裂纹扩展行为研究

王志云,方兆麟,陈思可

(1.广东粤海珠三角供水有限公司，广州 511455；2.广州市花都区灌区管理中心， 广州 510800；3.广东省水利水电科学研究院，广州 510635 4.广东省水利新材料与结构工程技术研究中心，广州 510635)

1 概述

随着建筑材料的进步，超高性能混凝土(UHPC)在建筑结构发展中的应用越来越广泛。大多数此类结构在循环荷载条件下运行，因此，疲劳裂纹可能会引发和扩展，可能导致灾难性事故[1]。因此，结构设计需研究循环荷载下UHPC中的裂纹扩展行为。

已有研究定性地描述了UHPC的裂纹扩展行为。文献[2]建立了裂纹扩展与疲劳寿命之间的关系，将疲劳寿命分为3个阶段：(Ⅰ)裂纹萌生；(Ⅱ)稳定裂纹扩展；以及(Ⅲ)断裂失效。文献[3]证明了裂缝的宽度、高度和数量的演化也可以大致分为3个阶段。文献[4-5]描述了弯曲循环荷载下每个阶段的裂纹演变：第1阶段，没有出现可见裂纹；第2阶段，原生裂纹没有改变，但出现了一些新裂纹并扩展。随着时间的推移，主裂纹定位并迅速发展，而其他裂纹变得更小，直到完全闭合。文献[6]对每个阶段的周期进行了量化，报告称第1阶段占疲劳寿命的15%，而第2阶段占75%，第3阶段占剩余的10%。文献[7]提供了不同损伤阶段裂纹模式(形状、数量和宽度)的更详细数据。文献[8]分析了UHPC中的裂纹分布，得出疲劳裂纹更可能出现在应力集中区域，其结果成功地描述了在循环荷载作用下UHPC中观察到的裂纹发展。为了更好地理解疲劳的基本原理，应对裂纹扩展现象进行理论研究。

因此，本研究目的是定量描述含有不同纤维体积分数(0.5%、1.0%、1.5%和2.0%)的UHPC在不同应力水平(S=0.80、0.75、0.70和0.65)下的疲劳裂纹扩展行为。通过记录施加的荷载和位移数据，确定了UHPC的柔度。采用数字图像(DIC)技术表征了疲劳裂纹尖端裂纹口张开位移(CMOD)、裂纹长度和局部应变场的演化过程。通过对数据进行拟合，得到了疲劳裂纹长度与加载循环次数的函数关系式，并将裂纹扩展速率确定为该关系式的一阶导数。

2 原材料与试验方法

2.1 配合比设计与试验制备

UHPC中各组分的配比如表1所示。硅粉的SiO2含量为98%，平均粒径为0.2 μm。为了使混凝土更加密实，使用了2种不同尺寸的砂(0.16～0.315 mm和0.63～1.25 mm)。UHPC中的水灰比为0.16，聚羧酸高效减水剂的含量固定在3.5%，固体含量约为30%。使用4种不同体积分数(0.5%，1.0%、1.5%和2.0%)的钢纤维(长度=13 mm，直径=0.2 mm)。用于弯曲疲劳试验和静态弯曲试验的试样尺寸为100 mm×100 mm×400 mm，为了避免疲劳试验期间潜在的强度增加，所有试样水养90 d。

表1 超高性能混凝土配合比 kg/m3

2.2 疲劳试验

每批UHPC样品包含7根梁，对其中3根梁进行了测试，以测量静态弯曲强度并确定循环弯曲试验期间施加的适当应力幅度。对其余4根梁进行测试，以测量弯曲疲劳强度。在100 kN的MTS试验机使用了跨度为300 mm的4点弯曲装置(如图1所示)。在静态弯曲试验中，对试样施加0.2 mm/min的恒定位移速率，而在弯曲疲劳试验中，施加恒定的循环载荷振幅。恒幅载荷以8 Hz的频率作为正弦波形施加。加载首先达到平均值(Pmax+Pmin)/2，然后在最大和最小值范围内循环。疲劳试验在不同应力水平下进行，S=Pmax/Pf(Pmax=最大疲劳应力，Pf=静态弯曲强度)，范围为0.80至0.65。在整个疲劳试验过程中，应力比R=Pmin/Pmax=0.1。含有0.5%、1.0%、1.5%和2.0%纤维体积分数的UHPC试样的静态弯曲应力分别为42.31 kN、54.47 kN、58.42 kN和69.05 kN(如表2所示)。通过试验机的循环计数器测量失效循环次数，选择了200万次加载循环的上限，当试样发生破坏或达到该上限时终止试验。

图1 数值相关法试验装置示意

表2 静态最大弯曲荷载

2.3 数字图像分析法

数字图像分析法(DIC)是一种稳定、无接触、无损的技术，用于测量物体表面的位移。使用2台高分辨率数码相机拍摄样本变形的数字图像，并使用软件处理图像并计算相应的变形分布(如图1所示)。该系统由2个400万像素的摄像头组成，最大图像分辨率为1.05 Mpx(1 024×1 024像素)，摄像头的相对角度为30°。

为了实现精确的测量，对每个试样喷涂随机黑白散斑的高对比度图案。观测区的尺寸为100 mm×200 mm。在试验期间，安装在刚性架上的两个蓝光用于照亮试样，并缓解环境光的变化(图1)。为了在每个加载循环中获取2个图像(1个在最大负载下，1个在最小负载下)，需要1个略高于正弦负载频率的DIC频率。因此，2台摄像机以10帧/s的频率拍摄每个样本的斑点目标区域的图像。

3 结果与讨论

3.1 疲劳裂纹扩展参数的确定

3.1.1最大CMOD和循环比

为了研究UHPC试样的疲劳裂纹扩展行为，在循环弯曲试验期间，通过DIC获得了疲劳裂纹的演化和变形模式。图2展示了CMOD在最大负载(Pmax)下随着循环次数(N)和循环比(N/Nf)的增加而发展。从曲线的形状可以看出裂纹扩展行为的3个阶段：Ⅰ)快速发展；Ⅱ)稳定发展；Ⅲ)失效阶段。为了清楚地观察每个阶段的裂纹演变，图3显示了SF1.5(S=0.65)在每个阶段结束时的裂纹扩展图像。

图2 “归一化”最大裂缝开口位移和循环寿命的关系示意

图3 裂缝扩展过程中试样表面位移场和应变场演变示意

随着应力水平从0.80降至0.65，疲劳曲线的第1阶段变得更平坦。第2阶段的曲线斜率也降低，疲劳寿命显著提高。随着应力水平的降低，在第3阶段的曲线中观察向上弯曲部分更平滑、更圆的形状，并且在更高的CMOD下发生失效。结果表明：较低的荷载水平会导致更脆的破坏，并且在之前的纤维增强混凝土(FRC)疲劳弯曲荷载下的研究中也观察到了类似的行为[9]。更高的应力水平可能会通过纤维的持续拉出而导致失效，从而产生韧性轮廓。此外，较小的荷载应力水平可通过形成微裂纹促进纤维-基体界面的逐渐弱化[10]。一般来说，在相似的应力水平下，纤维体积分数较高的试样表现出更好的变形能力。然而，在给定纤维含量的试样中，变形能力随着疲劳应力水平的降低而降低，这是因为出现的裂纹较少[3]。

3.1.2疲劳应变分析

为了阐明UHPC在不同加载循环下的应变分布，在不同循环过程中采集了数千张斑点试验区域的图像进行分析。疲劳裂纹的开始主要由最大疲劳应力控制。在4点弯曲疲劳载荷下，试样中心区域的应变局部化导致裂纹萌生。DIC系统记录试件表面的整体和局部应变场。选择在3个阶段的每一阶段结束时获得的3幅代表性图像，检查应变分布的变化。

图4中的应变示意并未表明试样SF0.5和SF1.0在加载过程中沿y方向的开裂行为发生显着变化。表明钢纤维在x方向上的应力传递缓慢。这是由于应变/应力传递网络的不完整，导致应变水平延伸的过程和发展不能有效地传递相邻区域。因此，SF0.5和SF1.0的裂纹行为不是由剪切引起的，而是由张开张力裂缝控制的[10]。然而，在较高的纤维体积分数下，梁底部出现了更显着的应变集中，并形成了许多裂缝。随着循环载荷的进行，试样SF1.5和SF2.0的应变示意表现轻微但明显的45°的发展趋势，表明断裂取决于弯曲破坏。第3阶段结束时，所有试样都出现了主裂纹，而在其他裂纹中未观察到显着变化。

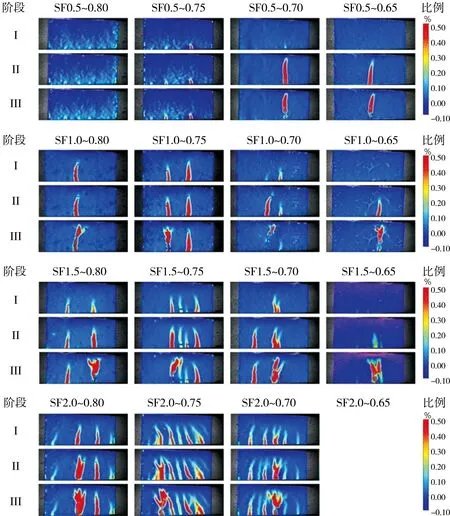
图4 不同应力水平下超高性能混凝土试样表面裂缝扩展及应变场演变示意

3.1.3裂纹长度和加载周期

图5显示了在不同应力水平(S=0.80、0.75、0.70和0.65)下测试的所有试样的裂纹长度与加载循环次数的关系示意。 在循环加载初期，初生裂纹迅速扩展。 随着加载循环次数的增加，裂纹扩展达到稳定状态，因为纤维桥接区有效地抵御了裂纹尖端应力场，并通过在裂纹面之间传递应力来减少裂纹扩展[11]。在循环加载结束时，疲劳损伤随着裂纹长度的突然变化而发生。

S=0.80

S=0.75

S=0.65图5 裂缝扩展长度和疲劳循环次数关系示意

纤维体积分数为0.5%的UHPC试样SF0.5的裂纹长度与循环次数之间的关系不同于其他试样(Vf=1.0%、1.5%或2.0%)。由于其疲劳寿命明显较低，SF0.5的稳态裂纹长度约为20 mm，而其他试样的裂纹长度均约为60 mm。相对于SF0.5，SF1.0、SF1.5和SF2.0试样在各自的曲线中表现出更显著的平稳，表明II期行为的持续时间更长。

3.2 裂纹扩展速率

为了确定裂纹扩展速率，将光滑连续函数拟合到计算的裂纹长度(如图5所示)。建立了以下描述裂纹长度与加载循环次数之间关系的解析函数，并用于提高计算裂纹扩展速率的稳定性和精度[12-14]：

(1)

式中:

a——裂纹长度；

N——加载循环次数；

b、m1、c——试验校准常数。

在图5中，公式(1)可用于精确表示裂纹长度与加载循环次数之间的关系。然后将裂纹扩展速率计算为式(2)的一阶导数：

(2)

图6是裂纹扩展速率(对数标度)与裂纹长度的关系示意，表3所示为试验校准常数。由图6可以看出，最小裂纹扩展速率对应于临界裂纹长度(ac)，其发生在减速和加速阶段之间的拐点处；随着纤维体积分数的增加，最小裂纹扩展速率显著降低。同时，在给定应力水平下，SF0.5试样的裂纹扩展速率高于SF1.0、SF1.5和SF2.0试样；在应力水平为0.70时，SF0.5、SF1.0、SF1.5和SF2.0的最小裂纹扩展速率分别为-3.73、-3.81、-4.14和-4.47。随着应力水平的增加，对于给定的纤维体积分数，裂纹扩展速率增加，SF0.5试样在不同应力水平(S=0.80、0.75、0.70和0.65)下的最小裂纹扩展速率分别为 -2.51、-3.51、-3.73和-3.98。在减速阶段，随着纤维体积分数的增加，裂纹扩展速率的斜率逐渐增大；在加速阶段，随着纤维体积分数的增加，裂纹扩展速率的斜率逐渐减小。

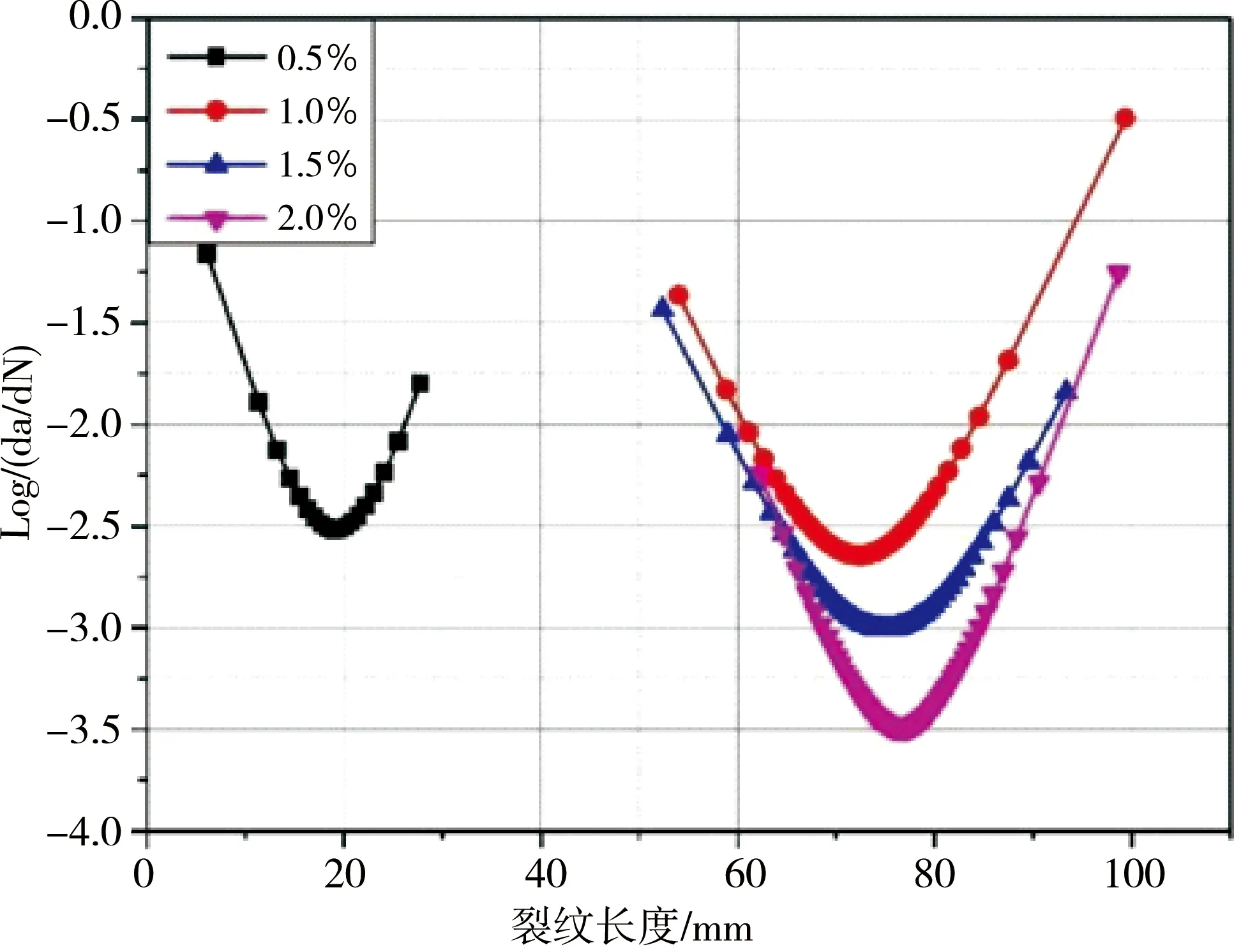
S=0.80

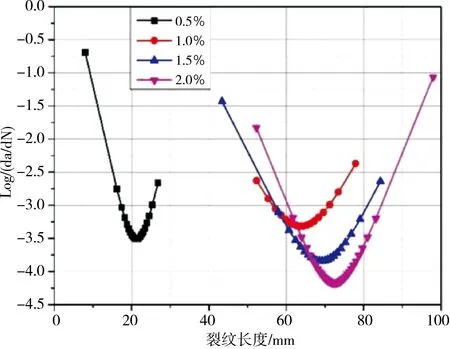
S=0.75

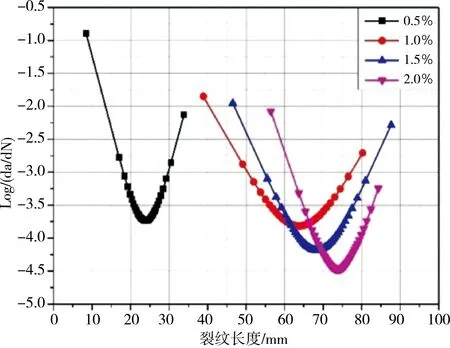
S=0.70

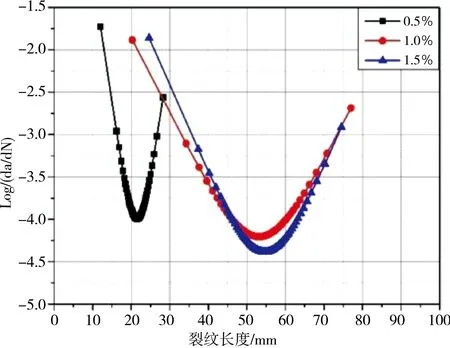
S=0.65图6 不同应力水平下裂缝扩展速率和裂缝扩展长度关系示意

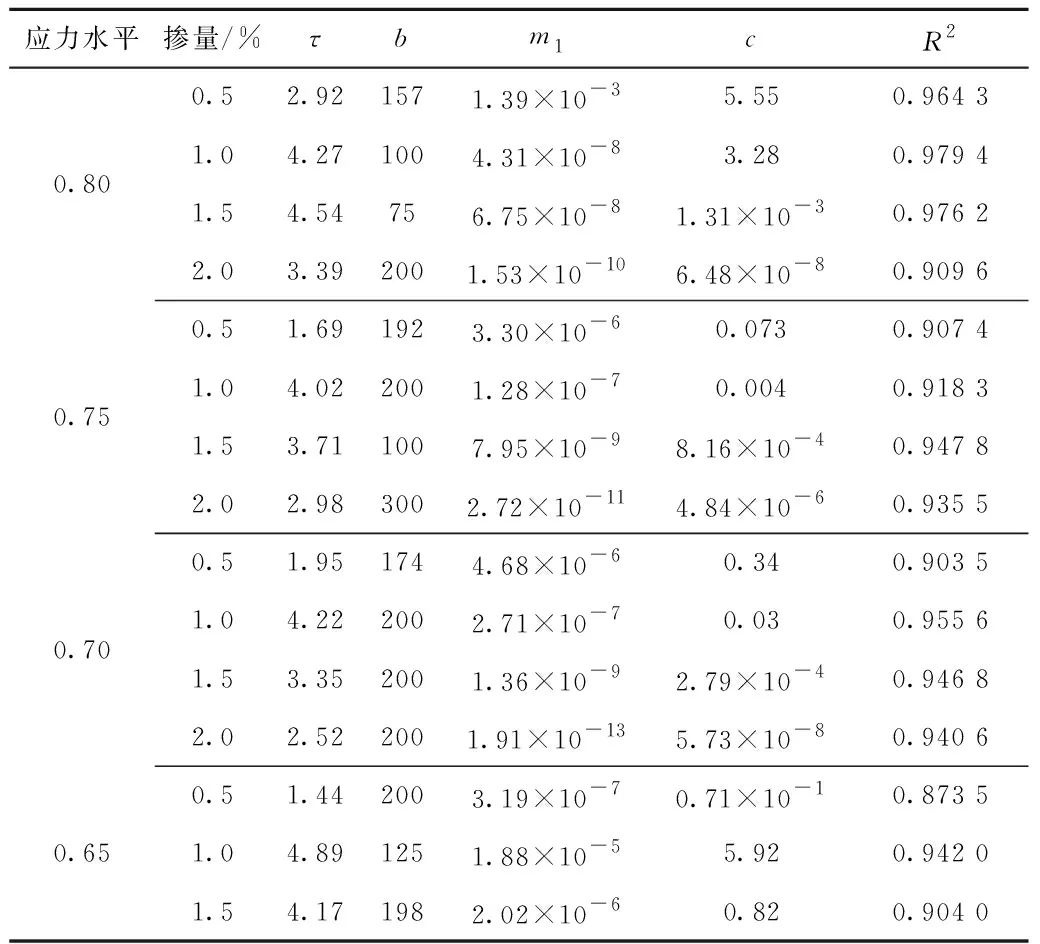
表3 试验修正系数

4 结语

本文研究了不同体积分数的钢纤维和应力水平对UHPC疲劳裂纹扩展行为的影响。利用Paris法则和非线性断裂力学对疲劳裂纹扩展速率进行了理论研究,得出以下结论：

1) 在相同的应力水平下，纤维混凝土试件的疲劳寿命和柔度随钢纤维体积分数的增加而增加。随着应力水平的降低，在不同纤维含量的UHPC试样中观察到类似的发展趋势。

2) 在CMOD和加载循环次数之间的绘制关系中，疲劳裂纹扩展的3个阶段非常明显：(Ⅰ)快速发展;(Ⅱ)稳定发展;以及(Ⅲ)失效阶段。表征阶段I的载荷循环比占疲劳寿命的5%～10%，而阶段Ⅱ和Ⅲ所占的比例分别为70%～85%和10%～20%。

3) 应变图未显示SF0.5和SF1.0中沿y方向裂纹扩展的明显变化。因此，描述这两个试样的破裂模型可能受张开拉伸裂纹机制控制。在SF1.5和SF2.0中，y方向应变图显示45°方向应变集中，表明试样的断裂取决于弯曲破坏。

4) 在循环加载的早期阶段，主裂纹以快速的方式扩展。随着加载循环次数的增加，裂纹扩展达到稳定状态。循环加载结束时，裂纹长度发生突变，导致疲劳损伤。