页岩储层微观结构非均质性图像法定量表征
荆 玥,刘登科
(西安交通大学,陕西西安 710000)
非均质性是油气储层内在固有属性,页岩储层的微观非均质性影响了储层的各项物性、孔隙分布以及矿物分布等。我国陆相页岩微观结构差异较大,有机质与无机矿物的分布呈纹层、似层状以及分散等分布结构,具有极强的非均质性[1]。
页岩储层的微观非均质性表征依赖测量方法,国内外研究者利用铸体薄片[2]、扫描电镜[3]、微纳米CT[4]等图像技术定性描述不同类别的储层微观结构,或者利用低温氮气吸附[5]、二氧化碳吸附[6]、高压压汞[7]等流体注入实验定量计算分析储层的矿物、孔隙分布、含油气性等差异。但是,基于图像法定量表征页岩储层微观结构非均质性的研究较少。本文基于图像处理矿物识别技术定量研究页岩储层微观结构的非均质性,以期丰富储层微观结构非均质性研究方法。
本文首先研究页岩储层微观结构对岩石薄片图像特征参数的影响,其次进行了特征参数的筛选与降维,最后定量分析页岩样品的微观结构类型。
1 图像处理及参数提取方法
在页岩储层的研究中,铸体薄片鉴定、场发射环境扫描电镜、微纳米CT 扫描等图像技术能直观可视研究储层性质。本文选取鄂尔多斯盆地三叠系的延长组长7 页岩气储层的薄片图像数据进行分析,16 组薄片图像按照矿物微观结构被人工划分为分散状、层状以及块状分布等三种类型(图1)。本节首先介绍薄片图像的矿物识别分割处理方法,之后介绍矿物结构非均质性及纹理特征参数的提取方法。
1.1 图像分割处理
页岩薄片的彩色图像中每个像素由0~255 范围的RGB 三个分量组成,对这三个分量使用加权平均法计算可得到像素灰度值,所得灰度图像见图1d~f。通常灰度图像选取合适的阈值可分割出感兴趣的研究区域进行下一步分析,但是页岩薄片图像的消光特征使得不同角度下矿物的灰度差异过大,在研究矿物微观结构时灰度阈值分割并不准确。
矿物识别分割可以提高图像分析的精度,本文使用开源工具包ilastik1.3.3 对研究区的16 个薄片图像进行矿物识别,ilastik 工具包使用随机森林算法基于页岩图像中不同矿物的颜色、强度及纹理等特征在不同的尺度上计算每个像素属于几个类之一的概率。使用工具包的像素分类工作流可以获得较理想的页岩微观结构图像(图1j~i),同时,之后进行特征参数提取工作时还可以将分割图像进行二值化处理,突出微观矿物在有机质中的分布特征。

图1 页岩薄片图像
1.2 图像特征参数的提取
矿物含量的非均质性特征采用代表视域面积与变异系数两种方式描述。
1.2.1 代表视域面积 代表视域面积是一种基于图像数据评价储层非均质性的方法[8],统计从小到大不同尺度下的视域中评价要素所占的比重,当比重稳定时的视域面积就是这种因素的代表视域,代表视域越大,表示该因素非均质性越强。
本文将矿物分布二值化图从9 种路径依次扩大视域,统计相对应路径和边长视域的矿物占视域面积的百分含量,当矿物含量稳定时提取参数。
1.2.2 变异系数 变异系数是数据标准差与平均数的比,可以比较数据离散程度大小,也是评价储层非均质性的方法[3],可以通过水平和垂直两个方向上的变异系数分别描述两个方向上的非均质性,通过式(1)计算水平方向变异系数,式(2)计算垂直方向变异系数:

将矿物在有机质中的分布结构看作图像纹理,通过灰度共生矩阵(Gray Level Co-occurrence Matrix)计算得到薄片图像的纹理特征参数。对于灰度级为L 的图像,通过式(3)可生成L×L 的灰度共生矩阵:
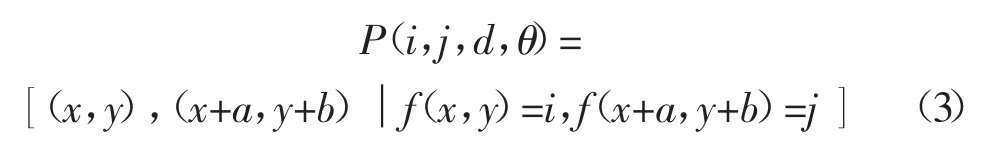
式中:P(i,j,d,θ)-坐标为(x,y)与(x+a,y+b)的像素点,在θ 方向d 距离上出现灰度级组合为(i,j)的频率;θ-灰度共生矩阵的生成方向,一般选取0°、45°、90°、135°进行计算。本节首先将薄片图像分为八个灰度级从灰度共生矩阵提取出对比度、逆差矩、相关性及熵四个纹理特征。
1.2.2.1 对比度 对比度描述像素点与其领域像素的亮度对比情况,它反映了图像中同尺度变化的强烈程度,在页岩薄片图像中,黄铁矿等图像亮度较高的矿物与图象亮度低的有机质之间的递变越多,灰度共生矩阵的对比度越大。
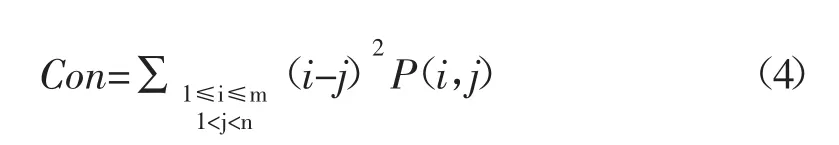
1.2.2.2 相关性 相关性描述了灰度共生矩阵元素在行或列方向上的相似程度,它反映了水平或垂直方向上图像纹理的情况,即如果在某方向上矿物和有机物的纹理越丰富,则此方向的相关度值越大。
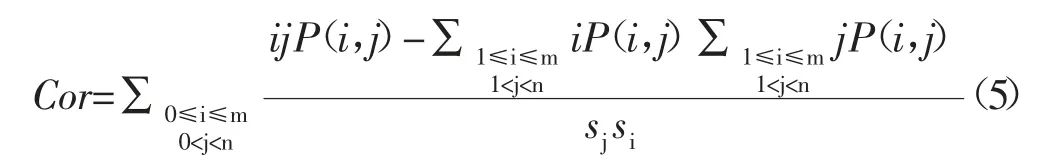
1.2.2.3 逆差矩 纹理逆差矩描述了图像纹理的局部变化,它反映了图像纹理的同质性,在图像的不同区域中的矿物分层结构越像,纹理逆差矩越大。

1.2.2.4 熵 熵度量图像所具有的纹理信息的随机性,它表示了图像中纹理的复杂程度,即图像中矿物分布越分散越复杂,灰度共生矩阵的熵越大。
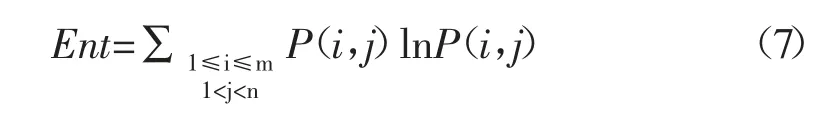
此外,对于二值图像,灰度共生矩阵有特殊的三个参数可以描述矿物的分层结构。对于二值图像,灰度只有两级,所以每个方向上的共生矩阵均为一个2×2 的矩阵。
若将矿物赋值为1,则主对角上的元素分别表示连续的矿物和有机质的个数,副对角元素分别表示矿物与有机质之间的递变。在同尺度下,矿物结构的周长是所有方向上的副对角线元素之和La,该值越大页理发育越复杂。0°和90°方向下的副对角元素之比表征矿物结构的长径比Lc,该值越小矿物结构越扁平。同一方向的副对角元素之差Ld 表征该方向下矿物和有机质的递变程度,该值越大,递变程度越强,且符号代表了递变方向。
2 结果与讨论
2.1 矿物含量的非均质性特征参数的分析
代表视域面积与变异系数两种非均质性特征参数定量矿物含量非均质性特征,结果见图2。由图2 可以看出,代表视域面积参数可以较好的区分层状分布和块状分布,分散状分布的参数值变化范围介于层状与块状参数之间,可见,代表视域面积可部分定量矿物含量非均质性。同时,水平变异系数和垂直变异系数联合应用也可以很好描述块状分布结构在两个方向上的矿物含量非均质性,但是层状分布与分散状分布参数有重合的特征。所以本文选择代表视域面积作为矿物含量非均质性特征参数。
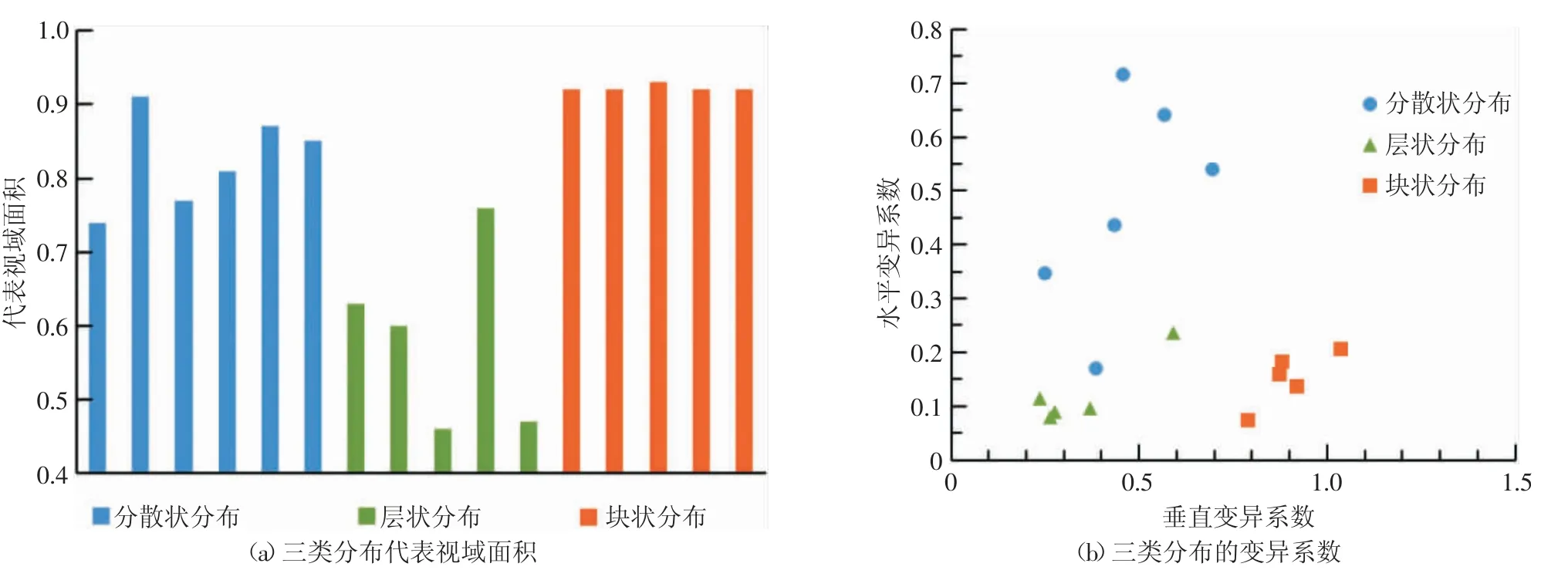
图2 三类分布矿物含量非均质性参数
2.2 纹理特征参数的筛选
上节从图像中提取出7 个可以定量描述矿物分层结构的特征参数,虽然增加特征参数的个数有利于更加全面的描述页岩微观结构的改变带来的图像视觉形态变化,但是,参数维度的增加带来更大的计算量且可能过分关注局部细节,从而造成更大的统计误差,不利于后续的聚类分析,因此需要对上述特征参数进行筛选与降维。
通过对所提取的定量描述矿物分层结构的特征参数之间的相关关系进行研究,得到图3 所示的相关性矩阵图,筛选去除强正相关的参数有利于后续分析,将相关性系数超过0.8 的参数视为强正相关,对比度、逆差矩、周长均与其他参数强相关,因此剔除这三个参数。
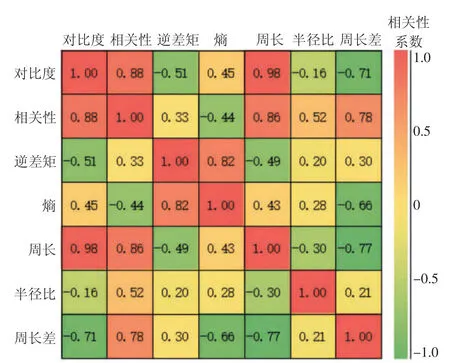
图3 图像纹理特征相关性矩阵图
2.3 特征参数的降维
通过筛选去除极相似的特征参数,得到一个五维向量可以用来表征矿物的分层结构,但是,五维向量在计算中仍然复杂,需要进一步降维。为此,引入主成分分析方法对多维特征向量进行简化。主成分分析方法作为一种经典的降维方法,能够将原来的多个指标重新组合成维度更低的一组互相无关的指标,来衡量图像的特征。
对特征参数之间的协方差矩阵进行特征值分解,可以得到5 个特征值以及对应的特征向量。特征值在特征值总和中所占的比例就是该主成分的贡献率。按照从大到小的顺序排列,具体的贡献率见图4。前两个主成分即可体现出原图像特征向量超过98%的有效信息。采用主成分分析方法将五维向量简化映射到二维向量,降低了多维特征向量的复杂度,可以更加直观地描述矿物分层结构。两个主成分分量通过式(8)计算,形成了一个描述矿物分层结构特征的二维向量。
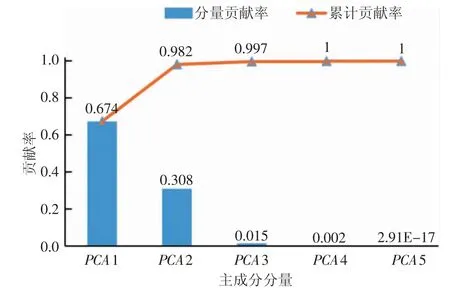
图4 各主成分贡献率
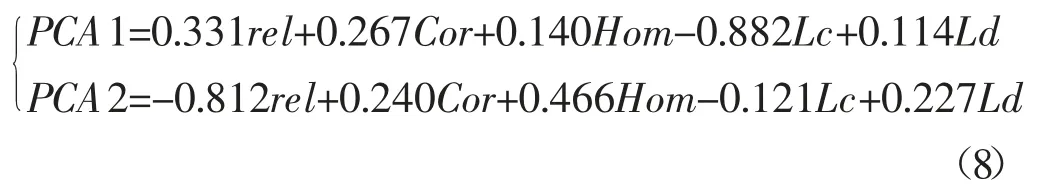
通过计算矿物分层结构特征向量之间的欧式距离,使用最短距离法进行hierarchy 层次聚类,首先将数据中的每个样本看作初始聚类簇,算法运行中找出距离最近的两个聚类簇进行合并,该过程不断重复直到预设的聚类簇个数。通过聚类分析得到三种类型的页岩微观矿物结构。二维向量具有较好的聚类效果,并且聚类结果可以很好的与储层微观结构的人工分类相对应。
3 结论
本文对鄂尔多斯长7 组页岩气储层的微观矿物结构非均质性进行了研究分析,通过提取岩样薄片图像的形状及纹理特征,经过参数降维、定量聚类研究了三种类型的页岩微观矿物结构,具体结论如下:
(1)对于薄片鉴定图像,鄂尔多斯盆地长7 储层页岩的微观矿物结构有分散状、层状以及块状分布三种类型,每种类型在视觉上有较大差异。
(2)对于图像法,代表视域面积作为矿物含量非均质性特征参数比水平和垂直两方向上的变异系数更直接的表征了矿物含量的非均质性。
(3)通过相关系数筛选和主成分降维可以得到量化页岩储层微观结构非均质性的二维向量,使用该向量定量聚类的结果可以有效的与薄片鉴定结果对应。

