基于互补占空比调制的改进全桥ZVS直流变换器

许章茁，潘健

（湖北工业大学电气与电子工程学院，武汉 430068）

近年来，随着政策推新，电动汽车热度不断攀升且发展十分迅速。直流变换器作为电动汽车动力系统中的核心环节受到了广大业内人士和研究学者的重点关注，其中移相全桥直流变换器是较为理想拓扑之一，具有拓扑结构简单、功率密度高且能利用电路自身元件实现零电压开关ZVS（zero voltage switching）等特点，但该变换器仍存在一些劣势，如滞后桥臂软开关范围受限，副边存在占空比丢失以及整流侧存在严重的寄生振荡等问题。

针对上述问题，国内外研究学者提出了一系列解决方案，但由于在传统移相全桥ZVS 直流变换器滞后桥臂开关过程中，仅由谐振电感的储能提供ZVS 条件，导致轻载时ZVS的丢失。为了解决这一问题，主要思路是利用辅助储能元件或施加辅助电路在滞后桥臂开关过程中提供辅助能量。文献[2-4]通过并联无源辅助网络，实现了较宽的软开关范围，但一旦辅助电流源网络的参数确定，其辅助电流幅值与负载无关，重载时过量的辅助能量会增大导通损耗，从而导致变换器效率降低；文献[5]通过并联有源辅助网络，实现了对辅助能量的调控，在大大减小辅助网络带来的额外损耗的前提下保证了滞后桥臂开关的ZVS，且通过合理设计辅助电感，并尽可能减小电路自身的谐振电感以减少占空比丢失问题。占空比丢失是移相调制的特有现象，在一定程度上导致电压增益的损失，为了得到所要求的输出电压，必须减小变压器匝比，但由此导致了通态损耗及副边整流二极管电压应力的增大等问题。为了解决这一问题，主要思路是减小谐振电感以缩短换向阶段，或施加钳位电路以保持副边整流侧的电压[6-7]。由于整流侧的寄生振荡会增大整流二极管的电压应力，影响器件的寿命，同时带来严重的电磁干扰问题，文献[8]通过增设RCD 缓冲电路，吸收整流侧的尖峰电压，但引入的电阻元件会导致额外的损耗，从而降低了变换器效率；文献[9-10]通过增设有源钳位电路，使得吸收电容中的能量回馈至负载，但有源器件的引入增大了电路复杂度，降低了系统可靠性；文献[11-13]通过在原边侧引入钳位二极管网络，在既不使用有损组件也不使用有源器件的前提下消除了寄生振荡。

本文提出了一种基于互补占空比调制的改进全桥ZVS 直流变换器，该变换器能够实现宽范围的ZVS，消除寄生振荡，并能在一定程度上大大减轻占空比丢失问题。首先对传统移相全桥与改进全桥的电路结构以及关键波形进行描述，介绍了改进全桥变换器的创意来源；其次对改进全桥变换器的工作原理与特性进行分析说明；最后通过仿真对比验证了改进全桥变换器的正确性和优越性。

1 电路描述

1.1 基于移相调制的传统全桥ZVS 电路

传统移相全桥ZVS变换器滞后桥臂开关实现ZVS 受负载条件和谐振电感的制约。轻载时，由于谐振电感中的能量不足以提供滞后开关寄生电容充放电的所需能量，因而无法实现滞后开关的零电压开通。通过增大谐振电感可以有效拓宽软开关范围，但会延长移相全桥变换器工作状态中的换向阶段，从而加剧占空比丢失问题。副边整流二极管的寄生电容会与谐振电感产生谐振，导致寄生振荡问题，尖峰电压最大能够达到正常工作电压的2倍，从而增大了整流二极管的电压应力和导通损耗。图1为移相全桥ZVS变换器电路结构及其关键波形。

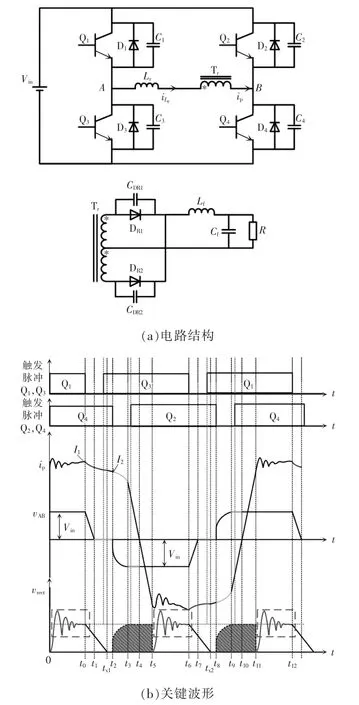
图1 移相全桥ZVS变换器电路结构及关键波形Fig.1 Circuit structure and key waveforms of phaseshifted full-bridge ZVS converter

图1 中：Vin为输入电压；Q1～Q4为主开关管（晶闸管）或其触发脉冲；D1～D4为其反并联二极管（或体二极管）；C1～C4为其寄生电容（或外接电容）；Lr为谐振电感（包括变压器漏感）；为电感电流；Tr为高频变压器；ip为原边电流；DR1～DR2为整流二极管；CDR1～CDR2为其寄生电容；Lf为滤波电感，Cf为滤波电容，R为负载电阻；I1、I2为传统移相全桥ZVS变换器电路的关键电流；vAB为原边电压；vrect为输出电压。

1.2 基于互补占空比调制的改进全桥ZVS 电路

为了使得全桥变换器在轻载条件下仍能保持软开关的特性，减小占空比丢失并抑制整流侧寄生振荡问题，结合文献[1]的非对称脉冲宽度调制APWM（asymmetric pulse width modulation）、文献[5]的并联辅助谐振网络与文献[11]的原边钳位二极管网络，提出了一种基于互补占空比调制的全桥ZVS变换器，其电路结构及其关键波形如图2 所示。

图2中，主开关管Q1/Q3（Q2/Q4）的占空比对应互补，Qa1←La1→Da1与Qa2←La2→Da2是引入的辅助谐振网络，Dc1↔Dc2是引入的原边钳位二极管网络。Qa1、Qa2为辅助开关管（晶闸管）或其触发脉冲；Da1、Da2为辅助二极管；Dc1、Dc2为钳位二极管；La1、La2为辅助电感；ia1、ia2分别为流经辅助电感La1、La2的电流；ia为辅助谐振网络电流（辅助电感电流）；iDc为钳位二极管的网络电流；K为变比。

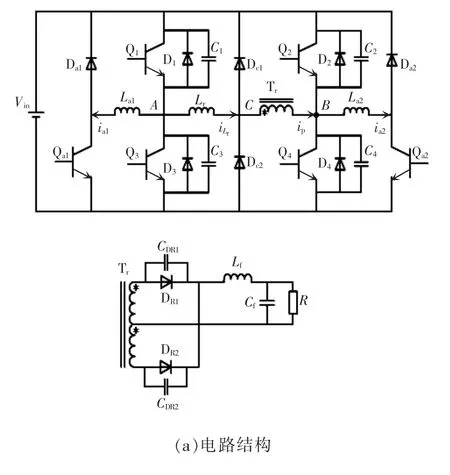
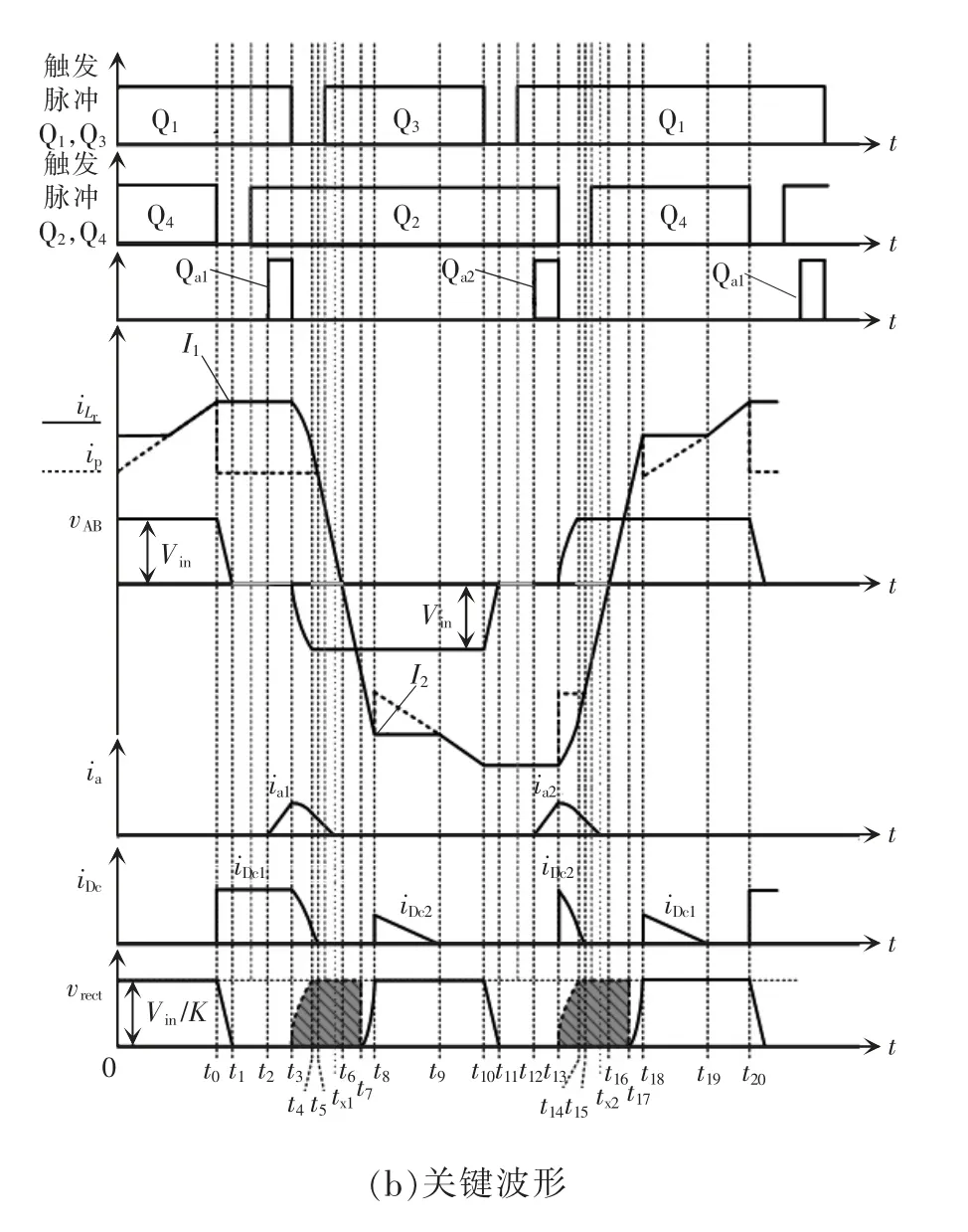
图2 互补占空比调制全桥ZVS变换器电路结构及关键波形Fig.2 Circuit structure and key waveforms of full-bridge ZVS converter based on complementary duty cycle modulation

2 工作原理

在一个开关周期内，该变换器共有20 种工作模态。在分析前，作如下假设：所有开关管、二极管均为理想器件（输出整流二极管等效为一个理想二极管和一个电容并联）；所有电感、电容和变压器均为理想元件；电容C1=C2=C3=C4=Coss，寄生电容CDR1=CDR2=CDR；辅助电感La1=La2=La，输出滤波电感Lf≫Lr/K2，其中，Lr为谐振电感，K为变压器原副边匝比。各开关模态的等效电路如图3 所示。

1）开关模态0（t0时刻前）

在t0时刻前，原边开关管Q1、Q4导通，副边整流二极管DR1导通、DR2截止，原边向副边传递能量。开关模态0 等效电路如图3（a）所示。

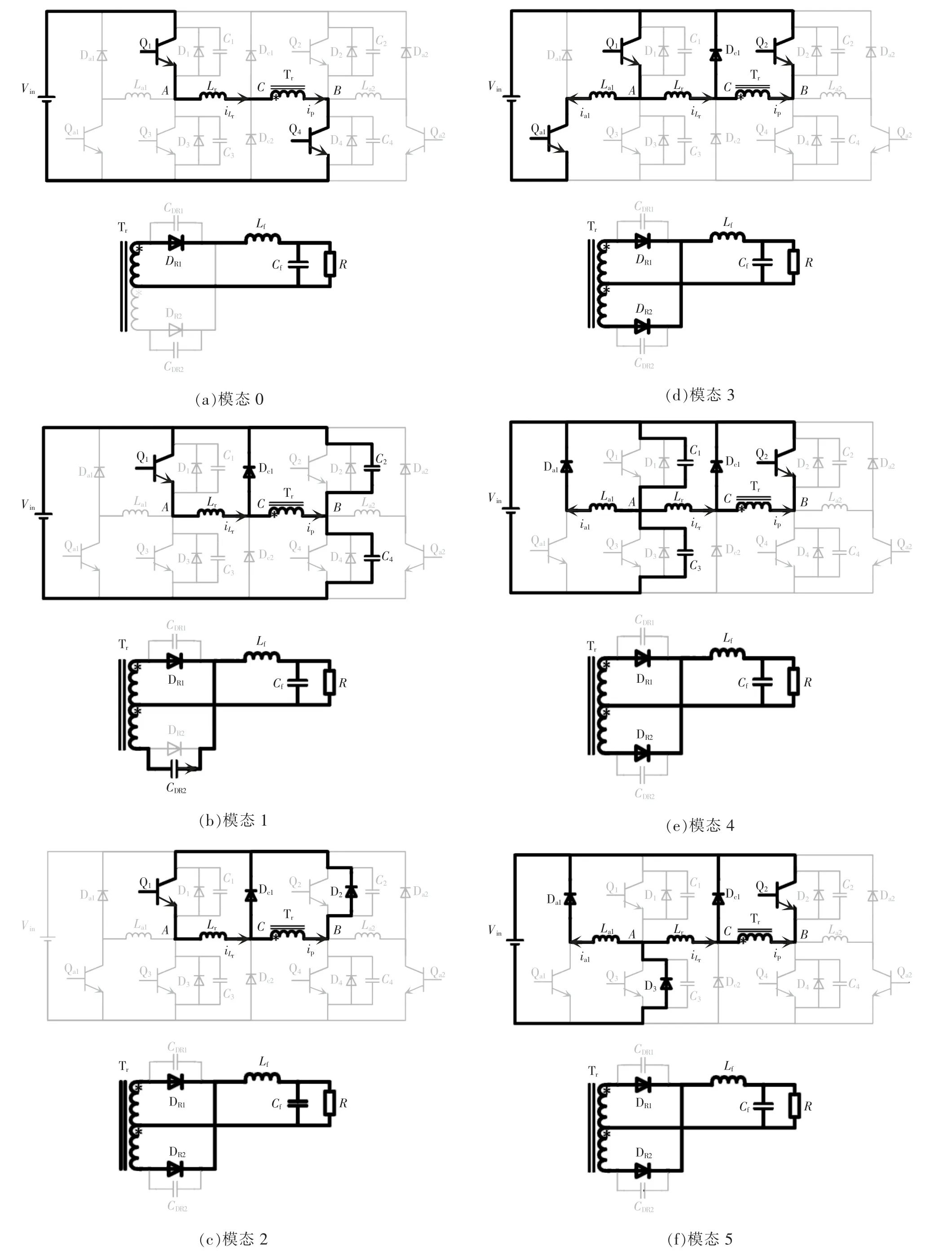
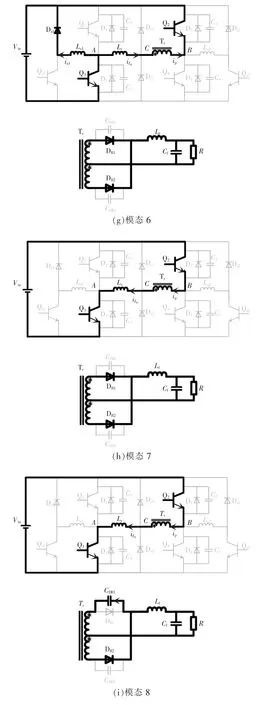
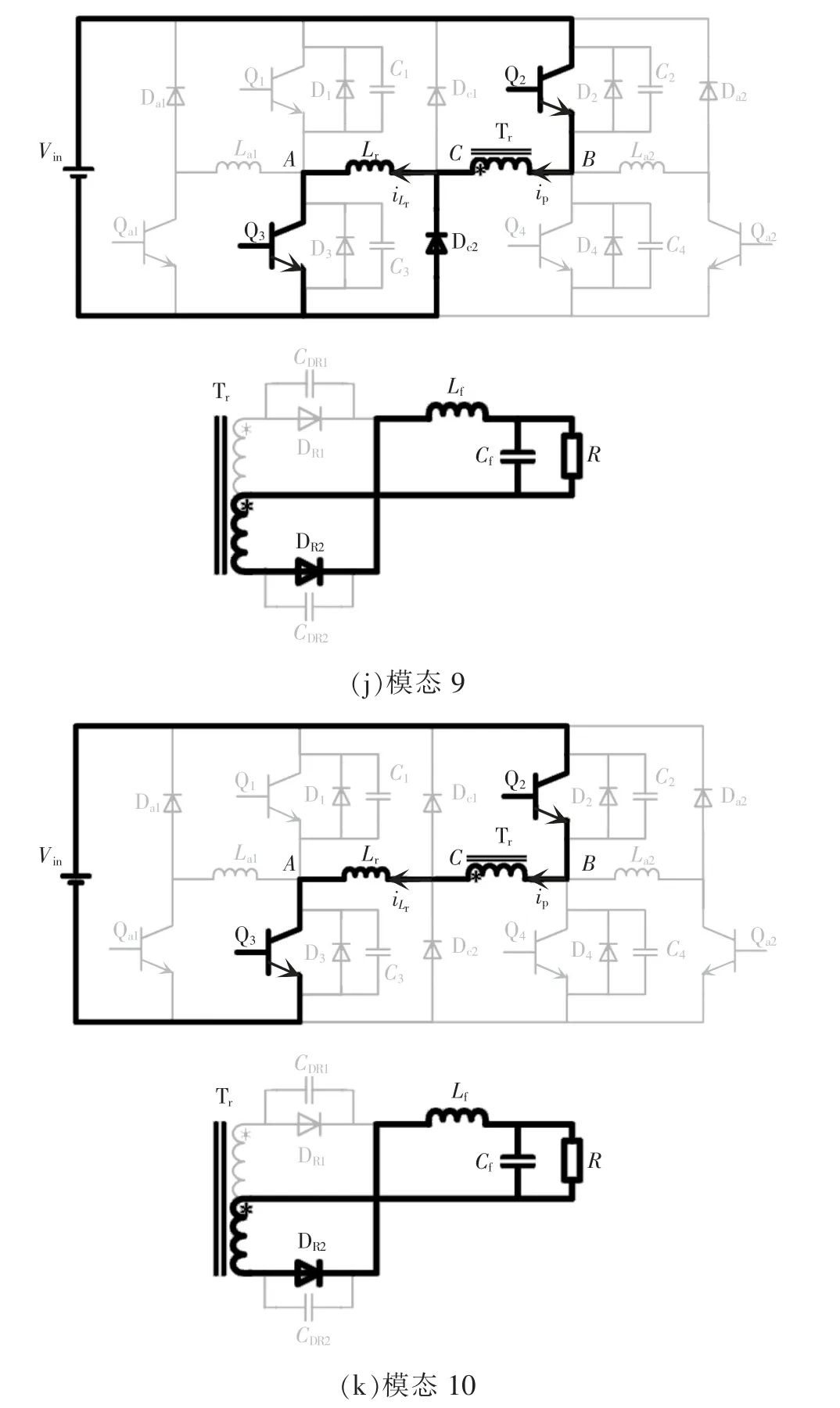
图3 各开关模态的等效电路Fig.3 Equivalent circuit in each switching mode

2）开关模态1（t0～t1时刻）

t0时刻，Q4关断，原边电流ip同时对C4充电和对C2放电，vAB下降。C 点电压随B 点电压的升高而升高，当C 点电压上升至输入电压Vin时，钳位二极管Dc1导通，将C 点电压钳位至Vin。随后变压器原边电压vCB随B 点电压的升高而下降，副边电压也相应下降，输出整流二极管DR2的寄生电容CDR2放电，原边电流ip随之下降。加在谐振电感Lr上的电压vAC=0 和电流保持不变，二者电流差值iDc1流经钳位二极管Dc1。开关模态1 等效电路如图3（b）所示。电容C4、C2的电压和电流、ip分别为

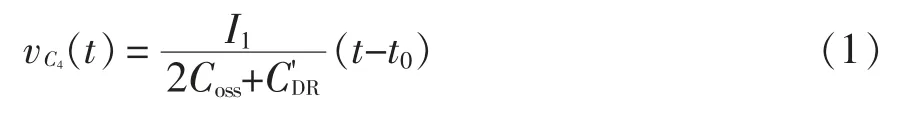
式中：I1为t0时刻原边电流；为整流二极管寄生电容折算至原边的等效值，=4CDR/K2。

3）开关模态2（t1～t2时刻）

t1时刻，C4的电压上升至Vin，C2的电压下降至0，Q2的反并联二极管D2自然导通，此时可以零电压开通Q2；CDR2也同时放电完毕，DR2自然导通。此时DR1和DR2同时导通，均分负载电流。在此开关模态中，vAC=vAB=0，ip和保持不变。开关模态2 等效电路如图3（c）所示。

4）开关模态3（t2～t3）

开关模态3 等效电路如图3（d）所示。t2时刻，开通辅助开关Qa1，辅助电感La1通过Vin→Q1→La1→Qa1→Vin回路进行充电，Vin全部施加在La1上，ia1线性上升，即有

5）开关模态4（t3～t4时刻）

t3时刻，Q1和Qa1关断，辅助电流ia1达到最大值Ia，max。电流ia1和同时对C1充电和对C3放电，此时有vAB=。由于DR1和DR2同时导通，变压器副边和原边电压均为0，即vCB=0，则vAB全部施加在Lr上。此时，Lr和La1同C1和C3谐振工作。开关模态4 等效电路如图3（e）所示。电容C1、C3的电压和电流、ia1的表达式分别为

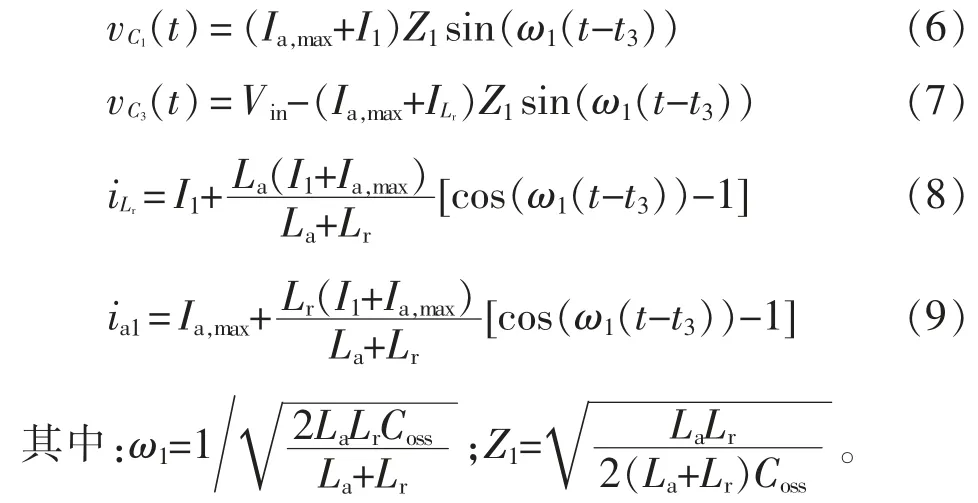
6）开关模态5（t4～t5时刻）

开关模态5 等效电路如图3（f）所示。t4时刻，C1的电压上升至Vin，C3的电压下降至0，Q3的反并联二极管D3自然导通，此时可以零电压开通Q3。Lr与La1均承受反向电压-Vin，与ia1均线性下降，即有

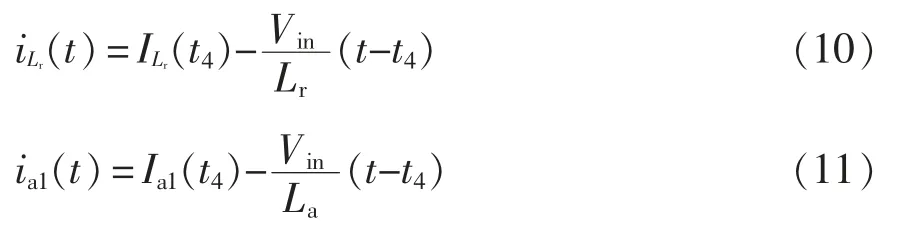
7）开关模态6（t5～t6时刻）

开关模态6 等效电路如图3（g）所示。t5时刻，下降到与ip相等，钳位二极管Dc1自然关断。由于此时ip不足以提供负载电流，DR1和DR2同时导通，vrect=0，vCB=0，vAC=-Vin，iLr与ip同时线性下降，ia1仍保持原斜率变化，直至tx1时刻下降为0，即有

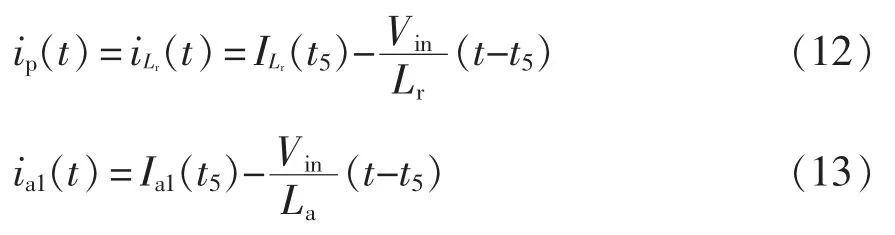
8）开关模态7（t6～时刻t7）

开关模态7 等效电路如图3（h）所示。t6时刻，ip由正值过零且沿负方向增大。由于ip仍不足以提供负载电流，DR1和DR2继续保持同时导通，变压器副边和原边电压均为0，Vin全部反向施加在Lr上，与ip线性下降，即有

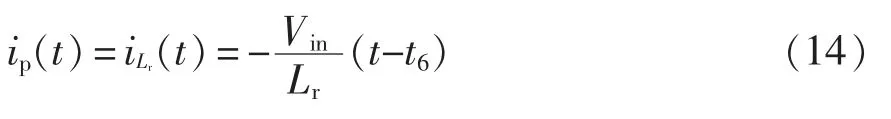
9）开关模态8（t7～t8时刻）

t7时刻，原边电流换向阶段完成，ip达到折算至原边的输出滤波电感电流-ILf（t7）/K，副边整流二极管DR1截止，DR2导通，原边向副边传递能量。在t7之后，Lr同CDR1谐振工作，ip和继续沿负方向增大。开关模态8 等效电路如图3（i）所示。整流二极管寄生电容CDR1的电压和原边电流ip的表达式分别为

10）开关模态9（t8～t9时刻）

开关模态9 等效电路如图3（j）所示。t8时刻，上升至2Vin/K，同时vCB下降至-Vin，此时C 点电压下降至0，钳位二极管Dc2导通，将C 点电压钳位至0。由此vCB被钳位至-Vin，相应地，被钳位至2Vin/K。此时，Ip和分别为

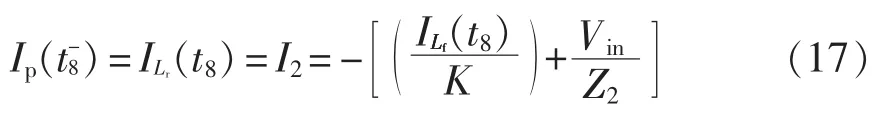
当钳位二极管Dc2导通后，ip阶跃上升到折算至原边的输出滤波电感电流，即，在这段时间内，线性上升，ip也随之沿负方向增大。谐振电感Lr上的电压vAC=0，保持为I2不变，二者差值iDc2流经钳位二极管Dc2。ip的表达式为

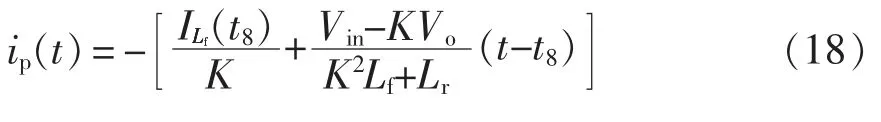
式中，Vo为输出电压幅值。

11）开关模态10（t9～t10时刻）

t9时刻，ip沿负方向增大到与相等，钳位二极管Dc2自然关断。原边开关管Q2、Q3导通，副边整流二极管DR1截止，DR2导通，原边向副边传递能量。开关模态10 等效电路如图3（k）所示。

在t10时刻时，Q3关断，开关模态10 结束，变换器将开始下半周期的工作。由于其下半周工作状态与上半周期类似，仅钳位二极管Dc2的导通时间稍有差异，这里不再赘述。

3 特性分析

3.1 ZVS 范围

由开关模态2 与开关模态5 可知，为实现零电压开通，需要保证在开关管开通之前电路中有足够的能量使其寄生电容两端电压放电为0，使得其反并联二极管能够自然导通，从而将开关管钳位至零电位。

考虑到变压器原边绕组的寄生电容CTR（图中未示出），所提出的变换器实现ZVS，其谐波电感的能量E 应满足

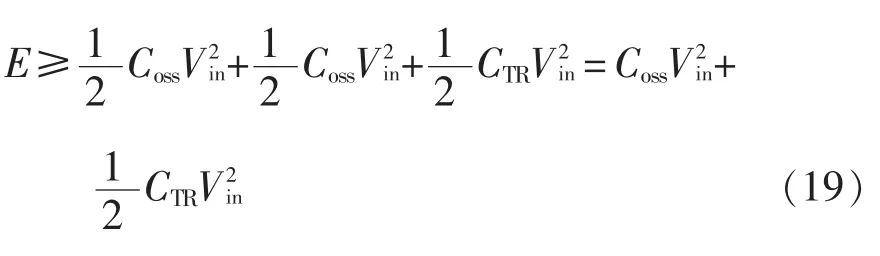
在超前桥臂开关过程中，输出滤波电感Lf与谐振电感Lr串联，如图3（b）所示。开关模态1中，与传统移相全桥变换器工作状态类似，由于Lf足够大，原边电流ip可近似为恒流源，较容易满足

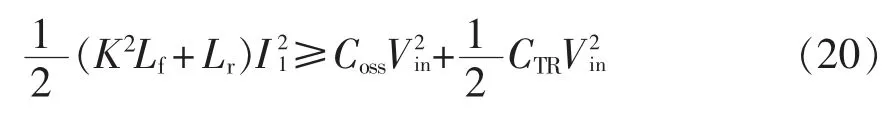
从而实现超前桥臂的ZVS。在滞后桥臂开关过程中，原边电压和原边电流方向相反，副边整流二极管同时导通，使得变压器副边短路，仅有谐振电感参与谐振过程。由于轻载时谐振电感中的能量不足，较难满足

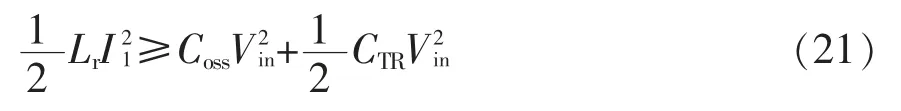
从而丢失滞后桥臂的ZVS。由此，可通过引入如图3（e）所示的辅助并联谐振网络解决该问题。开关模态4中，辅助电感电流与谐振电感电流同时对开关管的寄生电容进行充放电，两者共同提供的能量之和较容易满足

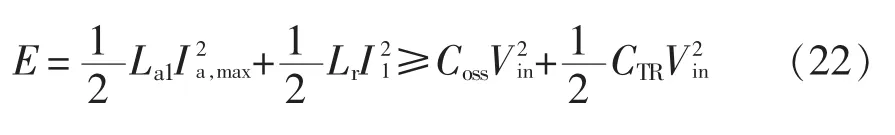
从而保证在轻载条件下仍能实现滞后桥臂的ZVS。在负载较轻时，可以忽略谐振电感提供的能量，因此辅助电流ia1最大值应满足

开关模态3中，辅助开关Qa1开通，辅助电感La1通过输入电压Vin进行充电，辅助电流Ia1线性上升。通过合理设计辅助开关的导通时间，使得辅助电感中储存足够的能量。

联立式（5）和式（23）可得辅助开关Qa1的导通时间t23应满足

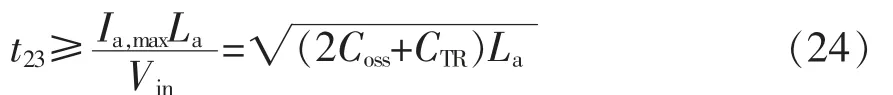
即辅助开关的占空比Da与辅助电感La应满足

式中，Ts为开关周期。

3.2 占空比丢失

从开关模态4 至开关模态7的这一段时间可以看出，由于存在原边电流由正向（或负向）变化到负向（或正向）负载反射电流的换向阶段。在换向阶段内，原边电流不足以提供负载电流，原边存在电压方波而副边短路，导致部分输出电压方波的丢失，继而出现了占空比丢失问题，如图2 中阴影部分所示。

本文所提变换器的占空比丢失可表示为

式中，t37为t3时刻至t7时刻的时间。

由于t3～t4时刻的时间t34很短，可以忽略，且Ip（t7）≈Ip（）=I2，则有

由于引入辅助并联谐振网络可以保证宽范围的ZVS，因此可以考虑选择非常小的谐振电感，缩短所提变换器工作状态中的换向阶段，从而减轻占空比丢失问题，在理论上甚至能够消除占空比丢失，即

3.3 整流侧寄生振荡

在传统移相全桥滞后桥臂的换向阶段完成后，谐振电感Lr同整流二极管寄生电容CDR1谐振工作，由于输入电压Vin的存在，在整流二极管寄生电容的充放电过程中，电容会先充电至一个可达到的最大值，表征为寄生振荡，如图1（b）中虚线方框标记处所示。

开关模态9中，所提出的变换器通过原边钳位二极管在此阶段将变压器钳位，如图3（j）所示，从而消除了寄生振荡问题。

4 仿真分析

为了对比明显，设计了传统移相全桥和所提改进全桥相同的参数：额定功率Po=4.5 kW、输入电压Vin=500 V、输出电压Vo=150 V的。由于在重载条件下，辅助网络可不参与工作，改进全桥的工作状态与传统全桥相似。而在轻载条件下，辅助网络参与工作，两者的工作状态存在明显差异。故本文选在20%负载条件下进行了仿真分析。图4为调制波形，图5 和图6 分别为超前桥臂和滞后桥臂的开关情况。

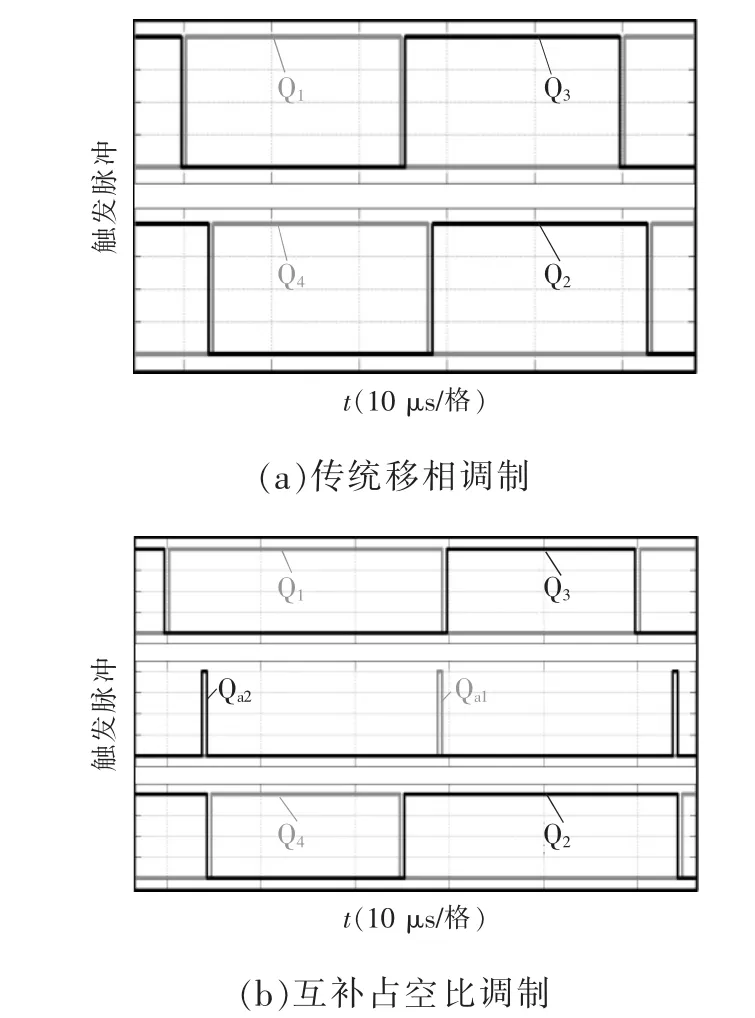
图4 调制波形Fig.4 Modulated waveforms

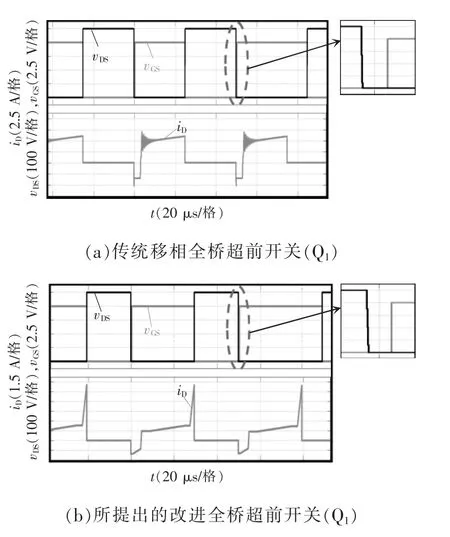
图5 超前桥臂开关情况（20%负载）Fig.5 Condition of leading leg switch（under 20% load）

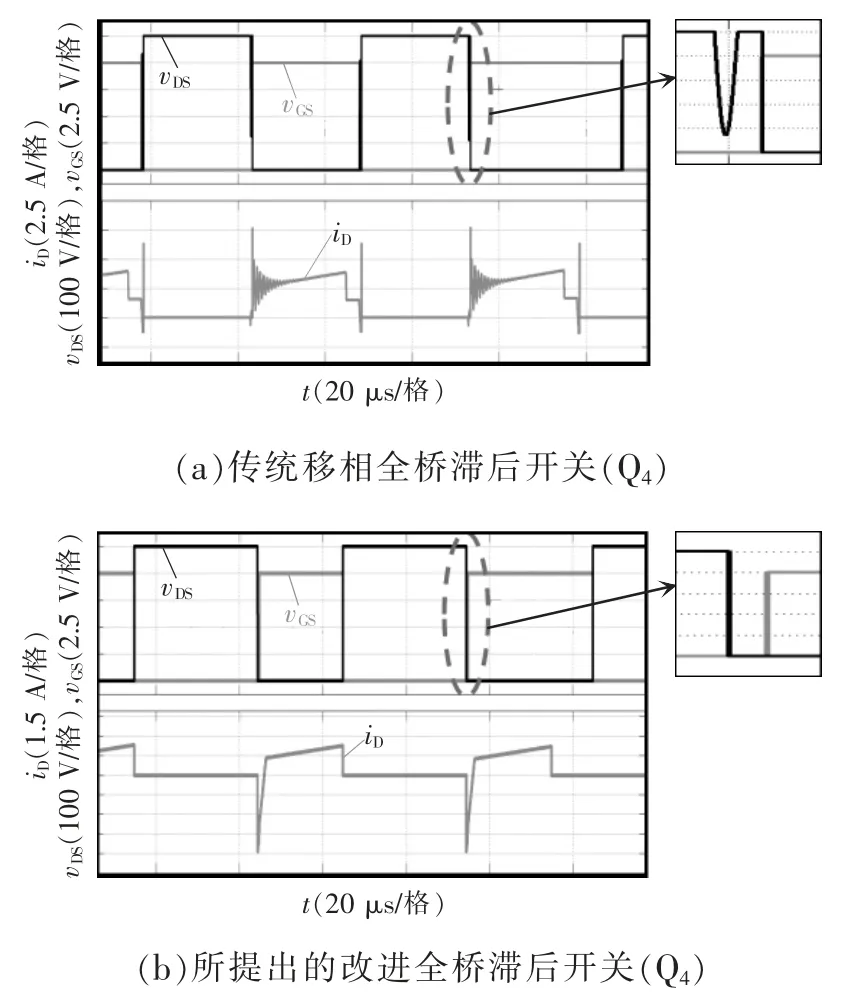
图6 滞后桥臂开关情况（20%负载）Fig.6 Condition of lagging leg switch（under 20% load）

通过仿真波形可以看出，传统移相全桥电路在轻载时滞后桥臂不能实现ZVS，且存在较为严重的寄生振荡问题。所提改进全桥变换器在轻载时仍能实现ZVS，并且消除了寄生振荡问题。

5 结语

本文提出了一种基于互补占空比调制的改进全桥ZVS 直流变换器，通过引入并联辅助谐振网络和原边钳位二极管网络，拓宽了滞后桥臂的软开关范围且消除了整流侧寄生振荡，并在一定程度上大大减轻了占空比丢失问题。在轻载（20%负载）条件下对传统移相全桥和所提出的改进全桥进行了仿真对比，证明了所提改进全桥变换器的优越性，但本文尚未考虑由于引入的原边钳位二极管网络工作状态不对称导致变压器存在直流偏磁问题。为了解决该问题，需要引入消磁手段对直流分量进行抑制，这也是本文有待进一步研究的关键之处。